A Primer on Probabilistic Forecasting

The Smart Forecaster

 Pursuing best practices in demand planning,

forecasting and inventory optimization

If you keep up with the news about supply chain analytics, you are more frequently encountering the phrase “probabilistic forecasting.” If this phrase is puzzling, read on.

You probably already know what “forecasting” means. And you probably also know that there seem to be lots of different ways to do it. And you’ve probably heard pungent little phrases like “every forecast is wrong.” So you know that some kind of mathemagic might calculate that “the forecast is you will sell 100 units next month”, and then you might sell 110 units, in which case you have a 10% forecast error.

You may not know that what I just described is a particular kind of forecast called a “point forecast.” A point forecast is so named because it consists of just a single number (i.e., one point on the number line, if you recall the number line from your youth).

Point forecasts have one virtue: They are simple. They also have a flaw: They give rise to snarky statements like “every forecast is wrong.” That is, in most realistic cases, it is unlikely that the actual value will exactly equal the forecast. (Which isn’t such a big deal if the forecast is close enough.)

This gets us to “probabilistic forecasting.” This approach is a step up, because instead of producing a single-number (point) forecast, it yields a probability distribution for the forecast. And unlike traditional extrapolative models that rely purely on the historical data, probabilistic forecasts have the ability to simulate future values that aren’t anchored to the past.

“Probability distribution” is a forbidding phrase, evoking some arcane math that you may have heard of but never studied. Luckily, most adults have enough life experience to have an intuitive grasp of the concept.  When broken down, it’s quite straightforward to understand.

Imagine the simple act of flipping two coins. You might call this harmless fun, but I call it a “probabilistic experiment.” The total number of heads that turn up on the two coins will be either zero, one or two. Flipping two coins is a “random experiment.” The resulting number of heads is a “random variable.” It has a “probability distribution”, which is nothing more than a table of how likely it is that the random variable will turn out to have any of its possible values. The probability of getting two heads when the coins are fair works out to be ¼, as is the probability of no heads. The chance of one head is ½.

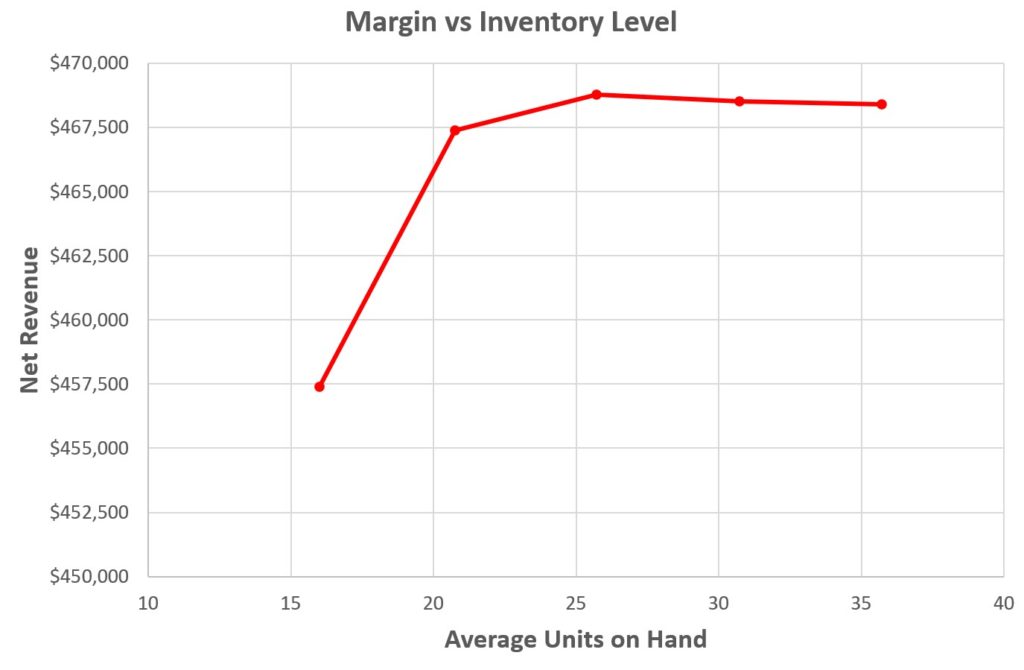
The same approach can describe a more interesting random variable, like the daily demand for a spare part.  Figure 2 shows such a probability distribution. It was computed by compiling three years of daily demand data on a certain part used in a scientific instrument sold to hospitals.

 

Probabilistic demand forecast 1

Figure 1: The probability distribution of daily demand for a certain spare part

 

The distribution in Figure 1 can be thought of as a probabilistic forecast of demand in a single day. For this particular part, we see that the forecast is very likely to be zero (97% chance), but sometimes will be for a handful of units, and once in three years will be twenty units. Even though the most likely forecast is zero, you would want to keep a few on hand if this part were critical (“…for want of a nail…”)

Now let’s use this information to make a more complicated probabilistic forecast. Suppose you have three units on hand. How many days will it take for you to have none? There are many possible answers, ranging from a single day (if you immediately get a demand for three or more) up to a very large number (since 97% of days see no demand).  The analysis of this question is a bit complicated because of all the many ways this situation can play out, but the final answer that is most informative will be a probability distribution. It turns out that the number of days until there are no units left in stock has the distribution shown in Figure 2.

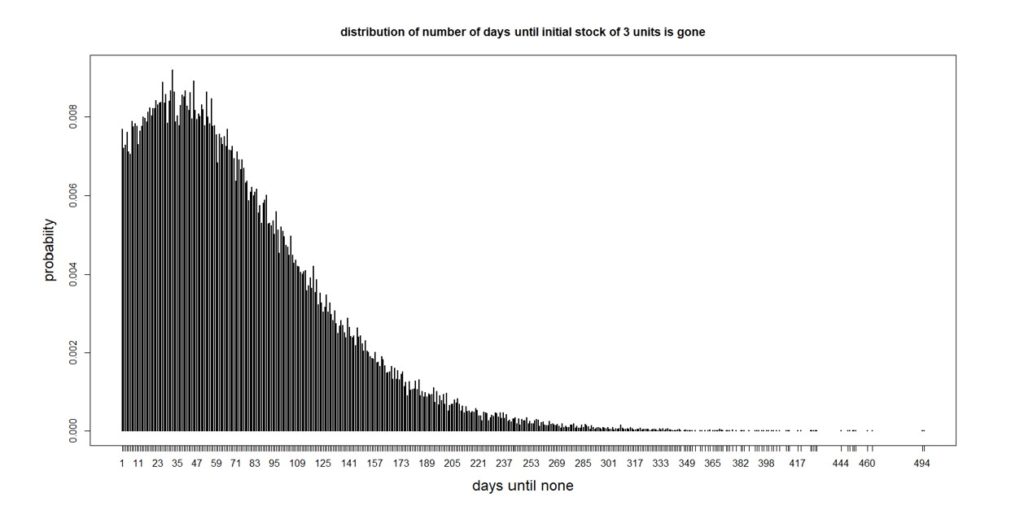
Probabilistic demand forecast 2

Figure 2: Distribution of the number of days until all three units are gone

 

The average number of days is 74, which would be a point forecast, but there is a lot of variation around the average. From the perspective of inventory management, it is notable that there is a 25% chance that all the units will be gone after 32 days. So if you decided to order more when you were down to only three on the shelf, it would be good to have the supplier get them to you before a month has passed. If they couldn’t, you’d have a 75% chance of stocking out – not good for a critical part.

The analysis behind Figure 2 involved making some assumptions that were convenient but not necessary if they were not true. The results came from a method called “Monte Carlo simulation”, in which we start with three units, pick a random demand from the distribution in Figure 1, subtract it from the current stock, and continue until the stock is gone, recording how many days went by before you ran out. Repeating this process 100,000 times produced Figure 2.

Applications of Monte Carlo simulation extend to problems of even larger scope than the “when do we run out” example above. Especially important are Monte Carlo forecasts of future demand. While the usual forecasting result is a set of point forecasts (e.g., expected unit demand over the next twelve months), we know that there are any number of ways that the actual demand could play out. Simulation could be used to produce, say, one thousand possible sets of 365 daily demand demands.

This set of demand scenarios would more fully expose the range of possible situations with which an inventory system would have to cope. This use of simulation is called “stress testing”, because it exposes a system to a range of varied but realistic scenarios, including some nasty ones. Those scenarios are then input to mathematical models of the system to see how well it will cope, as reflected in key performance indicators (KPI’s). For instance, in those thousand simulated years of operation, how many stockouts are there in the worst year? the average year? the best year? In fact, what is the full probability distribution of the number of stockouts in a year, and what is the distribution of their size?

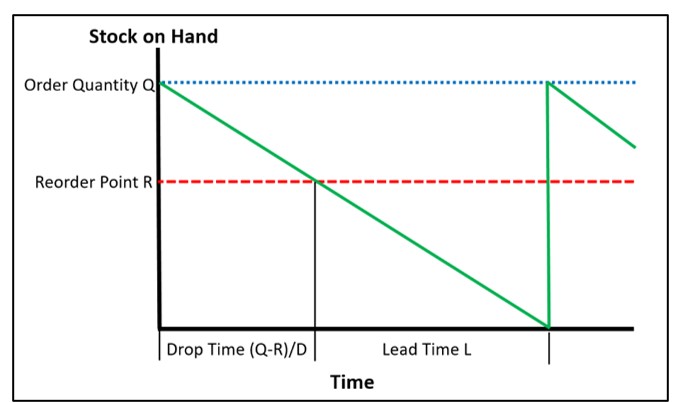
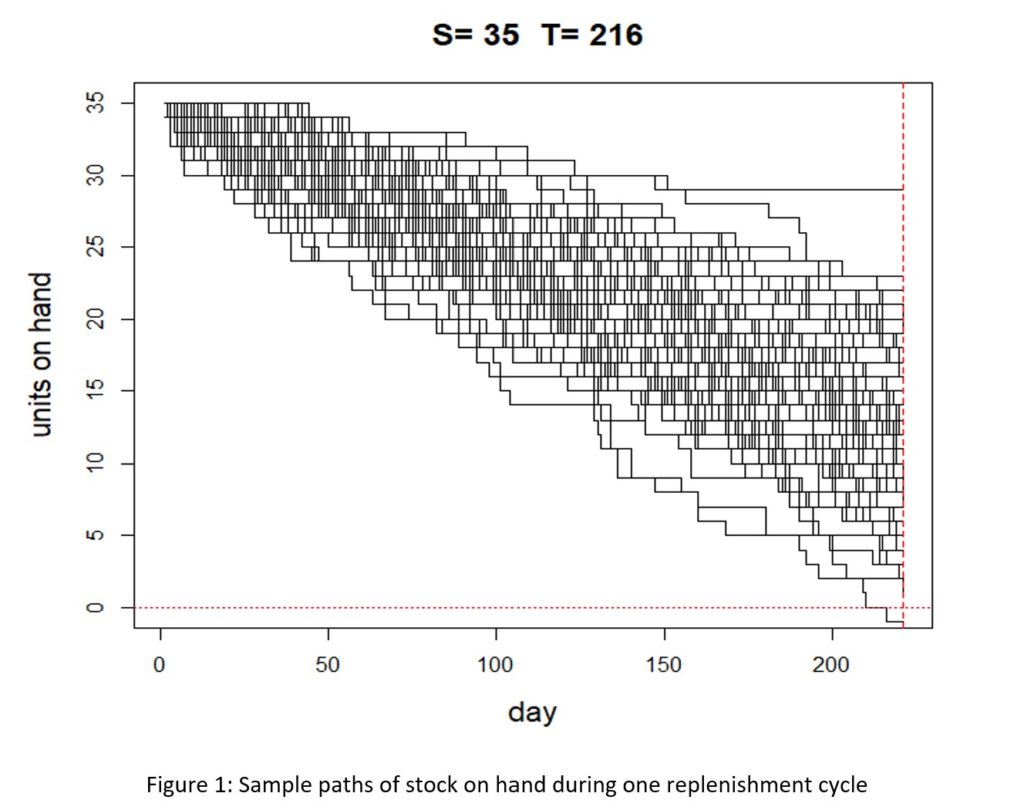
Figures 3 and 4 illustrate probabilistic modeling of an inventory control system that converts stockouts to backorders. The system simulated uses a Min/Max control policy with Min = 10 units and Max = 20 units.

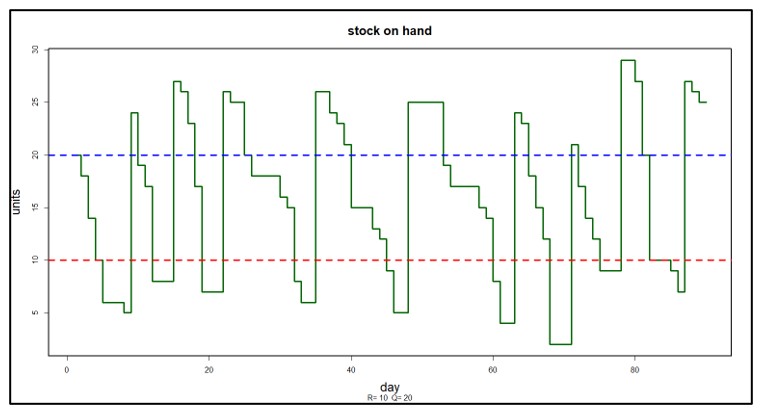
Figure 3 shows one simulated year of daily operations in four plots. The first plot shows a particular pattern of random daily demand in which average demand increases steadily from Monday to Friday but disappears on weekends. The second plot shows the number of units on hand each day. Note that there are a dozen times during this simulated year when inventory goes negative, indicating stockouts. The third plot shows the size and timing of replenishment orders. The fourth plot shows the size and timing of backorders.  The information in these plots can be translated into estimates of inventory investment, average units on hand, holding costs, ordering costs and shortage costs.

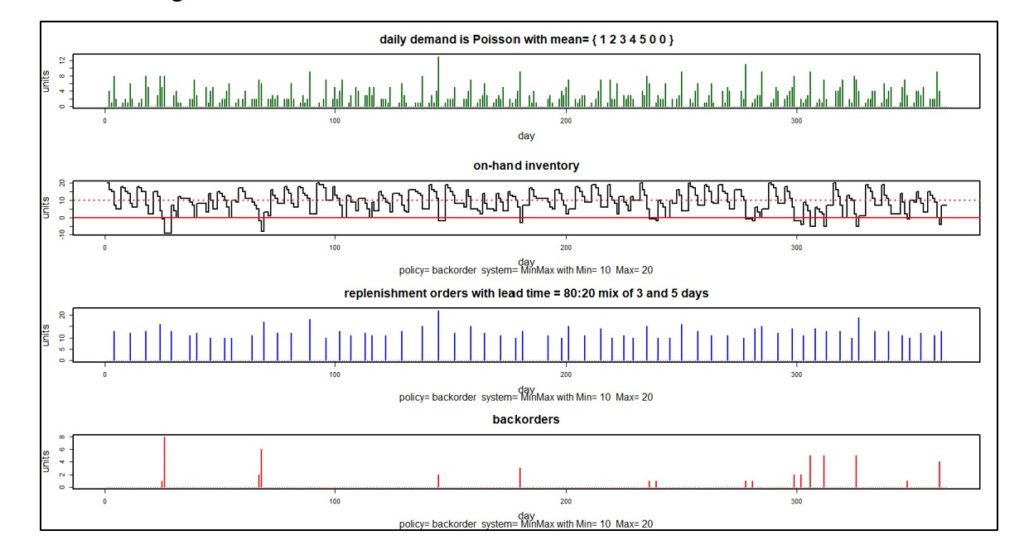
Probabilistic demand forecast 3

Figure 3: One simulated year of inventory system operation

 

Figure 3 shows one of one thousand simulated years. Each year will have different daily demands, resulting in different values of metrics like units on hand and the various components of operating cost. Figure 4 plots the distribution of 1,000 simulated values of four KPI’s. Simulating 1,000 years of imagined operation exposes the range of possible results so that planners can account not just for average results but also see best-case and worst-case values.

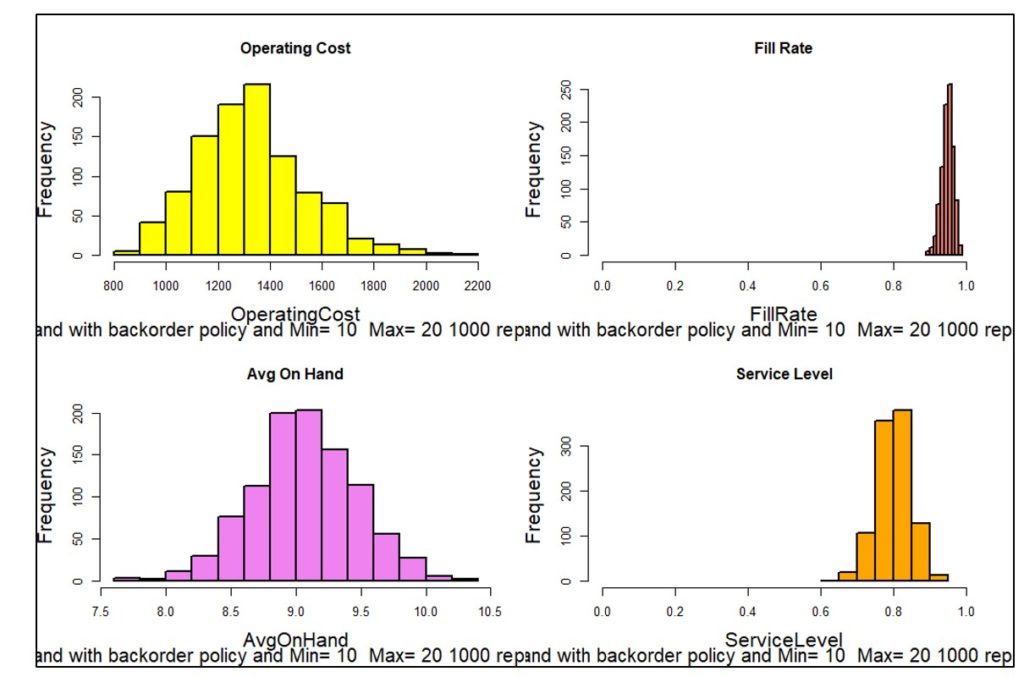
Probabilistic demand forecast 4

Figure 4: Distributions of four KPI’s based on 1,000 simulations

 

Monte Carlo simulation is a low-math/high-results approach to probabilistic forecasting: very practical and easy to explain. Advanced probabilistic forecasting methods employed by Smart Software expand upon standard Monte Carlo simulation, yielding extremely accurate estimates of required inventory levels.

 

Leave a Comment

Related Posts

Call an Audible to Proactively Counter Supply Chain Noise

Call an Audible to Proactively Counter Supply Chain Noise

You know the situation: You work out the best way to manage each inventory item by computing the proper reorder points and replenishment targets, then average demand increases or decreases, or demand volatility changes, or suppliers’ lead times change, or your own costs change.

Recent Posts

  • Top Five Tips for New Demand Planners and ForecastersTop Five Tips for New Demand Planners and Forecasters
    Good forecasting can make a big difference to your company’s performance, whether you are forecasting to support sales, marketing, production, inventory, or finance. This blog is aimed primarily at those fortunate individuals who are about to start this adventure. Welcome to the field! […]
  • Dynamics Community Summit eventSmart Software to Present at Community Summit North America
    Smart Software's Channel Sales Director and Enterprise Solution Engineer, to present three sessions at this year’s Microsoft Dynamics Community Summit North America event in Orlando, FL. . […]

    Goldilocks Inventory Levels

    You may remember the story of Goldilocks from your long-ago youth. Sometimes the porridge was too hot, sometimes it was too cold, but just once it was just right. Now that we are adults, we can translate that fairy tale into a professional principle for inventory planning: There can be too little or too much inventory, and there is some Goldilocks level that is “just right.” This blog is about finding that sweet spot.

    To illustrate our supply chain fable, consider this example. Imagine that you sell service parts to keep your customers systems up and running. You offer a particular service part that costs you $100 to make but sells for a 20% markup. You can make $20 on each unit you sell, but you don’t get to keep the whole $20 because of the inventory operating costs you bear to be able to sell the part. There are holding costs to keep the part in good repair while in stock and ordering costs to replenish units you sell. Finally, sometimes you lose revenue from lost sales due to stockouts.  

    These operating costs can be directly related to the way you manage the part in inventory. For our example, assume you use a (Q,R) inventory policy, where Q is the replenishment order quantity and R is the reorder point. Assume further that the reason you are not making $30 per unit is that you have competitors, and customers will get the part from them if they can’t get it from you.

    Both your revenue and your costs depend in complex ways on your choices for Q and R. These will determine how much you order, when and therefore how often you order, how often you stock out and therefore how many sales you lose, and how much cash you tie up in inventory. It is impossible to cost out these relationships by guesswork, but modern software can make the relationships visible and calculate the dollar figures you need to guide your choice of values for Q and R. It does this by running detailed, fact-based, probabilistic simulations that predict costs and performance by averaging over a large number of realistic demand scenarios.  

    With these results in hand, you can work out the margin associated with (Q,R) values using the simple formula

    Margin = (Demand – Lost Sales) x Profit per unit sold – Ordering Costs – Holding Costs.

    In this formula, Lost Sales, Ordering Costs and Holding Costs are dependent on reorder point R and order quantity Q.

    Figure 1 shows the result of simulations that fixed Q at 25 units and varied R from 10 to 30 in steps of 5. While the curve is rather flat on top, you would make the most money by keeping on-hand inventory around 25 units (which corresponds to setting R = 20). More inventory, despite a higher service level and fewer lost sales, would make a little less money (and ties up a lot more cash), and less inventory would make a lot less.

     

    Margins vs Inventory Level Business

    Figure 1: Showing that there can be too little or too much inventory on hand

     

    Without relying on the inventory simulation software, we would not be able to discover

    • a) that it is possible to carry too little and too much inventory
    • b) what the best level of inventory is
    • c) how to get there by proper choices of reorder point R and order quantity Q.

     

    Without an explicit understanding of the above, companies will make daily inventory decisions relying on gut feel and averaging based rule of thumb methods. The tradeoffs described here are not exposed and the resulting mix of inventory yields a far lower return forfeiting hundreds of thousands to millions per year in lost profits.  So be like Goldilocks.  With the right systems and software tools, you too can get it just right!    

     

     

    Leave a Comment
    Related Posts
    Top Five Tips for New Demand Planners and Forecasters

    Top Five Tips for New Demand Planners and Forecasters

    Good forecasting can make a big difference to your company’s performance, whether you are forecasting to support sales, marketing, production, inventory, or finance. This blog is aimed primarily at those fortunate individuals who are about to start this adventure. Welcome to the field!

    Probabilistic vs. Deterministic Order Planning

    The Smart Forecaster

    Man with a computer in a warehouse best practices in demand planning, forecasting and inventory optimization

    Consider the problem of replenishing inventory. To be specific, suppose the inventory item in question is a spare part. Both you and your supplier will want some sense of how much you will be ordering and when. And your ERP system may be insisting that you let it in on the secret too.

    Deterministic Model of Replenishment

    The simplest way to get a decent answer to this question is to assume the world is, well, simple. In this case, simple means “not random” or, in geek speak, “deterministic.” In particular, you pretend that the random size and timing of demand is really a continuous drip-drip-drip of a fixed size coming at a fixed interval, e.g., 2, 2, 2, 2, 2, 2… If this seems unrealistic, it is. Real demand might look more like this: 0, 1, 10, 0, 1, 0, 0, 0 with lots of zeros, occasional but random spikes.

    But simplicity has its virtues. If you pretend that the average demand occurs every day like clockwork, it is easy to work out when you will need to place your next order, and how many units you will need.  For instance, suppose your inventory policy is of the (Q,R) type, where Q is a fixed order quantity and R is a fixed reorder point. When stock drops to or below the reorder point R, you order Q units more. To round out the fantasy, assume that the replenishment lead time is also fixed: after L days, those Q new units will be on the shelf ready to satisfy demand.

    All you need now to answer your questions is the average demand per day D for the item. The logic goes like this:

    1. You start each replenishment cycle with Q units on hand.
    2. You deplete that stock by D units per day.
    3. So, you hit the reorder point R after (Q-R)/D days.
    4. So, you order every (Q-R)/D days.
    5. Each replenishment cycle lasts (Q-R)/D + L days, so you make a total of 365D/(Q-R+LD) orders per year.
    6. As long as lead time L < R/D, you will never stock out and your inventory will be as small as possible.

    Figure 1 shows the plot of on-hand inventory vs time for the deterministic model. Around Smart Software, we refer to this plot as the “Deterministic Sawtooth.” The stock starts at the level of the last order quantity Q. After steadily decreasing over the drop time (Q-R)/D, the level hits the reorder point R and triggers an order for another Q units. Over the lead time L, the stock drops to exactly zero, then the reorder magically arrives and the next cycle begins.

    Figure 1 Deterministic model of on-hand inventory

    Figure 1: Deterministic model of on-hand inventory

     

    This model has two things going for it. It requires no more than high school algebra, and it combines (almost) all the relevant factors to answer the two related questions: When will we have to place the next order? How many orders will we place in a year?

    Probabilistic Model of Replenishment

    Not surprisingly, if we strip away some of the fantasy from the deterministic model, we get more useful information. The probabilistic model incorporates all the messy randomness in the real-world problem: the uncertainty in both the timing and size of demand, the variation in replenishment lead time, and the consequences of those two factors: the chance of stock on hand undershooting the reorder point, the chance that there will be a stockout, the variability in the time until the next order, and the variable number of orders executed in a year.

    The probabilistic model works by simulating the consequences of uncertain demand and variable lead time. By analyzing the item’s historical demand patterns (and excluding any observations that were recorded during a time when demand may have been fundamentally different), advanced statistical methods create an unlimited number of realistic demand scenarios. Similar analysis is applied to records of supplier lead times. Combining these supply and demand scenarios with the operational rules of any given inventory control policy produces scenarios of the number of parts on hand. From these scenarios, we can extract summaries of the varying intervals between orders.

    Figure 2 shows an example of a probabilistic scenario; demand is random, and the item is managed using reorder point R = 10 and order quantity Q=20. Gone is the Deterministic Sawtooth; in its place is something more complex and realistic (the Probabilistic Staircase). During the 90 simulated days of operation, there were 9 orders placed, and the time between orders clearly varied.

    Using the probabilistic model, the answers to the two questions (how long between orders and how many in a year) get expressed as probability distributions reflecting the relative likelihoods of various scenarios. Figure 3 shows the distribution of the number of days between orders after ten years of simulated operation. While the average is about 8 days, the actual number varies widely, from 2 to 17.

    Instead of telling your supplier that you will place X orders next year, you can now project X ± Y orders, and your supplier knows better their upside and downside risks. Better yet, you could provide the entire distribution as the richest possible answer.

    Figure 2 A probabilistic scenario of on-hand inventory

    Figure 2 A probabilistic scenario of on-hand inventory

     

    Figure 3 Distribution of days between orders

    Figure 3: Distribution of days between orders

     

    Climbing the Random Staircase to Greater Efficiency

    Moving beyond the deterministic model of  inventory opens up new possibilities for optimizing operations. First, the probabilistic model allows realistic assessment of stockout risk. The simple model in Figure 1 implies there is never a stockout, whereas probabilistic scenarios allow for the possibility (though in Figure 2 there was only one close call around day 70). Once the risk is known, software can optimize by searching  the “design space” (i.e., all possible values of R and Q) to find a design that meets a target level of stockout risk at minimal cost. The value of the deterministic model in this more realistic analysis is that it provides a good starting point for the search through design space.

    Summary

    Modern software provides answers to operational questions with various degrees of detail. Using the example of the time between replenishment orders, we’ve shown that the answer can be calculated approximately but quickly by a simple deterministic model. But it can also be provided in much richer detail with all the variability exposed by a probabilistic model. We think of these alternatives as complementary. The deterministic model bundles all the key variables into an easy-to-understand form. The probabilistic model provides additional realism that professionals expect and supports effective search for optimal choices of reorder point and order quantity.

     

    Leave a Comment
    Related Posts
    Top Five Tips for New Demand Planners and Forecasters

    Top Five Tips for New Demand Planners and Forecasters

    Good forecasting can make a big difference to your company’s performance, whether you are forecasting to support sales, marketing, production, inventory, or finance. This blog is aimed primarily at those fortunate individuals who are about to start this adventure. Welcome to the field!

    Increasing Revenue by Increasing Spare Part Availability

    The Smart Forecaster

     Pursuing best practices in demand planning,

    forecasting and inventory optimization

    Let’s start by recognizing that increased revenue is a good thing for you, and that increasing the availability of the spare parts you provide is a good thing for your customers.

    But let’s also recognize that increasing item availability will not necessarily lead to increased revenue. If you plan incorrectly and end up carrying excess inventory, the net effect may be good for your customers but will definitely be bad for you. There must be some right way to make this a win-win, if only it can be recognized.

    To make the right decision here, you have to think systematically about the problem. That requires that you use probabilistic models of the inventory control process.

     

    A Scenario

    Let’s consider a specific, realistic scenario. Quite a number of factors have an influence on the results:

    • The item: A specific low-volume spare part.
    • Demand mean: Averaging 0.1 units per day (so, highly “intermittent”)
    • Demand standard deviation: 0.35 units per day (so, highly variable or “overdispersed”).
    • Supplier average lead time: 5 days.
    • Unit cost: $100.
    • Holding cost per year as % of unit cost: 10%.
    • Ordering cost per PO cut: $25.
    • Stockout consequences: Lost sales (so, a competitive market, no backorders).
    • Shortage cost per lost sale: $100.
    • Service level target: 85% (so, 15% chance of a stockout in any replenishment cycle).
    • Inventory control policy: Periodic-review/Order-up-to (also called at (T,S) policy)

     

    Inventory Control Policy

    A word about the inventory control policy. The (T,S) policy is one of several that are common in practice. Though there are other more efficient policies (e.g., they don’t wait for T days to go by before making adjustment to stock), (T,S) is one of the simplest and so it is quite popular. It works this way: Every T days, you check how many units you have in stock, say X units. Then you order S-X units, which appear after the supplier lead time (in this case, 5 days). The T in (T,S) is the “order interval”, the number of days between orders; the S is the “order-up-to level”, the number of units you want to have on hand at the start of each replenishment cycle.

    To get the most out of this policy, you must wisely pick values of T and S. Picking wisely means you cannot win by guessing or using simple rule-of-thumb guides like “Keep an average of 3 x average demand on hand.”  Poor choices of T and S hurt both your customers and your bottom line. And sticking too long with choices that were once good can result in poor performance should any of the factors above change significantly, so the values of T and S should be recalculated now and then.

    The smart way to pick the right values of T and S is to use probabilistic models encoded in advanced software. Using software is essential when you have to scale up and pick values of T and S that are right for not one item but hundreds or thousands.

     

    Analysis of Scenario

    Let’s think about how to make money in this scenario. What’s the upside? If there were no expenses, this item could generate an average of $3,650 per year: 0.1 units/day x 365 days x $100/unit. Subtracted from that will be operating costs, comprised of holding, ordering and shortage costs. Each of those will depend on your choices of T and S.

    The software provides specific numbers: Setting T = 321 days and S = 40 units will result in average annual operating costs of $604, giving an expected margin of $3,650 – $604 = $3,046. See Table 1, left column. This use of software is called “predictive analytics” because it translates system design inputs into estimates of a key performance indicator, margin.

    Now think about whether you can do better. The service level target in this scenario is 85%, which is a somewhat relaxed standard that is not going to turn any heads. What if you could offer your customers a 99% service level? That sounds like a distinct competitive advantage, but would it reduce your margin? Not if you properly adjust the values of T and S.

    Setting T = 216 days and S = 35 units will reduce average annual operating costs to $551 and increase expected margin to $3,650 – $551 = $3,099. See Table 1, right column. Here is the win-win we wanted: higher customer satisfaction and roughly 2% more revenue. This use of the software is called “sensitivity analysis” because it shows how sensitive the margin is to the choice of service level target.

    Software can also help you visualize the complex, random dynamics of inventory movements. A by-product of the analysis that populated Table 1 are graphs showing the random paths taken by stock as it decreases over a replenishment cycle. Figure 1 shows a selection of 100 random scenarios for the scenario in which the service level target is 99%. In the figure, only 1 of the 100 scenarios resulted in a stockout, confirming the accuracy of the choice of order-up-to-level.

     

    Summary

    Management of spare parts inventories is often done haphazardly using gut instinct, habit, or obsolete rule-of-thumb. Winging it this way is not a reliable and reproducible path to higher margin or higher customer satisfaction. Probability theory, distilled into probability models then encoded in advanced software, is the basis for coherent, efficient guidance about how to manage spare parts based on facts: demand characteristics, lead times, service level targets, costs and the other factors. The scenarios analyzed here illustrate that it is possible to achieve both higher service levels and higher margin. A multitude of scenarios not shown here offer ways to achieve higher service levels but lose margin. Use the software.

    Scenarios with different service level targets

    Stock on hand during one replenishment cycle

     

     

    Leave a Comment

    Related Posts

    Call an Audible to Proactively Counter Supply Chain Noise

    Call an Audible to Proactively Counter Supply Chain Noise

    You know the situation: You work out the best way to manage each inventory item by computing the proper reorder points and replenishment targets, then average demand increases or decreases, or demand volatility changes, or suppliers’ lead times change, or your own costs change.

    Recent Posts

    • Top Five Tips for New Demand Planners and ForecastersTop Five Tips for New Demand Planners and Forecasters
      Good forecasting can make a big difference to your company’s performance, whether you are forecasting to support sales, marketing, production, inventory, or finance. This blog is aimed primarily at those fortunate individuals who are about to start this adventure. Welcome to the field! […]
    • Dynamics Community Summit eventSmart Software to Present at Community Summit North America
      Smart Software's Channel Sales Director and Enterprise Solution Engineer, to present three sessions at this year’s Microsoft Dynamics Community Summit North America event in Orlando, FL. . […]

      Coping with Surging Demand During the Rebound

      The Smart Forecaster

       Pursuing best practices in demand planning,

      forecasting and inventory optimization

      Many of our customers that saw demand dry up during the pandemic are now seeing demand return.  Some are seeing a significant demand surge. Other customers in critical industries like plastics, biotech, semiconductors and electronics saw demand surges starting as far back as last April. For suggestions about how to cope with these situations, please read on.

      Surging demand usually creates two problems: inability to fill orders and inability to get replenishment due to supplier overload. This situation requires changes in the way you use your advanced planning software. Here are three tips to help you cope.

       

      Tip #1: Narrow your temporal focus

       

      In normal times (remember those?), more data implied better results. Nowadays, old data poison your calculations, since they represent conditions that no longer apply. You should base forecasts and other calculations on data from the current situation. Where to cut off past data may be obvious from a plot of the data, or you may decide to set a “reasonable” cutoff date based on a consensus of colleagues.  Smart Software has developed machine learning algorithms that automatically identify how much historical data should be optimally fed to the forecast model. Be on the lookout for these enhancements to the software that will be rolling out soon. In the meantime, conduct accuracy tests using held-out actuals using different historical start dates.  Smart’s forecast vs. actual feature will support this automatically.

      Smart Demand Planner forecasts vs. actual report

       

      Tip #2: Increase your planning tempo

       

      When operations are stable, you can set your inventory policies and trust them to be appropriate for a long time. When times are turbulent, it is important to increase the frequency of your planning cycles to keep old policy settings from drifting too far away from optimality.  More frequent recalibration of your stocking policies and forecasts means that you’ll be quicker to catch trends that will surprise your competition and always keep you steps ahead.  With software capable of automatically selecting optimal values, all that work can be done in one shot by the software. You should review those changes and possibly tweak them, but it makes sense to let the software do the bulk of the work.

       

      Tip #3: Do more What-If planning

       

      In turbulent times, you might expect even more turbulence in the future. Using your software for what-if planning helps you prepare for changes that may be coming. For example, suppose you’ve been in touch with a key supplier who hints that they may be raising prices or may have to slip their delivery schedules. By feeding the software different inputs, you can do contingency planning. If prices go up, you can see how responding by changing order quantities would impact your inventory operating costs and inventory investment. If lead times go up, you can see what the impact would be on item availability. This foreknowledge helps you figure out what your counter-moves would be before the crisis hits.

      If there ever was a time when we could cruise on automatic pilot, it’s in the rear-view mirror. Your organization, coping with explosive growth, has many challenges. Old answers are obsolete; new answers have to come from somewhere, fast. Advanced software that leverages probabilistic forecasting can help, along with changes in planning processes.

       

      Leave a Comment

      Related Posts

      Call an Audible to Proactively Counter Supply Chain Noise

      Call an Audible to Proactively Counter Supply Chain Noise

      You know the situation: You work out the best way to manage each inventory item by computing the proper reorder points and replenishment targets, then average demand increases or decreases, or demand volatility changes, or suppliers’ lead times change, or your own costs change.

      Recent Posts

      • Top Five Tips for New Demand Planners and ForecastersTop Five Tips for New Demand Planners and Forecasters
        Good forecasting can make a big difference to your company’s performance, whether you are forecasting to support sales, marketing, production, inventory, or finance. This blog is aimed primarily at those fortunate individuals who are about to start this adventure. Welcome to the field! […]
      • Dynamics Community Summit eventSmart Software to Present at Community Summit North America
        Smart Software's Channel Sales Director and Enterprise Solution Engineer, to present three sessions at this year’s Microsoft Dynamics Community Summit North America event in Orlando, FL. . […]