In my previous post in this series on essential concepts, “What is ‘A Good Forecast’”, I discussed the basic effort to discover the most likely future in a demand planning scenario. I defined a good forecast as one that is unbiased and as accurate as possible. But I also cautioned that, depending on the stability or volatility of the data we have to work with, there may still be some inaccuracy in even a good forecast. The key is to have an understanding of how much.
This topic, managing uncertainty, is the subject of post by my colleague Tom Willemain, “The Average is not the Answer”. His post lays out the theory for responsibly confronting the limits of our predictive ability. It’s important to understand how this actually works.
As I briefly touched on at the end of my previous post, our approach begins with something called a “sliding simulation”. We estimate how accurately we are predicting the future by using our forecasting techniques on an older portion of history, excluding the most recent data. We can then compare what we would have predicted for the recent past with our actual real world information about what happened. This is a reliable method to estimate how closely we are predicting future demand.
Safety stock, a carefully measured buffer in inventory level we stock above our prediction of most likely demand, is derived from the estimate of forecast error coming out of the “sliding simulation”. This approach to dealing with the accuracy of our forecasts efficiently balances between ignoring the threat of the unpredictable and costly overcompensation.
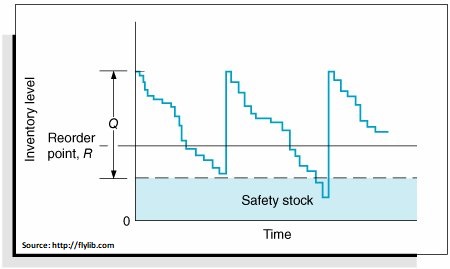In more technical detail: the forecasts errors that are estimated by this sliding simulation process indicate the level of uncertainty. We use these errors to estimate the standard deviation of the forecasts. Now, with regular demand, we can assume the forecasts (which are estimates of future behavior) are best represented by a bell-shaped probability distribution—what statisticians call the “normal distribution”. The center of that distribution is our point forecast. The width of that distribution is the standard deviation of the “sliding simulation” forecast from the known actual values—we obtain this directly from our forecast error estimates.
Once we know the specific bell shaped curve associated with the forecast, we can easily estimate the safety stock buffer that is needed. The only input from us is the “service level” that is desired, and the safety stock at that service level can be ascertained. (The service level is essentially a measure of how confident we need to be in our inventory stocking levels, with increasing confidence requiring corresponding expenditures on extra inventory.) Notice, we are assuming that the correct distribution to use is the normal distribution. This is correct for most demand series where you have regular demand per period. It fails when demand is sporadic or intermittent.
In the next piece in this series, I’ll discuss how Smart Forecasts deals with estimating safety stock in those cases of intermittent demand, when the assumption of normality is incorrect.
Nelson Hartunian, PhD, co-founded Smart Software, formerly served as President, and currently oversees it as Chairman of the Board. He has, at various times, headed software development, sales and customer service.
Related Posts
How to interpret and manipulate forecast results with different forecast methods
This blog explains how each forecasting model works using time plots of historical and forecast data. It outlines how to go about choosing which model to use. The examples below show the same history, in red, forecasted with each method, in dark green, compared to the Smart-chosen winning method, in light green.
What to do when a statistical forecast doesn’t make sense
Sometimes a statistical forecast just doesn’t make sense. Every forecaster has been there. They may double-check that the data was input correctly or review the model settings but are still left scratching their head over why the forecast looks very unlike the demand history. When the occasional forecast doesn’t make sense, it can erode confidence in the entire statistical forecasting process.
The Role of Trust in the Demand Forecasting Process Part 2: What do you Trust
Regardless of how much effort is poured into training forecasters and developing elaborate forecast support systems, decision-makers will either modify or discard the predictions if they do not trust them.”
Recent Posts
The top 3 reasons why your spreadsheet won’t work for optimizing reorder points on spare partsWe often encounter Excel-based reorder point planning methods. In this post, we’ve detailed an approach that a customer used prior to proceeding with Smart. We describe how their spreadsheet worked, the statistical approaches it relied on, the steps planners went through each planning cycle, and their stated motivations for using (and really liking) this internally developed spreadsheet. […]
How to interpret and manipulate forecast results with different forecast methodsThis blog explains how each forecasting model works using time plots of historical and forecast data. It outlines how to go about choosing which model to use. The examples below show the same history, in red, forecasted with each method, in dark green, compared to the Smart-chosen winning method, in light green. […]
Why Spare Parts Tradeoff Curves are Mission-Critical for Parts PlanningWhen managing service parts, you don’t know what will break and when because part failures are random and sudden. As a result, demand patterns are most often extremely intermittent and lack significant trend or seasonal structure. The number of part-by-location combinations is often in the hundreds of thousands, so it’s not feasible to manually review demand for individual parts. Nevertheless, it is much more straightforward to implement a planning and forecasting system to support spare parts planning than you might think. […]
What to do when a statistical forecast doesn’t make senseSometimes a statistical forecast just doesn’t make sense. Every forecaster has been there. They may double-check that the data was input correctly or review the model settings but are still left scratching their head over why the forecast looks very unlike the demand history. When the occasional forecast doesn’t make sense, it can erode confidence in the entire statistical forecasting process. […]
Spare Parts Planning Isn’t as Hard as You ThinkWhen managing service parts, you don’t know what will break and when because part failures are random and sudden. As a result, demand patterns are most often extremely intermittent and lack significant trend or seasonal structure. The number of part-by-location combinations is often in the hundreds of thousands, so it’s not feasible to manually review demand for individual parts. Nevertheless, it is much more straightforward to implement a planning and forecasting system to support spare parts planning than you might think. […]
Inventory Optimization for Manufacturers, Distributors, and MRO
- The top 3 reasons why your spreadsheet won’t work for optimizing reorder points on spare partsWe often encounter Excel-based reorder point planning methods. In this post, we’ve detailed an approach that a customer used prior to proceeding with Smart. We describe how their spreadsheet worked, the statistical approaches it relied on, the steps planners went through each planning cycle, and their stated motivations for using (and really liking) this internally developed spreadsheet. […]
- Why Spare Parts Tradeoff Curves are Mission-Critical for Parts PlanningWhen managing service parts, you don’t know what will break and when because part failures are random and sudden. As a result, demand patterns are most often extremely intermittent and lack significant trend or seasonal structure. The number of part-by-location combinations is often in the hundreds of thousands, so it’s not feasible to manually review demand for individual parts. Nevertheless, it is much more straightforward to implement a planning and forecasting system to support spare parts planning than you might think. […]
- Spare Parts Planning Isn’t as Hard as You ThinkWhen managing service parts, you don’t know what will break and when because part failures are random and sudden. As a result, demand patterns are most often extremely intermittent and lack significant trend or seasonal structure. The number of part-by-location combinations is often in the hundreds of thousands, so it’s not feasible to manually review demand for individual parts. Nevertheless, it is much more straightforward to implement a planning and forecasting system to support spare parts planning than you might think. […]
Service-Level-Driven Planning for Service Parts BusinessesService-Level-Driven Service Parts Planning is a four-step process that extends beyond simplified forecasting and rule-of-thumb safety stocks. It provides service parts planners with data-driven, risk-adjusted decision support. […]