In mijn vorige post in deze serie over essentiële concepten, “Wat is 'Een goede voorspelling'”besprak ik de basisinspanning om de meest waarschijnlijke toekomst te ontdekken in een scenario voor vraagplanning. Ik definieerde een goede voorspelling als een die onbevooroordeeld en zo nauwkeurig mogelijk is. Maar ik waarschuwde ook dat, afhankelijk van de stabiliteit of volatiliteit van de gegevens waarmee we moeten werken, er nog steeds enige onnauwkeurigheid kan zijn in zelfs een goede voorspelling. De sleutel is om inzicht te hebben in hoeveel.
Dit onderwerp, omgaan met onzekerheid, is het onderwerp van een bericht van mijn collega Tom Willemain, “Het gemiddelde is niet het antwoord”. Zijn post legt de theorie uiteen om op verantwoorde wijze de grenzen van ons voorspellende vermogen te confronteren. Het is belangrijk om te begrijpen hoe dit echt werkt.
Zoals ik aan het einde van mijn vorige bericht kort aanstipte, begint onze aanpak met iets dat een "glijdende simulatie" wordt genoemd. We schatten hoe nauwkeurig we de toekomst voorspellen door onze voorspellingstechnieken te gebruiken op een ouder deel van de geschiedenis, waarbij we de meest recente gegevens uitsluiten. We kunnen dan wat we zouden hebben voorspeld voor het recente verleden vergelijken met onze werkelijke informatie over wat er is gebeurd. Dit is een betrouwbare methode om in te schatten hoe nauwkeurig we de toekomstige vraag voorspellen.
Veiligheidsvoorraad, een zorgvuldig gemeten buffer in voorraadniveau die we in voorraad hebben boven onze voorspelling van de meest waarschijnlijke vraag, is afgeleid van de schatting van de voorspellingsfout die voortkomt uit de "glijdende simulatie". Deze aanpak om met de nauwkeurigheid van onze prognoses om te gaan, balanceert efficiënt tussen het negeren van de dreiging van onvoorspelbare en kostbare overcompensatie.
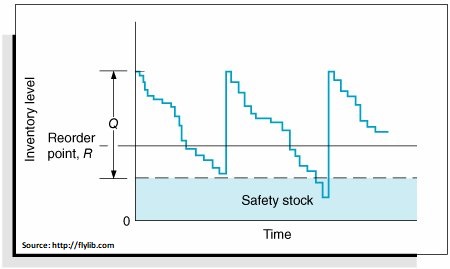 In meer technische details: de prognosefouten die worden geschat door dit glijdende simulatieproces geven het niveau van onzekerheid aan. We gebruiken deze fouten om de standaarddeviatie van de prognoses te schatten. Nu, met een regelmatige vraag, kunnen we aannemen dat de voorspellingen (die schattingen zijn van toekomstig gedrag) het beste worden weergegeven door een klokvormige kansverdeling - wat statistici de "normale verdeling" noemen. Het centrum van die verdeling is onze puntvoorspelling. De breedte van die verdeling is de standaarddeviatie van de "glijdende simulatie"-voorspelling van de bekende werkelijke waarden - we halen dit rechtstreeks uit onze schattingen van de voorspellingsfout.
In meer technische details: de prognosefouten die worden geschat door dit glijdende simulatieproces geven het niveau van onzekerheid aan. We gebruiken deze fouten om de standaarddeviatie van de prognoses te schatten. Nu, met een regelmatige vraag, kunnen we aannemen dat de voorspellingen (die schattingen zijn van toekomstig gedrag) het beste worden weergegeven door een klokvormige kansverdeling - wat statistici de "normale verdeling" noemen. Het centrum van die verdeling is onze puntvoorspelling. De breedte van die verdeling is de standaarddeviatie van de "glijdende simulatie"-voorspelling van de bekende werkelijke waarden - we halen dit rechtstreeks uit onze schattingen van de voorspellingsfout.
Zodra we de specifieke klokvormige curve kennen die bij de voorspelling hoort, kunnen we eenvoudig de benodigde veiligheidsvoorraadbuffer inschatten. De enige input van ons is het “serviceniveau” dat gewenst is en de veiligheidsvoorraad op dat serviceniveau kan worden bepaald. (Het serviceniveau is in wezen een maatstaf van hoe zeker we moeten zijn van onze voorraadniveaus, waarbij een groeiend vertrouwen corresponderende uitgaven voor extra voorraad vereist.) Let op, we gaan ervan uit dat de juiste verdeling die moet worden gebruikt de normale verdeling is. Dit is correct voor de meeste vraagreeksen waar u een regelmatige vraag per periode heeft. Het mislukt wanneer de vraag sporadisch of met tussenpozen is.
In het volgende stuk in deze serie zal ik bespreken hoe Smart Forecasts omgaat met het schatten van de veiligheidsvoorraad in die gevallen van intermitterende vraag, wanneer de veronderstelling van normaliteit onjuist is.
Nelson Hartunian, PhD, was medeoprichter van Smart Software, was voorheen President en houdt er momenteel toezicht op als voorzitter van de raad van bestuur. Hij heeft op verschillende momenten leiding gegeven aan softwareontwikkeling, verkoop en klantenservice.
gerelateerde berichten

Op prognoses gebaseerd voorraadbeheer voor een betere planning
Forecast-based inventory management, or MRP (Material Requirements Planning) logic, is a forward-planning method that helps businesses meet demand without overstocking or understocking. By anticipating demand and adjusting inventory levels, it maintains a balance between meeting customer needs and minimizing excess inventory costs. This approach optimizes operations, reduces waste, and enhances customer satisfaction.

Gebruikmaken van Epicor Kinetic Planning BOM's met Smart IP&O voor nauwkeurige prognoses
In deze blog onderzoeken we hoe het gebruik van Epicor Kinetic Planning BOM's met Smart IP&O uw benadering van forecasting in een zeer configureerbare productieomgeving kan transformeren. Ontdek hoe Smart, een geavanceerde AI-gestuurde oplossing voor vraagplanning en voorraadoptimalisatie, de complexiteit van het voorspellen van de vraag naar eindproducten kan vereenvoudigen, vooral als het om verwisselbare componenten gaat. Ontdek hoe het plannen van stuklijsten en geavanceerde prognosetechnieken bedrijven in staat stelt nauwkeuriger te anticiperen op de behoeften van klanten, waardoor de operationele efficiëntie wordt gewaarborgd en een voorsprong behouden in een concurrerende markt.
Dagelijkse vraagscenario's
In deze videoblog leggen we uit hoe tijdreeksvoorspellingen naar voren zijn gekomen als een cruciaal hulpmiddel, vooral op dagelijks niveau, waarmee Smart Software sinds de oprichting ruim veertig jaar geleden pionierde. De evolutie van bedrijfspraktijken van jaarlijkse naar meer verfijnde temporele stappen zoals maandelijkse en nu dagelijkse data-analyse illustreert een significante verschuiving in operationele strategieën.