You may remember the story of Goldilocks from your long-ago youth. Sometimes the porridge was too hot, sometimes it was too cold, but just once it was just right. Now that we are adults, we can translate that fairy tale into a professional principle for inventory planning: There can be too little or too much inventory, and there is some Goldilocks level that is “just right.” This blog is about finding that sweet spot.
To illustrate our supply chain fable, consider this example. Imagine that you sell service parts to keep your customers systems up and running. You offer a particular service part that costs you $100 to make but sells for a 20% markup. You can make $20 on each unit you sell, but you don’t get to keep the whole $20 because of the inventory operating costs you bear to be able to sell the part. There are holding costs to keep the part in good repair while in stock and ordering costs to replenish units you sell. Finally, sometimes you lose revenue from lost sales due to stockouts.
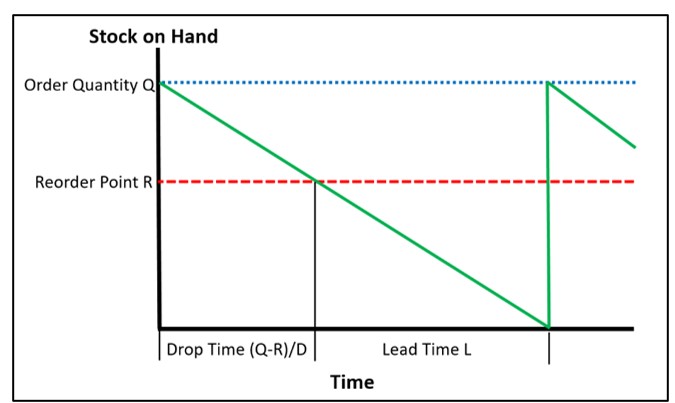
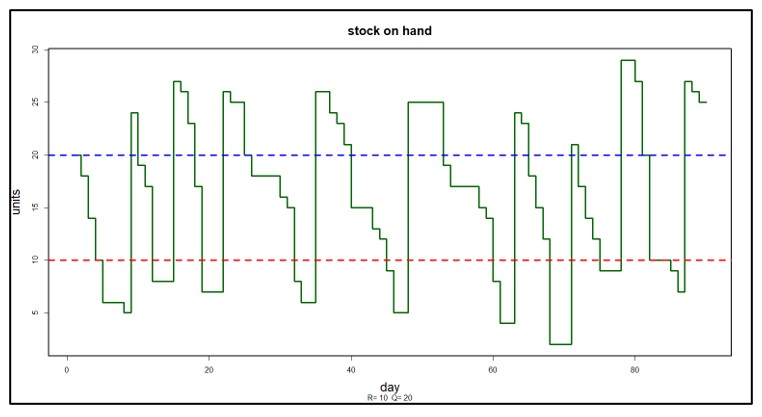
These operating costs can be directly related to the way you manage the part in inventory. For our example, assume you use a (Q,R) inventory policy, where Q is the replenishment order quantity and R is the reorder point. Assume further that the reason you are not making $30 per unit is that you have competitors, and customers will get the part from them if they can’t get it from you.
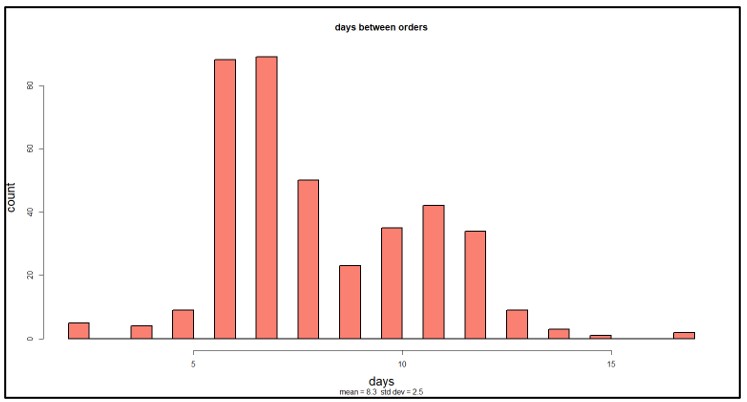
Both your revenue and your costs depend in complex ways on your choices for Q and R. These will determine how much you order, when and therefore how often you order, how often you stock out and therefore how many sales you lose, and how much cash you tie up in inventory. It is impossible to cost out these relationships by guesswork, but modern software can make the relationships visible and calculate the dollar figures you need to guide your choice of values for Q and R. It does this by running detailed, fact-based, probabilistic simulations that predict costs and performance by averaging over a large number of realistic demand scenarios.
With these results in hand, you can work out the margin associated with (Q,R) values using the simple formula
Margin = (Demand – Lost Sales) x Profit per unit sold – Ordering Costs – Holding Costs.
In this formula, Lost Sales, Ordering Costs and Holding Costs are dependent on reorder point R and order quantity Q.
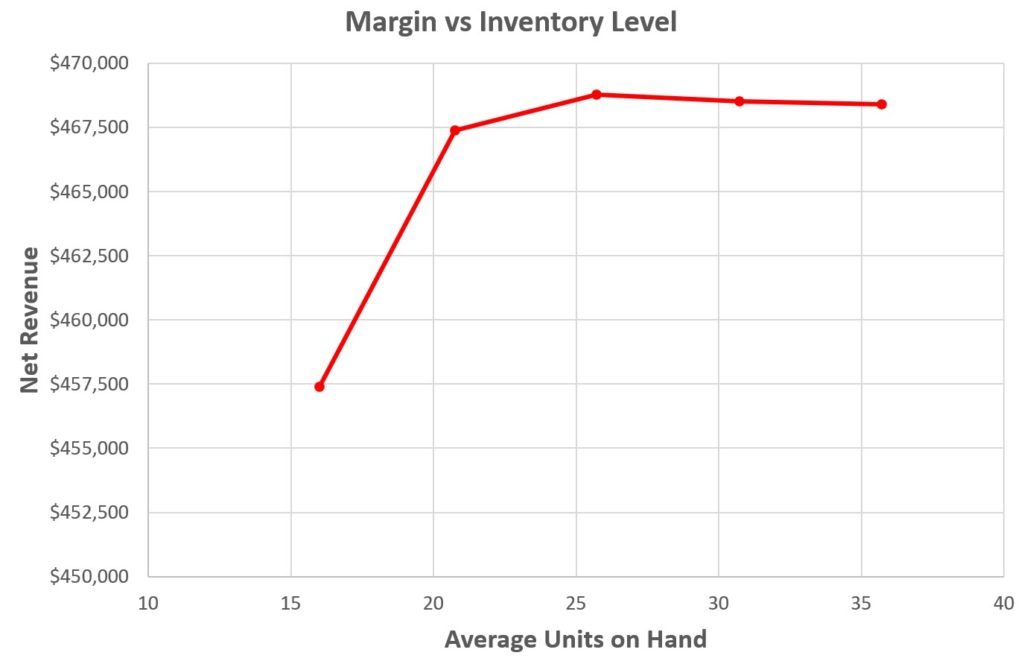
Figure 1 shows the result of simulations that fixed Q at 25 units and varied R from 10 to 30 in steps of 5. While the curve is rather flat on top, you would make the most money by keeping on-hand inventory around 25 units (which corresponds to setting R = 20). More inventory, despite a higher service level and fewer lost sales, would make a little less money (and ties up a lot more cash), and less inventory would make a lot less.
Without relying on the inventory simulation software, we would not be able to discover
- a) that it is possible to carry too little and too much inventory
- b) what the best level of inventory is
- c) how to get there by proper choices of reorder point R and order quantity Q.
Without an explicit understanding of the above, companies will make daily inventory decisions relying on gut feel and averaging based rule of thumb methods. The tradeoffs described here are not exposed and the resulting mix of inventory yields a far lower return forfeiting hundreds of thousands to millions per year in lost profits. So be like Goldilocks. With the right systems and software tools, you too can get it just right!

Forecast-Based Inventory Management for Better Planning
Forecast-based inventory management, or MRP (Material Requirements Planning) logic, is a forward-planning method that helps businesses meet demand without overstocking or understocking. By anticipating demand and adjusting inventory levels, it maintains a balance between meeting customer needs and minimizing excess inventory costs. This approach optimizes operations, reduces waste, and enhances customer satisfaction.

Make AI-Driven Inventory Optimization an Ally for Your Organization
In this blog, we will explore how organizations can achieve exceptional efficiency and accuracy with AI-driven inventory optimization. Traditional inventory management methods often fall short due to their reactive nature and reliance on manual processes. Maintaining optimal inventory levels is fundamental for meeting customer demand while minimizing costs. The introduction of AI-driven inventory optimization can significantly reduce the burden of manual processes, providing relief to supply chain managers from tedious tasks.

The Importance of Clear Service Level Definitions in Inventory Management
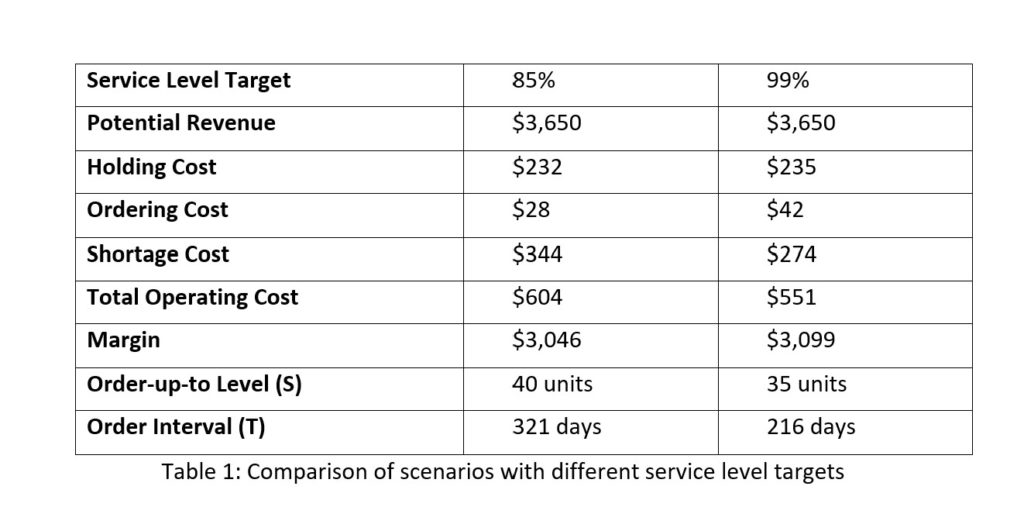
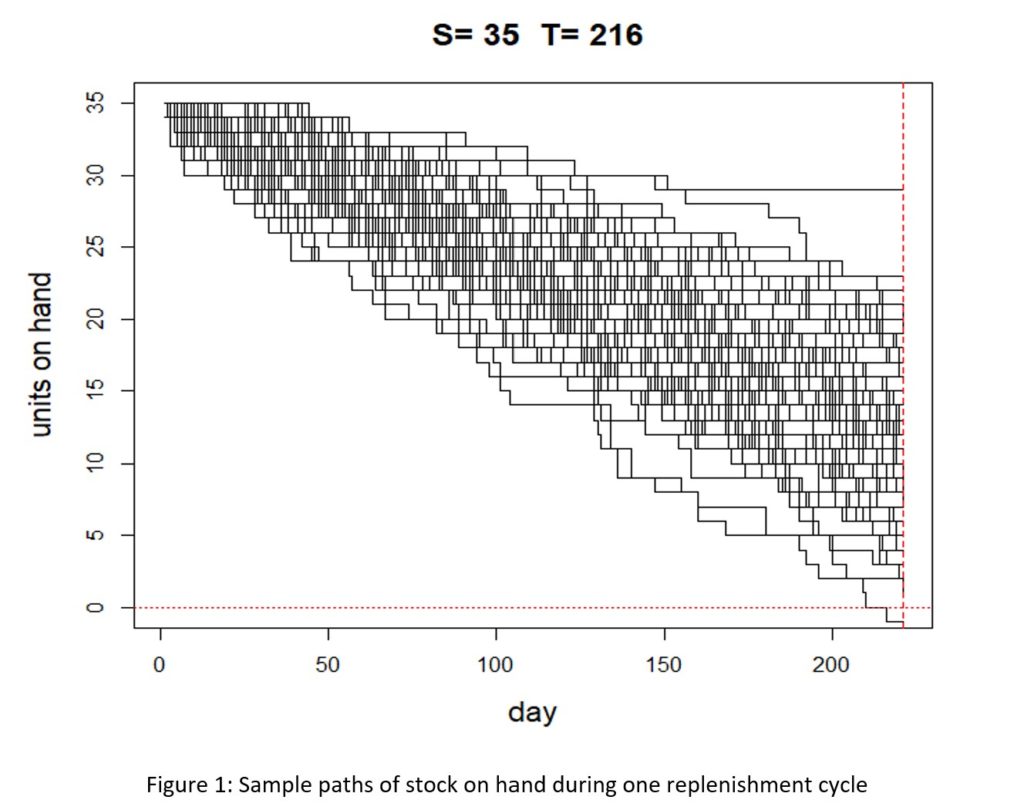
Inventory optimization software that supports what-if analysis will expose the tradeoff of stockouts vs. excess costs of varying service level targets. But first it is important to identify how “service levels” is interpreted, measured, and reported. This will avoid miscommunication and the false sense of security that can develop when less stringent definitions are used. Clearly defining how service level is calculated puts all stakeholders on the same page. This facilitates better decision-making.