Why Days of Supply Targets Don’t Work when Computing Safety Stocks

CFOs tell us they need to spend less on inventory without impacting sales.  One way to do that is to move away from using targeted day of supply to determine reorder points and safety stock buffers.   Here is how a days of supply model works:

1. Compute average demand per day and multiply the demand per day by supplier lead time in days to get lead time demand
2. Pick a days of supply buffer (i.e., 15, 30, 45 days, etc.). Use larger buffers being used for more important items and smaller buffers for less important items.
3. Add the desired days of supply buffer to demand over the lead time to get the reorder point. Order more when on hand inventory falls below the reorder point

Here is what is wrong with this approach:

1. The average doesn’t account for seasonality and trend – you’ll miss obvious patterns unless you spend lots of time manually adjusting for it.
2. The average doesn’t consider how predictable an item is – you’ll overstock predictable items and understock less predictable ones. This is because the same days of supply for different items yields a very different stock out risk.
3. The average doesn’t tell a planner how stock out risk is impacted by the level of inventory – you’ll have no idea whether you are understocked, overstocked, or have just enough. You are essentially planning with blinders on.

There are many other “rule of thumb” approaches that are equally problematic.  You can learn more about them in this post. 

A better way to plan the right amount of safety stock is to leverage probability models that identify exactly how much stock is needed given the risk of stock-out you are willing to accept.   Below is a screenshot of Smart Inventory Optimization that does exactly that.  First, it details the predicted service levels (probability of not stocking out) associated with the current days of supply logic.  The planner can now see the parts where predicted service level is too low or too costly.  They can then make immediate corrections by targeting the desired service levels and level of inventory investment. Without this information, a planner isn’t going to know whether the targeted days of safety stock is too much, too little, or just right resulting in overstocks and shortages that cost market share and revenue. 

Whether you understand it in detail yourself or rely on trustworthy software, math is a fact of life for anyone in inventory management and demand forecasting who is hoping to remain competitive in the modern world.

At a conference recently, the lead presenter in an inventory management workshop proudly proclaimed that he had no need for “high-fallutin’ math”, which was explained to mean anything beyond sixth-grade math.

Math is not everyone’s first love. But if you really care about doing your job well, you can’t approach the work with a grade school mentality. Supply chain tasks like demand forecasting and inventory management are inherently mathematical. The blog associated with edX, a premier site for online college course material, has a great post on this topic, at https://www.mooc.org/blog/how-is-math-used-in-supply-chain. Let me quote the first bit:

Math and the supply chain go hand and hand. As supply chains grow, increasing complexity will drive companies to look for ways to manage large-scale decision-making. They can’t go back to how supply chains were 100 years ago—or even two years ago before the pandemic. Instead, new technologies will help streamline and manage the many moving parts. The logistics skills, optimization technologies, and organizational skills used in supply chain all require mathematics.

Our customers don’t need to be experts in supply chain math, they just need to be able to wield the software that contains the math. Software combines users’ experience and subject matter expertise to produce results that make the difference between success and failure. To do its job, the software can’t stop at sixth-grade math; it needs probability, statistics, and optimization theory.

It’s up to us software vendors to package the math in such a way that what goes into the calculations is all that is relevant, even if complicated; and that what comes out is clear, decision-relevant, and defensible when you must justify your recommendations to higher management.

Sixth-grade math can’t warn you when the way you propose to manage a critical spare part will mean a 70% chance of falling short of your item availability target. It can’t tell you how best to adjust your reorder points when a supplier calls and says, “We have a delivery problem.” It can’t save your skin when there is a surprisingly large order and you have to quickly figure out the best way to set up some expedited special orders without busting the operating budget.

So, respect the folk wisdom and don’t bring a knife to a gunfight.

When deciding on the right stocking parameters for spare parts and service parts, it is important to distinguish between consumable and repairable service parts.  These differences are often overlooked by service parts planning software and can result in incorrect estimates of what to stock.  Different approaches are required when planning for consumables vs. repairable spare parts.

First, let’s define these two types of spare parts.

• Consumable parts are spares contained within the equipment which are replaced rather than repaired when they fail. Examples of consumable parts include batteries, oil filters, screws, and brake pads.  Consumable spare parts tend to be lower-cost parts for which replacement is cheaper than repair or repair may not be possible.
• Repairable parts are parts that are capable of being repaired and returned to service after failing due to causes like wear and tear, damage, or corrosion. Repairable service parts tend to be more expensive than consumable parts, so repair is usually preferable to replacement. Examples of repairable parts include traction motors in rail cars, jet engines, and copy machines.

Traditional spare parts planning software fail to do the job

Traditional parts planning software is not well-adapted to deal with the randomness in both the demand side and the supply side of MRO operations.

Demand-Side Randomness
Planning for consumable spare parts requires calculation of inventory control parameters (such as reorder points and order quantities, min and max levels, and safety stocks). Planning to manage repairable service parts requires calculation of the right number of spares. In both cases, the analysis must be based on probability models of the random usage of consumables or the random breakdown of repairable parts.  For over 90% of these parts, this random demand is “intermittent” (sometimes called “lumpy” or “anything but normally distributed”). Traditional spare parts forecasting methods were not developed to deal with intermittent demand. Relying on traditional methods leads to costly planning mistakes. For consumables, this means avoidable stockouts, excess carrying costs, and increased inventory obsolescence. For repairable parts, this means excessive equipment downtime and the attendant costs from unreliable performance and disruption of operations.

Supply-Side Randomness
Planning for consumable spare parts must take account of randomness in replenishment lead times from suppliers. Planning for repairable parts must account for randomness in repair and return processes, whether provided internally or contracted out. Planners managing these items often ignore exploitable company data. Instead, they may cross their fingers and hope everything works out, or they may call on gut instinct to “call audibles” and then hope everything works out.  Hoping and guessing cannot beat proper probability modeling. It wastes millions annually in unneeded capital investments and avoidable equipment downtime.

Whether you are using ‘Min/Max’ or ‘reorder point’ and ‘order quantity’ to determine when and how much to restock, your approach might deliver or deny huge efficiencies. Key mistakes to avoid:

1. Not recalibrating regularly
2. Only reviewing Min/Max when there is a problem
3. Using Forecasting methods not up to the task
4. Assuming data is too slow moving or unpredictable for it to matter

“We have over 150,000 SKU x Location combinations. Our demand is intermittent. Since it’s slow moving, we don’t need to recalculate our reorder points often. We do so maybe once annually but review the reorder points whenever there is a problem.” – Materials Manager.

This reactive approach will lead to millions in excess stock, stock outs, and lots of wasted time reviewing data when “something goes wrong.” Yet, I’ve heard this same refrain from so many inventory professionals over the years. Clearly, we need to do more to share why this thinking is so problematic.

It is true that for many parts, a recalculation of the reorder points with up-to-date historical data and lead times might not change much, especially if patterns such as trend or seasonality aren’t present. However, many parts will benefit from a recalculation, especially if lead times or recent demand has changed. Plus, the likelihood of significant change that necessitates a recalculation increases the longer you wait. Finally, those months with zero demands also influence the probabilities and shouldn’t be ignored outright. The key point though is that it is impossible to know what will change or won’t change in your forecast, so it’s better to recalibrate regularly.

This standout case from real world data illustrates a scenario where regular and automated recalibration shines—the benefits from quick responses to changing demand patterns like these add up quickly. In the above example, the X axis represents days, and the Y axis represents demand. If you were to wait several months between recalibrating your reorder points, you’d undoubtedly order far too soon. By recalibrating your reorder point far more often, you’ll catch the change in demand enabling much more accurate orders.

Rather than wait until you have a problem, recalibrate all parts every planning cycle at least once monthly. Doing so takes advantage of the latest data and proactively adjusts the stocking policy, thus avoiding problems that would cause manual reviews and inventory shortages or excess.

The nature of your (potentially varied) data also needs to be matched with the right forecasting tools. If records for some parts show trend or seasonal patterns, using targeting forecasting methods to accommodate these patterns can make a big difference. Similarly, if the data show frequent zero values (intermittent demand), forecasting methods not built around this special case can easily deliver unreliable results.

Automate, recalibrate and review exceptions. Purpose built software will do this automatically. Think of it another way: is it better to dump a bunch of money into your 401K once per year or “dollar cost average” by depositing smaller, equally sized amounts throughout the year. Recalibrating policies regularly will yield maximized returns over time, just as dollar cost averaging will do for your investment portfolio.

How often do you recalibrate your stocking policies? Why?

​If you hear the phrase “regime change” on the news, you immediately think of some fraught geopolitical event. Statisticians use the phrase differently, in a way that has high relevance for demand planning and inventory optimization. This blog is about “regime change” in the statistical sense, meaning a major change in the character of the demand for an inventory item.

An item’s demand history is the fuel that powers demand planners’ forecasting machines. In general, the more fuel the better, giving us a better fix on the average level, the volatility, the size and frequency of any spikes, the shape of any seasonality pattern, and the size and direction of any trend.

But there is one big exception to the rule that “more data is better data.” If there is a major shift in your world and new demand doesn’t look like old demand, then old data become dangerous.

Modern software can make accurate forecasts of item demand and suggest wise choices for inventory parameters like reorder points and order quantities. But the validity of these calculations depends on the relevance of the data used in their calculation. Old data from an old regime no longer reflect current reality, so including them in calculations creates forecast error for demand planners and either excess stock or unacceptable stockout rates for inventory planners.

That said, if you were to endure a recent regime change and throw out the obsolete data, you would have a lot less data to work with. This has its own costs, because all the estimates computed from the data would have greater statistical uncertainty even though they would be less biased. In this case, your calculations would have to rely more heavily on a blend of statistical analysis and your own expert judgement.

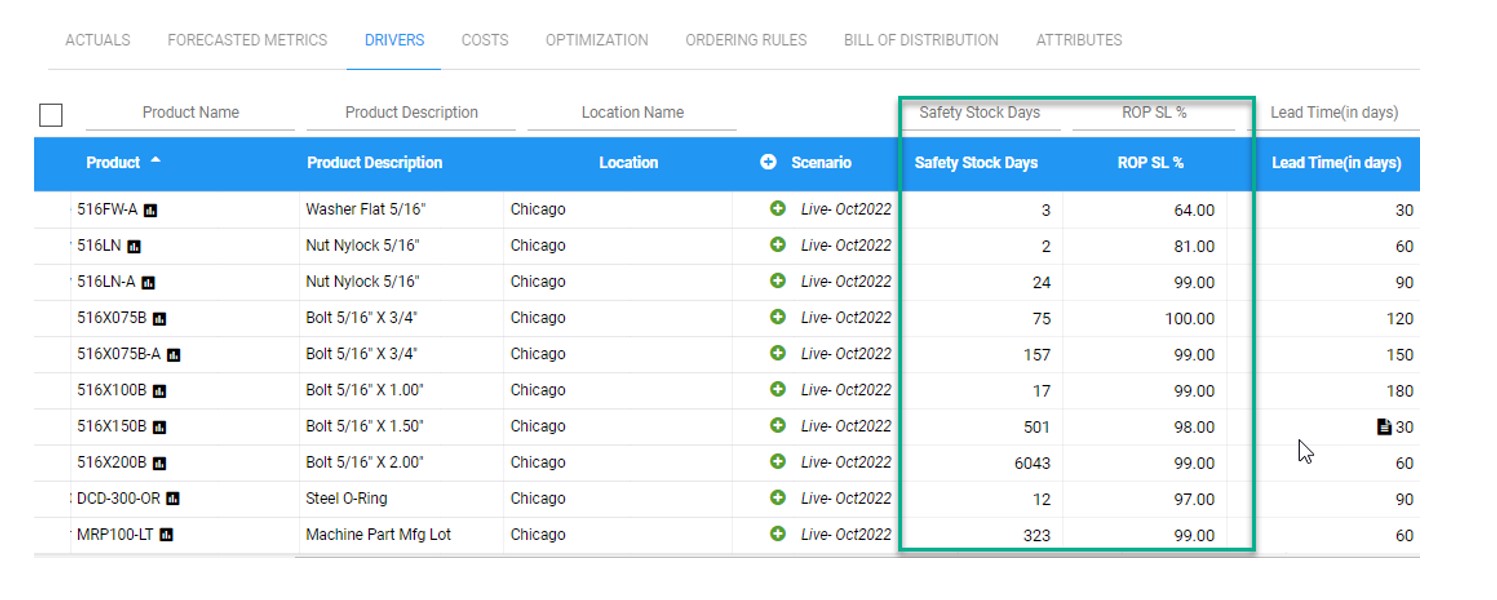
At this point, you may ask “How can I know if and when there has been a regime change?” If you’ve been on the job for a while and are comfortable looking at timeplots of item demand, you will generally recognize regime change when you see it, at least if it’s not too subtle. Figure 1 shows some real-world examples that are obvious.

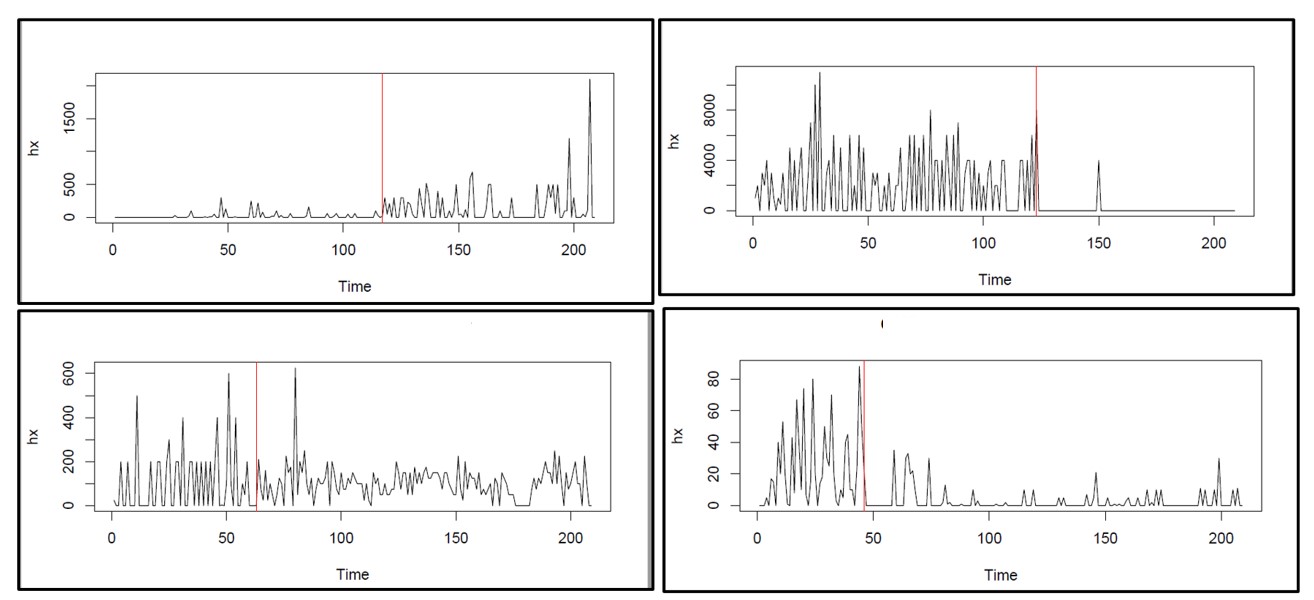
Figure 1: Four examples of regime change in real-world item demand

Unfortunately, less obvious changes can still have significant effects. Moreover, most of our customers are too busy to manually review all the items they manage even once per quarter. When you get beyond, say, 100 items, the task of eyeballing all those time series becomes onerous. Fortunately, software can do a good job of continuously monitoring demand for tens of thousands of items and alerting you to any items that may need your attention. Then too, you can arrange for the software to not only detect regime change but also automatically exclude from its calculations all data collected before the most recent regime change, if any. In other words, you can get both automatic warning of regime change and automatic protection from regime change.

For more on the basics of regime change, see our previous blog on the topic: https://smartcorp.com/blog/demandplanningregimechange/  

An Example with Numbers in It

If you would like to learn more, read on to see a numerical example of how much regime change can alter the calculation of a reorder point for a critical spare part. Here is a scenario to illustrate the point.

Scenario

• Goal: calculate the reorder point needed to control the risk of stockout while waiting for replenishment. Assume the target stockout risk is 5%.
• Assume the item has intermittent daily demand, with many days of zero demand.
• Assume daily demand has a Poisson distribution with an average of 1.0 units per day.
• Assume the replenishment lead time is always 30 days.
• The lead time demand will be random, so it will have a probability distribution and the reorder point will be the 95^th percentile of the distribution.
• Assume the effect of regime change is to either raise or lower the mean daily demand.
• Assume there is one year of daily data available for estimating the mean daily unit demand.

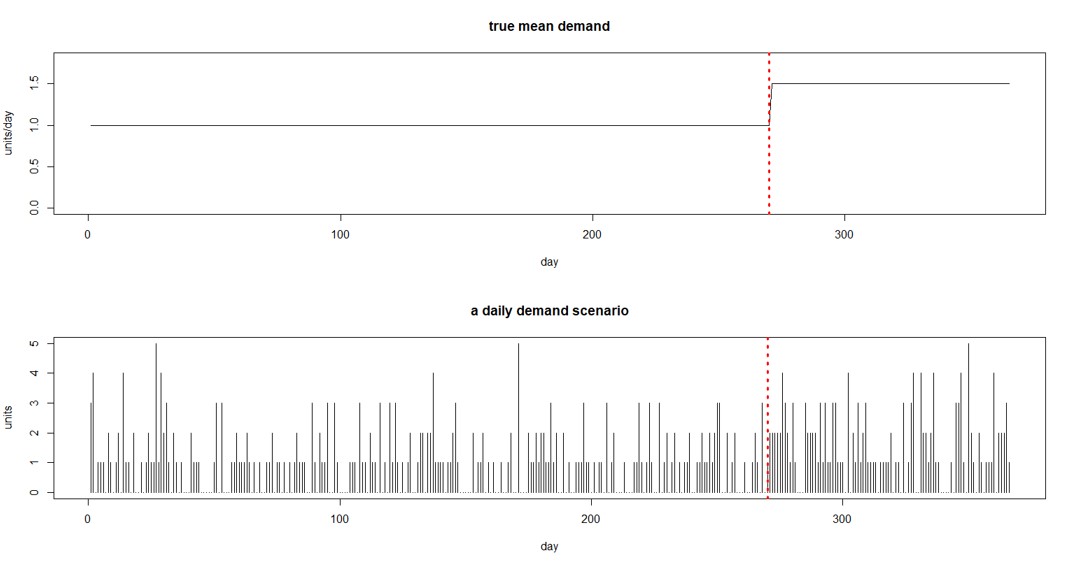
Figure 2 Example of change in mean demand and sample of random daily demand

Figure 2 shows one form of this scenario. The top panel shows that the average daily demand increases from 1.0 to 1.5 after 270 days. The bottom panel shows one way that a year’s worth of daily demand might appear. (At this point, you may be feeling that calculating all this stuff is complicated, even for what turns out to be a simplified scenario. That is why we have software!)

Analysis

Successful calculation of the proper reorder point will depend on when regime change happens and how big a change occurs. We simulated regime changes of various sizes at various times within a 365 day period. Around a base demand of 1.0 units per day, we studied shifts in demand (“shift”) of ±25% and ±50% as well as a no change reference case. We located the time of the change (“t.break”) at 90, 180, and 270 days. In each case, we computed two estimates of the reorder point: The “ideal” value given perfect knowledge of the average demand in the new regime (“ROP.true”), and the estimated value of mean demand computed by ignoring the regime change and using all the demand data for the past year (“ROP.all”).

Table 1 shows the estimates of the reorder point computed over 100 simulations. The center block is the reference case, in which there is no change in the daily demand, which remains fixed at 1 unit per day. The colored block at the bottom is the most extreme increasing scenario, with demand increasing to 1.5 units/day either one-third, one-half, or two-thirds of the way through the year.

We can draw several conclusions from these simulations.

ROP.true: The correct choice for reorder point increases or decreases according to the change in mean demand after the regime change. The relationship is not a simple linear one: the table spans a 600% range of demand levels (0.25 to 1.50) but a 467% range of reorder points (from 12 to 56).

ROP.all: Ignoring the regime change can lead to gross overestimates of the reorder point when demand drops and gross underestimates when demand increases.  As we would expect, the later the regime change, the worse the error. For example, if demand increases from 1.0 to 1.5 units per day two-thirds of the way through the year without being noticed, the calculated reorder point of 43 units would fall 13 units short of where it should be.

A word of caution: Table 1 shows that basing the calculations of reorder points using only data from after a regime change will usually get the right answer. What it doesn’t show is that the estimates can be unstable if there is very little demand history after the change. Therefore, in practice, you should wait to react to the regime change until a decent number of observations have accumulated in the new regime. This might mean using all the demand history, both pre- and post-change, until, say, 60 or 90 days of history have accumulated before ignoring pre-change data.

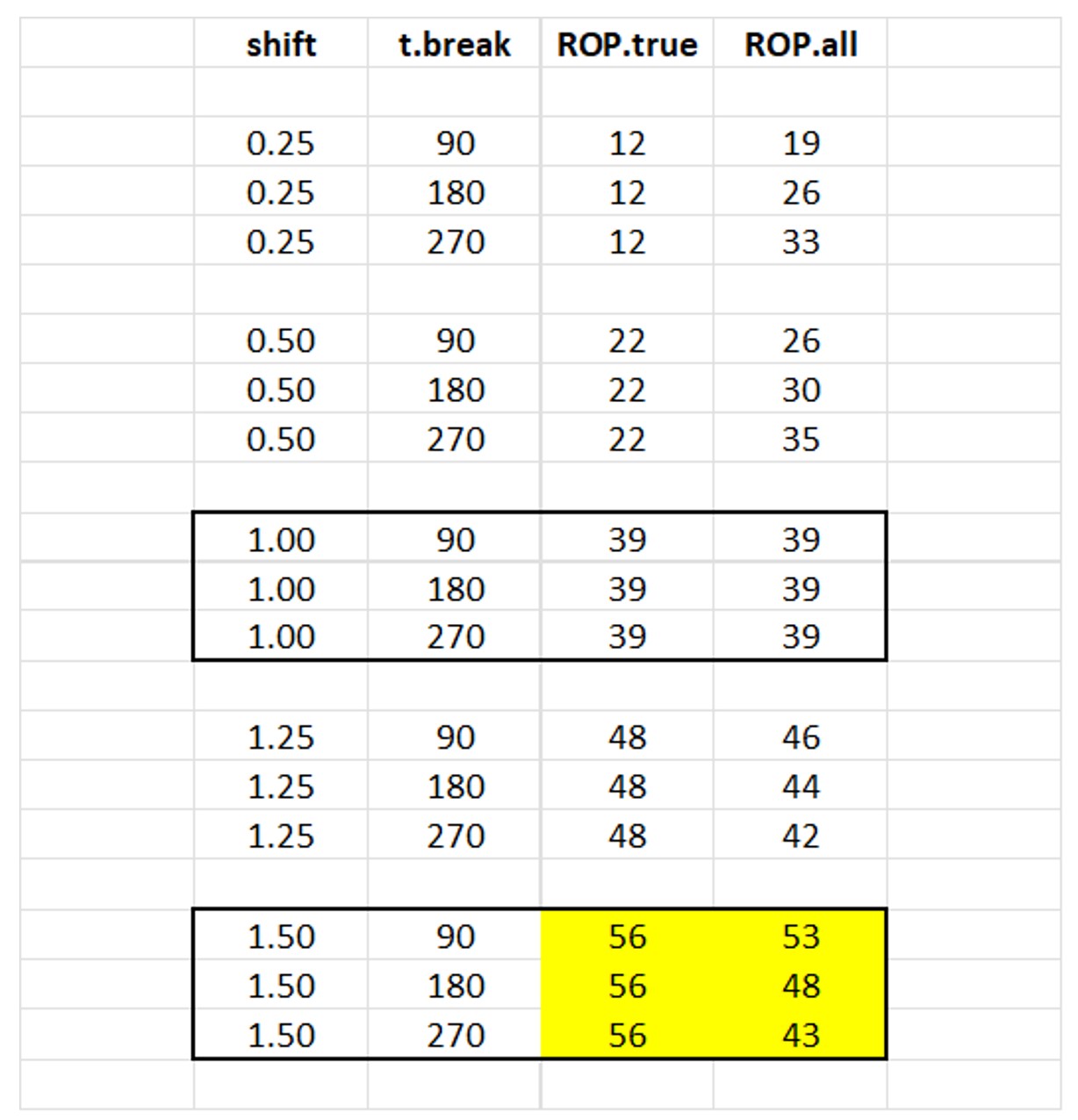
Table 1 Correct and Estimated Reorder Points for different regime change scenarios