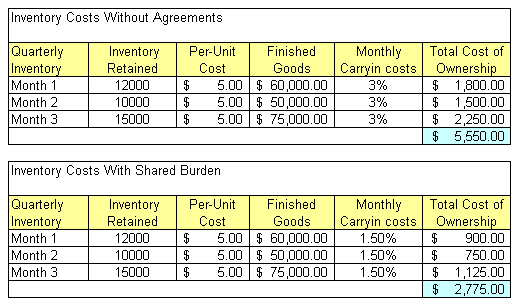
An Example of Simulation-Based Multiechelon Inventory Optimization

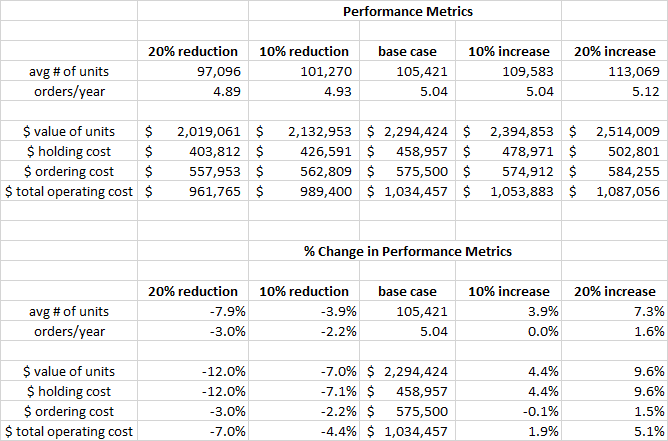
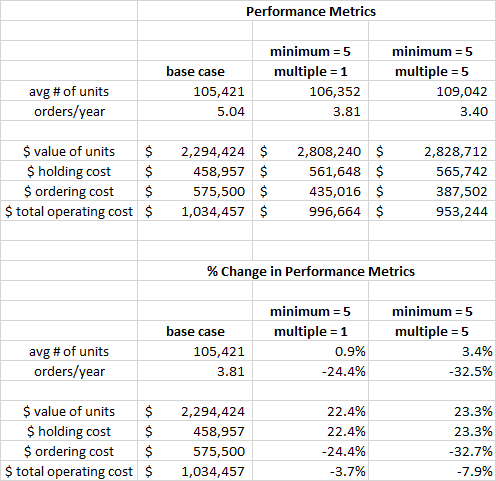
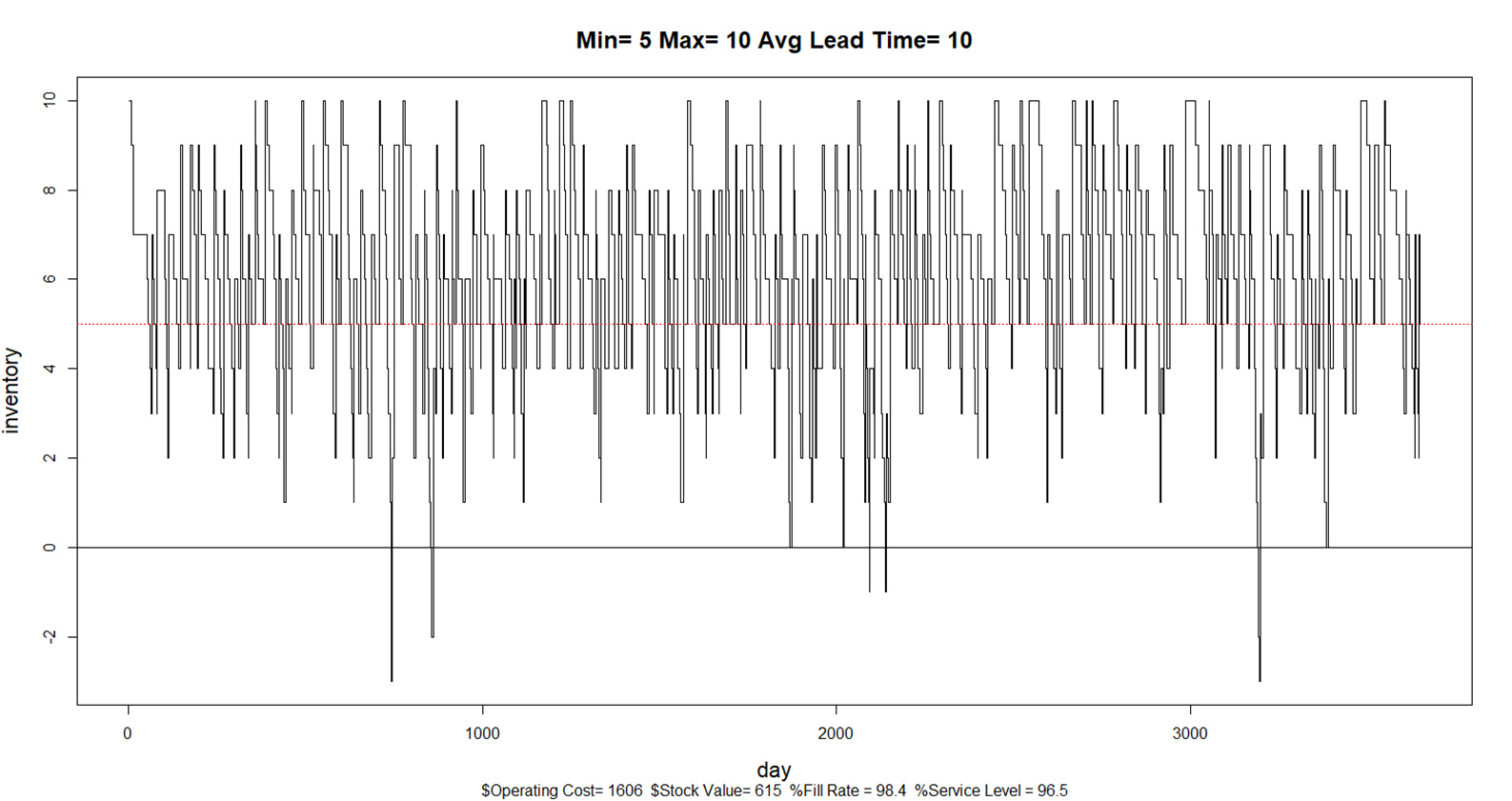
Managing the inventory in a single facility is difficult enough, but the problem becomes much more complex when there are multiple facilities arrayed in multiple echelons. The complexity arises from the interactions among the echelons, with demands at the lower levels bubbling up and any shortages at the higher levels cascading down.

If each of the facilities were to be managed in isolation, standard methods could be used, without regard to interactions, to set inventory control parameters such as reorder points and order quantities. However, ignoring the interactions between levels can lead to catastrophic failures. Experience and trial and error allow the design of stable systems, but that stability can be shattered by changes in demand patterns or lead times or by the addition of new facilities. Coping with such changes is greatly aided by advanced supply chain analytics, which provide a safe “sandbox” within which to test out proposed system changes before deploying them. This blog illustrates that point.

The Scenario

To have some hope of discussing this problem usefully, this blog will simplify the problem by considering the two-level hierarchy pictured in Figure 1. Imagine the facilities at the lower level to be warehouses (WHs) from which customer demands are meant to be satisfied, and that the inventory items at each WH are service parts sold to a wide range of external customers.

Figure 1: General structure of one type of two-level inventory system

Imagine the higher level to consist of a single distribution center (DC) which does not service customers directly but does replenish the WHs. For simplicity, assume the DC itself is replenished from a Source that always has (or makes) sufficient stock to immediately ship parts to the DC, though with some delay. (Alternatively, we could consider the system to have retail stores supplied by one warehouse).

Each level can be described in terms of demand levels (treated as random), lead times (random), inventory control parameters (here, Min and Max values) and shortage policy (here, backorders allowed).

The Method of Analysis

The academic literature has made progress on this problem, though usually at the cost of simplifications necessary to facilitate a purely mathematical solution. Our approach here is more accessible and flexible: Monte Carlo simulation. That is, we build a computer program that incorporates the logic of the system operation. The program “creates” random demand at the WH level, processes the demand according to the logic of a chosen inventory policy, and creates demand for the DC by pooling the random requests for replenishment made by the WHs. This approach lets us observe many simulated days of system operation while watching for significant events like stockouts at either level.

An Example

To illustrate an analysis, we simulated a system consisting of four WHs and one DC. Average demand varied across the WHs. Replenishment from the DC to any WH took from 4 to 7 days, averaging 5.15 days. Replenishment of the DC from the Source took either 7, 14, 21 or 28 days, but 90% of the time it was either 21 or 28 days, making the average 21 days. Each facility had Min and Max values set by analyst judgement after some rough calculations.

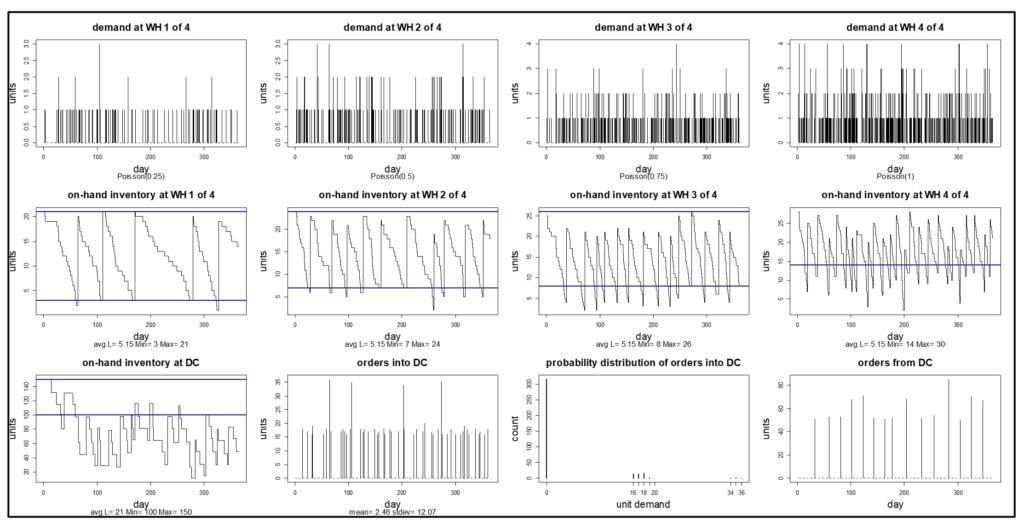
Figure 2 shows the results of one year of simulated daily operation of this system. The first row in the figure shows the daily demand for the item at each WH, which was assumed to be “purely random”, meaning it had a Poisson distribution. The second row shows the on-hand inventory at the end of each day, with Min and Max values indicated by blue lines. The third row describes operations at the DC. Contrary to the assumption of much theory, the demand into the DC was not close to being Poisson, nor was the demand out of the DC to the Source. In this scenario, Min and Max values were sufficient to keep item availability was high at each WH and at the DC, with no stockouts observed at any of the five facilities.

Click here to enlarge the image

Figure 2 – Simulated year of operation of a system with four WHs and one DC.

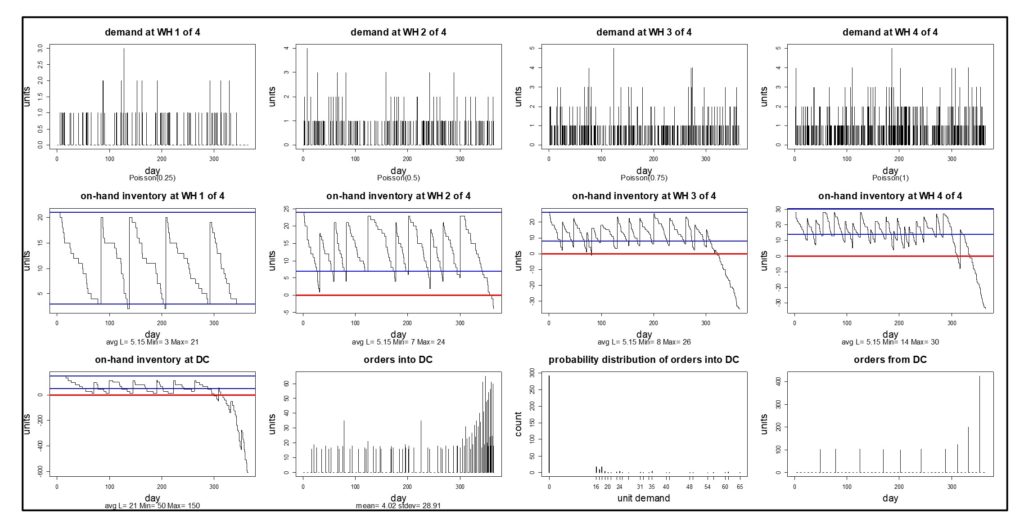
Now let’s vary the scenario. When stockouts are extremely rare, as in Figure 2, there is often excess inventory in the system. Suppose somebody suggests that the inventory level at the DC looks a bit fat and thinks it would be good idea to save money there. Their suggestion for reducing the stock at the DC is to reduce the value of the Min at the DC from 100 to 50. What happens? You could guess, or you could simulate.

Figure 3 shows the simulation – the result is not pretty. The system runs fine for much of the year, then the DC runs out of stock and cannot catch up despite sending successively larger replenishment orders to the Source. Three of the four WHs descend into death spirals by the end of the year (and WH1 follows thereafter). The simulation has highlighted a sensitivity that cannot be ignored and has flagged a bad decision.

Click here to enlarge image

Figure 3 – Simulated effects of reducing the Min at the DC.

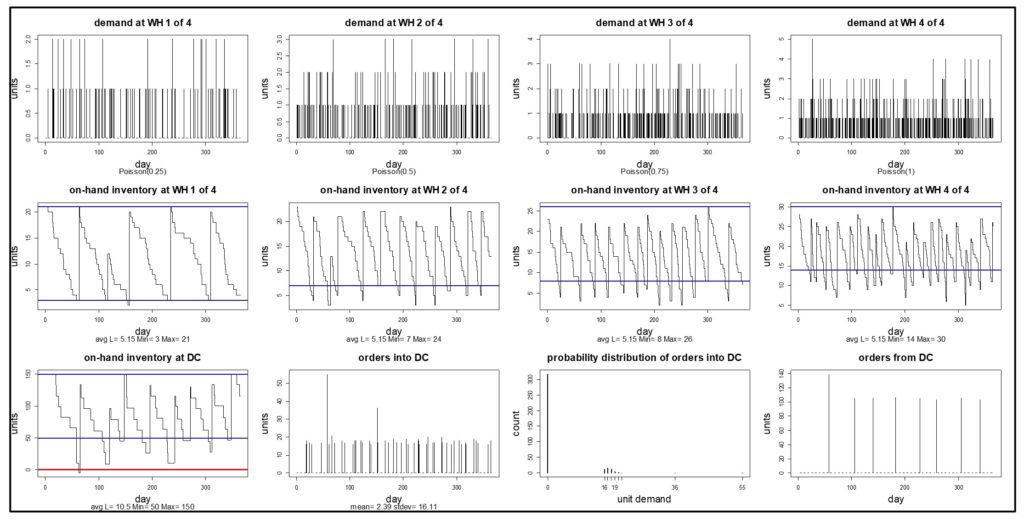
Now the inventory managers can go back to the drawing board and test out other possible ways to reduce the investment in inventory at the DC level. One move that always helps, if you and your supplier can jointly make it happen, is to create a more agile system by reducing replenishment lead time. Working with the Source to insure that the DC always gets its replenishments in either 7 or 14 days stabilizes the system, as shown in Figure 4.

Click here to enlarge image

Figure 4 – Simulated effects of reducing the lead time for replenishing the DC.

Unfortunately, the intent of reducing the inventory at the DC has not been achieved. The original daily inventory count was about 80 units and remains about 80 units after reducing the DC’s Min and drastically improving the Source-to-DC lead time. But with the simulation model, the planning team can try out other ideas until they arrive at a satisfactory redesign. Or, given that Figure 4 shows the DC inventory starting to flirt with zero, they might think it prudent to accept the need for an average of about 80 units at the DC and look for ways to trim inventory investment at the WHs instead.

The Takeaways

Multiechelon inventory optimization (MEIO) is complex. Many factors interact to produce system behaviors that can be surprising in even simple two-level systems.
Monte Carlo simulation is a useful tool for planners who need to design new systems or tweak existing systems.

Leave a Comment

The Next Frontier in Supply Chain Analytics

We believe the leading edge of supply chain analytics to be the development of digital twins of inventory systems. These twins take the form of discrete event models that use Monte Carlo simulation to generate and optimize over the full range of operational risks. We also assert that we and our colleagues at Smart Software have played an outsized role in forging that leading edge.

Overcoming Uncertainty with Service and Inventory Optimization Technology

In this blog, we will discuss today’s fast-paced and unpredictable market and the constant challenges businesses face in managing their inventory and service levels efficiently. The main subject of this discussion, rooted in the concept of “Probabilistic Inventory Optimization,” focuses on how modern technology can be leveraged to achieve optimal service and inventory targets amidst uncertainty. This approach not only addresses traditional inventory management issues but also offers a strategic edge in navigating the complexities of demand fluctuations and supply chain disruptions.

Centering Act: Spare Parts Timing, Pricing, and Reliability

In this article, we’ll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We’ll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we’ll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we’ll explore ways to enhance your service-level-driven inventory plan consistently.

Fact and Fantasy in Multiechelon Inventory Optimization

For most small-to-medium manufacturers and distributors, single-level or single-echelon inventory optimization is at the cutting edge of logistics practice. Multi-echelon inventory optimization (“MEIO”) involves playing the game at an even higher level and is therefore much less common. This blog is the first of two. It aims to explain what MEIO is, why standard MEIO theories break down, and how probabilistic modeling through scenario simulation can restore reality to the MEIO process. The second blog will show a particular example.

Definition of Inventory Optimization

An inventory system is built on a set of design choices.

The first choice is the policy for responding to stockouts: Do you just lose the sale to a competitor, or can you convince the customer to accept a backorder? The former is more common with distributors than manufacturers, but this may not be much of a choice since customers may dictate the answer.

The second choice is the inventory policy. These divide into “continuous review” and “periodic review” policies, with several options within each type. You can link to a video tutorial describing several common inventory policies here. Perhaps the most efficient is known to practitioners as “Min/Max” and to academics as (s, S) or “little S, Big S.” We use this policy in the scenario simulations below. It works as follows: When on-hand inventory drops to or below the Min (s), an order is placed for replenishment. The size of the order is the gap between the on-hand inventory and the Max (S), so if Min is 10, Max is 25 and on-hand is 8, it’s time for an order of 25-8 = 17 units.

The third choice is to decide on the best values of the inventory policy “parameters”, e.g., the values to use for Min and Max. Before assigning numbers to Min and Max, you need clarity on what “best” means for you. Commonly, best means choices that minimize inventory operating costs subject to a floor on item availability, expressed either as Service Level or Fill Rate. In mathematical terms, this is a “two-dimensional constrained integer optimization problem”. “Two-dimensional” because you have to pick two numbers: Min and Max. “Integer” because Min and Max have to be whole numbers. “Constrained” because you must pick Min and Max values that give a high-enough level of item availability such as service levels and fill rates. “Optimization” because you want to get there with the lowest operating cost (operating cost combines holding, ordering and shortage costs).

Multiechelon Inventory Systems

The optimization problem becomes more difficult in multi-echelon systems. In a single-echelon system, each inventory item can be analyzed in isolation: one pair of Min/Max values per SKU. Because there are more parts to a multiechelon system, there is a bigger computational problem.

Figure 1 shows a simple two-level system for managing a single SKU. At the lower level, demands arrive at multiple warehouses. When those are in danger of stocking out, they are resupplied from a distribution center (DC). When the DC itself is in danger of stocking out, it is supplied by some outside source, such as the manufacturer of the item.

The design problem here is multidimensional: We need Min and Max values for 4 warehouses and for the DC, so the optimization occurs in 4×2+1×2=10 dimensions. The analysis must take account of a multitude of contextual factors:

The average level and volatility of demand coming into each warehouse.
The average and variability of replenishment lead times from the DC.
The average and variability of replenishment lead times from the source.
The required minimum service level at the warehouses.
The required minimum service level at the DC.
The holding, ordering and shortage costs at each warehouse.
The holding, ordering and shortage costs at the DC.

As you might expect, seat-of-the-pants guesses won’t do well in this situation. Neither will trying to simplify the problem by analyzing each echelon separately. For instance, stockouts at the DC increase the risk of stockouts at the warehouse level and vice versa.

This problem is obviously too complicated to try to solve without help from some sort of computer model.

Why Standard Inventory Theory is Bad Math

With a little looking, you can find models, journal articles and book about MEIO. These are valuable sources of information and insight, even numbers. But most of them rely on the expedient of over-simplifying the problem to make it possible to write and solve equations. This is the “Fantasy” referred to in the title.

Doing so is a classic modeling maneuver and is not necessarily a bad idea. When I was a graduate student at MIT, I was taught the value of having two models: a small, rough model to serve as a kind of sighting scope and a larger, more accurate model to produce reliable numbers. The smaller model is equation-based and theory-based; the bigger model is procedure-based and data-based, i.e., a detailed system simulation. Models based on simple theories and equations can produce bad numerical estimates and even miss whole phenomena. In contrast, models based on procedures (e.g., “order up to the Max when you breach the Min”) and facts (e.g., the last 3 years of daily item demand) will require a lot more computing but give more realistic answers. Luckily, thanks to the cloud, we have a lot of computing power at our fingertips.

Perhaps the greatest modeling “sin” in the MEIO literature is the assumption that demands at all echelons can be modeled as purely random Poisson processes. Even if it were true at the warehouse level, it would be far from true at the DC level. The Poisson process is the “white rat of demand modeling” because it is simple and permits more paper-and-pencil equation manipulation. Since not all demands are Poisson shaped, this results in unrealistic recommendations.

Scenario-based Simulation Optimization

To get realism, we must get down into the details of how the inventory systems operate at each echelon. With few limits except those imposed by hardware such as size of memory, computer programs can keep up any level of complexity. For instance, there is no need to assume that each of the warehouses faces identical demand streams or has the same costs as all the others.

A computer simulation works as follows.

The real-world demand history and lead time history are gathered for each SKU at each location.
Values of inventory parameters (e.g., Min and Max) are selected for trial.
The demand and replenishment histories are used to create scenarios depicting inputs to the computer program that encodes the rules of operation of the system.
The inputs are used to drive the operation of a computer model of the system with the chosen parameter values over a long period, say one year.
Key performance indicators (KPI’s) are calculated for the simulated year.
Steps 2-5 are repeated many times and the results averaged to link parameter choices to system performance.

Inventory optimization adds another “outer loop” to the calculations by systematically searching over the possible values of Min and Max. Among those parameter pairs that satisfy the item availability constraint, further search identifies the Min and Max values that result in the lowest operating cost.

Figure 1: General structure of one type of two-level inventory system

Stay Tuned for our next Blog

COMING SOON. To see an example of a simulation of the system in Figure 1, read the second blog on this topic

Leave a Comment

The Next Frontier in Supply Chain Analytics

Overcoming Uncertainty with Service and Inventory Optimization Technology

Centering Act: Spare Parts Timing, Pricing, and Reliability

Assessing How Suppliers Influence Your Inventory Costs

The Smart Forecaster

Pursuing best practices in demand planning,

forecasting and inventory optimization

Software for inventory optimization is most often used to crank out the analytical results you need to run your day-to-day business, such as Reorder Points (also known as Mins) and Order Quantities. This specialized software helps you find the sweet spot that balances inventory costs against item availability during routine operations.

Inventory optimization software can also be used to perform “what-if” analyses on scenarios that describe changes from your current operating environment. What-if analysis (also called “sensitivity analysis”) lets you elevate your thinking from the tactical to the strategic. It helps you imagine how you should change your operations to adapt to potential changes in your operating environment. These changes might be negative pressures imposed on you from the outside, or they might result from your own positive actions. In this blog, we provide an example of how to conduct “what-analysis” on lead times and order quantities. Outputs from the analysis can be used by the business to assess the impact of these changes on inventory costs and service level performance.

How Suppliers Limit Your Freedom of Maneuver

Discussing with our customers the data inputs required by inventory optimization software, we noted that suppliers are a prominent influence on their operations. We leave aside for now such important topics as sharing demand forecasts with suppliers and working out responses to supply chain disruptions, such as Hurricane Matthew last year in the southeastern US. Instead, we focus on two more common ways that suppliers influence producers’ inventory costs: replenishment lead times and restrictions on order quantities.

Replenishment lead time is the number of days that elapse between inventory reaching or breaching a reorder point and the appearance of replenishment units in stock. Some portion of lead time is internal to the producer, perhaps due to slow reactions in a purchasing department. The rest of lead time is down to the supplier. In this discussion, we assume that suppliers’ contribution to lead times might be changed, for better or for worse. (But the same results could apply to changes in producers’ contributions to lead times.)

The restrictions on order quantities that we consider are order minima and order multiples. You might want to order 3 units of some item, but the supplier might impose a minimum order size of 6 units, so your 3 unit order would have to become a 6 unit order. Or you might want to order 21 units, handily exceeding the minimum order size of 6 units, but if the supplier also has an order multiple of 6, meaning every order must be a multiple of 6 units, then your 21 unit order would have to be increased to 24 units.

Scenario Analyses

To illustrate the use of inventory optimization software for what-if analysis, we examine two sets of scenarios. In the first set, lead times are varied from -20% to +20% of their values in a baseline scenario. In the second set, results are computed first with no supplier restrictions, then with order minima only, and finally with a combination of order minima and order multiples. We use Smart Inventory Optimization software for the calculations.

The baseline scenario uses real-world data on 2,852 spare parts managed by a progressive public transit agency. These parts have an extremely heterogeneous mix of attributes. Their per unit costs range from $1 to $23,105, and their lead times vary between 1 day and 300 days. Over 24 months, the mean demand ranged from less than 1 unit per month to 1,508 units per month, with coefficients of variation ranging from a manageable 10% to a scary 2,171%. Furthermore, the supplier picture is also very complex, involving 293 unique vendors, supplying an average of about 10 parts each. This heterogeneity implies that a real-world optimization would pick and choose among items and vendors. However, for simplicity of exposition and to develop basic insights, our what-if scenarios in this example treat every item and vendor equally. Similarly, we assumed in the baseline that holding costs equaled 20% of the dollar value of an item and that every replenishment order had a fixed cost of $40.

We conducted two what-if experiments. The first examined the effects of changing lead times. The second examined the effects of introducing restrictions on order quantities. In each experiment, we recorded the effects of the changes on two operational metrics: average number of units in stock and average number of orders per year. In turn, these influenced four financial metrics: average dollar value of inventory, average holding cost, average ordering cost, and the sum of the last two, which is total inventory operating cost.

In all scenarios, reorder points were calculated so as to achieve 95% probability of avoiding stockouts while waiting for replenishment. Order quantities, in the absence of supplier restrictions, were computed as what we call “feasible EOQ”. EOQ is the classic “economic order quantity” taught in Inventory 101; it is computed from average demand, holding cost and ordering cost. Feasible EOQ adds an additional consideration: inventory dynamics. If the reorder point is very low, it is possible for EOQ to be too small to sustain a stable, positive level of inventory. In these cases, feasible EOQ increases the order quantity above the EOQ to insure that average inventory does not go negative.

Effects of Changing Lead Times

Table 1 shows the results of changing the lead times. Working around the base case, we changed every item’s lead time by -20%, -10%, +10% and +20%.

It is no surprise that reducing lead times reduced the required level of inventory and increasing them did the opposite. Both the average number of units and the associated dollar value behaved as expected. What may be surprising is that the effects were somewhat muted, i.e., an X percent change in lead time produced a less-than-X percent response. For instance, a 20% reduction in lead time produced only a 7.9% reduction in on-hand inventory and only a 12.0% reduction in the dollar value of those units. Furthermore, the effects of reductions and increases are asymmetric: a 20% increase in lead time led to just a 7.3% increase in units (vs 7.9%) and only a 9.6% increase in inventory value (vs 12.0%).

Similar attenuated and asymmetric results held for operating costs. A 20% reduction in lead time decreased total operating costs by 7.0%, but a 20% increase in lead time caused only a 5.1% increase in operating costs.

Now consider the implications of these results for practice. In a competitive world, cost reductions on the order of 10% or even 5% are significant. This means that efforts to reduce lead times can have important payoffs. In turn, this means that efforts to streamline purchasing processes may be worth doing. Likewise, there is a case for engaging suppliers about reducing their part of lead time, possibly by sharing the savings to incentive them.

Inventory Optimization - Effects of Changing Lead Times
Table 1: Effects of changing lead times

Effect of Order Quantity Restrictions

Table 2 shows the effect of imposing supplier restrictions on order quantities. In the base case, there are no restrictions, i.e., the order minimum is 0 and the order multiple is 1, implying that any order quantity is acceptable to suppliers. Working away from the base case, we first looked at imposing an order minimum of 5 units on all items, then adding an order multiple of 5 for all items.

Forcing orders to be larger than they otherwise would be had the expected impact on the average number of units on hand, increasing it by 0.9% with only an order minimum and by 3.4% with both a minimum and a multiple. The corresponding changes in the dollar value of the inventory were more dramatic: 22.4% and 23.3%. This difference in the size of the percentage response probably traces back to the large number of low-volume/high-cost replacement parts managed by the public transit agency.

Another surprise was the net reduction in operating costs when supplier restrictions were imposed. While holding costs went up by 22.4% and 23.3% in the two what-if scenarios, the larger order quantities allowed for fewer orders per year, resulting in offsetting reductions in ordering costs of, respectively, -24.4% and -32.7%. The net impacts on operating costs were then reductions of 3.7% and 7.9%.

In general, placing restrictions on producer actions would be expected to reduce performance. So the results in these scenarios were counter-intuitive. However, the real message here is that using EOQ, or even enhanced EOQ, to set an order quantity does not give optimum results. Paradoxically, the order quantity restrictions we investigated seem to have forced order quantities closer to optimal levels.

Inventory Optimization - Effect of Order Quantity Restrictions
Table 2: Effect of order quantity restrictions

Conclusions

The what-if analyses shown here do not lead to universal conclusions. For instance, changing the assumed cost per order from $40 to some smaller number could show that the supplier restrictions increased rather than decreased the producer’s inventory operating costs.

When doing what-if analysis in real-word situations, users would naturally craft scenarios at a lower level of detail. For instance, they might evaluate the effect of changes in supplier lead times on a supplier-by-supplier basis to find the ones that would have the highest potential payoffs. Or they might arrange for order minima, if they exist already for all items, to change by a specified percentage instead of a fixed amount, which might be somewhat more realistic.

The key takeaway is that inventory optimization software can be used in “what-if mode” to explore strategic issues, beyond its customary use to calculate reorder points, safety stocks, order quantities, and inventory transfers.

Leave a Comment

Smart Software’s article has won 1st place in the 2022 Supply Chain Brief MVP Awards Forecasting category!

Smart Software is pleased to announce that our article “Managing Inventory amid Regime Change” has won 1st place in the Forecasting category of the 2022 Supply Chain Brief MVP Awards.

Smart Software to Present at Community Summit North America

Smart Software’s Channel Sales Director and Enterprise Solution Engineer, to present three sessions at this year’s Microsoft Dynamics Community Summit North America event in Orlando, FL.
.

Smart Software to lead a webinar as part of the WERC Solutions Partner Program

Smart Software, will lead a 30-minute webinar as part of the WERC Solutions Partner Program. The presentation will focus on how a leading Electric Utility implemented Smart Inventory Planning and Optimization (Smart IP&O) as part of the company’s strategic supply chain optimization (SCO) initiative.

Recent Posts

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
5 Ways to Improve Supply Chain Decision Speed
The promise of a digital supply chain has transformed how businesses operate. At its core, it can make rapid, data-driven decisions while ensuring quality and efficiency throughout operations. However, it's not just about having access to more data. Organizations need the right tools and platforms to turn that data into actionable insights. This is where decision-making becomes critical, especially in a landscape where new digital supply chain solutions and AI-driven platforms can support you in streamlining many processes within the decision matrix. […]
12 Causes of Overstocking and Practical Solutions
Managing inventory effectively is critical for maintaining a healthy balance sheet and ensuring that resources are optimally allocated. Here is an in-depth exploration of the main causes of overstocking, their implications, and possible solutions. […]
FAQ: Mastering Smart IP&O for Better Inventory Management.
Effective supply chain and inventory management are essential for achieving operational efficiency and customer satisfaction. This blog provides clear and concise answers to some basic and other common questions from our Smart IP&O customers, offering practical insights to overcome typical challenges and enhance your inventory management practices. Focusing on these key areas, we help you transform complex inventory issues into strategic, manageable actions that reduce costs and improve overall performance with Smart IP&O. […]
7 Key Demand Planning Trends Shaping the Future
Demand planning goes beyond simply forecasting product needs; it's about ensuring your business meets customer demands with precision, efficiency, and cost-effectiveness. Latest demand planning technology addresses key challenges like forecast accuracy, inventory management, and market responsiveness. In this blog, we will introduce critical demand planning trends, including data-driven insights, probabilistic forecasting, consensus planning, predictive analytics, scenario modeling, real-time visibility, and multilevel forecasting. These trends will help you stay ahead of the curve, optimize your supply chain, reduce costs, and enhance customer satisfaction, positioning your business for long-term success. […]

Inventory Optimization for Manufacturers, Distributors, and MRO

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
Innovating the OEM Aftermarket with AI-Driven Inventory Optimization
The aftermarket sector provides OEMs with a decisive advantage by offering a steady revenue stream and fostering customer loyalty through the reliable and timely delivery of service parts. However, managing inventory and forecasting demand in the aftermarket is fraught with challenges, including unpredictable demand patterns, vast product ranges, and the necessity for quick turnarounds. Traditional methods often fall short due to the complexity and variability of demand in the aftermarket. The latest technologies can analyze large datasets to predict future demand more accurately and optimize inventory levels, leading to better service and lower costs. […]
Future-Proofing Utilities: Advanced Analytics for Supply Chain Optimization
Utilities in the electrical, natural gas, urban water, and telecommunications fields are all asset-intensive and reliant on physical infrastructure that must be properly maintained, updated, and upgraded over time. Maximizing asset uptime and the reliability of physical infrastructure demands effective inventory management, spare parts forecasting, and supplier management. A utility that executes these processes effectively will outperform its peers, provide better returns for its investors and higher service levels for its customers, while reducing its environmental impact. […]
Centering Act: Spare Parts Timing, Pricing, and Reliability
In this article, we'll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We'll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we'll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we'll explore ways to enhance your service-level-driven inventory plan consistently. […]

Blog Categories

Redefine Exceptions and Fine Tune Planning to Address Uncertainty

The Smart Forecaster

Pursuing best practices in demand planning,

forecasting and inventory optimization

Inventory Planning from the Perspective of a Physicist

In a perfect world, Just in Time (JIT) would be the appropriate solution for inventory management. If you can exactly predict what you need and where you need it and your suppliers can get what you need without delay, then you do not need to maintain much inventory locally. But as the saying goes from famous pugilist Mike Tyson, “everyone has a plan until they get punched in the mouth.” And the latest punch in the mouth for the global supply chain was last week’s Suez Canal Blockage that held up $9.6B in trade costing an estimated $6.7M per minute[1]. Disruptions from these and similar events should be modeled and accounted for in your planning.

The assumption that you can exactly predict the future was apparent in Isaac Newton’s laws. Since the 1920’s with the introduction of quantum physics, uncertainty became fundamental to our understanding of nature. Uncertainty is built into fundamental reality. So too should it be built into Supply and Demand Planning processes. Yet too often, black swan events such as the Suez Canal blockage are often thought of as anomalies and as a result, discounted when planning. It is not enough to look back in hindsight and proclaim that it should have been expected. Something needs to be done about addressing the occurrence of other such events in the future and planning stocking levels accordingly.

We must move beyond the “thin tailed distribution” thinking where extreme outcomes are discounted and plan for “fat tails.” So how do we execute a real-world JIT plan when it comes to planning inventory? To do this, the first step is to estimate the realistic lead time to obtain an item. However, estimation is difficult due to lead time uncertainty. Using actual supplier lead times in your company database and external data, you can develop a distribution of possible future lead times and demands within those lead times. Probabilistic forecasting will allow you to account for disruptions and unusual events by not limiting your estimates to what has been observed solely on your own short-term demand and lead time data. You’ll be able to generate possible outcomes with associated probabilities for each occurrence.

Once you have an estimate of the lead time and demand distribution, you can then specify the service level you need to have for that part. Using solutions such as Smart Inventory Optimization (SIO), you will be able confidently stock based on the targeted stock-out risk with minimal inventory carrying cost. You may also consider letting the solution prescribe optimal service level targets by assessing the costs of additional inventory vs. cost of stockout.

Finally, as I have already noted, we need to accept that we can never eliminate all uncertainty. As a physicist, I have always been intrigued by the fact that, even at the most basic levels of reality as we understand it today, there is still uncertainty. Albert Einstein believed in certainty (determinism) in physical law. If he were an inventory manager, he might have argued for JIT because he believed physical laws should allow perfect predictability. He famously said, “God does not play with dice.” Or could it be possible that the universe we exist in was a “black swan” event in a prior “multi-verse” that produced a particular kind of universe that allowed us to exist.

In inventory planning, as in science, we cannot escape the reality of uncertainty and the impact of unusual events. We must plan accordingly.

[1] https://www.bbc.com/news/business-56559073#:~:text=Looking%20at%20the%20bigger%20picture,0.2%20to%200.4%20percentage%20points.

Leave a Comment

Smart Software’s article has won 1st place in the 2022 Supply Chain Brief MVP Awards Forecasting category!

Smart Software is pleased to announce that our article “Managing Inventory amid Regime Change” has won 1st place in the Forecasting category of the 2022 Supply Chain Brief MVP Awards.

Smart Software to Present at Community Summit North America

Smart Software’s Channel Sales Director and Enterprise Solution Engineer, to present three sessions at this year’s Microsoft Dynamics Community Summit North America event in Orlando, FL.
.

Smart Software to lead a webinar as part of the WERC Solutions Partner Program

Recent Posts

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
5 Ways to Improve Supply Chain Decision Speed
The promise of a digital supply chain has transformed how businesses operate. At its core, it can make rapid, data-driven decisions while ensuring quality and efficiency throughout operations. However, it's not just about having access to more data. Organizations need the right tools and platforms to turn that data into actionable insights. This is where decision-making becomes critical, especially in a landscape where new digital supply chain solutions and AI-driven platforms can support you in streamlining many processes within the decision matrix. […]
12 Causes of Overstocking and Practical Solutions
Managing inventory effectively is critical for maintaining a healthy balance sheet and ensuring that resources are optimally allocated. Here is an in-depth exploration of the main causes of overstocking, their implications, and possible solutions. […]
FAQ: Mastering Smart IP&O for Better Inventory Management.
Effective supply chain and inventory management are essential for achieving operational efficiency and customer satisfaction. This blog provides clear and concise answers to some basic and other common questions from our Smart IP&O customers, offering practical insights to overcome typical challenges and enhance your inventory management practices. Focusing on these key areas, we help you transform complex inventory issues into strategic, manageable actions that reduce costs and improve overall performance with Smart IP&O. […]
7 Key Demand Planning Trends Shaping the Future
Demand planning goes beyond simply forecasting product needs; it's about ensuring your business meets customer demands with precision, efficiency, and cost-effectiveness. Latest demand planning technology addresses key challenges like forecast accuracy, inventory management, and market responsiveness. In this blog, we will introduce critical demand planning trends, including data-driven insights, probabilistic forecasting, consensus planning, predictive analytics, scenario modeling, real-time visibility, and multilevel forecasting. These trends will help you stay ahead of the curve, optimize your supply chain, reduce costs, and enhance customer satisfaction, positioning your business for long-term success. […]

Inventory Optimization for Manufacturers, Distributors, and MRO

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
Innovating the OEM Aftermarket with AI-Driven Inventory Optimization
The aftermarket sector provides OEMs with a decisive advantage by offering a steady revenue stream and fostering customer loyalty through the reliable and timely delivery of service parts. However, managing inventory and forecasting demand in the aftermarket is fraught with challenges, including unpredictable demand patterns, vast product ranges, and the necessity for quick turnarounds. Traditional methods often fall short due to the complexity and variability of demand in the aftermarket. The latest technologies can analyze large datasets to predict future demand more accurately and optimize inventory levels, leading to better service and lower costs. […]
Future-Proofing Utilities: Advanced Analytics for Supply Chain Optimization
Utilities in the electrical, natural gas, urban water, and telecommunications fields are all asset-intensive and reliant on physical infrastructure that must be properly maintained, updated, and upgraded over time. Maximizing asset uptime and the reliability of physical infrastructure demands effective inventory management, spare parts forecasting, and supplier management. A utility that executes these processes effectively will outperform its peers, provide better returns for its investors and higher service levels for its customers, while reducing its environmental impact. […]
Centering Act: Spare Parts Timing, Pricing, and Reliability
In this article, we'll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We'll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we'll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we'll explore ways to enhance your service-level-driven inventory plan consistently. […]

Blog Categories

Gaming Out Your Logistical Response to the Corona Virus

The Smart Forecaster

Pursuing best practices in demand planning,

forecasting and inventory optimization

As the world holds its breathe to see how the new corona virus (2019-nCOV) will play out, we cross our fingers for all those currently in quarantine or under treatment and pray that health authorities around the world will soon get the upper hand.

This short note is about one way your business can develop a plan to adjust to one of the likely fallouts from the virus: sudden increases in the time it takes to get inventory replenishment from suppliers. Supply chains around the world are being disrupted. If this happens to you, how can you react in a systematic way?

Reacting to Longer Lead Times

This is a problem that can be solved using advanced supply chain analytics. Presumably, you may have already used this technology to make good choices for the control parameters used in managing all your inventory items, e.g., values for Min and Max or Reorder Point and Order Quantity. The specific technical question addressed here is how to convert an increase in replenishment lead time to changes in those control parameters.

In general, longer lead times require fatter inventories if you want to maintain a high level of customer service. This general rule translates into larger values of Min and/or Max. How much larger depends critically on what new, longer lead time values will appear and their probabilities of occurring.

While many planning software systems assume a fixed lead time, the reality is that almost all lead times have some degree of randomness. Typically, ignoring that randomness increases stockout risk, so having a good estimate of the probability distribution of lead times is important. In normal times, your transactional data can be used to estimate that relationship. But sudden disruptions like 2019-nCOV create unprecedented situations in which you have to make educated guesses about what new delays you will see and how likely they are. We will assume here that you can imagine some such scenarios and want to figure out how to best respond to them.

An Example using Advanced Software

To illustrate this type of prospective planning, consider a hypothetical example. One item, a spare part, has an established pattern of replenishment lead times, with delays of 5, 10 and 15 days occurring with 15%, 70% and 15% probabilities, respectively. Given this distribution and a random demand averaging one unit every 5 days, values of Min = 5 and Max = 10 do a good job. Figure 1 shows a simulation of 10 years of daily operation under this scenario. Fill rate and service level are high, and stockouts are infrequent.

Now suppose that disruptions in the supply chain create a less favorable distribution of lead time, with a 50:50 mix of 15 and 30 days. Figure 2 shows how badly the current values of Min and Max perform in this new scenario. Fill rate and service level plummet due to frequent stockouts. Operating costs more than triple due to penalties for backorders. Only inventory investment (the average dollar value of stock on the shelf) seems to get better, but this happens only because so often there are backorders with nothing left on the shelf. The shift to longer lead times clearly requires new higher values of Min and Max.

Figure 3 shows how the system performs when the Min is increased from 5 to 10 and the Max from 10 to 15. This change compensates for the longer lead times, restoring the previous high levels of fill rate and service level. Inventory investment is necessarily greater, but operating costs are actually lower than before.

Summary

Changes in normal operating conditions require adjustments in the way inventory items are managed. One such change looming large on this date is the potential impact of the 2019-nCOV Corona virus on supply chains, with anticipated increases in replenishment lead times.

Changes in lead times require changes in inventory control parameters such as Min’s and Max’s. These changes are difficult to make with any confidence using pure guesswork. But with some estimate of the increase in lead times, you can use advanced software to learn how to make these adjustments with some confidence.

This note illustrates this point using simulations of the daily operation of an inventory control system.

Figure 1 Simulation of normal operations using current replenishment lead times, Min and Max

Figure 2 Simulation of abnormal operations using longer lead times and current Min and Max

Figure 3 Simulation of abnormal operations using longer lead times and revised Min and Max

Leave a Comment

The Next Frontier in Supply Chain Analytics

Overcoming Uncertainty with Service and Inventory Optimization Technology

Centering Act: Spare Parts Timing, Pricing, and Reliability

Recent Posts

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
5 Ways to Improve Supply Chain Decision Speed
The promise of a digital supply chain has transformed how businesses operate. At its core, it can make rapid, data-driven decisions while ensuring quality and efficiency throughout operations. However, it's not just about having access to more data. Organizations need the right tools and platforms to turn that data into actionable insights. This is where decision-making becomes critical, especially in a landscape where new digital supply chain solutions and AI-driven platforms can support you in streamlining many processes within the decision matrix. […]
12 Causes of Overstocking and Practical Solutions
Managing inventory effectively is critical for maintaining a healthy balance sheet and ensuring that resources are optimally allocated. Here is an in-depth exploration of the main causes of overstocking, their implications, and possible solutions. […]
FAQ: Mastering Smart IP&O for Better Inventory Management.
Effective supply chain and inventory management are essential for achieving operational efficiency and customer satisfaction. This blog provides clear and concise answers to some basic and other common questions from our Smart IP&O customers, offering practical insights to overcome typical challenges and enhance your inventory management practices. Focusing on these key areas, we help you transform complex inventory issues into strategic, manageable actions that reduce costs and improve overall performance with Smart IP&O. […]
7 Key Demand Planning Trends Shaping the Future
Demand planning goes beyond simply forecasting product needs; it's about ensuring your business meets customer demands with precision, efficiency, and cost-effectiveness. Latest demand planning technology addresses key challenges like forecast accuracy, inventory management, and market responsiveness. In this blog, we will introduce critical demand planning trends, including data-driven insights, probabilistic forecasting, consensus planning, predictive analytics, scenario modeling, real-time visibility, and multilevel forecasting. These trends will help you stay ahead of the curve, optimize your supply chain, reduce costs, and enhance customer satisfaction, positioning your business for long-term success. […]

Inventory Optimization for Manufacturers, Distributors, and MRO

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
Innovating the OEM Aftermarket with AI-Driven Inventory Optimization
The aftermarket sector provides OEMs with a decisive advantage by offering a steady revenue stream and fostering customer loyalty through the reliable and timely delivery of service parts. However, managing inventory and forecasting demand in the aftermarket is fraught with challenges, including unpredictable demand patterns, vast product ranges, and the necessity for quick turnarounds. Traditional methods often fall short due to the complexity and variability of demand in the aftermarket. The latest technologies can analyze large datasets to predict future demand more accurately and optimize inventory levels, leading to better service and lower costs. […]
Future-Proofing Utilities: Advanced Analytics for Supply Chain Optimization
Utilities in the electrical, natural gas, urban water, and telecommunications fields are all asset-intensive and reliant on physical infrastructure that must be properly maintained, updated, and upgraded over time. Maximizing asset uptime and the reliability of physical infrastructure demands effective inventory management, spare parts forecasting, and supplier management. A utility that executes these processes effectively will outperform its peers, provide better returns for its investors and higher service levels for its customers, while reducing its environmental impact. […]
Centering Act: Spare Parts Timing, Pricing, and Reliability
In this article, we'll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We'll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we'll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we'll explore ways to enhance your service-level-driven inventory plan consistently. […]

Blog Categories

Logistical Response to the Corona Virus, how to forecast and optimize inventory with high demand and a constant growing

There is a way your business can develop a plan to adjust increasing Demand. Cloud computing companies with unique server and hardware parts, e-commerce, online retailers, home and office supply companies, onsite furniture, power utilities, intensive assets maintenance or warehousing for water supply companies have increased their activity during the pandemic.Delivery service companies, cleaning services, liquor stores and canned or jarred goods warehouses, home improvement stores, gardening suppliers, yard care companies, hardware, kitchen and baking supplies stores, home furniture suppliers with high demand are facing stockouts, long lead times, inventory shortage costs, higher operating costs and ordering costs. Garages selling car parts and truck parts, pharmaceuticals, healthcare or medical supply manufacturers and safety product suppliers are dealing with increasing demand.

If there is a recession, you should …

The Smart Forecaster

Pursuing best practices in demand planning,

forecasting and inventory optimization

Stop buying everything, from paper clips to software? No. You should get a little bit smart about how you are going to ride it out.

Even in normal times, good inventory hygiene suggests that you continuously update your inventory control parameters: reorder points, order quantities, safety stocks, mins, maxes, lead times. Beyond that, you should be updating your inventory strategies, such as adjusting the target service levels or fill rates for every item you hold. That’s the “should.”

But in normal times, it’s easy enough to let those adjustments slide and focus on other things. Then, when the first whiff of recession is in the air, you might get panicky and jump into action in a way that makes it harder to survive the down times. You may look decisive by essentially freezing in place or even shutting some things down, but you risk looking decisive now and foolish later.

Better to take stock of your entire current inventory operation and do that tuning before things get really bad. It is common enough for inventory parameters like reorder points to be set at their current levels by somebody long gone at some time in the distant past for some reason that nobody remembers. Over time, conditions change but the system fails to adapt. So the start of a possible recession is an apt time to run your inventory optimization software to tune up your operations.

You may find that you can remove enough sludge in your current system to offset some or all of the bad news. For instance, your suppliers might be filling orders faster than your software thinks, so you can reduce inventories without risking more stockouts by recalculating reorder points. If you feel you must reduce stocks and ask your customers to accept lower fill rates, you should use your inventory optimization software to identify the best items to put on the chopping block, rather than, say, adjusting every item’s fill rate down by 5%. If you have thousands or tens of thousands of inventory items, that kind of laser-focused adjustment may not be humanly possible without good software support. But with good software support, it’s doable and useful.

Before you hit the panic button, be sure to squeeze all the inefficiency out of your current operations. If, as is common, you have good software but your people are using only a fraction of its capabilities, fix that and get more out of the investment. If you don’t have modern inventory optimization, make a counter-cyclical decision and get some.

If you want to read more about demand planning, forecasting and find new business opportunities in economic recession, read this Journal of Business Forecasting article from the Institute of Business Forecasting (IBF) here or keep reading our new articles

Forklift truck in storage warehouse. Driven by inventory control parameters

Leave a Comment

Recent Posts

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
5 Ways to Improve Supply Chain Decision Speed
The promise of a digital supply chain has transformed how businesses operate. At its core, it can make rapid, data-driven decisions while ensuring quality and efficiency throughout operations. However, it's not just about having access to more data. Organizations need the right tools and platforms to turn that data into actionable insights. This is where decision-making becomes critical, especially in a landscape where new digital supply chain solutions and AI-driven platforms can support you in streamlining many processes within the decision matrix. […]
12 Causes of Overstocking and Practical Solutions
Managing inventory effectively is critical for maintaining a healthy balance sheet and ensuring that resources are optimally allocated. Here is an in-depth exploration of the main causes of overstocking, their implications, and possible solutions. […]
FAQ: Mastering Smart IP&O for Better Inventory Management.
Effective supply chain and inventory management are essential for achieving operational efficiency and customer satisfaction. This blog provides clear and concise answers to some basic and other common questions from our Smart IP&O customers, offering practical insights to overcome typical challenges and enhance your inventory management practices. Focusing on these key areas, we help you transform complex inventory issues into strategic, manageable actions that reduce costs and improve overall performance with Smart IP&O. […]
7 Key Demand Planning Trends Shaping the Future
Demand planning goes beyond simply forecasting product needs; it's about ensuring your business meets customer demands with precision, efficiency, and cost-effectiveness. Latest demand planning technology addresses key challenges like forecast accuracy, inventory management, and market responsiveness. In this blog, we will introduce critical demand planning trends, including data-driven insights, probabilistic forecasting, consensus planning, predictive analytics, scenario modeling, real-time visibility, and multilevel forecasting. These trends will help you stay ahead of the curve, optimize your supply chain, reduce costs, and enhance customer satisfaction, positioning your business for long-term success. […]

Inventory Optimization for Manufacturers, Distributors, and MRO

Managing Spare Parts Inventory: Best Practices
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
Innovating the OEM Aftermarket with AI-Driven Inventory Optimization
The aftermarket sector provides OEMs with a decisive advantage by offering a steady revenue stream and fostering customer loyalty through the reliable and timely delivery of service parts. However, managing inventory and forecasting demand in the aftermarket is fraught with challenges, including unpredictable demand patterns, vast product ranges, and the necessity for quick turnarounds. Traditional methods often fall short due to the complexity and variability of demand in the aftermarket. The latest technologies can analyze large datasets to predict future demand more accurately and optimize inventory levels, leading to better service and lower costs. […]
Future-Proofing Utilities: Advanced Analytics for Supply Chain Optimization
Utilities in the electrical, natural gas, urban water, and telecommunications fields are all asset-intensive and reliant on physical infrastructure that must be properly maintained, updated, and upgraded over time. Maximizing asset uptime and the reliability of physical infrastructure demands effective inventory management, spare parts forecasting, and supplier management. A utility that executes these processes effectively will outperform its peers, provide better returns for its investors and higher service levels for its customers, while reducing its environmental impact. […]
Centering Act: Spare Parts Timing, Pricing, and Reliability
In this article, we'll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We'll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we'll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we'll explore ways to enhance your service-level-driven inventory plan consistently. […]