Two Inventory Problems

If you both make and sell things, you own two inventory problems. Companies that sell things must focus relentlessly on having enough product inventory to meet customer demand.  Manufacturers and asset intensive industries such as power generation, public transportation, mining, and refining, have an additional inventory concern:  having enough spare parts to keep their machines running. This technical brief reviews the basics of two probabilistic models of machine breakdown. It also relates machine uptime to the adequacy of spare parts inventory.

Modeling the failure of a machine treated as a “black box”

Just as product demand is inherently random, so is the timing of machine breakdowns. Likewise, just as probabilistic modeling is the right way to deal with random demand, it is also the right way to deal with random breakdowns.

Models of machine breakdown have two components. The first deals with the random duration of uptime. The second deals with the random duration of downtime.

The field of reliability theory offers several standard probability models describing the random time until failure of a machine without regard for the reason for the failure. The simplest model of uptime is the exponential distribution. This model says that the hazard rate, i.e., the chance of failing in the next instant of time, is constant no matter how long the system has been operating. The exponential model does a good job at modeling certain types of systems, especially electronics, but it is not universally applicable.

Download the Whitepaper

The next step up in model complexity is the Weibull model (pronounced “WHY-bull”). The Weibull distribution allows the risk of failure to change over time, either decreasing after a burn in period or, more often, increasing as wear and tear accumulate. The exponential distribution is a special case of the Weibull distribution in which the hazard rate is neither increasing nor decreasing.

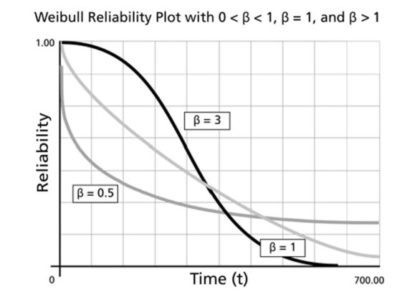
Figure 1: Three different Weibull survival curves

Figure 1 illustrates the Weibull model’s probability that a machine is still running as a function of how long it has been running. There are three curves corresponding to constant, decreasing and increasing hazard rates. For obvious reasons, these are called survival curves because they plot the probability of surviving for various amounts of time (but they are also called reliability curves). The black curve that starts high and sinks fast (β=3) depicts a machine that wears out with age. The lightest curve in the middle fast (β=1) shows the exponential distribution. The medium-dark curve (β=0.5)  is one that has a high early hazard rate but gets better with age.

Of course, there is another phenomenon that needs to be included in the analysis: downtime. Modeling downtime is where inventory theory enters the picture. Downtime is modeled by a mixture of two different distributions. If a spare part is available to replace the failed part, then the downtime can be very brief, say one day. But if there is no spare in stock, then the downtime can be quite long. Even if the spare can be obtained on an expedited basis, it may be several days or a week before the machine can be repaired. If the spare must be fabricated by a far-away supplier and shipped by sea then by rail then trucked to your plant, the downtime could be weeks or months. This all means that keeping a proper inventory of spares is very important to keeping production humming along.

In this aggregated type of analysis, the machine is treated as a black box that is either working or not. Though ignoring the details of which part failed and when, such a model is useful for sizing the pool of machines needed to maintain some minimum level of production capacity with high probability.

The binomial distribution is the probability model relevant to this problem. The binomial is the same model that describes, for example, the distribution of the number of “heads” resulting from twenty tosses of a coin. In the machine reliability problem, the machines correspond to coins, and an outcome of heads corresponds to having a working machine.

As an example, if

• the chance that any given machine is running on any particular day is 90%
• machine failures are independent (e.g., no flood or tornado to wipe them all out at once)
• you require at least a 95% chance that at least 5 machines are running on any given day

then the binomial model prescribes seven machines to achieve your goal.

Modeling machine failures based on component failures

The Weibull model can also be used to describe the failure of a single part. However, any realistically complex production machine will have multiple parts and therefore have multiple failure modes. This means that calculating the time until the machine fails requires analysis of a “race to failure”, with each part vying for the “honor” of being the first to fail.

If we make the reasonable assumption that parts fail independently, standard probability theory points the way to combining the models of individual part failure into an overall model of machine failure. The time until the first of many parts fails has a poly-Weibull distribution. At this point, though, the analysis can get quite complicated, and the best move may be to switch from analysis-by-equation to analysis-by-simulation.

Simulating machine failure from the details of part failures

Simulation analysis got its modern start as a spinoff of the Manhattan Project to build the first atomic bomb. The method is also commonly called Monte Carlo simulation after the biggest gambling center on earth back in the day (today it would be “Macau simulation”).

A simulation model converts the logic of the sequence of random events into corresponding computer code. Then it uses computer-generated (pseudo-)random numbers as fuel to drive the simulation model. For example, each component’s failure time is created by drawing from its particular Weibull failure time distribution. Then the soonest of those failure times begins the next episode of machine downtime.

Figure 2: A simulation of machine uptime over one year of operation

Figure 2 shows the results of a simulation of the uptime of a single machine. Machines cycle through alternating periods of uptime and downtime. In this simulation, uptime is assumed to have an exponential distribution with an average duration (MTBF = Mean Time Before Failure) of 30 days. Downtime has a 50:50 split between 1 day if a spare is available and 30 days if not. In the simulation shown in Figure 2, the machine is working during 85% of the days in one year of operation.

An approximate formula for machine uptime

Although Monte Carlo simulation can provide more exact results, a simpler algebraic model does well as an approximation and makes it easier to see how the key variables relate.

Define the following key variables:

• MTBF = Mean Time Before Failure (days)
• Pa = Probability that there is a spare part available when needed
• MDTshort = Mean Down Time if there is a spare available when needed
• MDTlong = Mean Down Time if there is no spare available when needed
• Uptime = Percentage of days in which the machine is up and running.

Then there is a simple approximation for the Uptime:

Uptime ≈ 100 x MTBF/(MTBF + MDTshort x Pa + MDTlong x (1-Pa)).    (Equation 1)

Equation 1 tells us that the uptime depends on the availability of a spare. If there is always a spare (Pa=1), then uptime achieves a peak value of about 100 x MTBF/(MTBF + MDTshort). If there is never a spare available (Pa=0), then uptime achieve its lowest value of about 100 x MTBF/(MTBF + MDTlong). When the repair time is about as long as the typical time between failures, uptime sinks to an unacceptable level near 50%. If a spare is always available, uptime can approach 100%.

Relating machine downtime to spare parts inventory

Minimizing downtime requires a multi-pronged initiative involving intensive operator training, use of quality raw materials, effective preventive maintenance – and adequate spare parts. The first three set the conditions for good results. The last deals with contingencies.

Once a machine is down, money is flying out the door and there is a premium on getting it back up pronto. This scene could play out in two ways. The good one has a spare part ready to go, so the downtime can be kept to a minimum. The bad one has no available spare, so there is a scramble to expedite delivery of the needed part. In this case, the manufacturer must bear both the cost of lost production and the cost of expedited shipping, if that is even an option.

If the inventory system is properly designed, spare parts availability will not be a major impediment to machine uptime. By the design of an inventory system, I mean the results of several choices: whether the shortage policy is a backorder policy or a loss policy, whether the inventory review cycle is periodic or continuous, and what reorder points and order quantities are established.

When inventory policies for products are designed, they are evaluated using several criteria. Service Level is the percentage of replenishment periods that pass without a stockout. Fill Rate is the percentage of units ordered that is supplied immediately from stock. Average Inventory Level is the typical number of units on hand.

None of these is exactly the metric needed for spare parts stocking, though they all are related. The needed metric is Item Availability, which is the percentage of days in which there is at least one spare ready for use. Higher Service Levels, Fill Rates, and Inventory Levels all imply high Item Availability, and there are ways to convert from one to the other. (When dealing with multiple machines sharing the same stock of spares, Inventory Availability gets replaced by the probability distribution of the number of spares on any given day. We leave that more complex problem for another day.)

Clearly, keeping a good supply of spares reduces the costs of machine downtime. Of course, keeping a good supply of spares creates its own inventory holding and ordering costs. This is the manufacturer’s second inventory problem. As with any decision involving inventory, the key is to strike the right balance between these two competing cost centers. See this article on probabilistic forecasting for intermittent demand for guidance on striking that balance.