Companies that depend on spreadsheets for demand planning, forecasting, and inventory management are often constrained by the spreadsheet’s inherent limitations. This post examines the drawbacks of traditional inventory management approaches caused by spreadsheets and their associated costs, contrasting these with the significant benefits gained from embracing state-of-the-art planning technologies.

Spreadsheets, while flexible for their infinite customizability, are fundamentally manual in nature requiring significant data management, human input, and oversight. This increases the risk of errors, from simple data entry mistakes to complex formula errors, that cause cascading effects that adversely impact forecasts.  Additionally, despite advances in collaborative features that enable multiple users to interact with a common sheet, spreadsheet-based processes are often siloed. The holder of the spreadsheet holds the data.  When this happens, many sources of data truth begin to emerge.  Without the trust of an agreed-upon, pristine, and automatically updated source of data, organizations don’t have the necessary foundation from which predictive modeling, forecasting, and analytics can be built.

In contrast, advanced planning systems like Smart IP&O are designed to overcome these limitations. Such systems are built to automatically ingest data via API or files from ERP and EAM systems, transform that data using built in ETL tools, and can process large volumes of data efficiently.  This enables businesses to manage complex inventory and forecasting tasks with greater accuracy and less manual effort because the data collection, aggregation, and transformation is already done. Transitioning to advanced planning systems is key for optimizing resources for several reasons.

Spreadsheets also have a scaling problem. The bigger the business grows, the greater the number of spreadsheets, workbooks, and formulas becomes.  The result is a tightly wound and rigid set of interdependencies that become unwieldy and inefficient.  Users will struggle to handle the increased load and complexity with slow processing times and an inability to manage large datasets and face challenges collaborating across teams and departments.

On the other hand, advanced planning systems for inventory optimization, demand planning, and inventory management are scalable, designed to grow with the business and adapt to its changing needs. This scalability ensures that companies can continue to manage their inventory and forecasting effectively, regardless of the size or complexity of their operations. By transitioning to systems like Smart IP&O, companies can not only improve the accuracy of their inventory management and forecasting but also gain a competitive edge in the market by being more responsive to changes in demand and more efficient in their operations.

Benefits of Jumping in: An electric utility company struggled to maintain service parts availability without overstocking for over 250,000-part numbers across a diverse network of power generation and distribution facilities. It replaced their twenty-year-old legacy planning process that made heavy use of spreadsheets with Smart IP&O and a real-time integration to their EAM system.  Before Smart, they were only able to modify Min/Max and Safety Stock levels infrequently.  When they did, it was nearly always because a problem occurred that triggered the review.  The methods used to change the stocking parameters relied heavily on gut feel and averages of the historical usage.   The Utility leveraged Smart’s what-if scenarios to create digital twins of alternate stocking policies and simulated how each scenario would perform across key performance indicators such as inventory value, service levels, fill rates, and shortage costs.  The software pinpointed targeted Min/Max increases and decreases that were deployed to their EAM system, driving optimal replenishments of their spare parts.  The result:  A significant inventory reduction of $9 million that freed up cash and valuable warehouse space while sustaining 99%+ target service levels.

Managing Forecast Accuracy: Forecast error is an inevitable part of inventory management, but most businesses don’t track it.  As Peter Drucker said, “You can’t improve what you don’t measure.”  A global high-tech manufacturing company utilizing a spreadsheet-based forecast process had to manually create its baseline forecasts and forecast accuracy reporting.  Given the planners’ workload and siloed processes, they just didn’t update their reports very often, and when they did, the results had to be manually distributed.  The business didn’t have a way of knowing just how accurate a given forecast was and couldn’t cite their actual errors by group of part with any confidence.  They also didn’t know whether their forecasts were outperforming a control method.  After Smart IP&O went live, the Demand Planning module automated this for them. Smart Demand Planner now automatically reforecasts their demand each planning cycle utilizing ML methods and saves accuracy reports for every part x location.  Any overrides that are applied to the forecasts can now be auto-compared to the baseline to measure forecast value add – i.e., whether the additional effort to make those changes improved the accuracy.  Now that the ability to automate the baseline statistical forecasting and produce accuracy reports is in place, this business has solid footing from which to improve their forecast process and resulting forecast accuracy.

Get it Right and Keep it Right:  Another customer in the aftermarket parts business has used Smart’s forecasting solutions since 2005 – nearly 20 years!  They were faced with challenges forecasting intermittently demanded parts sold to support their auto aftermarket business. By replacing their spreadsheet-based approach and manual uploads to SAP with statistical forecasts of demand and safety stock from SmartForecasts, they were able to significantly reduce backorders and lost sales, with fill rates improving from 93% to 96% within just three months.  The key to their success was leveraging Smart’s patented method for forecasting intermittent demand – The “Smart-Willemain” bootstrap method generated accurate estimates of the cumulative demand over the lead time that helped ensure better visibility of the possible demands.

Connecting Forecasts to the Inventory Plan: Advanced planning systems support forecast-based inventory management, which is a proactive approach that relies on demand forecasts and simulations to predict possible outcomes and their associated probabilities.  This data is used to determine optimal inventory levels.  Scenario-based or probabilistic forecasting contrasts with the more reactive nature of spreadsheet-based methods. A longtime customer in the fabric business, previously dealt with overstocks and stockouts due to intermittent demand for thousands of SKUs. They had no way of knowing what their stock-out risks were and so couldn’t proactively modify policies to mitigate risk other than making very rough-cut assumptions that tended to overstock grossly.  They adopted Smart Software’s demand and inventory planning software to generate simulations of demand that identified optimal Minimum On-Hand values and order quantities, maintaining product availability for immediate shipping, highlighting the advantages of a forecast-based inventory management approach.

Better Collaboration:  Sharing forecasts with key suppliers helps to ensure supply.  Kratos Space, part of Kratos Defense & Security Solutions, Inc., leveraged Smart forecasts to provide their Contract Manufacturers with better insights on future demand.  They used the forecasts to make commitments on future buys that enabled the CM to reduce material costs and lead times for engineered-to-order systems. This collaboration demonstrates how advanced forecasting techniques can lead to significant supply chain collaboration that yields efficiencies and cost savings for both parties.

​

In this article, we will review the “suggested orders” functionality in Epicor BisTrack, explain its limitations, and summarize how Smart Inventory Planning & Optimization (Smart IP&O) can help reduce inventory & minimize stock-outs by accurately assessing the tradeoffs between stockout risks and inventory costs.

Automating Replenishment in Epicor BisTrack
Epicor BisTrack’s “Suggested Ordering” can manage replenishment by suggesting what to order and when via reorder point-based policies such as min-max and/or manually specified weeks of supply. BisTrack contains some basic functionality to compute these parameters based on average usage or sales, supplier lead time, and/or user-defined seasonal adjustments. Alternatively, reorder points can be specified completely manually. BisTrack will then present the user with a list of suggested orders by reconciling incoming supply, current on hand, outgoing demand, and stocking policies.

How Epicor BisTrack “Suggested Ordering” Works
To get a list of suggested orders, users specify the methods behind the suggestions, including locations for which to place orders and how to determine the inventory policies that govern when a suggestion is made and in what quantity.

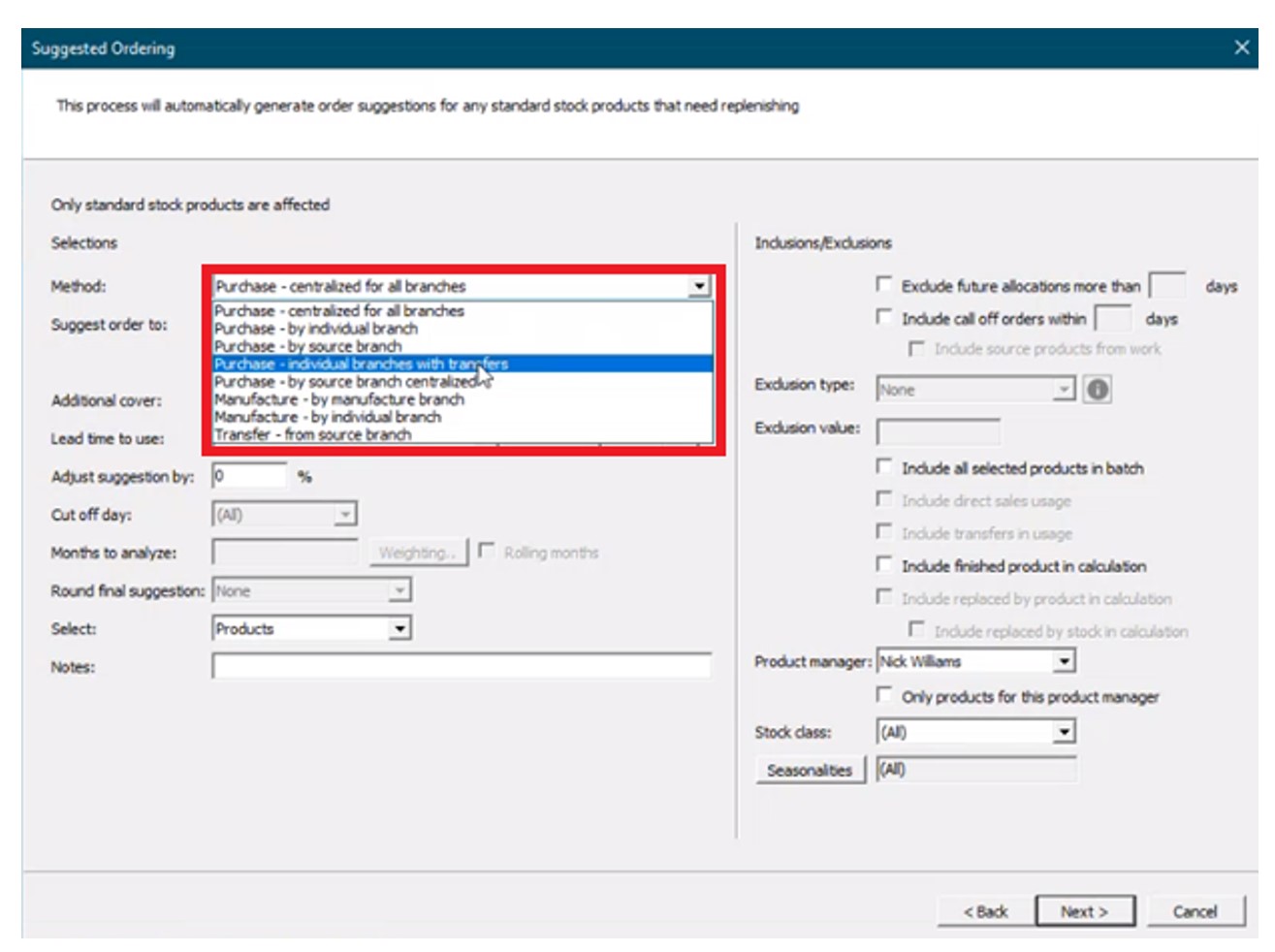
First, the “method” field is specified from the following options to determine what kind of suggestion is generated and for which location(s):

Purchase – Generate purchase order recommendations.

1. Centralized for all branches – Generates suggestions for a single location that buys for all other locations.
2. By individual branch – Generates suggestions for multiple locations (vendors would ship directly to each branch).
3. By source branch – Generates suggestions for a source branch that will transfer material to branches that it services (“hub and spoke”).
4. Individual branches with transfers – Generates suggestions for an individual branch that will transfer material to branches that it services (“hub and spoke”, where the “hub” does not need to be a source branch).

Manufacture – Generate work order suggestions for manufactured goods.

1. By manufacture branch.
2. By individual branch.

Transfer from source branch – Generate transfer suggestions from a given branch to other branches.

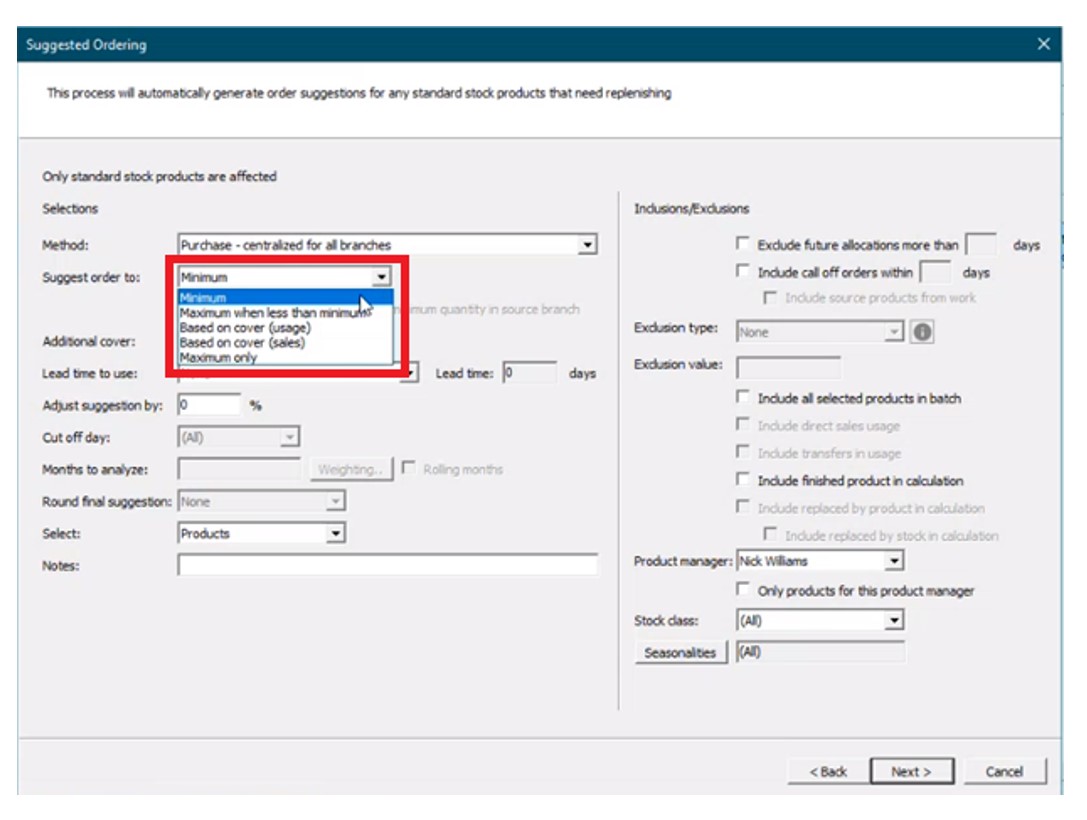
Next, the “suggest order to” is specified from the following options:

1. Minimum – Suggests orders “up to” the minimum on hand quantity (“min”). For any item where supply is less than the min, BisTrack will suggest an order suggestion to replenish up to this quantity.
2. Maximum when less than min – Suggests orders “up to” a maximum on-hand quantity when the minimum on-hand quantity is breached (e.g. a min-max inventory policy).

3. Based on cover (usage) – Suggests orders based on coverage for a user-defined number of weeks of supply with respect to a specified lead time. Given internal usage as demand, BisTrack will recommend orders where supply is less than the desired coverage to cover the difference.

4. Based on over (sales) – Suggests orders based on coverage for a user-defined number of weeks of supply with respect to a specified lead time. Given sales orders as demand, BisTrack will recommend orders where supply is less than the desired coverage to cover the difference.

5. Maximum only – Suggests orders “up to” a maximum on-hand quantity where supply is less than this max.

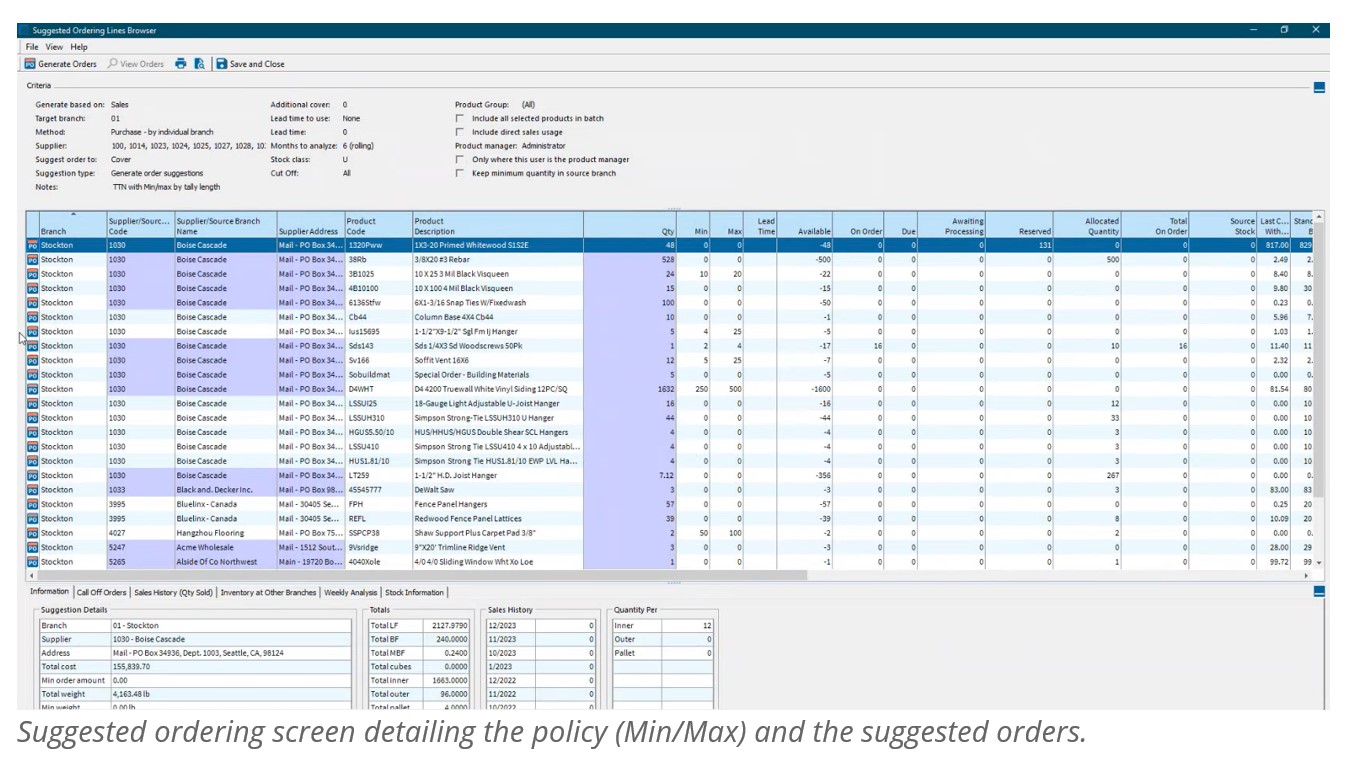
Finally, if allowing BisTrack to determine the reorder thresholds, users can specify additional inventory coverage as buffer stock, lead times, how many months of historical demand to consider, and can also manually define period-by-period weighting schemes to approximate seasonality. The user will be handed a list of suggested orders based on the defined criteria. A buyer can then generate POs for suppliers with the click of a button.

Limitations

Rule-of-thumb Methods

While BisTrack enables organizations to generate reorder points automatically, these methods rely on simple averages that do not capture seasonality, trends, or the volatility in an item’s demand. Averages will always lag behind these patterns and are unable to pick up on trends. Consider a highly seasonal product like a snow shovel—if we take an average of Summer/Fall demand as we approach the Winter season instead of looking ahead, then the recommendations will be based on the slower periods instead of anticipating upcoming demand. Even if we consider an entire years’ worth of history or more, the recommendations will overcompensate during the slower months and underestimate the busy season without manual intervention.

Rule of thumb methods also fail when used to buffer against supply and demand variability.  For example, the average demand over the lead time might be 20 units.  However, a planner would often want to stock more than 20 units to avoid stocking out if lead times are longer than expected or demand is higher than the average.  BisTrack allows users to specify the reorder points based on multiples of the averages.  However, because the multiples don’t account for the level of predictability and variability in the demand, you’ll always overstock predictable items and understock unpredictable ones.   Read this article to learn more about why multiples of the average fail when it comes to developing the right reorder point.

Manual Entry
Speaking of seasonality referenced earlier, BisTrack does allow the user to approximate it through the use of manually entered “weights” for each period. This forces the user to have to decide what that seasonal pattern looks like—for every item. Even beyond that, the user must dictate how many extra weeks of supply to carry to buffer against stockouts, and must specify what lead time to plan around. Is 2 weeks extra supply enough? Is 3 enough? Or is that too much? There is no way to know without guessing, and what makes sense for one item might not be the right approach for all items.

Intermittent Demand
Many BisTrack customers may consider certain items “unforecastable” because of the intermittent or “lumpy” nature of their demand. In other words, items that are characterized by sporadic demand, large spikes in demand, and periods of little or no demand at all. Traditional methods—and rule-of-thumb approaches especially—won’t work for these kinds of items. For example, 2 extra weeks of supply for a highly predictable, stable item might be way too much; for an item with highly volatile demand, this same rule might not be enough. Without a reliable way to objectively assess this volatility for each item, buyers are left guessing when to buy and how much.

Reverting to Spreadsheets
The reality is most BisTrack users tend to do the bulk of their planning off-line, in Excel. Spreadsheets aren’t purpose-built for forecasting and inventory optimization. Users will often bake in user-defined rule of thumb methods that often do more harm than good.  Once calculated, users must input the information back into BisTrack manually. The time consuming nature of the process leads companies to infrequently compute their inventory policies – Many months and on occasion years go by in between mass updates leading to a “set it and forget it” reactive approach, where the only time a buyer/planner reviews inventory policy is at the time of order.  When policies are reviewed after the order point is already breached, it is too late.  When the order point is deemed too high, manual interrogation is required to review history, calculate forecasts, assess buffer positions, and to recalibrate.  The sheer volume of orders means that buyers will just release orders rather than take the painstaking time to review everything, leading to significant excess stock.  If the reorder point is too low, it’s already too late.  An expedite may now be required, driving up costs, assuming the customer doesn’t simply go elsewhere.

Epicor is Smarter
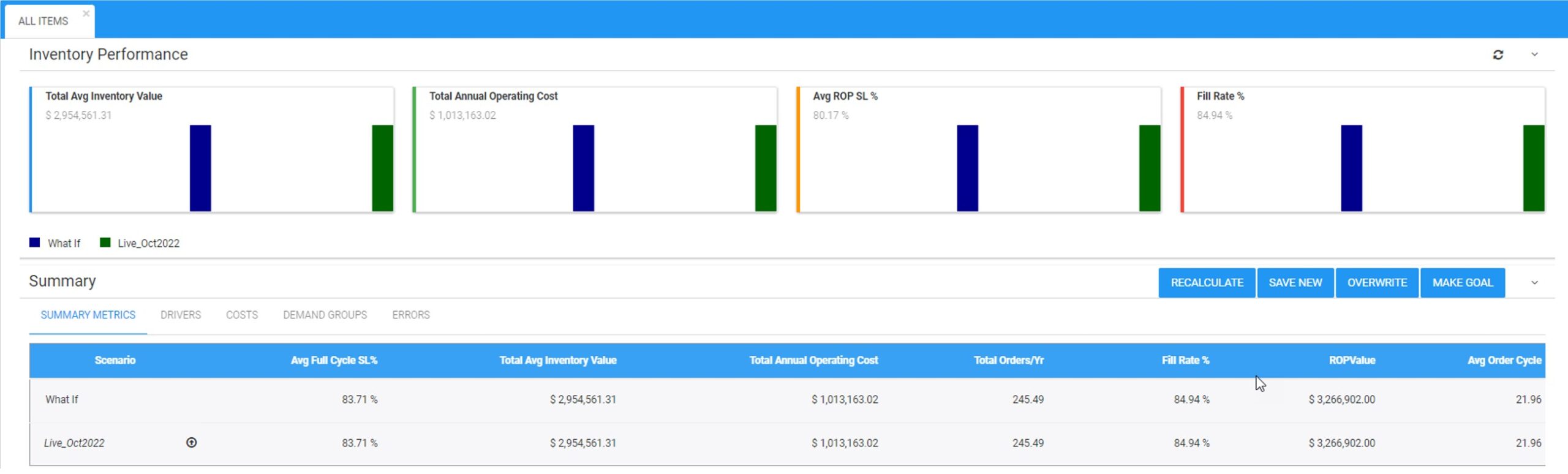
Epicor has partnered with Smart Software and offers Smart IP&O as a cross platform add-on to its ERP solutions including BisTrack, a speciality ERP for the Lumber, hardware, and building material industry.  The Smart IP&O solution comes complete with a bidirectional integration to BisTrack.  This enables Epicor customers to leverage built-for-purpose best of breed inventory optimization applications.  With Epicor Smart IP&O you can generate forecasts that capture trend and seasonality without manual configurations.  You will be able to automatically recalibrate inventory policies using field proven, cutting-edge statistical and probabilistic models that were engineered to accurately plan for intermittent demand.   Safety stocks will accurately account for demand and supply variability, business conditions, and priorities.  You can leverage service level driven planning so you have just enough stock or turn on optimization methods that prescribe the most profitable stocking policies and service levels that consider the real cost of carrying inventory. You can support commodity buys with accurate demand forecasting over longer horizons, and run “what-if” scenarios to assess alternative strategies before execution of the plan.

Smart IP&O customers routinely realize 7 figure annual returns from reduced expedites, increased sales, and less excess stock, all the while gaining a competitive edge by differentiating themselves on improved customer service. To see a recorded webinar hosted by the Epicor Users Group that profiles Smart’s Demand Planning and Inventory Optimization platform, please register here.

For too many companies, a critical piece of data fact-finding ― the measurement of demand uncertainty ― is handled by simple but inaccurate rules of thumb.  For example, demand planners will often compute safety stock by a user-defined multiple of the forecast or historical average.  Or they may configure their ERP to order more when on hand inventory gets to 2 x the average demand over the lead time for important items and 1.5 x for less important ones. This is a huge mistake with costly consequences.

The choice of multiple ends up being a guessing game.  This is because no human being can compute exactly how much inventory to stock considering all the uncertainties.  Multiples of the average lead time demand are simple to use but you can never know whether the multiple used is too large or too small until it is too late.  And once you know, all the information has changed, so you must guess again and then wait and see how the latest guess turns out.  With each new day, you have new demand, new details on lead times, and the costs may have changed.  Yesterday’s guess, no more matter how educated is no longer relevant today.  Proper inventory planning should be void of inventory and forecast guesswork.  Decisions must be made with incomplete information but guessing is not the way to go.

Knowing how much to buffer requires a fact-based statistical analysis that can accurately answer questions such as:

• How much extra stock is needed to improve service levels by 5%
• What the hit to on-time delivery will be if inventory is reduced by 5%
• What service level target is most profitable.
• How will the stockout risk be impacted by the random lead times we face.

Intuition can’t answer these questions, doesn’t scale across thousands of parts, and is often wrong.  Data, probability math and modern software are much more effective. Winging it is not the path to sustained excellence.

I can’t imagine being an inventory planner in spare parts, distribution, or manufacturing and having to create safety stock levels, reorder points, and order suggestions without using key performance predictions of service levels, fill rates, and inventory costs:

Smart’s Inventory Optimization solution generates out-of-the-box key performance predictions that dynamically simulate how your current stocking policies will perform against possible future demands.  It reports on how often you’ll stock out, the size of the stockouts, the value of your inventory, holding costs, and more.  It lets you proactively identify problems before they occur so you can take corrective action in the short term. You can create what-if scenarios by setting targeted service levels and modifying lead times so you an see the predicted impact of these changes before committing to it.

For example,

• You can see if a proposed move from the current service level of 90% to a targeted service level of 97% is financially advantageous
• You can automatically identify if a different service level target is even more profitable to your business that the proposed target.
• You can see exactly how much you’ll need to increase your reorder points to accommodate a longer lead time.

If you aren’t equipping planners with the right tools, they’ll be forced to set stocking policies, safety stock levels, and create demand forecasts in Excel or with outdated ERP functionality.   Not knowing how policies are predicted to perform will leave your company ill equipped to properly allocate inventory.  Contact us today to learn how we can help!

Inventory Control concerns the management of physical goods, focusing on an accurate and up-to-the-minute count of every item in inventory and where it is located, as well as efficient retrieval of items. Relevant technologies include computer databases, barcoding, Radio Frequency Identification (RFID), and the use of robots for retrieval.

Inventory Management aims to execute the inventory policy defined by the company. Inventory Management is often accomplished using Enterprise Resource Planning (ERP) systems, which generate purchase orders, production orders, and reporting that details current inventory on hand, incoming, and up for order.

Inventory Planning sets operational policy details, such as item-specific reorder points and order quantities, and predicts future demand and supplier lead times. Important components of an inventory planning process include what-if scenarios for netting out on-hand inventory, analyzing how changes to demand, lead times, and stocking policies will impact ordering, as well as managing exceptions and contingencies.

Inventory Optimization utilizes an analytical process that computes values for inventory planning parameters (e.g., reorder points and order quantities) that optimize a numerical goal or “objective function” without violating a numerical constraint. For instance, an objective function might be to achieve the lowest possible inventory operating cost (defined as the sum of inventory holding costs, ordering costs, and shortage costs), and the constraint might be to achieve a fill rate of at least 90%. Using a mathematical model of the inventory system and probability forecasts of item demand, inventory optimization can quickly and automatically suggest how to best manage thousands of inventory items.