Utilities have unique supply chain optimization requirements, primarily ensuring high uptime by keeping all critical machines running continuously. Achieving this involves maintaining a high availability of spare parts to guarantee a consistent, reliable, and safe supply. Additionally, as regulated entities, utilities must also carefully manage and control costs.

Managing supply chains efficiently

To maintain a reliable electricity supply at 99.99%⁺ service levels, for example, utilities must be able to respond quickly to changes in demand in the near term and accurately anticipate future demand. To do so, they must have a well-organized supply chain that allows them to purchase the necessary equipment, materials, and services from the right suppliers at the right time, in the right quantities, and at the right price.

Doing so has become increasingly more challenging in the last 3 years.

• Requirements for safety, reliability, and service delivery are more stringent.
• Supply chain disruptions, unpredictable supplier lead times, intermittent spikes in parts usage have always been problematic, but now they are more the rule than the exception.
• Deregulation in the early 2000’s removed spare parts from the list of directly reimbursed items, forcing utilities to pay for spares directly from revenues[1]
• The constant need for capital combined with aggressively climbing interest rates mean costs are scrutinized more than ever.

As a result, Supply Chain Optimization (SCO) has become an increasingly mission-critical business practice for utilities.  To contend with these challenges, utilities can no longer simply manage their supply chain — they must optimize it.  And to do that, investments in new processes and systems will be required.

[1] Scala et al. “Risk and Spare Parts Inventory in Electric Utilities”. Proceedings of the Industrial Engineering Research Conference.

Inventory Planning and Optimization   

Targeted investments in inventory optimization technology offer a path forward for every utility.  Inventory Optimization solutions should be prioritized because they:

1. Can be implemented in a fraction of the time required for initiatives in other areas, such as warehouse management, supply chain design,  and procurement consolidations. It is not uncommon to start generating benefit after 90 days and to have a full software deployment in less than 180 days.
2. Can generate massive ROI, yielding 20x returns and seven figure financial benefits annually. By better forecasting parts usage, utilities will reduce costs by purchasing only the necessary inventory while controlling the risk of stockouts that lead to downtime and poor service levels.
3. Provide foundational support for other initiatives. A strong supply chain rests on the foundation of solid usage forecasts and inventory purchasing plans.

Using predictive analytics and advanced algorithms, inventory optimization helps utilities maximize service levels and reduce operational costs by optimizing inventory levels for spare parts. For example, an electric utility might use statistical forecasting to predict future parts usage, conduct inventory audits to identify excess inventory, and leverage analytical results to identify where inventory optimization efforts should focus first. By doing this, the utility can ensure that machines are running at optimal levels and reduce the risk of costly delays due to a lack of spares.

By using analytics and data, you can identify which spare parts and equipment are most likely to be needed and order only the necessary items. This helps to ensure that equipment has high up-time. It rewards regular monitoring and adjusting of inventory levels so that when operating conditions change, you can detect the change and adjust accordingly. This implies that planning cycles must operate at a tempo high enough to keep up with changing conditions. Leveraging probabilistic forecasting to recalibrate spares stocking policies for each planning cycle ensures that stocking policies (such as min/max levels) are always up-to-date and reflect the latest parts usage and supplier lead times.

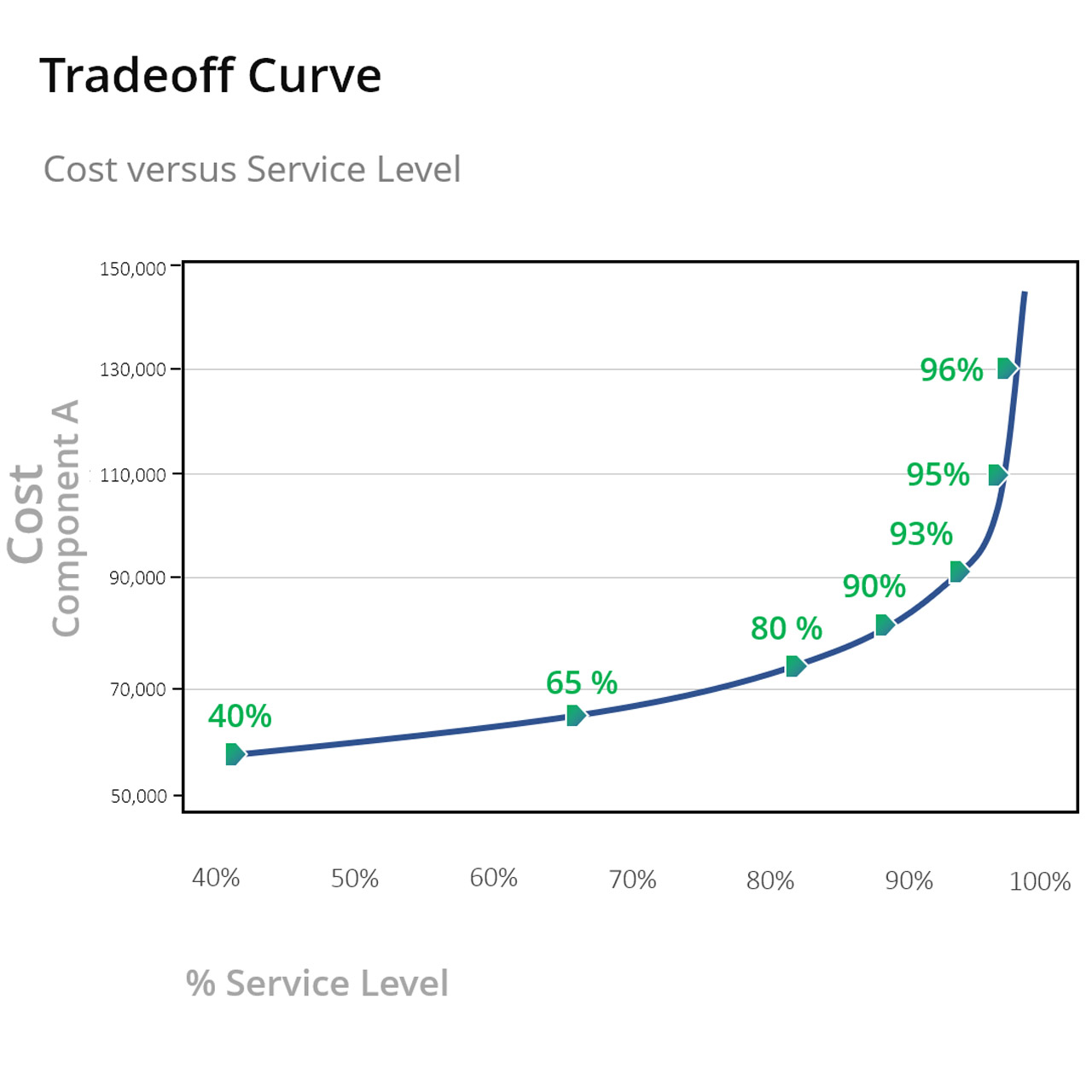
Service Levels and the Tradeoff Curve

The Service Level Tradeoff Curve relates inventory investment to item availability as measured by service level. Service level is the probability that no shortages occur between when you order more stock and when it arrives on the shelf. Surprisingly few companies have data on this important metric across their whole fleet of spare parts.

The Service Level Tradeoff Curve exposes the link between the costs associated with different levels of service and the inventory requirements needed to achieve them.  Knowing which components are important to maintaining high service levels is key to the optimization process and is determined by several factors, including inventory item standardization, criticality, historical usage, and known future repair orders. By understanding this relationship, utilities can better allocate resources, as when using the curves to identify areas where costs can be reduced without hurting system reliability.

With inventory optimization software, setting stocking policies is pure guesswork: It is possible to know how any given increase or decrease will impact service levels other than rough cut estimates.  How the changes will play out in terms of inventory investment, operating costs, and shortage costs, is something no one really knows.  Most utilities rely on rule of thumb methods and arbitrarily adjust stocking policies in a reactive manner after something has gone wrong such as a large stockout or inventory write off.  When adjustments are made this way, there is no fact-based analysis detailing how this change is expected to impact the metrics that matter:  service levels and inventory values.

Inventory Optimization software can compute the detailed, quantitative tradeoff curves required to make informed inventory policy choices or even recommend the target service level that results in the lowest overall operating cost (the sum of holding, ordering, and stock-out costs).  Using this analysis, large increases in stock levels may be mathematically justified when the predicted reduction in shortage costs exceeds the increase in inventory investment and associated holding costs.  By setting appropriate service levels and recalibrating policies across all active parts once every planning cycle (at least once monthly), utilities can minimize the risk of outages while controlling expenditures.

Perhaps the most critical aspects of the response to equipment breakdown are those relating to achieving a first-time fix as rapidly as possible. Having the proper spares available can be the difference between completing a single trip and increasing the mean time to repair, bearing the costs associated with several visits, and causing customer relationships to degrade.

Using modern software, you can benchmark past performance and leverage probabilistic forecasting methods to simulate future performance. By stress-testing your current inventory stocking policies against all plausible scenarios of future parts usage, you will know ahead of time how current and proposed stocking policies are likely to perform. Check out our blog post on how to measure the accuracy of your service level forecast to help you assess the accuracy of inventory recommendations that software providers will purport to provide benefit.

Leveraging Advanced Analytics and AI

When introducing automation, each utility company has its own goals to pursue, but you should begin with assessing present operations to identify areas that may be made more effective. Some companies may prioritize financial issues, but others may prioritize regulatory demands such as clean energy spending or industry-wide changes such as smart grids. Each company’s difficulties are unique, but modern software can point the way to a more effective inventory management system that minimizes excess inventory and places the correct components in the right places at the right times.

Overall, Supply Chain Optimization initiatives are essential for utilities looking to maximize their efficiency and reduce their costs. Technology allows us to make the integration process seamless, and you don’t need to replace your current ERP or EAM system by doing it.  You just need to make better use of the data you already have.

For example, one large utility launched a strategic Supply Chain Optimization (SCO) initiative and added best-in-class capabilities through the selection and integration of commercial off-the-shelf applications.  Chief among these was the Smart Inventory Planning and Optimization system (Smart IP&O), comprising Parts Forecasting / Demand Planning and Inventory Optimization functionality. Within just 90 days the software system was up and running, soon reducing inventory by $9,000,000 while maintaining spares availability at a high level. You can read the case study here Electric Utility Goes with Smart IP&O.

Utilities can ensure that they are able to manage their spare parts supplies in an efficient and cost-effective manner better preparing them for the future.  Over time, this balance between supply and demand translates to a significant edge. Understanding the Service Level Tradeoff Curve helps to understand the costs associated with different levels of service and the inventory requirements needed to achieve them. This leads to reduced operational costs, optimized inventory, and assurance that you can meet your customers’ needs.

In this blog, we are steering the conversation towards the transformative potential of technology in inventory management. The discussion centers around the limitations of simple thinking in managing inventory control processes and the necessity of adopting systematic software solutions. Dr. Tom Willemain highlights the contrast between Smart Software and the basic, albeit comfortable, approaches commonly employed by many businesses. These elementary methods, often favored for their ease of use and zero cost, are scrutinized for their inadequacies in addressing the dynamic challenges of inventory management.

​

​The importance of this subject lies in the critical role inventory management plays in a business’s operational efficiency and its direct impact on customer satisfaction and profitability. Dr. Tom Willemain points out the common pitfalls of relying on oversimplified rules of thumb, such as the whimsical nursery rhyme used by one company to determine reorder points, or the gut feel method, which depends on unquantifiable intuition rather than data. These approaches, while appealing in their simplicity, fail to adapt to market fluctuations, supplier reliability, or changes in demand, thus posing significant risks to the business. The video also critiques the practice of setting reorder points based on multiples of average demand, highlighting its disregard for demand volatility, a fundamental consideration in inventory theory.

Concluding, the presenter advocates for a more sophisticated, data-driven approach to inventory management. By leveraging advanced software solutions like those offered by Smart Software, businesses can accurately model complex demand patterns and stress-test inventory rules against numerous future scenarios. This scientific method allows for the setting of reorder points that account for real-world variability, thereby minimizing the risk of stockouts and the associated costs. The video emphasizes that while simple heuristics may be tempting for their ease of use, they are inadequate for today’s dynamic market conditions. The presenter encourages viewers to embrace technological solutions that offer professional-grade accuracy and adaptability, ensuring sustainable business success.

Just as the renowned astronomer Copernicus transformed our understanding of astronomy by placing the sun at the center of our universe, today, we invite you to re-center your approach to inventory management. And while not quite as enlightening, this advice will help your company avoid being caught in the gravitational pull of inventory woes—constantly orbiting between stockouts, surplus gravity, and the unexpected cosmic expenses of expediting?

In this article, we’ll walk you through the process of crafting a spare parts inventory plan that prioritizes availability metrics such as service levels and fill rates while ensuring cost efficiency. We’ll focus on an approach to inventory planning called Service Level-Driven Inventory Optimization. Next, we’ll discuss how to determine what parts you should include in your inventory and those that might not be necessary. Lastly, we’ll explore ways to enhance your service-level-driven inventory plan consistently.

In service-oriented businesses, the consequences of stockouts are often very significant.  Achieving high service levels depends on having the right parts at the right time. However, having the right parts isn’t the only factor. Your Supply Chain Team must develop a consensus inventory plan for every part, then continuously update it to reflect real-time changes in demand, supply, and financial priorities.

Managing inventory with Service-level-driven planning combines the ability to plan thousands of items with high-level strategic modeling. This requires addressing core issues facing inventory executives:

• Lack of control over supply and associated lead times.
• Unpredictable intermittent demand.
• Conflicting priorities between maintenance/mechanical teams and Materials Management.
• Reactive “wait and see” approach to planning.
• Misallocated inventory, causing stockouts and excess.
• Lack of trust in systems and processes.

The key to optimal service parts management is to grasp the balance between providing excellent service and controlling costs. To do this, we must compare the costs of stockout with the cost of carrying additional spare parts inventory. The costs of a stockout will be higher for critical or emergency spares, when there is a service level agreement with external customers, for parts used in multiple assets, for parts with longer supplier lead times, and for parts with a single supplier. The cost of inventory may be assessed by considering the unit costs, interest rates, warehouse space that will be consumed, and potential for obsolescence (parts used on a soon-to-be-retired fleet have a higher obsolescence risk, for example).

To arbitrate how much stock should be put on the shelf for each part, it is critical to establish consensus on the desired key metrics that expose the tradeoffs the business must make to achieve the desired KPIs. These KPIs will include Service Levels that tell you how often you meet usage needs without falling short on stock, Fill Rates that tell you what percentage of demand is filled, and Ordering costs detail the expenses incurred when you place and receive replenishment orders. You also have Holding costs, which encompass expenses like obsolescence, taxes, and warehousing, and Shortage costs that pertain to expenses incurred when stockouts happen.

An MRO business or Aftermarket Parts Planning team might desire a 99% service level across all parts – i.e., the minimum stockout risk that they are willing to accept is 1%. But what if the amount of inventory needed to support that service level is too expensive? To make an informed decision on whether there is going to be a return on that additional inventory investment, you’ll need to know the stockout costs and compare that to the inventory costs. To get stockout costs, multiply two key elements: the cost per stockout and the projected number of stockouts. To get inventory value, multiply the units required by the unit cost of each part. Then determine the annual holding costs (typically 25-35% of the unit cost). Choose the option that yields a total lower cost. In other words, if the benefit associated with adding more stock (reduced shortage costs) outweighs the cost (higher inventory holding costs), then go for it. A thorough understanding of these metrics and the associated tradeoffs serves as the compass for decision-making.

Modern software aids in this process by allowing you to simulate a multitude of future scenarios. By doing so, you can assess how well your current inventory stocking strategies are likely to perform in the face of different demand and supply patterns. If anything falls short or goes awry, it’s time to recalibrate your approach, factoring in current data on usage history, supplier lead times, and costs to prevent both stockouts and overstock situations.

Enhance your service-level-driven inventory plan consistently.

In conclusion, it’s crucial to assess your service-level-driven plan continuously. By systematically constructing and refining performance scenarios, you can define key metrics and goals, benchmark expected performance, and automate the calculation of stocking policies for all items. This iterative process involves monitoring, revising, and repeating each planning cycle.

The depth of your analysis within these stocking policies relies on the data at your disposal and the configuration capabilities of your planning system. To achieve optimal outcomes, it’s imperative to maintain ongoing data analysis. This implies that a manual approach to data examination is typically insufficient for the needs of most organizations.

For information on how Smart Software can help you meet your service supply chain goals with service-driven planning and more, visit the following blogs.

–   “Explaining What  Service-Level Means in Your Inventory Optimization Software”  Stocking recommendations can be puzzling, especially when they clash with real-world needs.  In this post, we’ll break down what that 99% service level means and why it’s crucial for managing inventory effectively and keeping customers satisfied in today’s competitive landscape.

–  “Service-Level-Driven Planning for Service Parts Businesses” Service-Level-Driven Service Parts Planning is a four-step process that extends beyond simplified forecasting and rule-of-thumb safety stocks. It provides service parts planners with data-driven, risk-adjusted decision support.

–   “How to Choose a Target Service Level.” This is a strategic decision about inventory risk management, considering current service levels and fill rates, replenishment lead times, and trade-offs between capital, stocking and opportunity costs.  Learn approaches that can help.

–   “The Right Forecast Accuracy Metric for Inventory Planning.”  Just because you set a service level target doesn’t mean you’ll actually achieve it. If you are interested in optimizing stock levels, focus on the accuracy of the service level projection. Learn how.

In this video blog, we explore the integral role that inventory models play in shaping the decision-making processes of professionals across various industries. These models, whether they are tangible computer simulations or intangible mental constructs, serve as critical tools in managing the complexities of modern business environments. The discussion begins with an overview of how these models are utilized to predict outcomes and streamline operations, emphasizing their relevance in a constantly evolving market landscape.

​The discussion further explores how various models distinctly influence strategic decision-making processes. For instance, the mental models professionals develop through experience often guide initial responses to operational challenges. These models are subjective, built from personal insights and past encounters with similar situations, allowing quick, intuitive decision-making. On the other hand, computer-based models provide a more objective framework. They use historical data and algorithmic calculations to forecast future scenarios, offering a quantitative basis for decisions that need to consider multiple variables and potential outcomes. This section highlights specific examples, such as the impact of adjusting order quantities on inventory costs and ordering frequency or the effects of fluctuating lead times on service levels and customer satisfaction.

In conclusion, while mental models provide a framework based on experience and intuition, computer models offer a more detailed and numbers-driven perspective. Combining both types of models allows for a more robust decision-making process, balancing theoretical knowledge with practical experience. This approach enhances the understanding of inventory dynamics and equips professionals with the tools to adapt to changes effectively, ensuring sustainability and competitiveness in their respective fields.

In this video blog, the spotlight is on a critical aspect of inventory management: the analysis and interpretation of inventory data. The focus is specifically on a dataset from a public transit agency detailing spare parts for buses. With over 13,700 parts recorded, the data presents a prime opportunity to delve into the intricacies of inventory operations and identify areas for improvement.

Understanding and addressing anomalies within inventory data is important for several reasons. It not only ensures the efficient operation of inventory systems but also minimizes costs and enhances service quality. This video blog explores four fundamental rules of inventory management and demonstrates, through real-world data, how deviations from these rules can signal underlying issues. By examining aspects such as item cost, lead times, on-hand and on-order units, and the parameters guiding replenishment policies, the video provides a comprehensive overview of the potential challenges and inefficiencies lurking within inventory data. 

We highlight the importance of regular inventory data analysis and how such an analysis can serve as a powerful tool for inventory managers, allowing them to detect and rectify problems before they escalate. Relying on antiquated approaches can lead to inaccuracies, resulting in either excess inventory or unfulfilled customer expectations, which in turn could cause considerable financial repercussions and inefficiencies in operations.

Through a detailed examination of the public transit agency’s dataset, the video blog conveys a clear message: proactive inventory data review is essential for maintaining optimal inventory operations, ensuring that parts are available when needed, and avoiding unnecessary expenditures.

Leveraging advanced predictive analytics tools like Smart Inventory Planning and Optimization will help you control your inventory data. Smart IP&O will show you decisive demand and inventory insights into evolving spare parts demand patterns at every moment, empowering your organization with the information needed for strategic decision-making.