​Demand planning and statistical forecasting software play a pivotal role in effective business management by incorporating features that significantly enhance forecasting accuracy. One key aspect involves the utilization of smoothing-based or extrapolative models, enabling businesses to quickly make predictions based solely on historical data. This foundation rooted in past performance is crucial for understanding trends and patterns, especially in variables like sales or product demand. Forecasting software goes beyond mere data analysis by allowing the blending of professional judgment with statistical forecasts, recognizing that forecasting is not a one-size-fits-all process. This flexibility enables businesses to incorporate human insights and industry knowledge into the forecasting model, ensuring a more nuanced and accurate prediction.

Features such as forecasting multiple items as a group, considering promotion-driven demand, and handling intermittent demand patterns are essential capabilities for businesses dealing with diverse product portfolios and dynamic market conditions.  Proper implementation of these applications empowers businesses with versatile forecasting tools, contributing significantly to informed decision-making and operational efficiency.

Extrapolative models

Our demand forecasting solutions support a variety of forecasting approaches including extrapolative or smoothing-based forecasting models, such as exponential smoothing and moving averages.  The philosophy behind these models is simple: they try to detect, quantify, and project into the future any repeating patterns in the historical data.

  There are two types of patterns that might be found in the historical data:

• Trend
• Seasonality

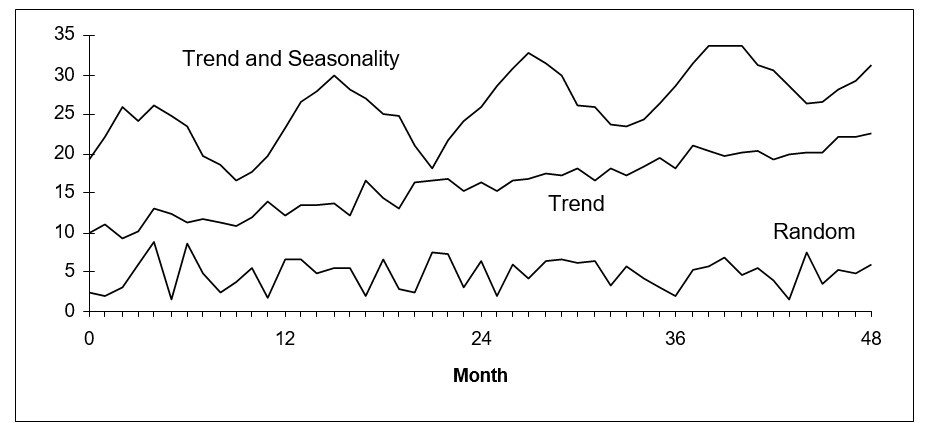
These patterns are illustrated in the following figure along with random data.

Illustrating trending, seasonal, and random time series data

If the pattern is a trend, then extrapolative models such as double exponential smoothing and linear moving average estimates the rate of increase or decrease in the level of the variable and project that rate into the future.

If the pattern is seasonality, then models such as Winters and triple exponential smoothing estimate either seasonal multipliers or seasonal add factors and then apply these to projections of the nonseasonal portion of the data.

Very often, especially with retail sales data, both trend and seasonal patterns are involved. If these patterns are stable, they can be exploited to give very accurate forecasts.

Sometimes, however, there are no obvious patterns, so that plots of the data look like random noise. Sometimes patterns are clearly visible, but they change over time and cannot be relied upon to repeat. In these cases, the extrapolative models don’t try to quantify and project patterns. Instead, they try to average through the noise and make good estimates of the middle of the distribution of data values. These typical values then become the forecasts.  Sometimes, when users see a historical plot with lots of ups and downs they are concerned when the forecast doesn’t replicate those ups and downs. Normally, this should not be a reason for concern.  This occurs when the historical patterns aren’t strong enough to warrant using a forecasting method that would replicate the pattern.  You want to make sure your forecasts don’t suffer from the “wiggle effect” that is described in this blog post.

Past as a predictor of the future

The key assumption implicit in extrapolative models is that the past is a good guide to the future. This assumption, however, can break down. Some of the historical data may be obsolete. For example, the data might describe a business environment that no longer exists. Or, the world that the model represents may be ready to change soon, rendering all the data obsolete. Because of such complicating factors, the risks of extrapolative forecasting are lower when forecasting only a short time into the future.

Extrapolative models have the practical advantage of being cheap and easy to build, maintain and use. They require only accurate records of past values of the variables you need to forecast. As time goes by, you simply add the latest data points to the time series and reforecast. In contrast, the causal models described below require more thinking and more data. The simplicity of extrapolative models is most appreciated when you have a massive forecasting problem, such as making overnight forecasts of demand for all 30,000 items in inventory in a warehouse.

Judgmental adjustments

Extrapolative models can be run in a fully automatic mode with Demand Planner with no intervention required. Causal models require substantive judgment for wise selection of independent variables. However, both types of statistical models can be enhanced by judgmental adjustments. Both can profit from your insights.

Both causal and extrapolative models are built on historical data. However, you may have additional information that is not reflected in the numbers found in the historical record. For instance, you may know that competitive conditions will soon change, perhaps due to price discounts, or industry trends, or the emergence of new competitors, or the announcement of a new generation of your own products. If these events occur during the period for which you are forecasting, they may well spoil the accuracy of purely statistical forecasts. Smart Demand Planner’ graphical adjustment feature lets you include these additional factors in your forecasts through the process of on- screen graphical adjustment.

Be aware that applying user adjustments to the forecast is a two-edged sword. Used appropriately, it can enhance forecast accuracy by exploiting a richer set of information. Used promiscuously, it can add additional noise to the process and reduce accuracy. We advise that you use judgmental adjustments sparingly, but that you never blindly accept the predictions of a purely statistical forecasting method.  It is also very important to measure forecast value add.  That is, the value added to the forecast process by each incremental step.  For example, if you are applying overrides based on business knowledge, it is important to measure whether those adjustments are adding value by improving forecast accuracy.  Smart Demand Planner supports measurement of forecast value add by tracking every forecast considered and automating the forecast accuracy reports. You can select statistical forecasts, measure their errors, and compare them to the overridden ones.  By doing so, you inform the forecasting process so that better decisions can be made in the future. 

Multiple-level forecasts

Another common situation involves multiple-level forecasting, where there are multiple items being forecast as a group or there may even be multiple groups, with each group containing multiple items. We will generally call this type of forecasting Multilevel Forecasting. The prime example is product line forecasting, where each item is a member of a family of items, and the total of all the items in the family is a meaningful quantity.

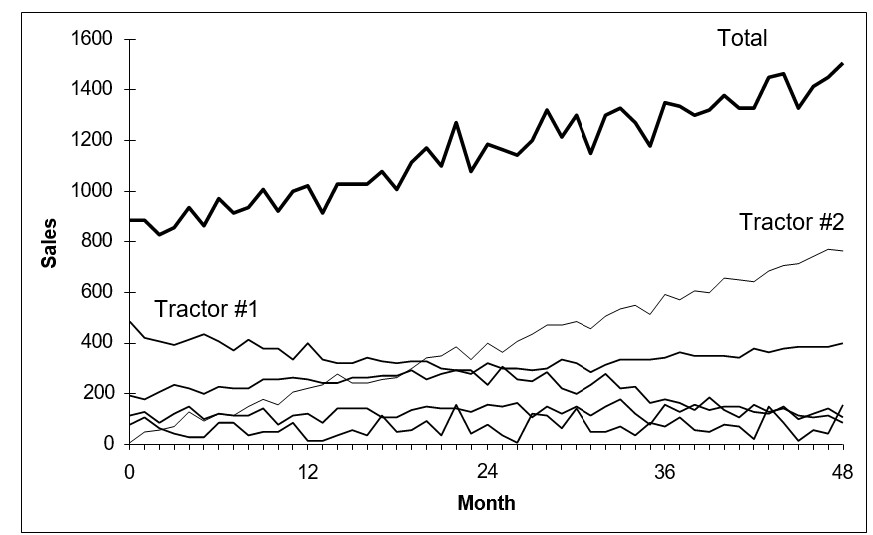
For example, as in the following figure, you might have a line of tractors and want forecasts of sales for each type of tractor and for the entire tractor line.

Illustrating multiple-level product forecasts

 Smart Demand Planner provides Roll Up/Roll Down Forecasting. This function is crucial for obtaining comprehensive forecasts of all product items and their group total. The Roll Down/Roll Up method within this feature offers two options for obtaining these forecasts:

Roll Up (Bottom-Up): This option initially forecasts each item individually and then aggregates the item-level forecasts to generate a family-level forecast.

Roll Down (Top-Down): Alternatively, the roll-down option starts by forming the historical total at the family level, forecasts it, and then proportionally allocates the total down to the item level.

When utilizing Roll Down/Roll Up, you have access to the full array of forecast methods provided by Smart Demand Planner at both the item and family levels. This ensures flexibility and accuracy in forecasting, catering to the specific needs of your business across different hierarchical levels.

Forecasting research has not established clear conditions favoring either the top-down or bottom-up approach to forecasting. However, the bottom-up approach seems preferable when item histories are stable, and the emphasis is on the trends and seasonal patterns of the individual items. Top-down is normally a better choice if some items have very noisy history or the emphasis is on forecasting at the group level. Since Smart Demand Planner makes it fast and easy to try both a bottom-up and a top- down approach, you should try both methods and compare the results.  You can use Smart Demand Planner’s “Hold back on Current”  feature in the “Forecast vs. Actual” to test both approaches on your own data and see which one yields a more accurate forecast for your business. 

For some of our customers, weather has a significant influence on demand. Extreme short-term weather events like fires, droughts, hot spells, and so forth can have a significant near-term influence on demand.

There are two ways to factor weather into a demand forecast: indirectly and directly. The indirect route is easier using the scenario-based approach of Smart Demand Planner. The direct approach requires a tailored special project requiring additional data and hand-crafted modeling.

Indirect Accounting for Weather

The standard model built into Smart Demand Planner (SDP) accommodates weather effects in four ways:

1. If the world is steadily getting warmer/colder/drier/wetter in ways that impact your sales, SDP detects these trends automatically and incorporates them into the demand scenarios it generates.
2. If your business has a regular rhythm in which certain days of the week or certain months of the year have consistently higher or lower-than-average demand, SDP also automatically detects this seasonality and incorporates it into its demand scenarios.
3. Often it is the cussed randomness of weather that interferes with forecast accuracy. We often refer to this effect as “noise”. Noise is a catch-all term that incorporates all kinds of random trouble. Besides weather, a geopolitical flareup, the surprise failure of a regional bank, or a ship getting stuck in the Suez Canal can and have added surprises to product demand. SDP assesses the volatility of demand and reproduces it in its demand scenarios.
4. Management overrides. Most of the time, customers let SDP churn away to automatically generate tens of thousands of demand scenarios. But if users feel the need to touch up specific forecasts using their insider knowledge, SDP can make that happen through management overrides.

Direct Accounting for Weather

Sometimes a user will be able to articulate subject matter expertise linking factors outside their company (such as interest rates or raw materials costs or technology trends) to their own aggregate sales. In these situations, Smart Software can arrange for one-off special projects that provide alternative (“causal”) models to supplement our standard statistical forecasting models. Contact your Smart Software representative to discuss a possible causal modeling project.

Meanwhile, don’t forget your umbrella.

Feynman’s perspective illuminates our journey:  “In its efforts to learn as much as possible about nature, modern physics has found that certain things can never be “known” with certainty. Much of our knowledge must always remain uncertain. The most we can know is in terms of probabilities.” ― Richard Feynman, The Feynman Lectures on Physics.

When we try to understand the complex world of logistics, randomness plays a pivotal role. This introduces an interesting paradox: In a reality where precision and certainty are prized, could the unpredictable nature of supply and demand actually serve as a strategic ally?

The quest for accurate forecasts is not just an academic exercise; it’s a critical component of operational success across numerous industries. For demand planners who must anticipate product demand, the ramifications of getting it right—or wrong—are critical. Hence, recognizing and harnessing the power of randomness isn’t merely a theoretical exercise; it’s a necessity for resilience and adaptability in an ever-changing environment.

Embracing Uncertainty: Dynamic, Stochastic, and Monte Carlo Methods

Dynamic Modeling: The quest for absolute precision in forecasts ignores the intrinsic unpredictability of the world. Traditional forecasting methods, with their rigid frameworks, fall short in accommodating the dynamism of real-world phenomena. By embracing uncertainty, we can pivot towards more agile and dynamic models that incorporate randomness as a fundamental component. Unlike their rigid predecessors, these models are designed to evolve in response to new data, ensuring resilience and adaptability. This paradigm shift from a deterministic to a probabilistic approach enables organizations to navigate uncertainty with greater confidence, making informed decisions even in volatile environments.

Stochastic modeling guides forecasters through the fog of unpredictability with the principles of probability. Far from attempting to eliminate randomness, stochastic models embrace it. These models eschew the notion of a singular, predetermined future, presenting instead an array of possible outcomes, each with its estimated probability. This approach offers a more nuanced and realistic representation of the future, acknowledging the inherent variability of systems and processes. By mapping out a spectrum of potential futures, stochastic modeling equips decision-makers with a comprehensive understanding of uncertainty, enabling strategic planning that is both informed and flexible.

Named after the historical hub of chance and fortune, Monte Carlo simulations harness the power of randomness to explore the vast landscape of possible outcomes. This technique involves the generation of thousands, if not millions, of scenarios through random sampling, each scenario painting a different picture of the future based on the inherent uncertainties of the real world. Decision-makers, armed with insights from Monte Carlo simulations, can gauge the range of possible impacts of their decisions, making it an invaluable tool for risk assessment and strategic planning in uncertain environments.

Real-World Successes: Harnessing Randomness

The strategy of integrating randomness into forecasting has proven invaluable across diverse sectors. For instance, major investment firms and banks constantly rely on stochastic models to cope with the volatile behavior of the stock market. A notable example is how hedge funds employ these models to predict price movements and manage risk, leading to more strategic investment choices.

Similarly, in supply chain management, many companies rely on Monte Carlo simulations to tackle the unpredictability of demand, especially during peak seasons like the holidays. By simulating various scenarios, they can prepare for a range of outcomes, ensuring that they have adequate stock levels without overcommitting resources. This approach minimizes the risk of both stockouts and excess inventory.

These real-world successes highlight the value of integrating randomness into forecasting endeavors. Far from being the adversary it’s often perceived to be, randomness emerges as an indispensable ally in the intricate ballet of forecasting. By adopting methods that honor the inherent uncertainty of the future—bolstered by advanced tools like Smart IP&O—organizations can navigate the unpredictable with confidence and agility. Thus, in the grand scheme of forecasting, it may be wise to embrace the notion that while we cannot control the roll of the dice, we can certainly strategize around it.

In almost every business and industry, decision-makers need reliable forecasts of critical variables, such as sales, revenues, product demand, inventory levels, market share, expenses, and industry trends.

Many kinds of people make these forecasts. Some are sophisticated technical analysts, such as business economists and statisticians. Many others regard forecasting as an important part of their overall work: general managers, production planners, inventory control specialists, financial analysts, strategic planners, market researchers, and product and sales managers. Still, others seldom think of themselves as forecasters but often have to make forecasts on an intuitive, judgmental basis.

Because of the way we designed Smart Demand Planner, it has something to offer all types of forecasters. This design grows out of several observations about the forecasting process. Because we designed Smart Demand Planner with these observations in mind, we believe it has a style and content uniquely suited for turning your browser into an effective forecasting and planning tool:

Forecasting is an art that requires a mix of professional judgment and objective, statistical analysis.

It is often effective to begin with an objective statistical forecast that automatically accounts for trends, seasonality, and other patterns.  Then, apply adjustments or forecast overrides based on your business judgment. Smart Demand Planner makes it easy to execute graphical and tabular adjustments to statistical forecasts.

The forecasting process is usually iterative.

You will likely decide to make several refinements of your initial forecast before you are satisfied. You may want to exclude older historical data that you find to no longer be relevant.  You could apply different weights to the forecast model that put varying emphases on the most recent data. You could apply trend dampening to increase or decrease aggressively trending statistical forecasts.  You could allow the Machine Learning models to fine-tune the forecast selection for you and select the winning model automatically.  Smart Demand Planner’s processing speed gives you plenty of time to make several passes and saves multiple versions of the forecasts as “snapshots” so you can compare forecast accuracy later.

Forecasting requires graphical support.

The patterns evident in data can be seen by a discerning eye. The credibility of your forecasts will often depend heavily on graphical comparisons other business stakeholders make when they assess the historical data and forecasts. Smart Demand Planner provides graphical displays of forecasts, history, and forecast vs. actuals reporting.

Forecasts are never exactly correct.

Because some error always creeps into even the best forecasting process, one of the most useful supplements to a forecast is an honest estimate of its margin of error.

Smart Demand Planner presents both graphical and tabular summaries of forecast accuracy based on the acid test of predicting data held back from development of the forecasting model. 

Forecast intervals or confidence intervals are also very useful.  They detail the likely range of possible demand that is expected to occur.  For example, if actual demand falls outside of the 90% confidence interval more than 10% of the time then there is reason to investigate further.  

Forecasting requires a match of method to data.

One of the major technical tasks in forecasting is to match the choice of forecasting technique to the nature of the data. Features of a data series like trend, seasonality or abrupt shifts in level suggest certain techniques instead of others.

Smart Demand Planner’ Automatic forecasting feature makes this match quickly, accurately and automatically.

Forecasting is often a part of a larger process of planning or control.

For example, forecasting can be a powerful complement to spreadsheet-based financial analysis, extending rows of figures off into the future. In addition, accurate sales and product demand forecasts are fundamental inputs to a manufacturer’s production planning and inventory control processes. An objective statistical forecast of future sales will always help identify when the budget (or sales plan) may be too unrealistic. Gap analysis enables the business to take corrective action to their demand and marketing plans to ensure they do not miss the budgeted plan.

Forecasts need to be integrated into ERP systems
Smart Demand Planner can quickly and easily transfer its results to other applications, such as spreadsheets, databases and planning systems including ERP applications.  Users are able to export forecasts in a variety of file formats either via download or to secure FTP file locations.  Smart Demand Planner includes API based integrations to a variety of ERP and EAM systems including Epicor Kinetic and Epicor Prophet 21, Sage X3 and Sage 300, Oracle NetSuite, and each of Microsoft’s Dynamics 365 ERP systems. API based integrations enable customers to push forecast results directly back to the ERP system on demand.

The result is more efficient sales planning, budgeting, production scheduling, ordering, and inventory planning.

​When you should use traditional extrapolative forecasting techniques.

With so much hype around new Machine Learning (ML) and probabilistic forecasting methods, the traditional “extrapolative” or “time series” statistical forecasting methods seem to be getting the cold shoulder.  However, it is worth remembering that these traditional techniques (such as single and double exponential smoothing, linear and simple moving averaging, and Winters models for seasonal items) often work quite well for higher volume data. Every method is good for what it was designed to do.  Just apply each appropriately, as in don’t bring a knife to a gunfight and don’t use a jackhammer when a simple hand hammer will do. 

Extrapolative methods perform well when demand has high volume and is not too granular (i.e., demand is bucketed monthly or quarterly). They are also very fast and do not use as many computing resources as probabilistic and ML methods. This makes them very accessible.

Are the traditional methods as accurate as newer forecasting methods?  Smart has found that extrapolative methods do very poorly when demand is intermittent. However, when demand is higher volume, they only do slightly worse than our new probabilistic methods when demand is bucketed monthly.  Given their accessibility, speed, and the fact you are going to apply forecast overrides based on business knowledge, the baseline accuracy difference here will not be material.

The advantage of more advanced models like Smart’s GEN2 probabilistic methods is when you need to predict patterns using more granular buckets like daily (or even weekly) data.  This is because probabilistic models can simulate day of the week, week of the month, and month of the year patterns that are going to be lost with simpler techniques.  Have you ever tried to predict daily seasonality with a Winter’s model? Here is a hint: It’s not going to work and requires lots of engineering.

Probabilistic methods also provide value beyond the baseline forecast because they generate scenarios to use in stress-testing inventory control models. This makes them more appropriate for assessing, say, how a change in reorder point will impact stockout probabilities, fill rates, and other KPIs. By simulating thousands of possible demands over many lead times (which are themselves presented in scenario form), you’ll have a much better idea of how your current and proposed stocking policies will perform. You can make better decisions on where to make targeted stock increases and decreases.

So, don’t throw out the old for the new just yet. Just know when you need a hammer and when you need a jackhammer.