Our customers have usually settled into one way to manage their service parts inventory. The professor in me would like to think that the chosen inventory policy was a reasoned choice among considered alternatives, but more likely it just sort of happened. Maybe the inventory honcho from long ago had a favorite and that choice stuck. Maybe somebody used an EAM or ERP system that offered only one choice. Perhaps there were some guesses made, based on the conditions at the time.

The Competitors

Too seldom, businesses make these choices in haphazard ways. But modern service parts planning software lets you be more systematic about your choices. This post demonstrates that proposition by making objective comparisons among three popular inventory policies:  Order Up To, Reorder Point/Order Quantity, and Min/Max.  I discussed each of these policies in this video blog.

• Order Up To. This is a periodic review policy where every T days, on-hand inventory is tallied and an order of random size is placed to bring the stock level back up to S units.
• Q, R or Reorder Point/Order Quantity. Q, R is a continuous review policy where every day, inventory is tallied. If there are Q or fewer units on hand, an order of fixed size is placed for R more units.
• Min, Max is another continuous review policy where every day, inventory is tallied. If there are Min or fewer units on hand, an order is placed to bring the stock level back up to Max units.

Inventory theory says these choices are listed in increasing order of effectiveness. The first option, Order Up To, is clearly the simplest and cheapest to implement, but it closes its eyes to what’s going on for long periods of time.  Imposing a specified passage of time in between orders makes it, in theory, less flexible. In contrast, the two continuous review options keep an eye on what’s happening all the time, so they can react to potential stockouts quicker. The Min/Max option is, in theory, more flexible than the option that uses a fixed reorder quantity because the size of the order dynamically changes to accommodate the demand.

That’s the theory. This post examines evidence from head-to-head comparisons to check the theory and put concrete numbers on the relative performance of the three policies.

The Meaning of “Best”

How should we keep score in this tournament? If you are a regular reader of this Smart Forecaster blog, you know that the core of inventory planning is a tug-of-war between two opposing objectives: keeping inventory lean vs keeping item availability metrics such as service level high.

To simplify things, we will compute “one number to rule them all”: the average operating cost. The winning policy will be the one with the lowest average.

This average is the sum of three components: the cost of holding inventory (“holding cost”), the cost of ordering replenishment units (“ordering cost”) and the cost of losing a sale (“shortage cost”). To make things concrete, we used the following assumptions:

• Each service part is valued at $1,000.
• Annual holding cost is 10% of item value, or $100 per year per unit.
• Processing each replenishment order costs $20 per order.
• Each unit demanded but not provided costs the value of the part, $1,000.

For simplicity, we will refer to the average operating cost as simply “the cost”.

Of course, the lowest average cost can be achieved by getting out of the business. So the competition required a performance constraint on item availability: Each option had to achieve a fill rate of at least 99%.

The Alternatives Duke it Out

A key element of context is whether stockouts result in losses or backorders. Assuming that the service part in question is critical, we assumed that unfilled orders are lost, which means that a competitor fills the order. In an MRO environment, this will mean additional downtime due to stockout.

To compare the alternatives, we used our predictive modeling engine to run a large number of Monte Carlo simulations.  Each simulation involved specifying the parameter values of each policy (e.g., Min and Max values), generating a demand scenario, feeding that into the logic of the policy, and measuring the resulting cost averaged over 365 days of operation. Repeating this process 1,000 times and averaging the 1,000 resulting costs gave the final result for each policy.  

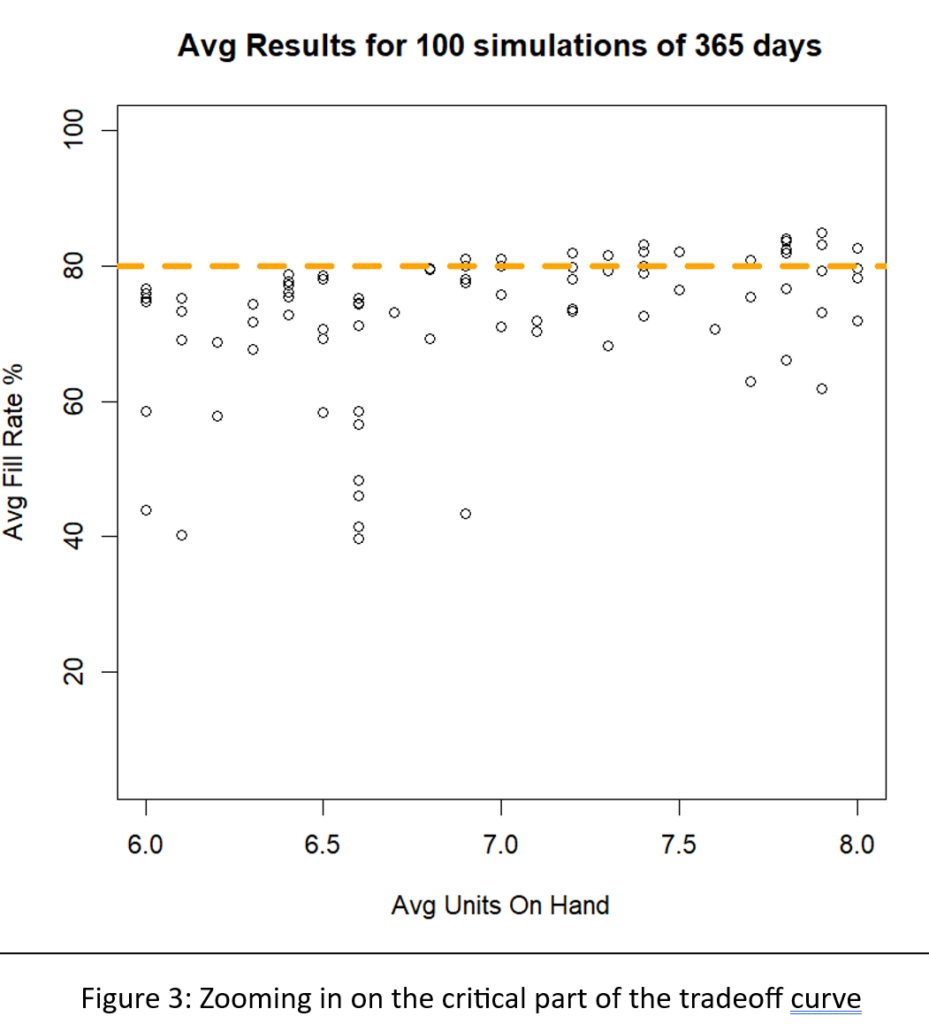
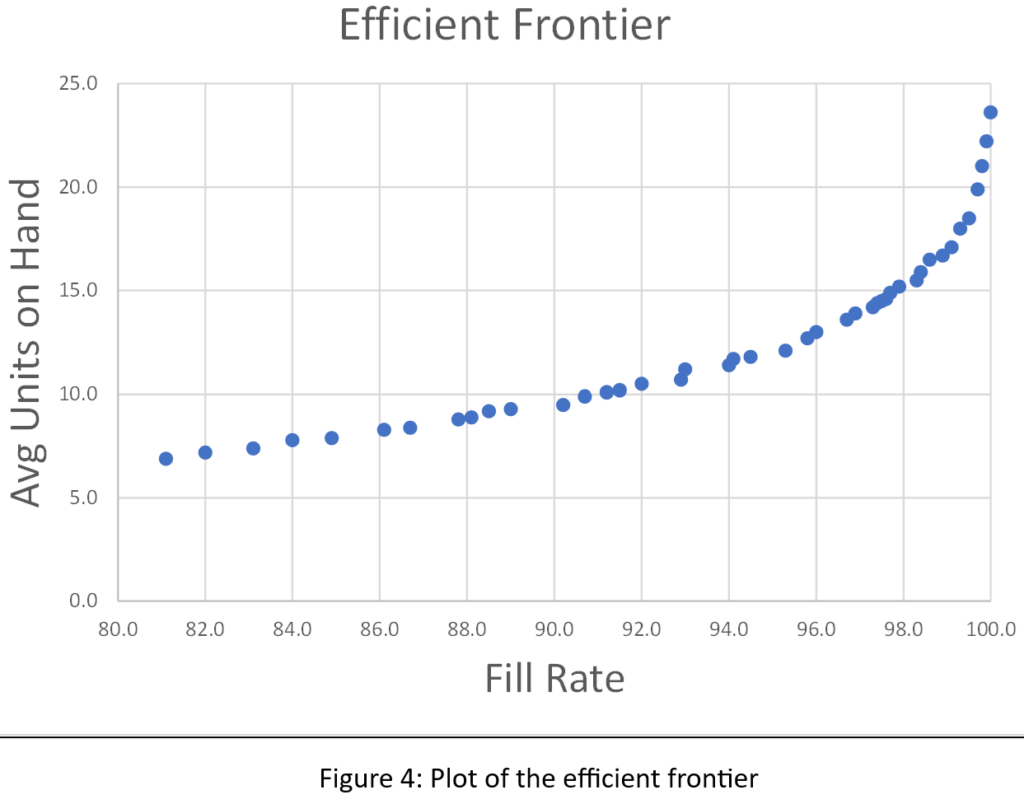
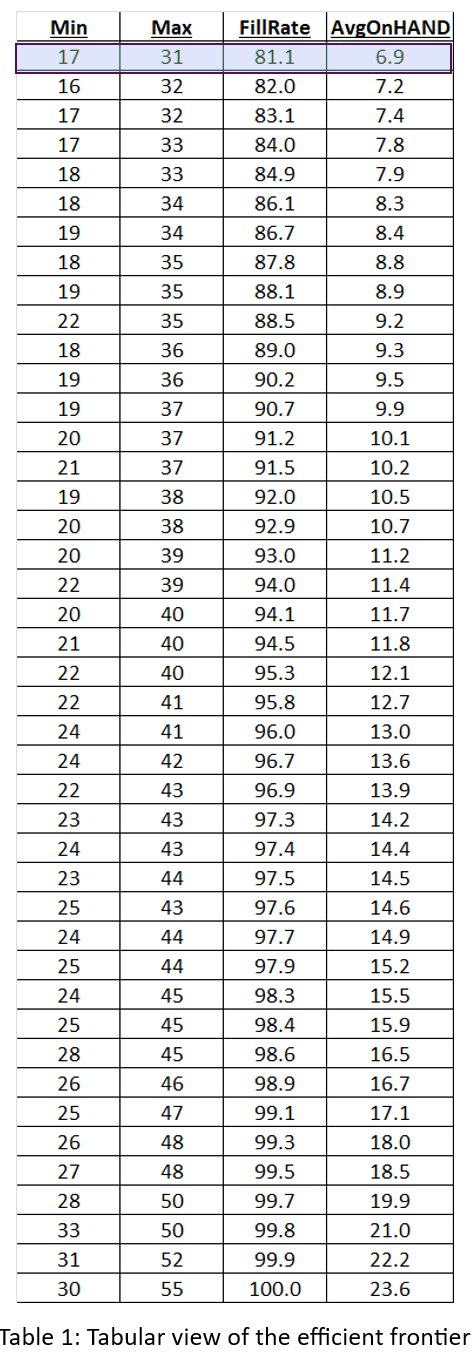
To make the comparison fair, each alternative had to be designed for its best performance. So we searched the “design space” of each policy to find the design with the lowest cost. This required repeating the process described in the previous paragraph for many pairs of parameter values and identifying the pair yielding the lost average annual operating cost.

Using the algorithms in Smart Inventory Optimization (SIO^TM) we made head-to-head-to-head comparisons under the following assumptions about demand and supply:

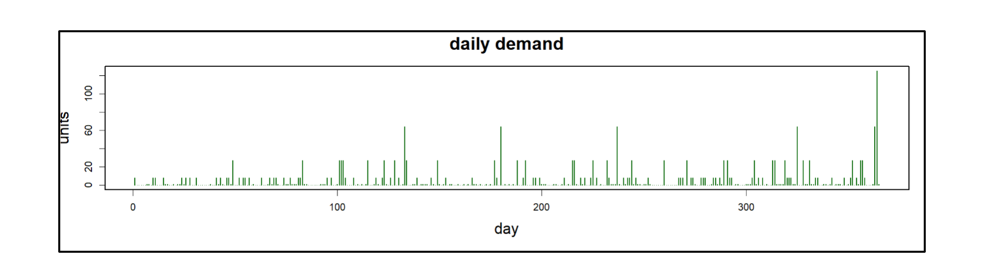
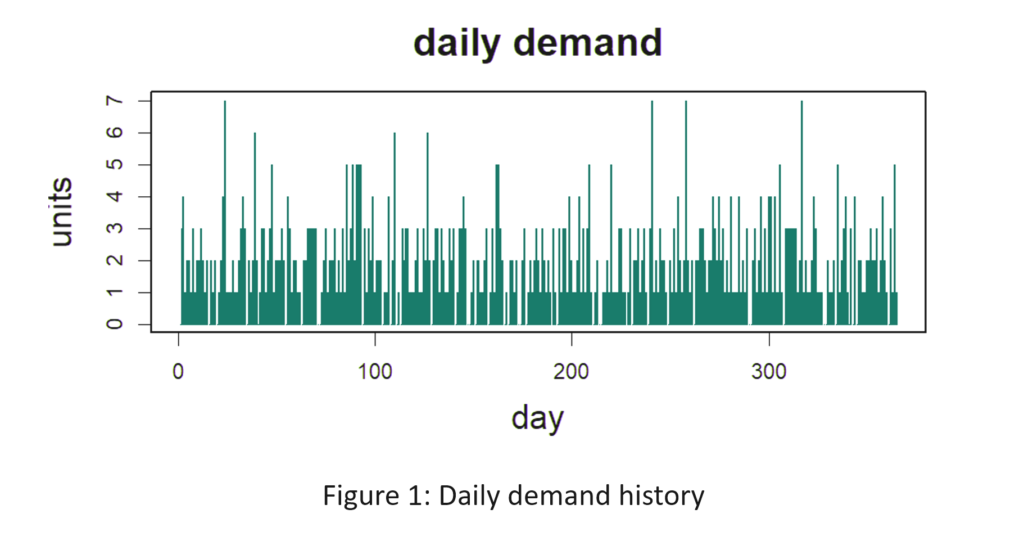
• Item demand was assumed to be intermittent and highly variable but relatively simple in that there was neither trend nor seasonality, as is often true for service parts. Daily mean demand was 5 units with a large standard deviation of 13 units. Figure 1 shows a sample of one year’s demand. We have chosen a very challenging demand pattern, in which some days have 10 to even 20 times the average demand.

Figure 1: Daily part demand was assumed to be intermittent and very spikey.

​​

• Suppliers’ replenishment lead times were 14 days 75% of the time and 21 days otherwise. This reflects the fact that there is always uncertainty in the supply chain.

And the Winner Is…

Was the theory right? Kinda’ sorta’.

Table 1 shows the results of the simulation experiments. For each of the three competing policies, it shows the average annual operating cost, the margin of error (technically, an approximate 95% confidence interval for the mean cost), and the apparent best choices for parameter values.

Table 1: Results of the simulated comparisons

For example, the average cost for the (T,S) policy when T is fixed at 30 days was $41,680. But the Plus/Minus implies that the results are compatible with a “true” cost (i.e., the estimate from an infinite number of simulations) of anywhere between $39,890 and $43,650. The reason there is so much statistical uncertainty is the extremely spikey nature of demand in this example.

Table 1 says that, in this example, the three policies fall in line with expectations. However, more useful conclusions would be:

1. The three policies are remarkably similar in average cost. By clever choice of parameter values, one can get good results out of any of the three policies.
2. Not shown in Table 1, but clear from the detailed simulation results, is that poor choices for parameter values can be disastrous for any policy.
3. It is worth noting that the periodic review (T,S) policy was not allowed to optimize over possible values of T. We fixed T at 30 to mimic what is common in practice, but those who use the periodic review policy should consider other review periods. An additional experiment fixed the review period at T = 7 days. The average cost in this scenario was minimized at $36,551 ± $1,668 with S = 343. This result is better than that using T = 30 days.
4. We should be careful about over-generalizing these results. They depend on the assumed values of the three cost parameters (holding, ordering and shortage) and the character of the demand process.
5. It is possible to run experiments like those shown here automatically in Smart Inventory Optimization. This means that you too would be able to explore design choices in a rigorous way.

Some companies invest in software to help them manage their inventory, whether it’s spare parts or finished goods. But a surprising number of others play the Inventory Guessing Game every day, trusting to an imagined “Golden Gut” or to plain luck to set their inventory control parameters. But what kind of results do you expect with that approach?

How good are you at intuiting the right values? This blog post challenges you to guess the best Min and Max values for a notional inventory item. We’ll show you its demand history, give you a few relevant facts, then you can pick Min and Max values and see how well they would work. Ready?

The Challenge

Figure 1 shows the daily demand history of the item. The average demand is 2 units per day. Replenishment lead time is a constant 10 days (which is unrealistic but works in your favor). Orders that cannot be filled immediately from stock cannot be backordered and are lost. You want to achieve at least an 80% fill rate, but not at any cost. You also want to minimize the average number of units on hand while still achieving at least an 80% fill rate. What Min and Max values would produce an 80% fill rate with the lowest average number of units on hand? [Record your answers for checking later. The solution appears below at the end of the article.]

Computing the Best Min and Max Values

The way to determine the best values is to use a digital twin, also known as a Monte Carlo simulation. The analysis creates a multitude of demand scenarios and passes them through the mathematical logic of the inventory control system to see what values will be taken on by key performance indicators (KPI’s).

We built a digital twin for this problem and systematically exercised it with 1,085 pairs of Min and Max values. For each pair, we simulated 365 days of operation a total of 100 times. Then we averaged the results to assess the performance of the Min/Max pair in terms of two KPI’s: fill rate and average on hand inventory.

Figure 2 shows the results. The inherent tradeoff between inventory size and fill rate is clear in the figure: if you want a higher fill rate, you have to accept a larger inventory. However, at each level of inventory there is a range of fill rates, so the game is to find the Min/Max pair that yields the highest fill rate for any given size inventory.

A different way to interpret Figure 2 is to focus on the dashed green line marking the target 80% fill rate. There are many Min/Max pairs that can hit near the 80% target, but they differ in inventory size from about 6 to about 8 units. Figure 3 zooms in on that region of Figure 2 to show  quite a number of Min/Max pairs that are competitive.

We sorted the results of all 1,085 simulations to identify what economists call the efficient frontier. The efficient frontier is the set of most efficient Min/Max pairs to exploit the tradeoff between fill rate and units on hand. That is, it is a list of Min/Max pairs that provide the least cost way to achieve any desired fill rate, not just 80%. Figure 4 shows the efficient frontier for this problem. Moving from left to right, you can read off the lowest price you would have to pay (as measured by average inventory size) to achieve any target fill rate. For example, to achieve a 90% fill rate, you would have to carry an average inventory of about 10 units.

Figures 2, 3, and 4 show results for various Min/Max pairs but do not display the values of Min and Max behind each point. Table 1 displays all the simulation data: the values of Min, Max, average units on hand and fill rate. The answer to the guessing game is highlighted in the first line of the table: Min=7 and Max=13¹. Did you get the right answer, or something close²? Did you maybe get onto the efficient frontier?

Conclusions

Maybe you got lucky, or maybe you do indeed have a Golden Gut, but it’s more likely you didn’t get the right answer, and it’s even more likely you didn’t even try. Figuring out the right answer is extremely difficult without using the digital twin. Guessing is unprofessional.

One step up from guessing is “guess and see”, in which you implement your guess and then wait a while (months?) to see if you like the results. That tactic is at least “scientific”, but it is inefficient.

Now consider the effort to work out the best (Min,Max) pairs for thousands of items. At that scale, there is even less justification for playing the Inventory Guessing Game. The right answer is to play it… Smart³.

¹ This answer has a bonus, in that it achieves a bit more than 80% fill rate at a lower average inventory size than the Min/Max combination that hit exactly 80%. In other words, (7,13) is on the efficient frontier.

² Because these results come from a simulation instead of an exact mathematical equation, there is a certain margin of error associated with each estimated fill rate and inventory level. However, because the average results were based on 100 simulations each 365 days long, the margins of error are small. Across all experiments, the average standard errors in fill rate and mean inventory were, respectively, only 0.009% and 0.129 units.

³ In case you didn’t know this, one of the founders of Smart Software was … Charlie Smart.