Some companies invest in software to help them manage their inventory, whether it’s spare parts or finished goods. But a surprising number of others play the Inventory Guessing Game every day, trusting to an imagined “Golden Gut” or to plain luck to set their inventory control parameters. But what kind of results do you expect with that approach?

How good are you at intuiting the right values? This blog post challenges you to guess the best Min and Max values for a notional inventory item. We’ll show you its demand history, give you a few relevant facts, then you can pick Min and Max values and see how well they would work. Ready?

The Challenge

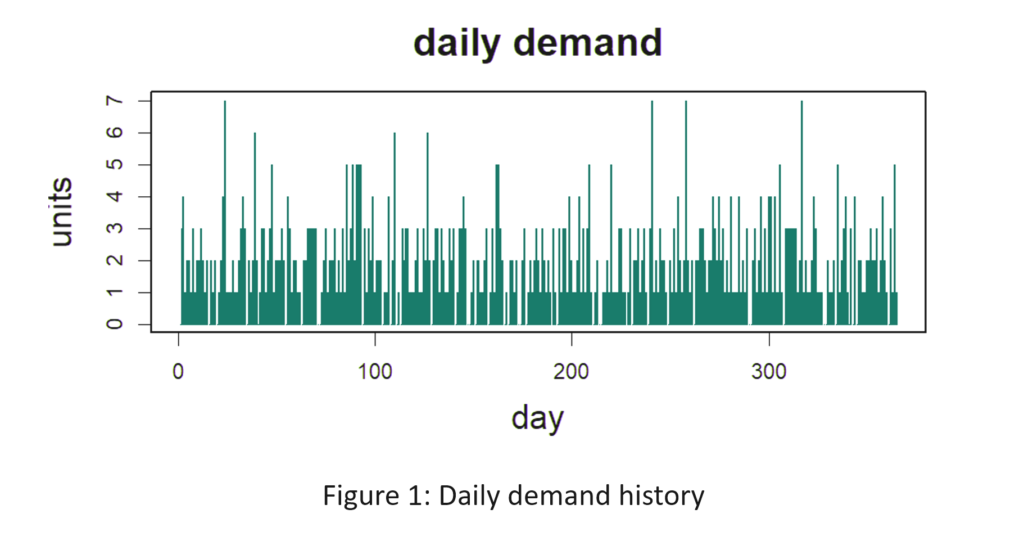
Figure 1 shows the daily demand history of the item. The average demand is 2 units per day. Replenishment lead time is a constant 10 days (which is unrealistic but works in your favor). Orders that cannot be filled immediately from stock cannot be backordered and are lost. You want to achieve at least an 80% fill rate, but not at any cost. You also want to minimize the average number of units on hand while still achieving at least an 80% fill rate. What Min and Max values would produce an 80% fill rate with the lowest average number of units on hand? [Record your answers for checking later. The solution appears below at the end of the article.]

Computing the Best Min and Max Values

The way to determine the best values is to use a digital twin, also known as a Monte Carlo simulation. The analysis creates a multitude of demand scenarios and passes them through the mathematical logic of the inventory control system to see what values will be taken on by key performance indicators (KPI’s).

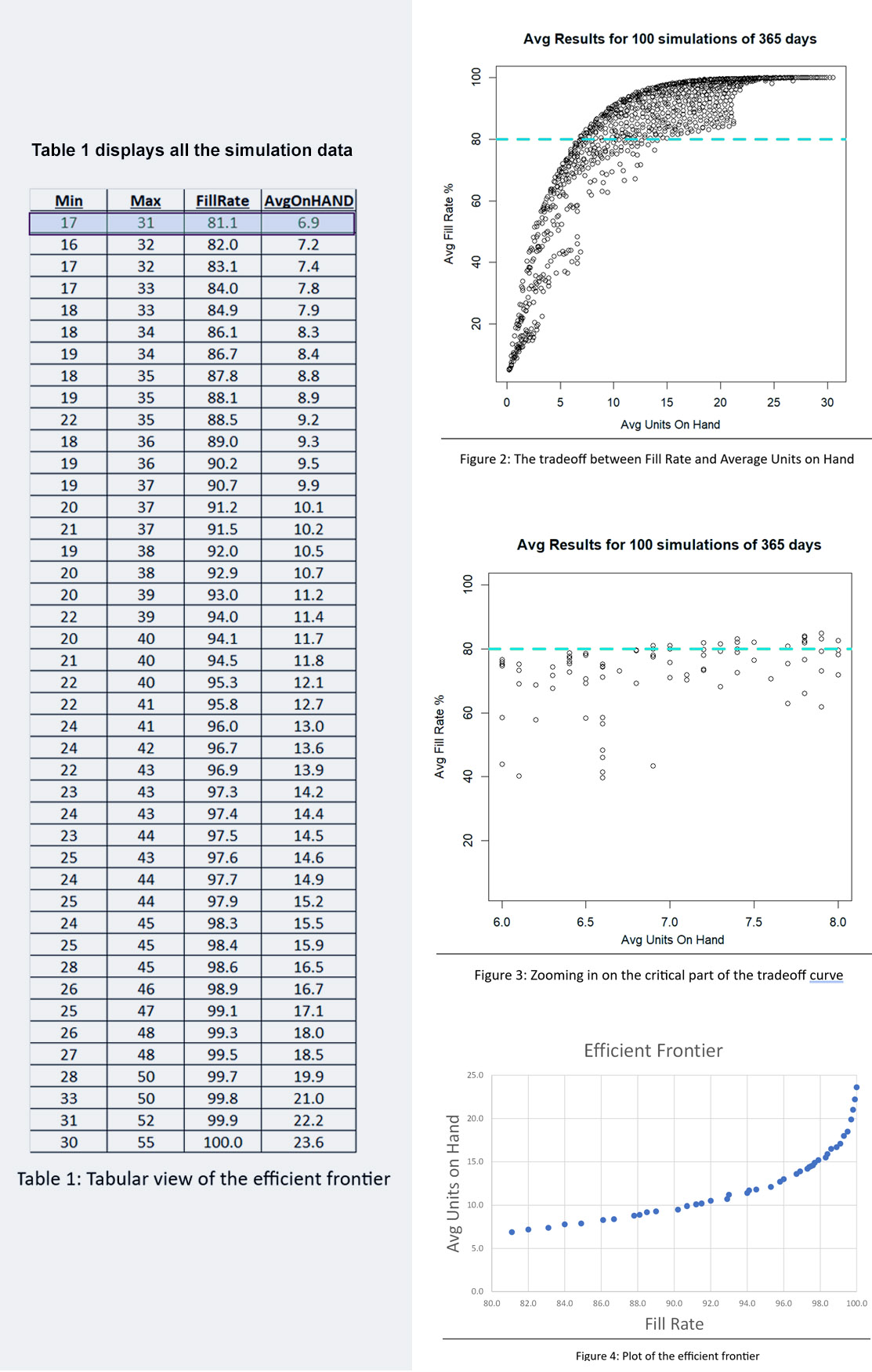
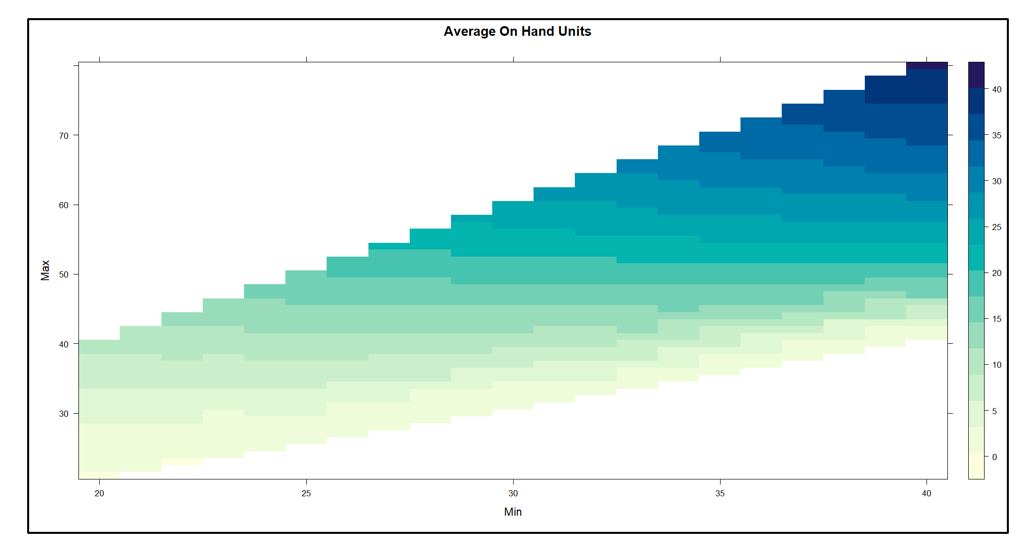
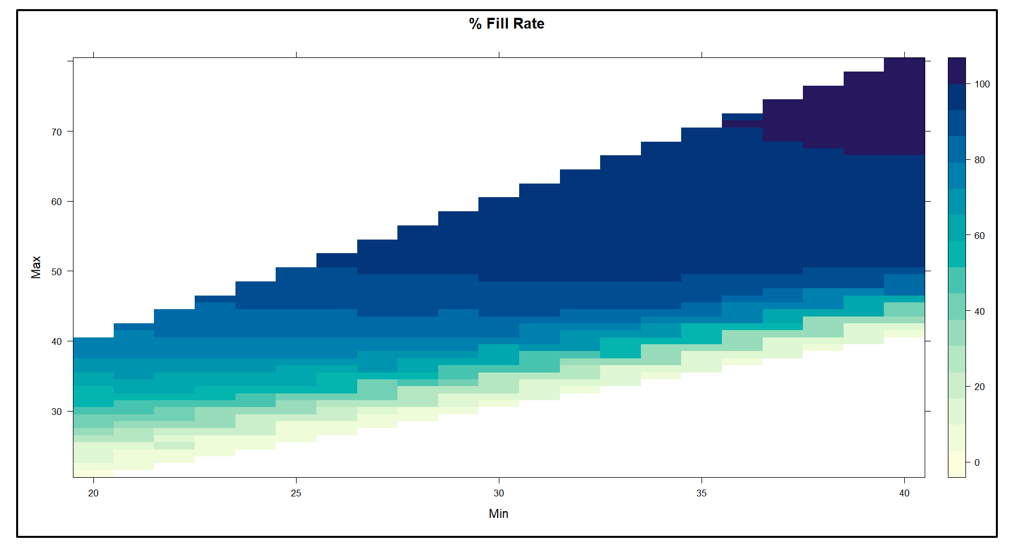
We built a digital twin for this problem and systematically exercised it with 1,085 pairs of Min and Max values. For each pair, we simulated 365 days of operation a total of 100 times. Then we averaged the results to assess the performance of the Min/Max pair in terms of two KPI’s: fill rate and average on hand inventory.

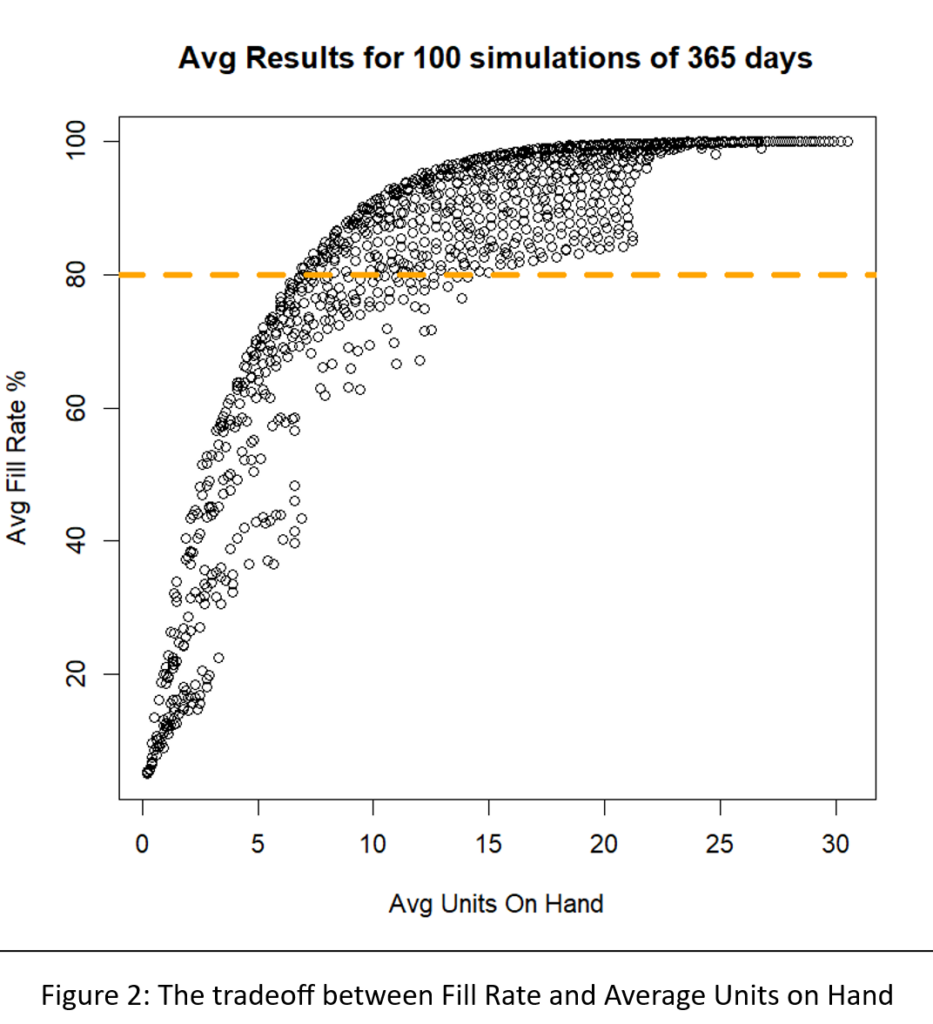
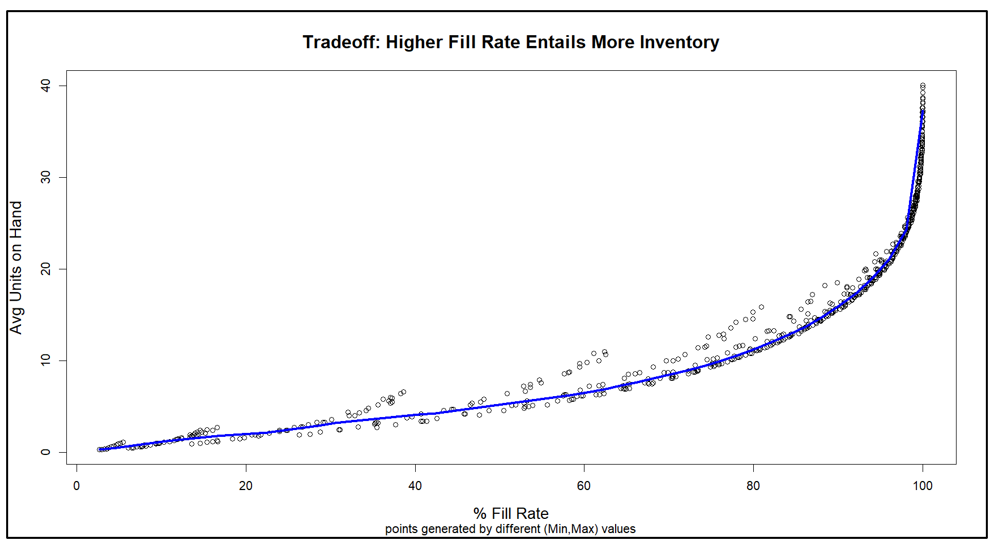
Figure 2 shows the results. The inherent tradeoff between inventory size and fill rate is clear in the figure: if you want a higher fill rate, you have to accept a larger inventory. However, at each level of inventory there is a range of fill rates, so the game is to find the Min/Max pair that yields the highest fill rate for any given size inventory.

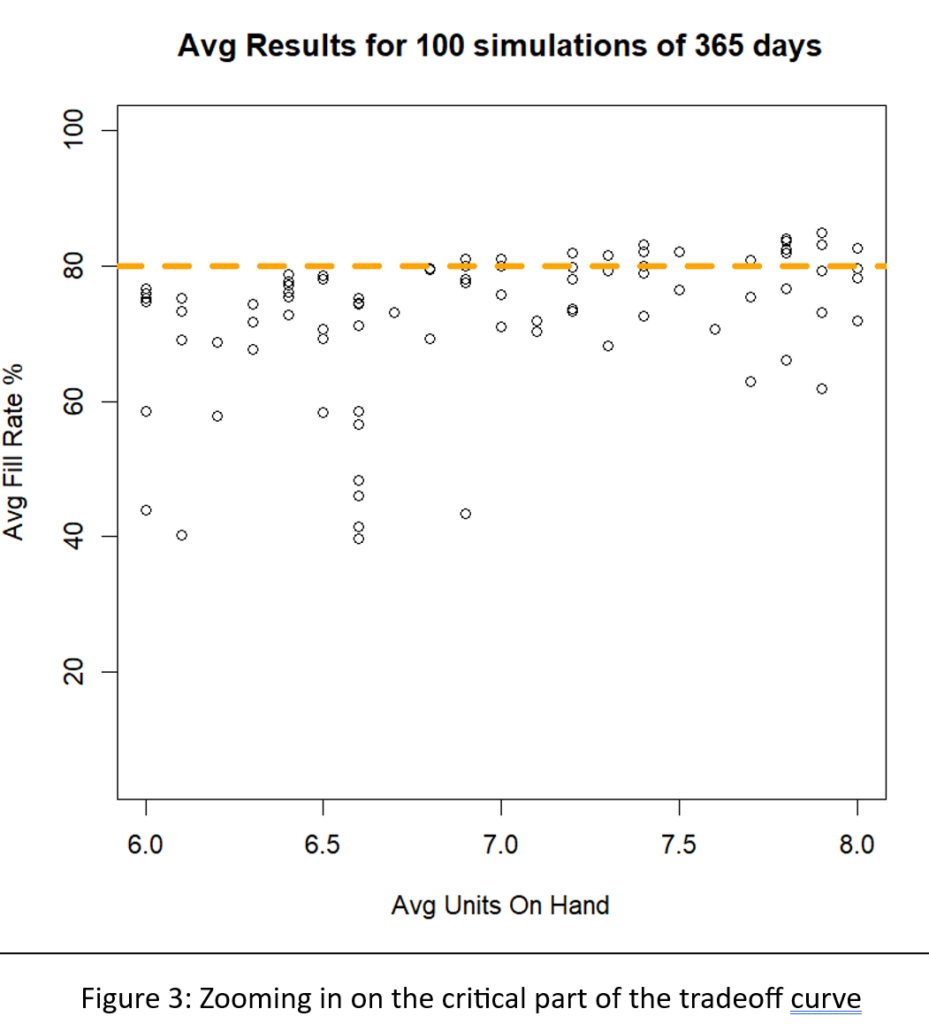
A different way to interpret Figure 2 is to focus on the dashed green line marking the target 80% fill rate. There are many Min/Max pairs that can hit near the 80% target, but they differ in inventory size from about 6 to about 8 units. Figure 3 zooms in on that region of Figure 2 to show  quite a number of Min/Max pairs that are competitive.

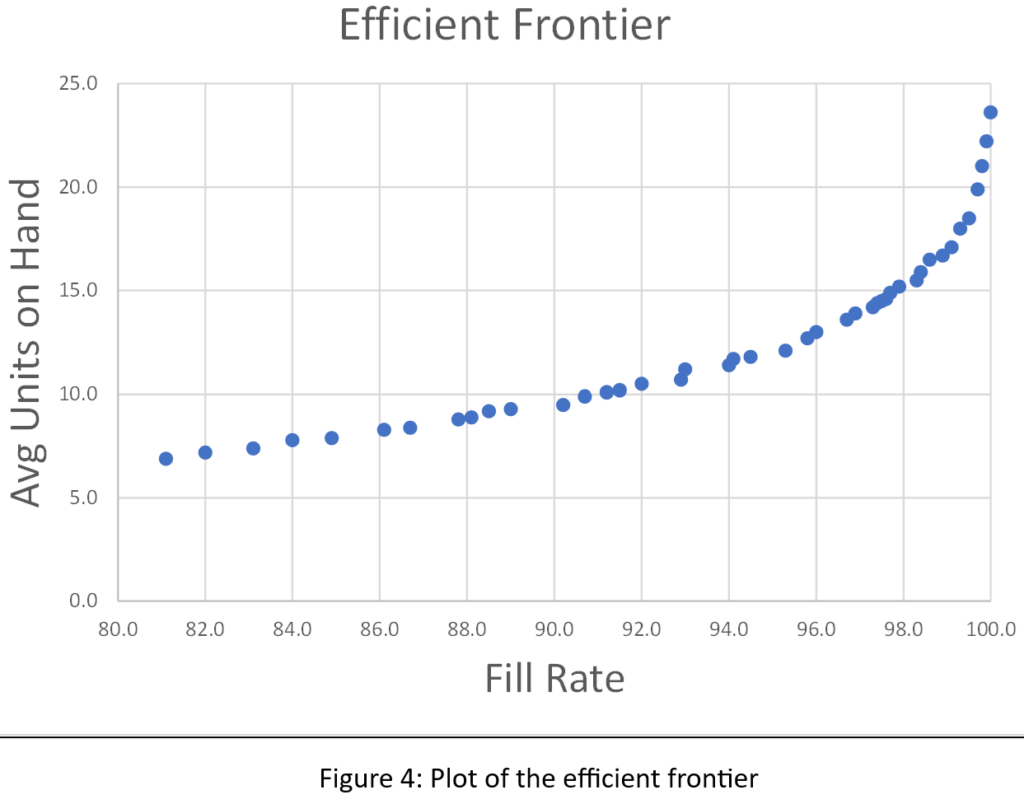
We sorted the results of all 1,085 simulations to identify what economists call the efficient frontier. The efficient frontier is the set of most efficient Min/Max pairs to exploit the tradeoff between fill rate and units on hand. That is, it is a list of Min/Max pairs that provide the least cost way to achieve any desired fill rate, not just 80%. Figure 4 shows the efficient frontier for this problem. Moving from left to right, you can read off the lowest price you would have to pay (as measured by average inventory size) to achieve any target fill rate. For example, to achieve a 90% fill rate, you would have to carry an average inventory of about 10 units.

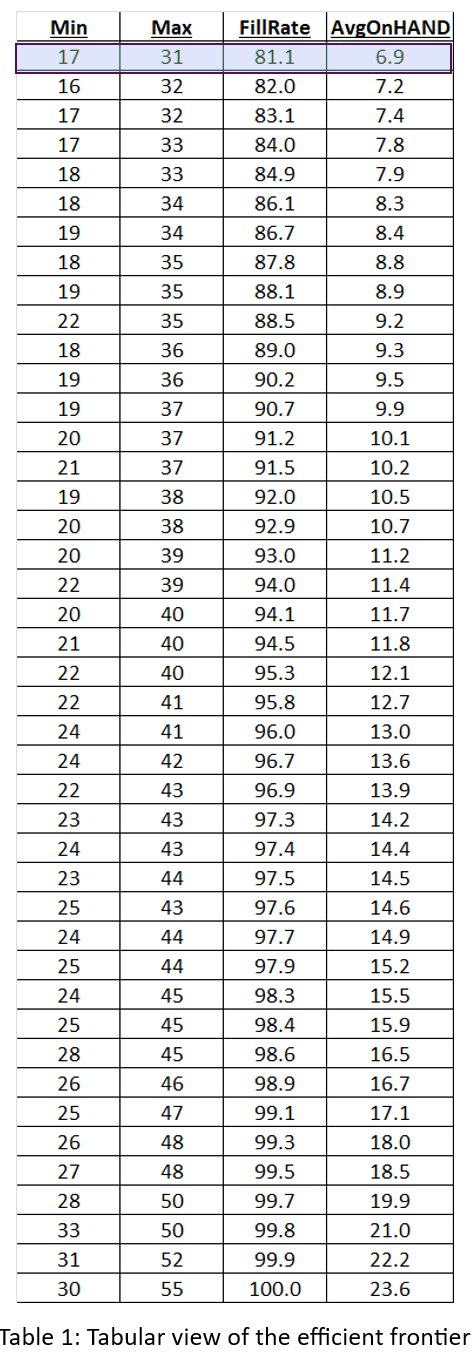
Figures 2, 3, and 4 show results for various Min/Max pairs but do not display the values of Min and Max behind each point. Table 1 displays all the simulation data: the values of Min, Max, average units on hand and fill rate. The answer to the guessing game is highlighted in the first line of the table: Min=7 and Max=13¹. Did you get the right answer, or something close²? Did you maybe get onto the efficient frontier?

Conclusions

Maybe you got lucky, or maybe you do indeed have a Golden Gut, but it’s more likely you didn’t get the right answer, and it’s even more likely you didn’t even try. Figuring out the right answer is extremely difficult without using the digital twin. Guessing is unprofessional.

One step up from guessing is “guess and see”, in which you implement your guess and then wait a while (months?) to see if you like the results. That tactic is at least “scientific”, but it is inefficient.

Now consider the effort to work out the best (Min,Max) pairs for thousands of items. At that scale, there is even less justification for playing the Inventory Guessing Game. The right answer is to play it… Smart³.

¹ This answer has a bonus, in that it achieves a bit more than 80% fill rate at a lower average inventory size than the Min/Max combination that hit exactly 80%. In other words, (7,13) is on the efficient frontier.

² Because these results come from a simulation instead of an exact mathematical equation, there is a certain margin of error associated with each estimated fill rate and inventory level. However, because the average results were based on 100 simulations each 365 days long, the margins of error are small. Across all experiments, the average standard errors in fill rate and mean inventory were, respectively, only 0.009% and 0.129 units.

³ In case you didn’t know this, one of the founders of Smart Software was … Charlie Smart.

Balancing Act

Managing inventory, like managing anything, involves balancing competing priorities. Do you want a lean inventory? Yes! Do you want to be able to say “It’s in stock” when a customer wants to buy something? Yes!

But can you have it both ways? Only to a degree. If you lean into leaning your inventory too aggressively, you risk stockouts. If you stamp out stockouts, you create inventory bloat. You are forced to find a satisfactory balance between the two competing goals of lean inventory and high item availability.

Striking a Balance

How do you strike that balance? Too many inventory planners “guestimate” their way to some kind of answer. Or they work out a smart answer once and hope that it has a distant sell-by date and keep using it while they focus on other problems. Unfortunately, shifts in demand and/or changes in supplier performance and/or shifts in your own company’s priorities will obsolete old inventory plans and put you right back where you started.

It is inevitable that every plan has a shelf life and has to be updated. However, it is definitely not best practice to replace one guess with another. Instead, each planning cycle should exploit modern supply chain software to replace guesswork with fact-based analysis using probability math.

Know Thyself

The one thing that software cannot do is compute a best answer without knowing your priorities. How much do you prioritize lean inventory over item availability? Software will predict the levels of inventory and availability caused by any decisions you make about how to manage each item in your inventory, but only you can decide whether any given set of key performance indicators is consistent with what you want.

Knowing what you want in a general sense is easy: you want it all. But knowing what you prefer when comparing specific scenarios is more difficult. It helps to be able to see a range of realizable possibilities and mull over which seems best when they are laid out side by side.

See What’s Next

Supply chain software can give you a view of the tradeoff curve. You know in general that lean inventory and high item availability trade off against each other, but seeing item-specific tradeoff curves sharpens your focus.

Why is there a curve? Because you have choices about how to manage each item. For instance, if you check inventory status continuously, what values will you assign to the Min and Max values that govern when to order replenishments and how much to order. The tradeoff curve arises because choosing different Min and Max values leads to different levels of on hand inventory and different levels of item availability, e.g., as measured by fill rate.

A Scenario for Analysis

To illustrate these ideas, I used a digital twin  to estimate how various values of Min and Max would perform in a particular scenario. The scenario focused on a notional spare part with purely random demand having a moderately high level of intermittency (37% of days having zero demand). Replenishment lead times were a coin flip between 7 and 14 days. The Min and Max values were systematically varied: Min from 20 to 40 units, Max from Min+1 units to 2xMin units. Each (Min,Max) pair was simulated for 365 days of operation a total of 1,000 times, then the results averaged to estimate both the average number of on hand units and the fill rate, i.e., percentage of daily demands that were satisfied immediately from stock. If stock was not available, it was backordered.

Results

The experiment produced two types of results:

• Plots showing the relationship between Min and Max values and two key performance indicators: Fill rate and average units on hand.
• A tradeoff curve showing how the fill rate and units on hand trade off against each other.

Figure 1 plots on hand inventory as a function of the values of Min and Max. The experiment yielded on hand levels ranging from near 0 to about 40 units.  In general, keeping Min constant and increasing Max results in more units on hand. The relationship with Min is more complex: keeping Max constant,  increasing Min first adds to inventory but at some point reduces it.

Figure 2 plots fill rate as a function of the values of Min and Max.  The experiment yielded fill rate levels ranging from near 0% to 100%.  In general, the functional relationships between the fill rate and the values of Min and Max mirrored those in Figure1.

Figure 3 makes the key point, showing how varying Min and Max produces a perverse pairing of the key performance indicators. Generally speaking, the values of Min and Max that maximize item availability (fill rate)  are the same values that maximize inventory cost (average units on hand). This general pattern is represented by the blue curve. The experiments also produced some offshoots from the blue curve that are associated with poor choices of Min and Max, in the sense that other choices dominate them by producing the same fill rate with lower inventory.

Conclusions

Figure 3 makes clear that your choice of how to manage an inventory item forces you to trade off inventory cost and item availability. You can avoid some inefficient combinations of Min and Max values, but you cannot escape the tradeoff.

The good side of this reality is that you do not have to guess what will happen if you change your current values of Min and Max to something else. The software will tell you what that move will buy you and what it will cost you. You can take off your Guestimator hat and do your thing with confidence.

Figure 1 On Hand Inventory as a function of Min and Max values

Figure 2 Fill Rate as a function of Min and Max values

Figure 3 Tradeoff curve between Fill Rate and On Hand Inventory

Over forty years ago, Smart Software consisted of three friends working to start a company in a church basement. Today, our team has expanded to operate from multiple locations across Massachusetts, New Hampshire and Texas, with team members in England, Spain, Armenia and India. Like many of you in your jobs,  we have found ways to make distributed teams work for us and for you.

This note is about a different kind of teamwork: the collaboration between you and our software that happens at your fingertips. I often write about the software itself and what goes on “under the hood”. This time, my subject is how you should best team up with the software.

Our software suite, Smart Inventory Planning and Optimization (Smart IP&O™) is capable of massively detailed calculations of future demand and the inventory control parameters (e.g., reorder points and order quantities) that would most effectively manage that demand. But your input is required to make the most of all that power. You need to team up with the algorithms.

That interaction can take several forms. You can start by simply assessing how you are doing now. The report writing functions in Smart IP&O (Smart Operational Analytics™) can collate and analyze all your transactional data to measure your Key Performance Indicators (KPIs), both financial (e.g., inventory investment) and operational (e.g., fill rates).

The next step might be to use SIO (Smart Inventory Optimization™), the inventory analytics within SIP&O, to play “what-if” games with the software. For example, you might ask “What if we reduced the order quantity on item 1234 from 50 to 40?” The software grinds the numbers to let you know how that would play out, then you react. This can be useful, but what if you have 50,000 items to consider? You would want to do what-if games for a few critical items, but not all of them.

The real power comes with using the automatic optimization capability in SIO. Here you can team with the algorithms at scale. Using your business judgement, you can create “groups”, i.e., collections of items that share some critical features. For example, you might create a group for “critical spare parts for electric utility customers” consisting of 1,200 parts. Then again calling on your business judgement, you could specify what item availability standard should apply to all the items in that group (e.g., “at least 95% chance of not stocking out in a year”). Now the software can take over and automatically work out the best reorder points and order quantities for every one of those items to achieve your required item availability at the lowest possible total cost. And that, dear reader, is powerful teamwork.

Are you confused about what is AI and what is machine learning? Are you unsure why knowing more will help you with your job in inventory planning? Don’t despair. You’ll be ok, and we’ll show you how some of whatever-it-is can be useful.

What is and what isn’t

What is AI and how does it differ from ML? Well, what does anybody do these days when they want to know something? They Google it. And when they do, the confusion starts.

One source says that the neural net methodology called deep learning is a subset of machine learning, which is a subset of AI. But another source says that deep learning is already a part of AI because it sort of mimics the way the human mind works, while machine learning doesn’t try to do that.

One source says there are two types of machine learning: supervised and unsupervised. Another says there are four: supervised, unsupervised, semi-supervised and reinforcement.

Some say reinforcement learning is machine learning; others call it AI.

Some of us traditionalists call a lot of it “statistics”, though not all of it is.

In the naming of methods, there is a lot of room for both emotion and salesmanship. If a software vendor thinks you want to hear the phrase “AI”, they may well say it for you just to make you happy.

Better to focus on what comes out at the end

You can avoid some confusing hype if you focus on the end result you get from some analytic technology, regardless of its label. There are several analytical tasks that are relevant to inventory planners and demand planners. These include clustering, anomaly detection, regime change detection, and regression analysis. All four methods are usually, but not always, classified as machine learning methods. But their algorithms can come straight out of classical statistics.

Clustering

Clustering means grouping together things that are similar and distancing them from things that are dissimilar. Sometimes clustering is easy: to separate your customers geographically, simply sort them by state or sales region. When the problem is not so dead obvious, you can use data and clustering algorithms to get the job done automatically even when dealing with massive datasets.

For example, Figure 1 illustrates a cluster of “demand profiles”, which in this case divides all a customer’s items into nine clusters based on the shape of their cumulative demand curves. Cluster 1.1 in the top left contains items whose demand has been petering out, while Cluster 3.1 in the bottom left contains items whose demand has accelerated.  Clustering can also be done on suppliers. The choice of number of clusters is typically left to user judgement, but ML can guide that choice.  For example, a user might instruct the software to “break my parts into 4 clusters” but using ML may reveal that there are really 6 distinct clusters the user should analyze. 

Figure 1: Clustering items based on the shapes of their cumulative demand

Anomaly Detection

Demand forecasting is traditionally done using time series extrapolation. For instance, simple exponential smoothing works to find the “middle” of the demand distribution at any time and project that level forward. However, if there has been a sudden, one-time jump up or down in demand in the recent past, that anomalous value can have a significant but unwelcome effect on the near-term forecast.  Just as serious for inventory planning, the anomaly can have an outsized effect on the estimate of demand variability, which goes directly to the calculation of safety stock requirements.

Planners may prefer to find and remove such anomalies (and maybe do offline follow-up to find out the reason for the weirdness). But nobody with a big job to do will want to visually scan thousands of demand plots to spot outliers, expunge them from the demand history, then recalculate everything. Human intelligence could do that, but human patience would soon fail. Anomaly detection algorithms could do the work automatically using relatively straightforward statistical methods. You could call this “artificial intelligence” if you wish.

Regime Change Detection

Regime change detection is like the big brother of anomaly detection. Regime change is a sustained, rather than temporary, shift in one or more aspects of the character of a time series. While anomaly detection usually focuses on sudden shifts in mean demand, regime change could involve shifts in other features of the demand, such as its volatility or its distributional shape.  

Figure 2 illustrates an extreme example of regime change. The bottom dropped out of demand for this item around day 120. Inventory control policies and demand forecasts based on the older data would be wildly off base at the end of the demand history.

Figure 2: An example of extreme regime change in an item with intermittent demand

Here too, statistical algorithms can be developed to solve this problem, and it would be fair play to call them “machine learning” or “artificial intelligence” if so motivated.  Using ML or AI to identify regime changes in demand history enables demand planning software to automatically use only the relevant history when forecasting instead of having to manually pick the amount of history to introduce to the model. 

Regression analysis

Regression analysis relates one variable to another through an equation. For example, sales of window frames in one month may be predicted from building permits issued a few months earlier. Regression analysis has been considered a part of statistics for over a century, but we can say it is “machine learning” since an algorithm works out the precise way to convert knowledge of one variable into a prediction of the value of another.

Summary

It is reasonable to be interested in what’s going on in the areas of machine learning and artificial intelligence. While the attention given to ChatGPT and its competitors is interesting, it is not relevant to the numerical side of demand planning or inventory management. The numerical aspects of ML and AI are potentially relevant, but you should try to see through the cloud of hype surrounding these methods and focus on what they can do.  If you can get the job done with classical statistical methods, you might just do that, then exercise your option to stick the ML label on anything that moves.

Forecasting inventory requirements is a specialized variant of forecasting that focuses on the high end of the range of possible future demand.

For simplicity, consider the problem of forecasting inventory requirements for just one period ahead, say one day ahead. Usually, the forecasting job is to estimate the most likely or average level of product demand. However, if available inventory equals the average demand, there is about a 50% chance that demand will exceed inventory and result in lost sales and/or lost good will. Setting the inventory level at, say, ten times the average demand will probably eliminate the problem of stockouts, but will just as surely result in bloated inventory costs.

The trick of inventory optimization is to find a satisfactory balance between having enough inventory to meet most demand without tying up too many resources in the process. Usually, the solution is a blend of business judgment and statistics. The judgmental part is to define an acceptable inventory service level, such as meeting 95% of demand immediately from stock. The statistical part is to estimate the 95th percentile of demand.

When not dealing with intermittent demand, you can often estimate the required inventory level by assuming a bell-shaped (Normal) curve of demand, estimating both the middle and the width of the bell curve, then using a standard statistical formula to estimate the desired percentile. The difference between the desired inventory level and the average level of demand is called the “safety stock” because it protects against the possibility of stockouts.

When dealing with intermittent demand, the bell-shaped curve is a very poor approximation to the statistical distribution of demand. In this special case, Smart leverages patented technology for intermittent demand that is designed to accurately forecast the ranges and produce a better estimate of the safety stock needed to achieve the required inventory service level.