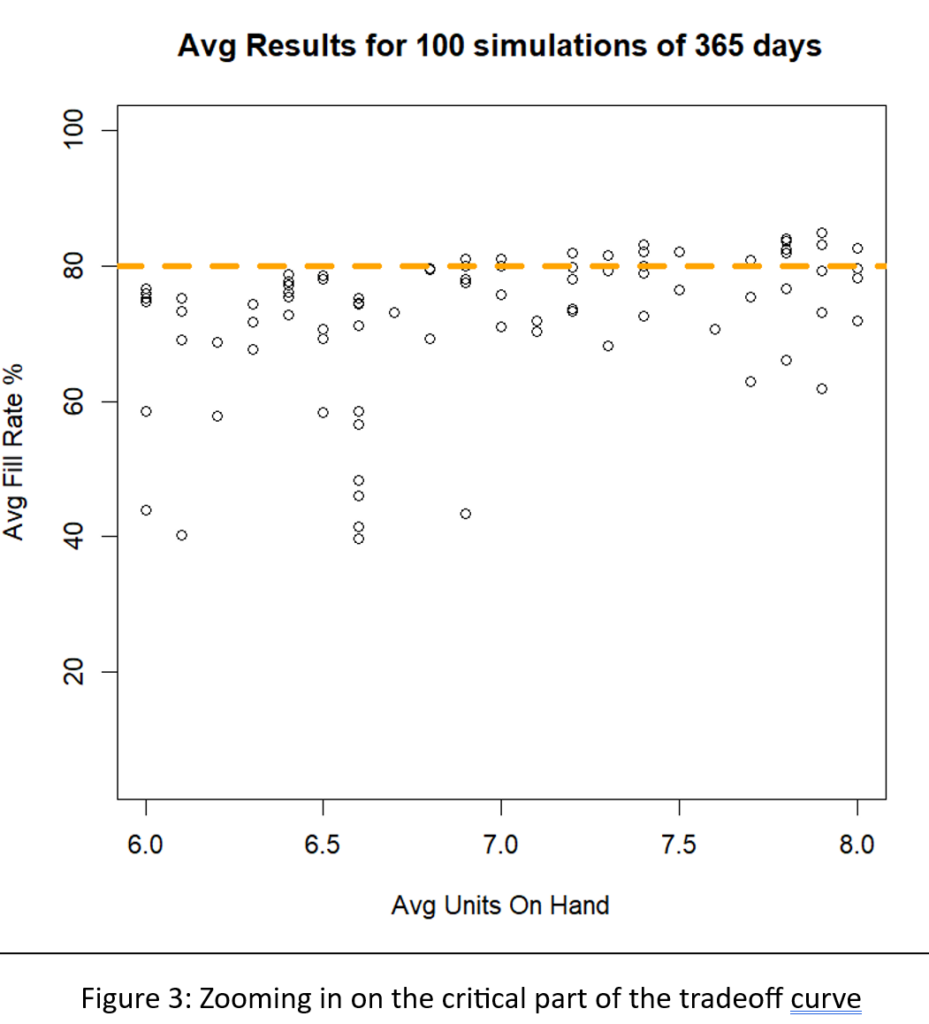
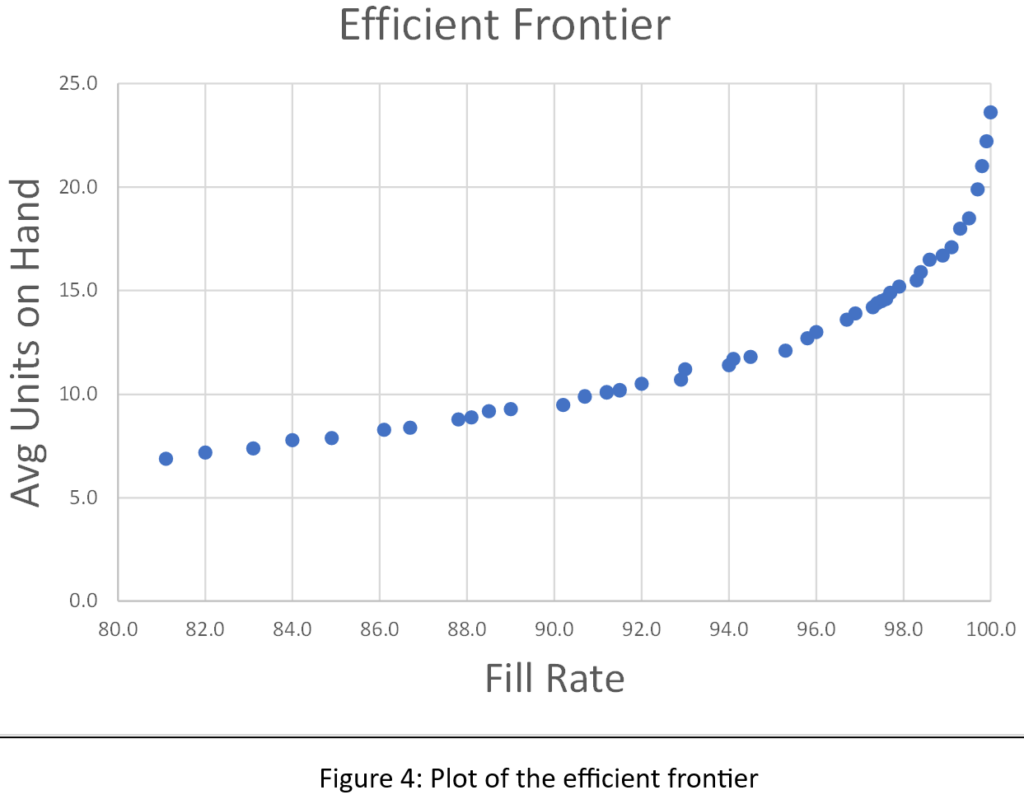
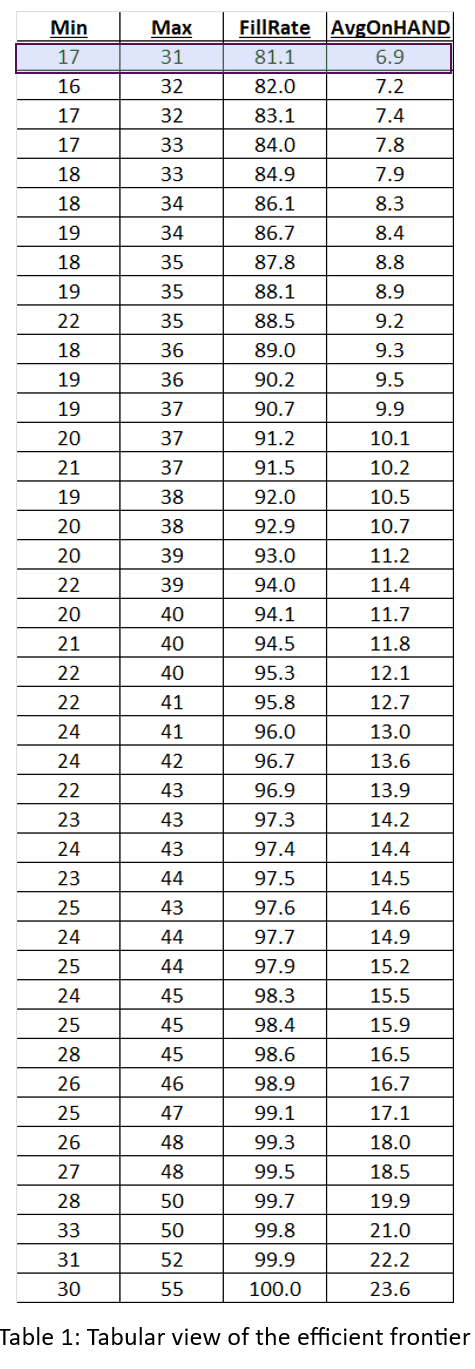
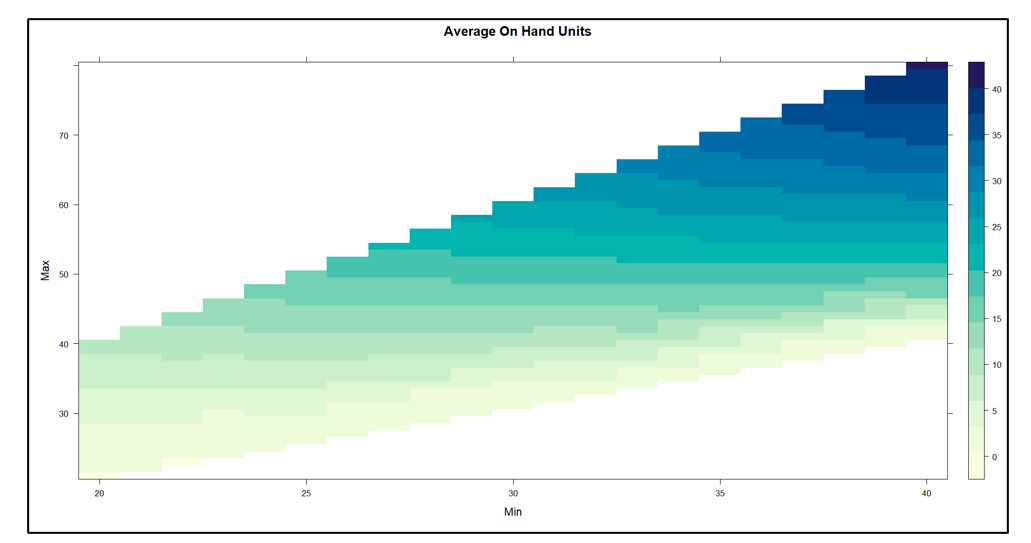
“Business is war” may be an overdone metaphor but it’s not without validity. Like the “Bomber Gap” and the “Missile Gap,” worries about falling behind the competition, and the resulting threat of annihilation, always lurk in the minds of business executives, If they don’t, they should, because not all gaps are imaginary (the Bomber Gap and the Missile Gap were shown to not exist between the US and the USSR, but the 1980’s gap between Japanese and American productivity was all too real). The difference between paranoia and justified concern is converting fear into facts. This post is about organizing your attention toward possible gaps in your company’s supply chain analytics.

Surveillance Gaps

The US Army has a saying: “Time spent on reconnaissance is never wasted.” Now and then, our Smart Forecaster blog has a post that helps you get your head on a swivel to see what’s going on around you. An example is our post on digital twins, which is a hot topic throughout the engineering world.  To recap: using demand and supply simulations to probe for weaknesses in your inventory plan is a form of supply chain reconnaissance.  Closing this surveillance gap enables businesses to take corrective action before an actual problem emerges.

Situational Awareness Gaps

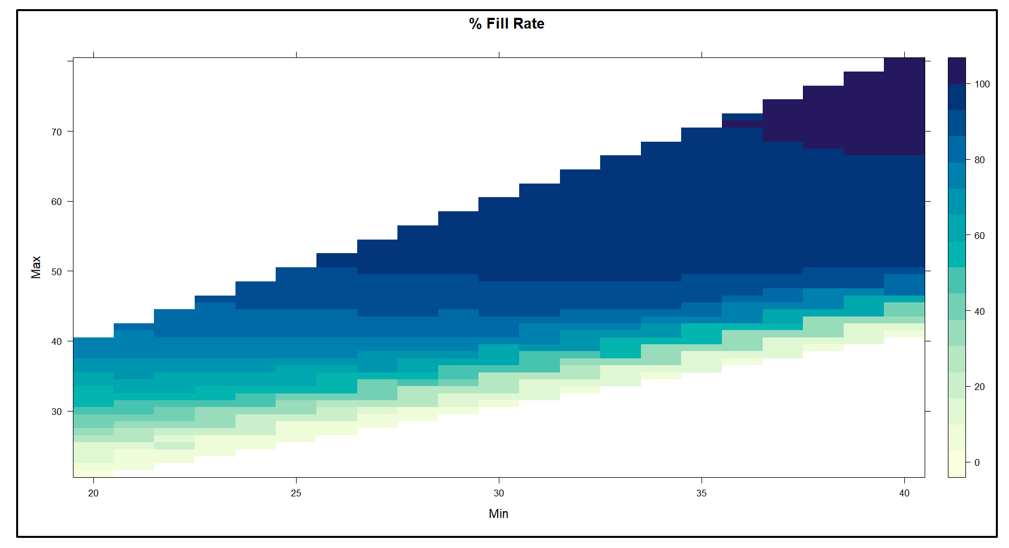
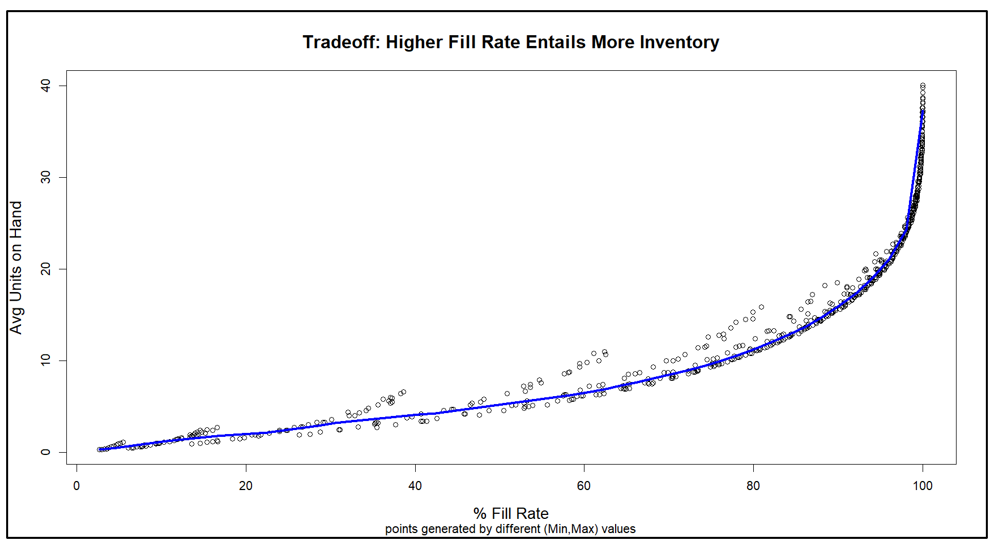
A military commander needs to keep track of what is available for use and how well it is being used. The reports available in Smart Operational Analytics keep you current on your inventory counts, your forecasting accuracy, your suppliers’ responsiveness, and trends in these and other operational areas.  You’ll know exactly where you stand on a variety of supply chain KPIs such as service level, fill rates, and inventory turns.  You’ll know whether actual performance is aligned with planned performance and whether the inventory plan (i.e., what to order, when, from whom, and why) is being adhered to or ignored.

Agility Gaps

The business environment can change rapidly. All it takes is a tanker stuck sideways in the Suez Canal, a few anti-ship ballistic missiles in the Red Sea, or a region-wide weather event. These catastrophes may fall as much on your competitors’ heads as on yours, but which of you is agile enough to react first? Exception reporting in Demand Planner and Smart Operational Analytics can detect major changes in the character of demand so you can quickly filter out obsolete demand data before they poison all your calculations for demand forecasts or inventory optimization. Smart Demand Planner can give advance warning of a pending increase or decrease in demand. Smart Inventory Optimization can help you adjust your inventory replenishment tactics to reflect these shifts in demand.

Innovation Gaps

Whether you refer to your competition as “The Other Guys” or “Everybody Else” or something unprintable, the ones you have to worry about are the ones always looking for an edge. When you choose Smart as your partner, we’ll give you that edge with innovative but field proven predictive solutions.  Smart Software has been innovating predictive modeling since birth over 40 years ago.

• Our first products introduced multiple technical innovations: assessment of forecast quality by looking into the future not the past; automatic selection of the best among a set of competing methodologies, exploiting the graphics in the first PCs to allow easy management overrides of statistical forecasts.

• Later we invented and patented a radically different approach to forecasting the intermittent demand that is characteristic of both spare parts and big-ticket durable goods. Our technology was patented, received multiple awards for dramatically improving the management of inventory.  The solution is now a field proven approach used by many leading businesses in service parts, MRO, aftermarket parts, and field service.

• More recently, Smart’s cloud platform for demand forecasting, predictive modeling, inventory optimization, and analytics, takes all relevant data otherwise locked in your ERP or EAM systems, external files, and other disparate data sources, organizes it in the Smart Data Pipeline, structures it into our common data model, and processes it in our AWS cloud.  Smart uses the power of our patented probabilistic demand simulations in Smart Inventory Optimization to stress test and optimize the rules you use to manage each of your inventory items.

It’s my job, along with my cofounder Dr. Nelson Hartunian, our data science team, and academic consultants, to continue to push the envelope of supply chain analytics and bring the benefits back to you by continuously rolling out new versions of our products so you don’t get stuck in an innovation gap – or any of the others.

Our customers have usually settled into one way to manage their service parts inventory. The professor in me would like to think that the chosen inventory policy was a reasoned choice among considered alternatives, but more likely it just sort of happened. Maybe the inventory honcho from long ago had a favorite and that choice stuck. Maybe somebody used an EAM or ERP system that offered only one choice. Perhaps there were some guesses made, based on the conditions at the time.

The Competitors

Too seldom, businesses make these choices in haphazard ways. But modern service parts planning software lets you be more systematic about your choices. This post demonstrates that proposition by making objective comparisons among three popular inventory policies:  Order Up To, Reorder Point/Order Quantity, and Min/Max.  I discussed each of these policies in this video blog.

• Order Up To. This is a periodic review policy where every T days, on-hand inventory is tallied and an order of random size is placed to bring the stock level back up to S units.
• Q, R or Reorder Point/Order Quantity. Q, R is a continuous review policy where every day, inventory is tallied. If there are Q or fewer units on hand, an order of fixed size is placed for R more units.
• Min, Max is another continuous review policy where every day, inventory is tallied. If there are Min or fewer units on hand, an order is placed to bring the stock level back up to Max units.

Inventory theory says these choices are listed in increasing order of effectiveness. The first option, Order Up To, is clearly the simplest and cheapest to implement, but it closes its eyes to what’s going on for long periods of time.  Imposing a specified passage of time in between orders makes it, in theory, less flexible. In contrast, the two continuous review options keep an eye on what’s happening all the time, so they can react to potential stockouts quicker. The Min/Max option is, in theory, more flexible than the option that uses a fixed reorder quantity because the size of the order dynamically changes to accommodate the demand.

That’s the theory. This post examines evidence from head-to-head comparisons to check the theory and put concrete numbers on the relative performance of the three policies.

The Meaning of “Best”

How should we keep score in this tournament? If you are a regular reader of this Smart Forecaster blog, you know that the core of inventory planning is a tug-of-war between two opposing objectives: keeping inventory lean vs keeping item availability metrics such as service level high.

To simplify things, we will compute “one number to rule them all”: the average operating cost. The winning policy will be the one with the lowest average.

This average is the sum of three components: the cost of holding inventory (“holding cost”), the cost of ordering replenishment units (“ordering cost”) and the cost of losing a sale (“shortage cost”). To make things concrete, we used the following assumptions:

• Each service part is valued at $1,000.
• Annual holding cost is 10% of item value, or $100 per year per unit.
• Processing each replenishment order costs $20 per order.
• Each unit demanded but not provided costs the value of the part, $1,000.

For simplicity, we will refer to the average operating cost as simply “the cost”.

Of course, the lowest average cost can be achieved by getting out of the business. So the competition required a performance constraint on item availability: Each option had to achieve a fill rate of at least 99%.

The Alternatives Duke it Out

A key element of context is whether stockouts result in losses or backorders. Assuming that the service part in question is critical, we assumed that unfilled orders are lost, which means that a competitor fills the order. In an MRO environment, this will mean additional downtime due to stockout.

To compare the alternatives, we used our predictive modeling engine to run a large number of Monte Carlo simulations.  Each simulation involved specifying the parameter values of each policy (e.g., Min and Max values), generating a demand scenario, feeding that into the logic of the policy, and measuring the resulting cost averaged over 365 days of operation. Repeating this process 1,000 times and averaging the 1,000 resulting costs gave the final result for each policy.  

To make the comparison fair, each alternative had to be designed for its best performance. So we searched the “design space” of each policy to find the design with the lowest cost. This required repeating the process described in the previous paragraph for many pairs of parameter values and identifying the pair yielding the lost average annual operating cost.

Using the algorithms in Smart Inventory Optimization (SIO^TM) we made head-to-head-to-head comparisons under the following assumptions about demand and supply:

• Item demand was assumed to be intermittent and highly variable but relatively simple in that there was neither trend nor seasonality, as is often true for service parts. Daily mean demand was 5 units with a large standard deviation of 13 units. Figure 1 shows a sample of one year’s demand. We have chosen a very challenging demand pattern, in which some days have 10 to even 20 times the average demand.

Figure 1: Daily part demand was assumed to be intermittent and very spikey.

​​

• Suppliers’ replenishment lead times were 14 days 75% of the time and 21 days otherwise. This reflects the fact that there is always uncertainty in the supply chain.

And the Winner Is…

Was the theory right? Kinda’ sorta’.

Table 1 shows the results of the simulation experiments. For each of the three competing policies, it shows the average annual operating cost, the margin of error (technically, an approximate 95% confidence interval for the mean cost), and the apparent best choices for parameter values.

Table 1: Results of the simulated comparisons

For example, the average cost for the (T,S) policy when T is fixed at 30 days was $41,680. But the Plus/Minus implies that the results are compatible with a “true” cost (i.e., the estimate from an infinite number of simulations) of anywhere between $39,890 and $43,650. The reason there is so much statistical uncertainty is the extremely spikey nature of demand in this example.

Table 1 says that, in this example, the three policies fall in line with expectations. However, more useful conclusions would be:

1. The three policies are remarkably similar in average cost. By clever choice of parameter values, one can get good results out of any of the three policies.
2. Not shown in Table 1, but clear from the detailed simulation results, is that poor choices for parameter values can be disastrous for any policy.
3. It is worth noting that the periodic review (T,S) policy was not allowed to optimize over possible values of T. We fixed T at 30 to mimic what is common in practice, but those who use the periodic review policy should consider other review periods. An additional experiment fixed the review period at T = 7 days. The average cost in this scenario was minimized at $36,551 ± $1,668 with S = 343. This result is better than that using T = 30 days.
4. We should be careful about over-generalizing these results. They depend on the assumed values of the three cost parameters (holding, ordering and shortage) and the character of the demand process.
5. It is possible to run experiments like those shown here automatically in Smart Inventory Optimization. This means that you too would be able to explore design choices in a rigorous way.

Those of you who track hot topics will be familiar with the term “digital twin.” Those who have been too busy with work may want to read on and catch up.

What is a digital twin?

While there are several definitions of digital twin, here’s one that works well:

A digital twin is a dynamic virtual copy of a physical asset, process, system, or environment that looks like and behaves identically to its real-world counterpart. A digital twin ingests data and replicates processes so you can predict possible performance outcomes and issues that the real-world product might undergo. [Source: Unity.com]. For additional background, you might go to Mckinsey.com.

What is the difference between a digital twin (hereafter DT) and a model? Primarily, a DT gets connected to real-time data to maintain the model as an up-to-the-minute representation of the system you are working with.

Our current products might be called “slow-motion DT’s” because they are usually used with non-real-time data (though not stale data, since it is updated overnight) and applied to problems like planning the next quarter’s raw material buys or setting inventory parameters for a month or longer.

Are people using digital twins in my industry?

My impression is that the penetration of DT’s may be highest in the aerospace and nuclear industries. Most of our customers are elsewhere: in manufacturing, distribution, and public utilities such as transportation and power. Soon we’ll be offering new products that come closer to the strict definition of a DT that is connected intimately to the system it represents.

DT Preview

Most users of Smart Inventory Optimization™ (SIO) run the application periodically, typically monthly. SIO analyzes current demand for inventory items and recent supplier lead times, converting these into demand and supply scenarios, respectively. Then users either interactively (for individual items) or automatically (at scale) set inventory control parameters that will provide the long-term average performance they want, balancing the competing goals of minimizing inventory while guaranteeing a sufficient level of item availability.

Smart Supply Planner (SSP) operates in a more immediate way to react to contingencies. Any day could bring an anomalous order that spikes up demand, such as when a new customer places a surprising initial stocking order. Or a key supplier could experience a problem at its factory and be forced to delay shipment of your planned replenishment orders. In the long run, these contingencies average out and justify the recommendations coming out of SIO. However, SSP will give you a way to react in the short run to seize opportunities or dodge bullets.

At its core, SSP operates like SIO in that it is scenario driven. The differences are that it uses short planning horizons and uses real-time initial conditions as the basis for its simulations of inventory system performance. Then it will provide real-time recommendations for interventions that offset the disruption caused by the contingencies. These would include cancelling or expediting replenishment orders.

Summary

Digital twins let you try out plans “in silico” before you implement them in the factory or warehouse. At their core are mathematical models of your operation but connected to real-time data. They provide a “digital sandbox” in which you can try out ideas and get immediate predictions of how well they will work. Much more than a spreadsheet, DT’s will soon be the key tool in your inventory planning toolbox.

Some companies invest in software to help them manage their inventory, whether it’s spare parts or finished goods. But a surprising number of others play the Inventory Guessing Game every day, trusting to an imagined “Golden Gut” or to plain luck to set their inventory control parameters. But what kind of results do you expect with that approach?

How good are you at intuiting the right values? This blog post challenges you to guess the best Min and Max values for a notional inventory item. We’ll show you its demand history, give you a few relevant facts, then you can pick Min and Max values and see how well they would work. Ready?

The Challenge

Figure 1 shows the daily demand history of the item. The average demand is 2 units per day. Replenishment lead time is a constant 10 days (which is unrealistic but works in your favor). Orders that cannot be filled immediately from stock cannot be backordered and are lost. You want to achieve at least an 80% fill rate, but not at any cost. You also want to minimize the average number of units on hand while still achieving at least an 80% fill rate. What Min and Max values would produce an 80% fill rate with the lowest average number of units on hand? [Record your answers for checking later. The solution appears below at the end of the article.]

Computing the Best Min and Max Values

The way to determine the best values is to use a digital twin, also known as a Monte Carlo simulation. The analysis creates a multitude of demand scenarios and passes them through the mathematical logic of the inventory control system to see what values will be taken on by key performance indicators (KPI’s).

We built a digital twin for this problem and systematically exercised it with 1,085 pairs of Min and Max values. For each pair, we simulated 365 days of operation a total of 100 times. Then we averaged the results to assess the performance of the Min/Max pair in terms of two KPI’s: fill rate and average on hand inventory.

Figure 2 shows the results. The inherent tradeoff between inventory size and fill rate is clear in the figure: if you want a higher fill rate, you have to accept a larger inventory. However, at each level of inventory there is a range of fill rates, so the game is to find the Min/Max pair that yields the highest fill rate for any given size inventory.

A different way to interpret Figure 2 is to focus on the dashed green line marking the target 80% fill rate. There are many Min/Max pairs that can hit near the 80% target, but they differ in inventory size from about 6 to about 8 units. Figure 3 zooms in on that region of Figure 2 to show  quite a number of Min/Max pairs that are competitive.

We sorted the results of all 1,085 simulations to identify what economists call the efficient frontier. The efficient frontier is the set of most efficient Min/Max pairs to exploit the tradeoff between fill rate and units on hand. That is, it is a list of Min/Max pairs that provide the least cost way to achieve any desired fill rate, not just 80%. Figure 4 shows the efficient frontier for this problem. Moving from left to right, you can read off the lowest price you would have to pay (as measured by average inventory size) to achieve any target fill rate. For example, to achieve a 90% fill rate, you would have to carry an average inventory of about 10 units.

Figures 2, 3, and 4 show results for various Min/Max pairs but do not display the values of Min and Max behind each point. Table 1 displays all the simulation data: the values of Min, Max, average units on hand and fill rate. The answer to the guessing game is highlighted in the first line of the table: Min=7 and Max=13¹. Did you get the right answer, or something close²? Did you maybe get onto the efficient frontier?

Conclusions

Maybe you got lucky, or maybe you do indeed have a Golden Gut, but it’s more likely you didn’t get the right answer, and it’s even more likely you didn’t even try. Figuring out the right answer is extremely difficult without using the digital twin. Guessing is unprofessional.

One step up from guessing is “guess and see”, in which you implement your guess and then wait a while (months?) to see if you like the results. That tactic is at least “scientific”, but it is inefficient.

Now consider the effort to work out the best (Min,Max) pairs for thousands of items. At that scale, there is even less justification for playing the Inventory Guessing Game. The right answer is to play it… Smart³.

¹ This answer has a bonus, in that it achieves a bit more than 80% fill rate at a lower average inventory size than the Min/Max combination that hit exactly 80%. In other words, (7,13) is on the efficient frontier.

² Because these results come from a simulation instead of an exact mathematical equation, there is a certain margin of error associated with each estimated fill rate and inventory level. However, because the average results were based on 100 simulations each 365 days long, the margins of error are small. Across all experiments, the average standard errors in fill rate and mean inventory were, respectively, only 0.009% and 0.129 units.

³ In case you didn’t know this, one of the founders of Smart Software was … Charlie Smart.

Balancing Act

Managing inventory, like managing anything, involves balancing competing priorities. Do you want a lean inventory? Yes! Do you want to be able to say “It’s in stock” when a customer wants to buy something? Yes!

But can you have it both ways? Only to a degree. If you lean into leaning your inventory too aggressively, you risk stockouts. If you stamp out stockouts, you create inventory bloat. You are forced to find a satisfactory balance between the two competing goals of lean inventory and high item availability.

Striking a Balance

How do you strike that balance? Too many inventory planners “guestimate” their way to some kind of answer. Or they work out a smart answer once and hope that it has a distant sell-by date and keep using it while they focus on other problems. Unfortunately, shifts in demand and/or changes in supplier performance and/or shifts in your own company’s priorities will obsolete old inventory plans and put you right back where you started.

It is inevitable that every plan has a shelf life and has to be updated. However, it is definitely not best practice to replace one guess with another. Instead, each planning cycle should exploit modern supply chain software to replace guesswork with fact-based analysis using probability math.

Know Thyself

The one thing that software cannot do is compute a best answer without knowing your priorities. How much do you prioritize lean inventory over item availability? Software will predict the levels of inventory and availability caused by any decisions you make about how to manage each item in your inventory, but only you can decide whether any given set of key performance indicators is consistent with what you want.

Knowing what you want in a general sense is easy: you want it all. But knowing what you prefer when comparing specific scenarios is more difficult. It helps to be able to see a range of realizable possibilities and mull over which seems best when they are laid out side by side.

See What’s Next

Supply chain software can give you a view of the tradeoff curve. You know in general that lean inventory and high item availability trade off against each other, but seeing item-specific tradeoff curves sharpens your focus.

Why is there a curve? Because you have choices about how to manage each item. For instance, if you check inventory status continuously, what values will you assign to the Min and Max values that govern when to order replenishments and how much to order. The tradeoff curve arises because choosing different Min and Max values leads to different levels of on hand inventory and different levels of item availability, e.g., as measured by fill rate.

A Scenario for Analysis

To illustrate these ideas, I used a digital twin  to estimate how various values of Min and Max would perform in a particular scenario. The scenario focused on a notional spare part with purely random demand having a moderately high level of intermittency (37% of days having zero demand). Replenishment lead times were a coin flip between 7 and 14 days. The Min and Max values were systematically varied: Min from 20 to 40 units, Max from Min+1 units to 2xMin units. Each (Min,Max) pair was simulated for 365 days of operation a total of 1,000 times, then the results averaged to estimate both the average number of on hand units and the fill rate, i.e., percentage of daily demands that were satisfied immediately from stock. If stock was not available, it was backordered.

Results

The experiment produced two types of results:

• Plots showing the relationship between Min and Max values and two key performance indicators: Fill rate and average units on hand.
• A tradeoff curve showing how the fill rate and units on hand trade off against each other.

Figure 1 plots on hand inventory as a function of the values of Min and Max. The experiment yielded on hand levels ranging from near 0 to about 40 units.  In general, keeping Min constant and increasing Max results in more units on hand. The relationship with Min is more complex: keeping Max constant,  increasing Min first adds to inventory but at some point reduces it.

Figure 2 plots fill rate as a function of the values of Min and Max.  The experiment yielded fill rate levels ranging from near 0% to 100%.  In general, the functional relationships between the fill rate and the values of Min and Max mirrored those in Figure1.

Figure 3 makes the key point, showing how varying Min and Max produces a perverse pairing of the key performance indicators. Generally speaking, the values of Min and Max that maximize item availability (fill rate)  are the same values that maximize inventory cost (average units on hand). This general pattern is represented by the blue curve. The experiments also produced some offshoots from the blue curve that are associated with poor choices of Min and Max, in the sense that other choices dominate them by producing the same fill rate with lower inventory.

Conclusions

Figure 3 makes clear that your choice of how to manage an inventory item forces you to trade off inventory cost and item availability. You can avoid some inefficient combinations of Min and Max values, but you cannot escape the tradeoff.

The good side of this reality is that you do not have to guess what will happen if you change your current values of Min and Max to something else. The software will tell you what that move will buy you and what it will cost you. You can take off your Guestimator hat and do your thing with confidence.

Figure 1 On Hand Inventory as a function of Min and Max values

Figure 2 Fill Rate as a function of Min and Max values

Figure 3 Tradeoff curve between Fill Rate and On Hand Inventory