Forecasting inventory requirements is a specialized variant of forecasting that focuses on the high end of the range of possible future demand.

For simplicity, consider the problem of forecasting inventory requirements for just one period ahead, say one day ahead. Usually, the forecasting job is to estimate the most likely or average level of product demand. However, if available inventory equals the average demand, there is about a 50% chance that demand will exceed inventory and result in lost sales and/or lost good will. Setting the inventory level at, say, ten times the average demand will probably eliminate the problem of stockouts, but will just as surely result in bloated inventory costs.

The trick of inventory optimization is to find a satisfactory balance between having enough inventory to meet most demand without tying up too many resources in the process. Usually, the solution is a blend of business judgment and statistics. The judgmental part is to define an acceptable inventory service level, such as meeting 95% of demand immediately from stock. The statistical part is to estimate the 95th percentile of demand.

When not dealing with intermittent demand, you can often estimate the required inventory level by assuming a bell-shaped (Normal) curve of demand, estimating both the middle and the width of the bell curve, then using a standard statistical formula to estimate the desired percentile. The difference between the desired inventory level and the average level of demand is called the “safety stock” because it protects against the possibility of stockouts.

When dealing with intermittent demand, the bell-shaped curve is a very poor approximation to the statistical distribution of demand. In this special case, Smart leverages patented technology for intermittent demand that is designed to accurately forecast the ranges and produce a better estimate of the safety stock needed to achieve the required inventory service level.

Summary

Smart Software’s advanced supply chain analytics exploits multiple advanced methods. Two of the most important are “statistical bootstrapping” and “Monte Carlo simulation”. Since both involve lots of random numbers flying around, folks sometimes get confused about which is which and what they are good for. Hence, this note. Bottom line up front: Statistical bootstrapping generates demand scenarios for forecasting. Monte Carlo simulation uses the scenarios for inventory optimization.

Bootstrapping

Bootstrapping, also called “resampling” is a method of computational statistics that we use to create demand scenarios for forecasting. The essence of the forecasting problem is to expose possible futures that your company might confront so you can work out how to manage business risks. Traditional forecasting methods focus on computing “most likely” futures, but they fall short of presenting the full risk picture. Bootstrapping provides an unlimited number of realistic what-if scenarios.

Bootstrapping does this without making unrealistic assumptions about the demand, i.e., that it is not intermittent, or that it has a bell-shaped distribution of sizes. Those assumptions are crutches to make the math simpler, but the bootstrap is a procedure,  not an equation, so it doesn’t need such simplifications.

For the simplest demand type, which is a stable randomness with no seasonality or trend, bootstrapping is dead easy. To get a reasonable idea of what a single future demand value might be, pick one of the historical demands at random. To create a demand scenario, make multiple random selections from the past and string them together. Done. It is possible to add a little more realism by “jittering” the demand values, i.e., adding or subtracting a bit of additional randomness to each one, but even that is simple.

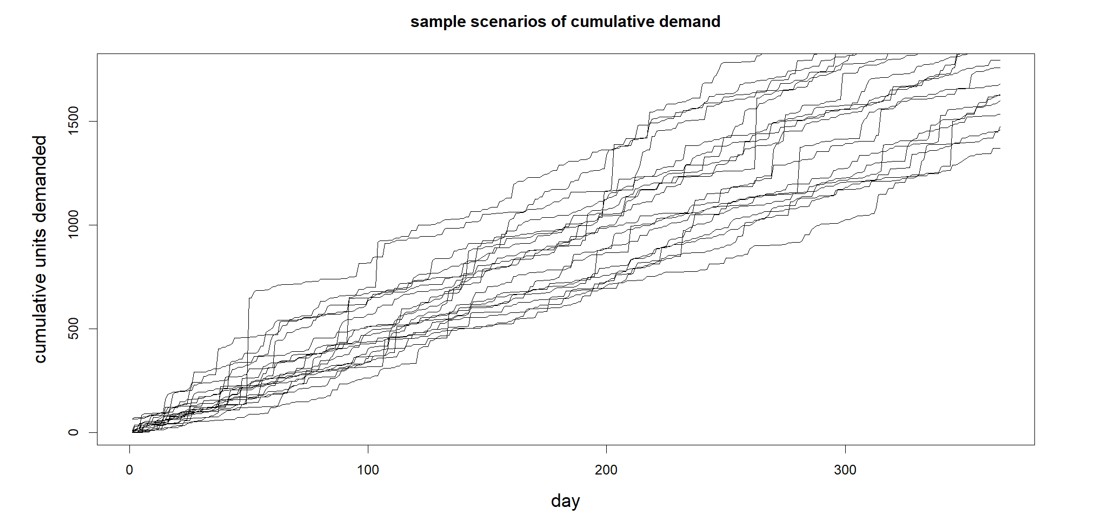
Figure 1 shows a simple bootstrap. The first line is a short sequence of historical demand for an SKU. The following lines show scenarios of future demand created by randomly selecting values from the demand history. For instance, the next three demand might be (0, 14, 6), or (2, 3, 5), etc.

Figure 1: Example of demand scenarios generated by a simple bootstrap

Higher frequency operations such as daily forecasting bring with them more complex demand patterns, such as double seasonality (e.g., day-of-week and month-of-year) and/or trend. This challenged us to invent a new generation of bootstrapping algorithms. We recently won a US Patent for this breakthrough, but the essence is as described above.

Monte Carlo Simulation

Monte Carlo is famous for its casinos, which, like bootstrapping, invoke the idea of randomness. Monte Carlo methods go back a long way, but the modern impetus came with the need to do some hairy calculations about where neutrons would fly when an A-bomb explodes.

The essence of Monte Carlo analysis is this: “Our problem is too complicated to analyze with paper-and-pencil equations. So, let’s write a computer program that codes the individual steps of the process, put in the random elements (e.g., which way a neutron shoots away), wind it up and watch it go. Since there’s a lot of randomness, let’s run the program a zillion times and average the results.”

Applying this approach to inventory management, we have a different set of randomly occurring events: e.g., a demand of a given size arrives on a random day, a replenishment of a given size arrives after a random lead time, we cut a replenishment PO of a given size when stock drops to or below a given reorder point. We code the logic relating these events into a program. We feed it with a random demand sequence (see bootstrapping above), run the program for a while, say one year of daily operations, compute performance metrics like Fill Rate and Average On Hand inventory, and “toss the dice” by re-running the program many times and averaging the results of many simulated years. The result is a good estimate of what happens when we make key management decisions: “If we set the reorder point at 10 units and the order quantity at 15 units, we can expect to get a service level of 89% and an average on hand of 21 units.” What the simulation is doing for us is exposing the consequences of management decisions based on realistic demand scenarios and solid math. The guesswork is gone.

Figure 2 shows some of the inner workings of a Monte Carlo simulation of an inventory system in four panels. The system uses a Min/Max inventory control policy with Min=10 and Max=25. No backorders are allowed: you have the good or you lose the business. Replenishment lead times are usually 7 days but sometimes 14. This simulation ran for one year.

The first panel shows a complex random demand scenario in which there is no demand on weekends, but demand generally increases each day from Monday to Friday. The second panel shows the random number of units on hand, which ebbs and flows with each replenishment cycle. The third panel shows the random sizes and timings of replenishment orders coming in from the supplier. The final panel shows the unsatisfied demand that jeopardizes customer relationships. This kind of detail can be very useful for building insight into the dynamics of an inventory system.

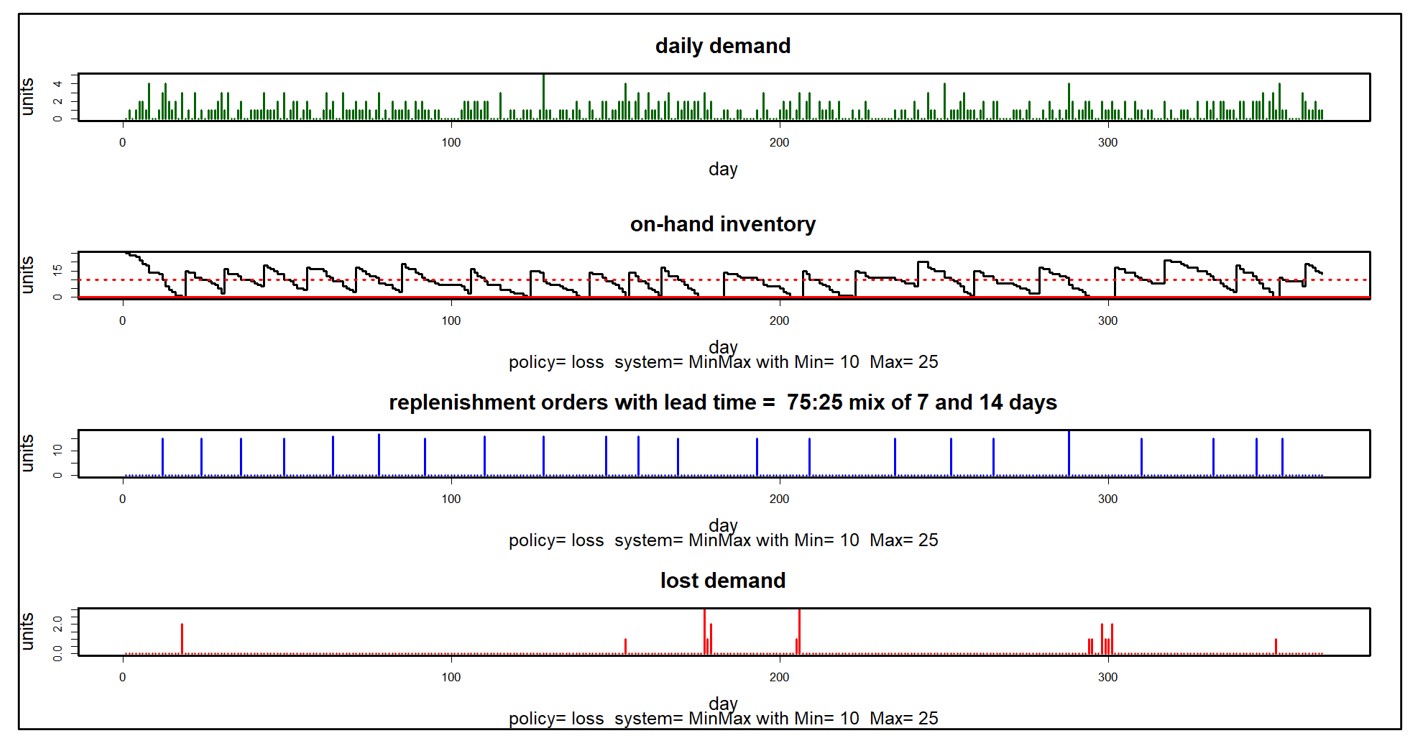
Figure 2: Details of a Monte Carlo simulation

Figure 2 shows only one of the countless ways that the year could play out. Generally, we want to average the results of many simulated years. After all, nobody would flip a coin once to decide if it were a fair coin. Figure 3 shows how four key performance metrics (KPI’s) vary from year to year for this system. Some metrics are relatively stable across simulations (Fill Rate), but others show more relative variability (Operating Cost= Holding Cost + Ordering Cost + Shortage Cost). Eyeballing the plots, we can estimate that the choices of Min=10, Max=25 leads to an average Operating cost of around $3,000 per year, a Fill Rate of around 90%, a Service Level of around 75%, and an Average On Hand of about 10

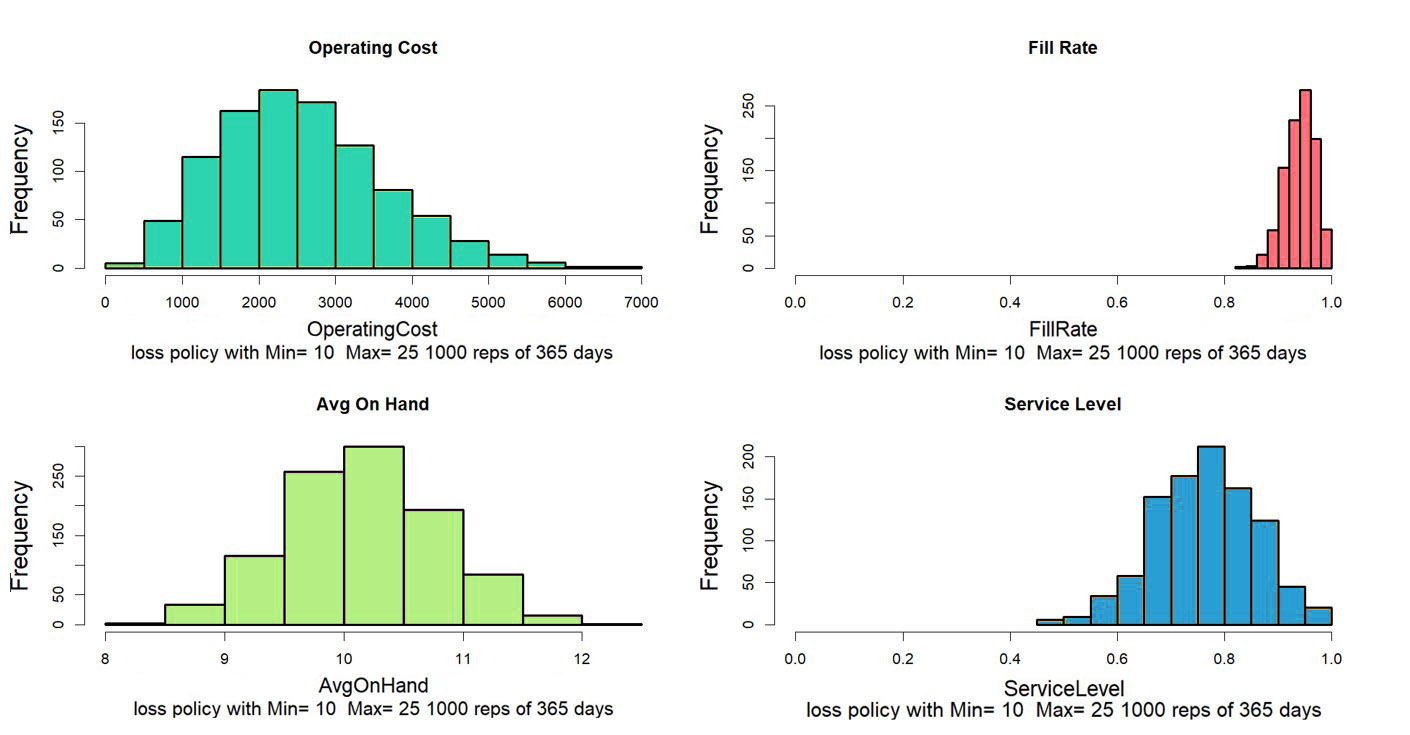
Figure 3: Variation in KPI’s computed over 1,000 simulated years

In fact, it is now possible to answer a higher level of management question. We can go beyond “What will happen if I do such-and-such?” to “What is the best thing I can do to achieve a fill rate of at least 90% for this item at the lowest possible cost?” The mathemagic  behind this leap is yet another key technology called “stochastic optimization”, but we’ll stop here for now. Suffice it to say that Smart’s SIO&P software can search the “design space” of Min and Max values to automatically find the best choice.

Reveal how forecasts are used with these 4 questions.

Often companies will insist that they “don’t use forecasts” to plan inventory.  They often use reorder point methods and are struggling to improve on-time delivery, inventory turns, and other KPIs. While they don’t think of what they are doing as explicitly forecasting, they certainly use estimates of future demand to develop reorder points such as min/max.

Regardless of what it is called, everyone tries to estimate future demand in some way and uses this estimate to set stocking policies and drive orders. To improve inventory planning and make sure you aren’t over/under ordering and creating large stockouts and inventory bloat, it is important to understand exactly how your organization uses forecasts. Once this is understood, you can assess whether the quality of the forecasts can be improved.

Try getting answers to the following questions. It will reveal how forecasts are being used in your business – even if you don’t think you use forecasts.

1.  Is your forecast a period-by-period estimate over time that is used to predict what on-hand inventory will be in the future and triggers order suggestions in your ERP system?

2. Or is your forecast used to derive a reorder point but not explicitly used as a per-period driver to trigger orders? Here, I may predict we’ll sell 10 per week based on the history, but we are not loading 10, 10, 10, 10, etc., into the ERP. Instead, I derive a reorder point or Min that covers the two-period lead time + some amount of buffer to help protect against stock out. In this case, I’ll order more when on hand gets to 25.

3. Is your forecast used as a guide for the planner to help subjectively determine when they should order more?  Here, I predict 10 per week, and I assess the on-hand inventory periodically, review the expected lead time, and I decide, given the 40 units I have on hand today, that I have “enough.” So, I do nothing now but will check back again in a week.

4. Is it used to set up blanket orders with suppliers? Here, I predict 10 per week and agree to a blanket purchase order with the supplier of 520 per year. The orders are then placed in advance to arrive in quantities of 10 once per week until the blanket order is consumed.

Once you get the answers, you can then ask how the estimates of demand are created.  Is it an average? Is it deriving demand over lead time from a sales forecast?  Is there a statistical forecast generated somewhere?  What methods are considered? It will also be important to assess how safety stocks are used to protect against demand and supply variability.  More on all of this in a future article.

​If you had your head up lately, you may have noticed some additional madness off the basketball court: The failure of Silicon Valley Bank. Those of us in the supply chain world may have dismissed the bank failure as somebody else’s problem, but that sorry episode holds a big lesson for us, too: The importance of stress testing done right.

The Washington Post recently carried an opinion piece by Natasha Sarin called “Regulators missed Silicon Valley Bank’s problems for months. Here’s why.” Sarin outlined the flaws in the stress testing regime imposed on the bank by the Federal Reserve. One problem is that the stress tests are too static. The Fed’s stress factor for nominal GDP growth was a single scenario listing presumed values over the next 13 quarters (see Figure 1). Those 13 quarterly projections might be somebody’s consensus view of what a bad hair day would look like, but that’s not the only way things could play out.  As a society, we are being taught to appreciate a better way to display contingencies every time the National Weather Service shows us projected hurricane tracks (see Figure 2). Each scenario represented by a different colored line shows a possible storm path, with the concentrated lines representing the most likely.  By exposing the lower probability paths, risk planning is improved.

When stress testing the supply chain, we need realistic scenarios of possible future demands that might occur, even extreme demands.   Smart provides this in our software (with considerable improvements in our Gen2 methods).  The software generates a huge number of credible demand scenarios, enough to expose the full scope of risks (see Figure 3). Stress testing is all about generating massive numbers of planning scenarios, and Smart’s probabilistic methods are a radical departure from previous deterministic S&OP applications, being entirely scenario based.

The other flaw in the Fed’s stress tests was that they were designed months in advance but never updated for changing conditions.  Demand planners and inventory managers intuitively appreciate that key variables like item demand and supplier lead time are not only highly random even when things are stable but also subject to abrupt shifts that should require rapid rewriting of planning scenarios (see Figure 4, where the average demand jumps up dramatically between observations 19 and 20). Smart’s Gen2 products include new tech for detecting such “regime changes”  and automatically changing scenarios accordingly.

Banks are forced to undergo stress tests, however flawed they may be, to protect their depositors. Supply chain professionals now have a way to protect their supply chains by using modern software to stress test their demand plans and inventory management decisions.

Figure 1: Scenarios used the Fed to stress test banks.

Figure 2: Scenarios used by the National Weather Service to predict hurricane tracks

Figure 3: Demand scenarios of the type generated by Smart Demand Planner

Figure 4: Example of regime change in product demand after observation #19

Whether you understand it in detail yourself or rely on trustworthy software, math is a fact of life for anyone in inventory management and demand forecasting who is hoping to remain competitive in the modern world.

At a conference recently, the lead presenter in an inventory management workshop proudly proclaimed that he had no need for “high-fallutin’ math”, which was explained to mean anything beyond sixth-grade math.

Math is not everyone’s first love. But if you really care about doing your job well, you can’t approach the work with a grade school mentality. Supply chain tasks like demand forecasting and inventory management are inherently mathematical. The blog associated with edX, a premier site for online college course material, has a great post on this topic, at https://www.mooc.org/blog/how-is-math-used-in-supply-chain. Let me quote the first bit:

Math and the supply chain go hand and hand. As supply chains grow, increasing complexity will drive companies to look for ways to manage large-scale decision-making. They can’t go back to how supply chains were 100 years ago—or even two years ago before the pandemic. Instead, new technologies will help streamline and manage the many moving parts. The logistics skills, optimization technologies, and organizational skills used in supply chain all require mathematics.

Our customers don’t need to be experts in supply chain math, they just need to be able to wield the software that contains the math. Software combines users’ experience and subject matter expertise to produce results that make the difference between success and failure. To do its job, the software can’t stop at sixth-grade math; it needs probability, statistics, and optimization theory.

It’s up to us software vendors to package the math in such a way that what goes into the calculations is all that is relevant, even if complicated; and that what comes out is clear, decision-relevant, and defensible when you must justify your recommendations to higher management.

Sixth-grade math can’t warn you when the way you propose to manage a critical spare part will mean a 70% chance of falling short of your item availability target. It can’t tell you how best to adjust your reorder points when a supplier calls and says, “We have a delivery problem.” It can’t save your skin when there is a surprisingly large order and you have to quickly figure out the best way to set up some expedited special orders without busting the operating budget.

So, respect the folk wisdom and don’t bring a knife to a gunfight.