Feynman’s perspective illuminates our journey: “In its efforts to learn as much as possible about nature, modern physics has found that certain things can never be “known” with certainty. Much of our knowledge must always remain uncertain. The most we can know is in terms of probabilities.” ― Richard Feynman, The Feynman Lectures on Physics.
When we try to understand the complex world of logistics, randomness plays a pivotal role. This introduces an interesting paradox: In a reality where precision and certainty are prized, could the unpredictable nature of supply and demand actually serve as a strategic ally?
The quest for accurate forecasts is not just an academic exercise; it’s a critical component of operational success across numerous industries. For demand planners who must anticipate product demand, the ramifications of getting it right—or wrong—are critical. Hence, recognizing and harnessing the power of randomness isn’t merely a theoretical exercise; it’s a necessity for resilience and adaptability in an ever-changing environment.
Embracing Uncertainty: Dynamic, Stochastic, and Monte Carlo Methods
Dynamic Modeling: The quest for absolute precision in forecasts ignores the intrinsic unpredictability of the world. Traditional forecasting methods, with their rigid frameworks, fall short in accommodating the dynamism of real-world phenomena. By embracing uncertainty, we can pivot towards more agile and dynamic models that incorporate randomness as a fundamental component. Unlike their rigid predecessors, these models are designed to evolve in response to new data, ensuring resilience and adaptability. This paradigm shift from a deterministic to a probabilistic approach enables organizations to navigate uncertainty with greater confidence, making informed decisions even in volatile environments.
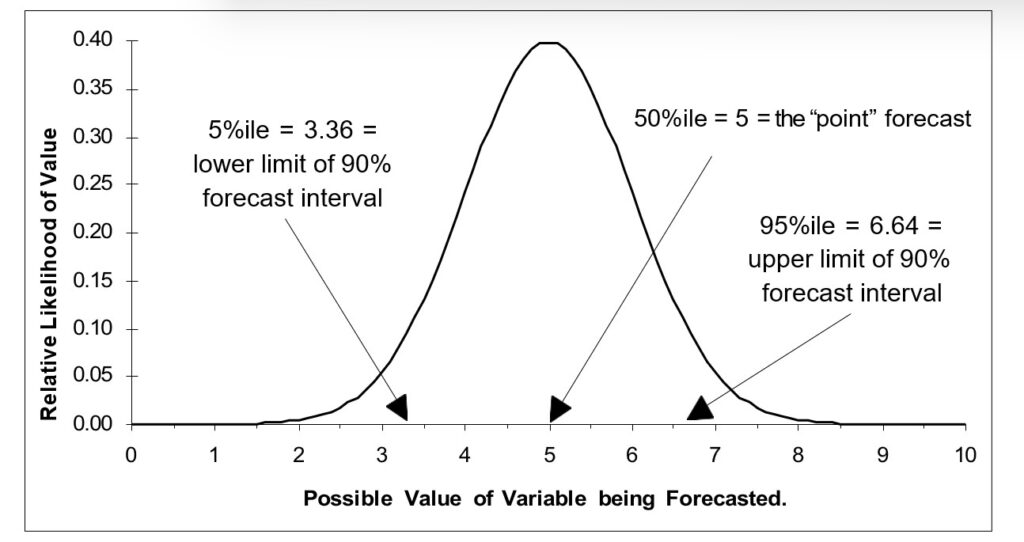
Stochastic modeling guides forecasters through the fog of unpredictability with the principles of probability. Far from attempting to eliminate randomness, stochastic models embrace it. These models eschew the notion of a singular, predetermined future, presenting instead an array of possible outcomes, each with its estimated probability. This approach offers a more nuanced and realistic representation of the future, acknowledging the inherent variability of systems and processes. By mapping out a spectrum of potential futures, stochastic modeling equips decision-makers with a comprehensive understanding of uncertainty, enabling strategic planning that is both informed and flexible.
Named after the historical hub of chance and fortune, Monte Carlo simulations harness the power of randomness to explore the vast landscape of possible outcomes. This technique involves the generation of thousands, if not millions, of scenarios through random sampling, each scenario painting a different picture of the future based on the inherent uncertainties of the real world. Decision-makers, armed with insights from Monte Carlo simulations, can gauge the range of possible impacts of their decisions, making it an invaluable tool for risk assessment and strategic planning in uncertain environments.
Real-World Successes: Harnessing Randomness
The strategy of integrating randomness into forecasting has proven invaluable across diverse sectors. For instance, major investment firms and banks constantly rely on stochastic models to cope with the volatile behavior of the stock market. A notable example is how hedge funds employ these models to predict price movements and manage risk, leading to more strategic investment choices.
Similarly, in supply chain management, many companies rely on Monte Carlo simulations to tackle the unpredictability of demand, especially during peak seasons like the holidays. By simulating various scenarios, they can prepare for a range of outcomes, ensuring that they have adequate stock levels without overcommitting resources. This approach minimizes the risk of both stockouts and excess inventory.
These real-world successes highlight the value of integrating randomness into forecasting endeavors. Far from being the adversary it’s often perceived to be, randomness emerges as an indispensable ally in the intricate ballet of forecasting. By adopting methods that honor the inherent uncertainty of the future—bolstered by advanced tools like Smart IP&O—organizations can navigate the unpredictable with confidence and agility. Thus, in the grand scheme of forecasting, it may be wise to embrace the notion that while we cannot control the roll of the dice, we can certainly strategize around it.