Nauwkeurigheid van prognoses is een belangrijke maatstaf om de kwaliteit van uw vraagplanningsproces te beoordelen. (Het is niet de enige. Anderen omvatten tijdigheid en kosten; zie 5 Tips voor vraagplanning voor het berekenen van prognoseonzekerheid.) Zodra u prognoses heeft, zijn er een aantal manieren om hun nauwkeurigheid samen te vatten, meestal aangeduid met obscure drie- of vierletterige acroniemen zoals MAPE, RMSE en MAE. Zien Vier handige manieren om prognosefouten te meten voor meer informatie.
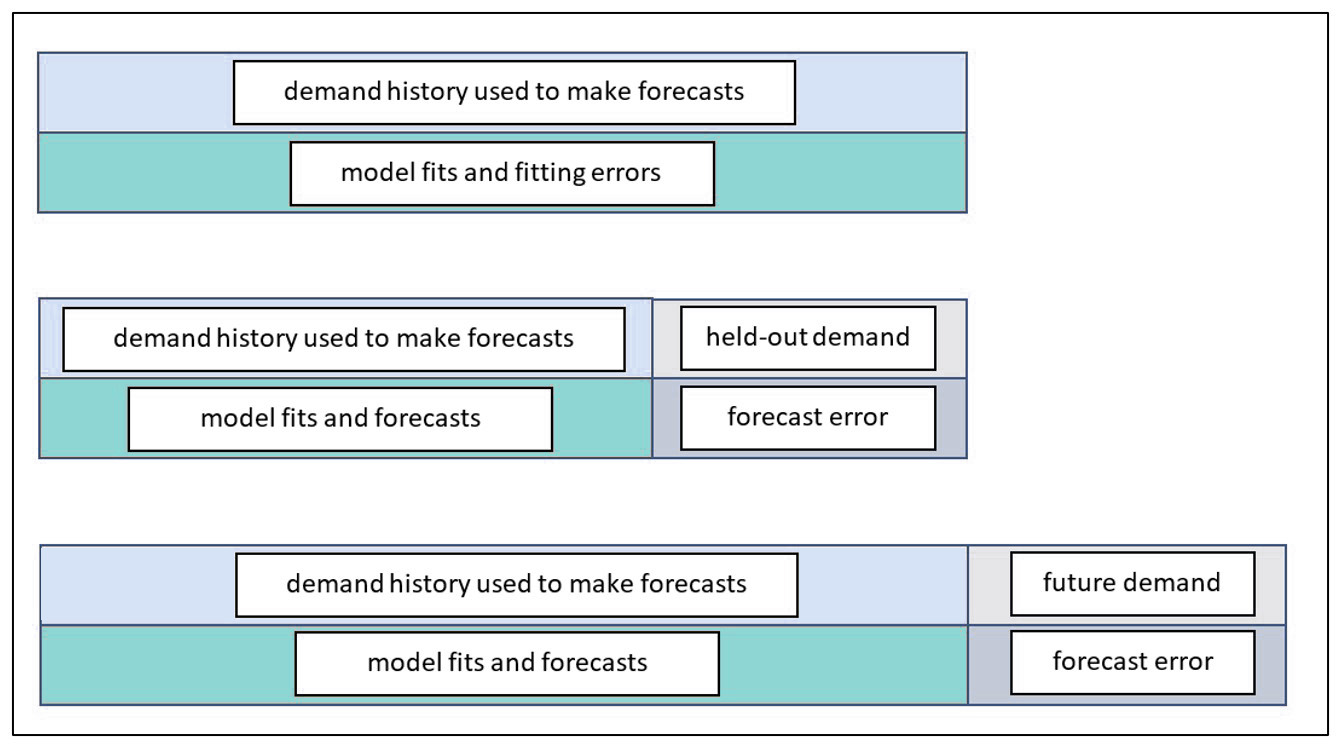
Een minder besproken maar meer fundamentele kwestie is hoe computationele experimenten worden georganiseerd voor het berekenen van voorspellingsfouten. Deze post vergelijkt de drie belangrijkste experimentele ontwerpen. Een van hen is ouderwets en komt in wezen neer op valsspelen. Een andere is de gouden standaard. Een derde is een handig hulpmiddel dat de gouden standaard nabootst en kan het beste worden gezien als een voorspelling van hoe de gouden standaard zal uitpakken. Figuur 1 is een schematische weergave van de drie methoden.
Afbeelding 1: Drie manieren om prognosefouten te beoordelen
Het bovenste paneel van figuur 1 geeft de manier weer waarop voorspellingsfouten werden beoordeeld in het begin van de jaren '80 voordat we de stand van de techniek verplaatsten naar het schema in het middelste paneel. Vroeger werden prognoses beoordeeld op dezelfde gegevens die werden gebruikt om de prognoses te berekenen. Nadat een model aan de gegevens was aangepast, waren de berekende fouten niet voor modelvoorspellingen maar voor model past bij. Het verschil is dat prognoses voor toekomstige waarden zijn, terwijl aanpassingen voor gelijktijdige waarden zijn. Stel dat het voorspellingsmodel een eenvoudig voortschrijdend gemiddelde is van de drie meest recente waarnemingen. Op tijdstip 3 berekent het model het gemiddelde van waarnemingen 1, 2 en 3. Dit gemiddelde wordt dan vergeleken met de waargenomen waarde op tijdstip 3. We noemen dit vals spelen omdat de waargenomen waarde op tijdstip 3 een stem kreeg over wat de voorspelling zou moeten zijn op tijdstip 3. Een echte prognosebeoordeling zou het gemiddelde van de eerste drie waarnemingen vergelijken met de waarde van de volgende, vierde, observatie. Anders blijft de voorspeller achter met een te optimistische beoordeling van de nauwkeurigheid van de voorspelling.
Het onderste paneel van figuur 1 toont de beste manier om de nauwkeurigheid van prognoses te beoordelen. In dit schema worden alle historische vraaggegevens gebruikt om in een model te passen, dat vervolgens wordt gebruikt om toekomstige, onbekende vraagwaarden te voorspellen. Uiteindelijk ontvouwt de toekomst zich, onthullen de werkelijke toekomstige waarden zich en kunnen werkelijke voorspellingsfouten worden berekend. Dit is de gouden standaard. Deze informatie wordt ingevuld in het rapport 'Prognoses versus actuals' in onze software.
Het middelste paneel toont een handige tussenmaat. Het probleem met de gouden standaard is dat u moet wachten om erachter te komen hoe goed de door u gekozen prognosemethoden presteren. Deze vertraging helpt niet wanneer u op dit moment moet kiezen welke prognosemethode u voor elk item wilt gebruiken. Het geeft ook geen tijdige inschatting van de prognoseonzekerheid die u zult ervaren, wat belangrijk is voor risicobeheer zoals het afdekken van prognoses. De middenweg is gebaseerd op hold-out-analyse, die de meest recente waarnemingen uitsluit (“holds out”) en de voorspellingsmethode vraagt zijn werk te doen zonder die grondwaarheden te kennen. Vervolgens kunnen de prognoses op basis van de verkorte vraaggeschiedenis worden vergeleken met de uitgestelde werkelijke waarden om een eerlijke beoordeling van de prognosefout te krijgen.