Vraagplanning kost tijd en moeite. Het is de moeite waard voor zover het je daadwerkelijk helpt te maken wat je nodig hebt wanneer je het nodig hebt.

Maar het werk kan goed of slecht worden gedaan. We zien veel fabrikanten stoppen bij het eerste niveau terwijl ze gemakkelijk naar het tweede niveau kunnen gaan. En met een beetje meer moeite zouden ze helemaal naar het derde niveau kunnen gaan, door gebruik te maken van probabilistische modellering om de resultaten van de vraagplanning om te zetten in een voorraadoptimalisatieproces.

Het eerste niveau

Het eerste niveau is het maken van een vraagprognose met behulp van statistische methoden. Afbeelding 1 toont een poging op het eerste niveau: de vraaggeschiedenis van een artikel (rode lijn) en de verwachte prognose voor 12 maanden (groene lijn).

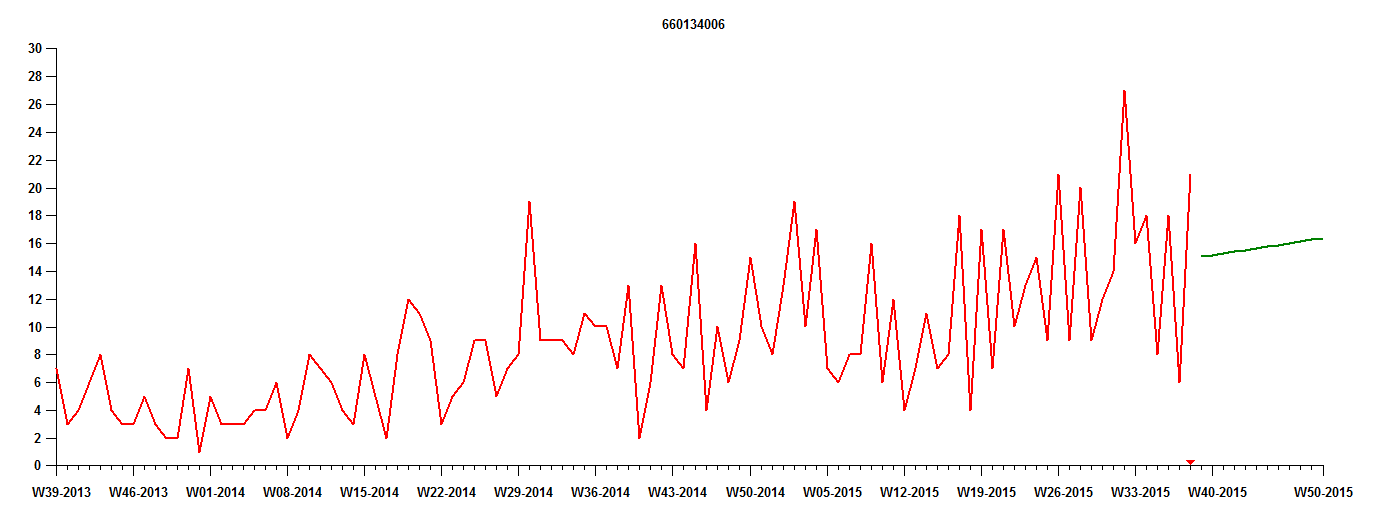
De voorspelling is kaal. Het projecteert alleen verwacht vraag negeren dat de vraag volatiel is en onvermijdelijk prognosefouten zal veroorzaken. (Dit is nog een voorbeeld van een belangrijke stelregel: “Het gemiddelde is niet het antwoord”). De voorspelling is waarschijnlijk zowel te hoog als te laag, en er is geen indicatie van voorspellingsonzekerheid bij de voorspelling. Dit betekent dat de planner geen inschatting heeft van het risico dat gepaard gaat met het nakomen van de prognose. Toch biedt deze prognose een rationele basis voor productieplanning, persoonlijke planning en inkoop van grondstoffen. Het is dus veel beter dan gissen.

Het tweede niveau

Het tweede niveau houdt expliciet rekening met de voorspelde onzekerheid. Figuur 2 toont een inspanning van het tweede niveau, bekend als een "percentielprognose".

Nu zien we een expliciete indicatie van voorspelde onzekerheid. De cyaankleurige lijn boven de groene prognoselijn vertegenwoordigt het verwachte 90e percentiel van de maandelijkse vraag. Dat wil zeggen, de vraag in elke toekomstige maand heeft een kans van 90% om op of onder de cyaanlijn te vallen. Anders gezegd, er is een kans van 10% dat de vraag elke maand de cyaanlijn overschrijdt.

Deze analyse is veel nuttiger omdat het risicobeheer ondersteunt. Als het belangrijk is om voldoende aanvoer van dit artikel te verzekeren, dan is het logisch om te produceren tot het 90e percentiel in plaats van tot de verwachte prognose. Het is tenslotte een gok of de verwachte voorspelling zal resulteren in voldoende productie om aan de maandelijkse vraag te voldoen. Deze prognose op het tweede niveau is in feite een ruwe vervanging van een zorgvuldig voorraadbeheerproces.

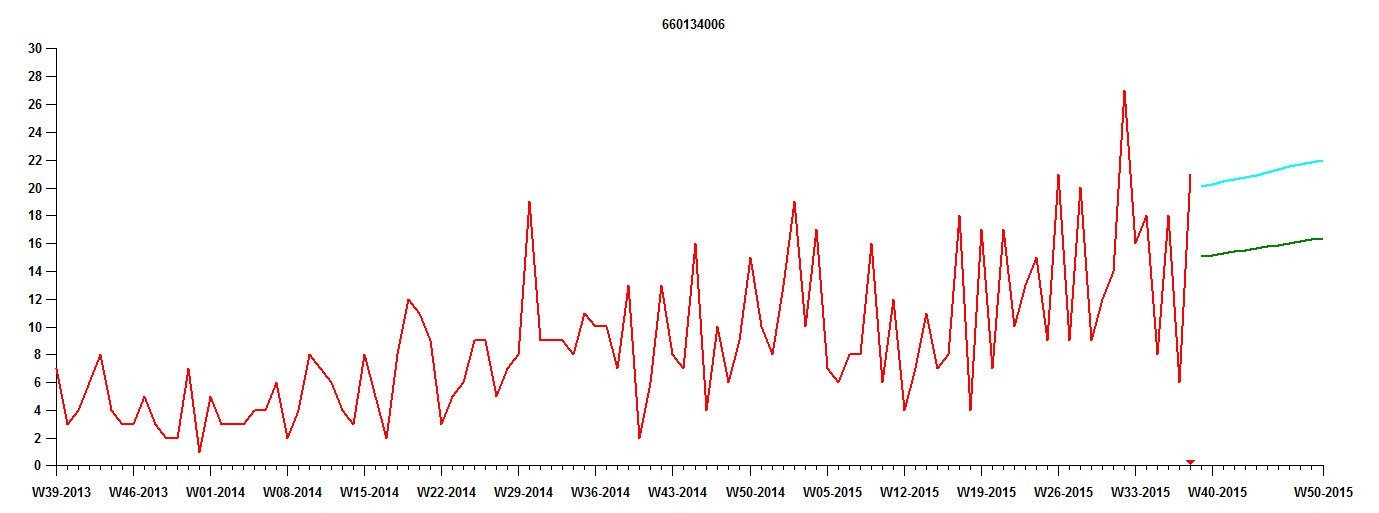
Afbeelding 2. Een percentielprognose, waarbij de cyaankleurige lijn het 90e percentiel van de maandelijkse vraag schat.

Gaat helemaal naar het derde niveau

Best practice is het derde niveau, dat vraagplanning gebruikt als basis voor het voltooien van een tweede taak: expliciete voorraadoptimalisatie. Figuur 3 toont de fundamentele plot voor het efficiënte beheer van ons eindproduct, ervan uitgaande dat het een productietijd van 1 maand heeft.

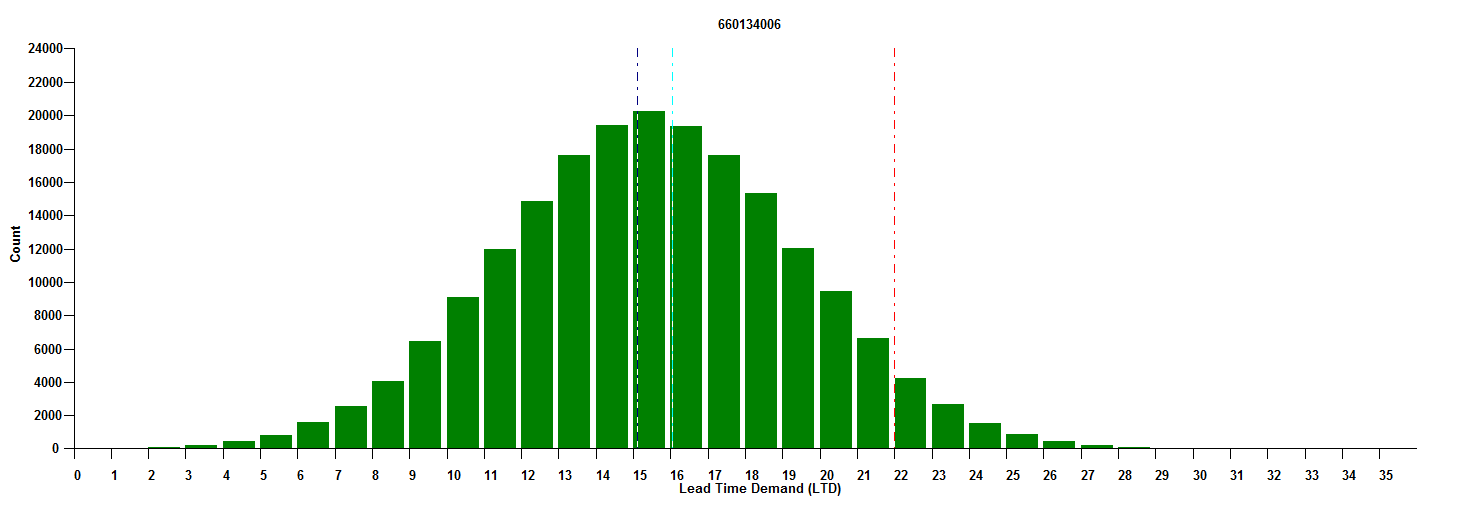
Afbeelding 3 toont het gebruik van probabilistische prognoses en hoeveel afname van de voorraad gereed product kan plaatsvinden gedurende een productietijd van een maand. De onzekerheid in de vraag komt tot uiting in de spreiding van de mogelijke vraag, van een dieptepunt van 0 tot een maximum van 35, waarbij 15 eenheden de meest waarschijnlijke waarde is. De verticale rode lijn bij 22 geeft het "bestelpunt" (of "min" of "triggerwaarde") aan dat overeenkomt met het behouden van de kans op voorraad in afwachting van aanvulling tot een lage 5%. Wanneer de voorraad daalt tot 22 of lager, is het tijd om meer te bestellen. Het derde niveau maakt gebruik van probabilistische vraagprognoses met volledige blootstelling aan prognoseonzekerheid om de voorraad van het eindproduct efficiënt te beheren.

Opsommen

Het voorspellen van de meest waarschijnlijke vraag naar een artikel is een nuttige eerste stap. Het brengt je halverwege waar je wilt zijn. Maar het biedt een onvolledige gids voor planning, omdat het de volatiliteit van de vraag en de verwachte onzekerheid die het creëert, negeert. Door een buffer aan de vraagprognose toe te voegen, komt u verder, omdat het risico wordt verkleind dat een sprong in de vraag u een tekort aan product zal opleveren. Dit kussen kan worden berekend door middel van probabilistische prognosebenaderingen die een hoog percentage van de verdeling van de toekomstige vraag voorspellen. En als u nog een stap verder wilt gaan, kunt u prognoses van de vraagverdeling over een doorlooptijd invoeren om bestelpunten (minuten) te berekenen om ervoor te zorgen dat u een acceptabel laag risico op voorraaduitval heeft.

Gezien wat moderne prognosetechnologie voor u kan doen, waarom zou u halverwege uw doel willen stoppen?