Vraagplanning kost tijd en moeite. Het is de moeite waard voor zover het je daadwerkelijk helpt te maken wat je nodig hebt wanneer je het nodig hebt.
Maar het werk kan goed of slecht worden gedaan. We zien veel fabrikanten stoppen bij het eerste niveau terwijl ze gemakkelijk naar het tweede niveau kunnen gaan. En met een beetje meer moeite zouden ze helemaal naar het derde niveau kunnen gaan, door gebruik te maken van probabilistische modellering om de resultaten van de vraagplanning om te zetten in een voorraadoptimalisatieproces.
Het eerste niveau
Het eerste niveau is het maken van een vraagprognose met behulp van statistische methoden. Afbeelding 1 toont een poging op het eerste niveau: de vraaggeschiedenis van een artikel (rode lijn) en de verwachte prognose voor 12 maanden (groene lijn).
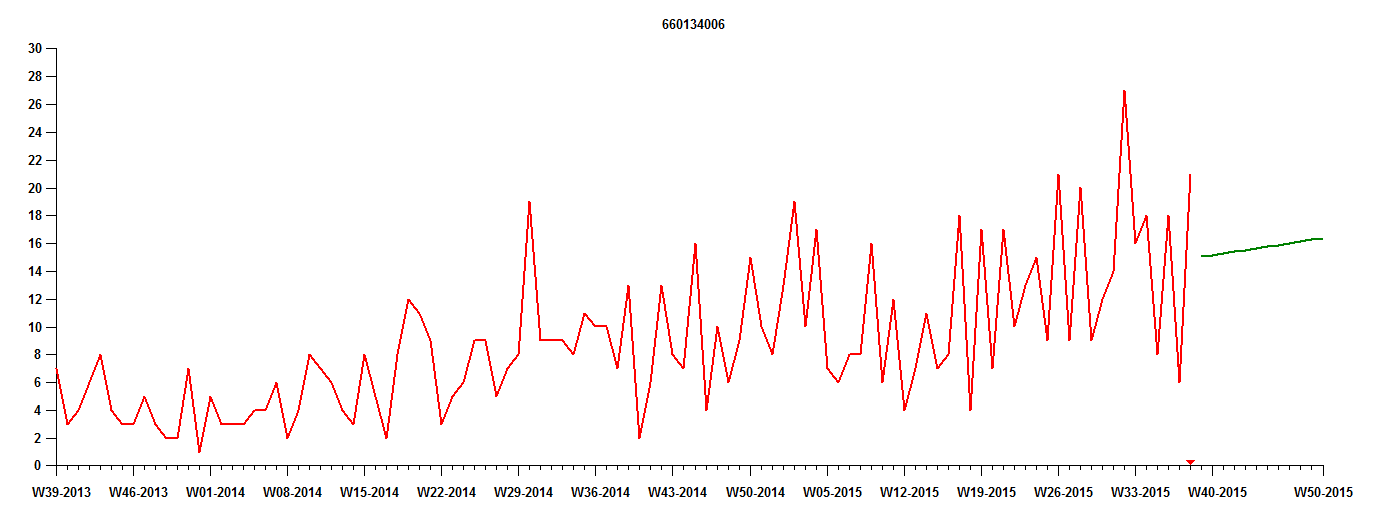
De voorspelling is kaal. Het projecteert alleen verwacht vraag negeren dat de vraag volatiel is en onvermijdelijk prognosefouten zal veroorzaken. (Dit is nog een voorbeeld van een belangrijke stelregel: “Het gemiddelde is niet het antwoord”). De voorspelling is waarschijnlijk zowel te hoog als te laag, en er is geen indicatie van voorspellingsonzekerheid bij de voorspelling. Dit betekent dat de planner geen inschatting heeft van het risico dat gepaard gaat met het nakomen van de prognose. Toch biedt deze prognose een rationele basis voor productieplanning, persoonlijke planning en inkoop van grondstoffen. Het is dus veel beter dan gissen.
Het tweede niveau
Het tweede niveau houdt expliciet rekening met de voorspelde onzekerheid. Figuur 2 toont een inspanning van het tweede niveau, bekend als een "percentielprognose".
Nu zien we een expliciete indicatie van voorspelde onzekerheid. De cyaankleurige lijn boven de groene prognoselijn vertegenwoordigt het verwachte 90e percentiel van de maandelijkse vraag. Dat wil zeggen, de vraag in elke toekomstige maand heeft een kans van 90% om op of onder de cyaanlijn te vallen. Anders gezegd, er is een kans van 10% dat de vraag elke maand de cyaanlijn overschrijdt.
Deze analyse is veel nuttiger omdat het risicobeheer ondersteunt. Als het belangrijk is om voldoende aanvoer van dit artikel te verzekeren, dan is het logisch om te produceren tot het 90e percentiel in plaats van tot de verwachte prognose. Het is tenslotte een gok of de verwachte voorspelling zal resulteren in voldoende productie om aan de maandelijkse vraag te voldoen. Deze prognose op het tweede niveau is in feite een ruwe vervanging van een zorgvuldig voorraadbeheerproces.
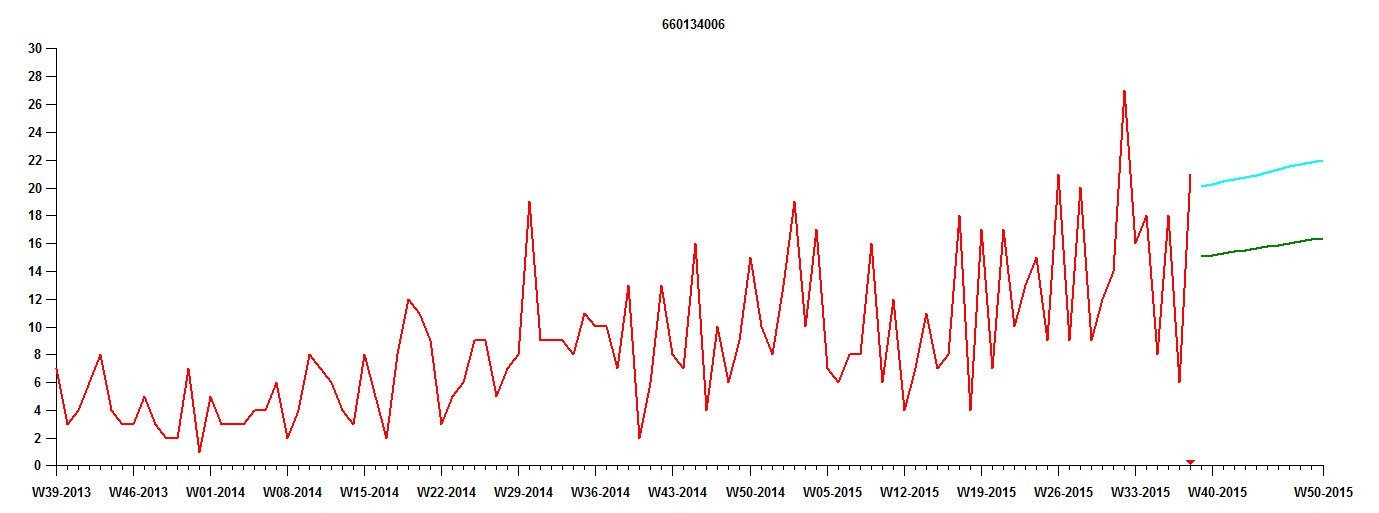
Afbeelding 2. Een percentielprognose, waarbij de cyaankleurige lijn het 90e percentiel van de maandelijkse vraag schat.
Gaat helemaal naar het derde niveau
Best practice is het derde niveau, dat vraagplanning gebruikt als basis voor het voltooien van een tweede taak: expliciete voorraadoptimalisatie. Figuur 3 toont de fundamentele plot voor het efficiënte beheer van ons eindproduct, ervan uitgaande dat het een productietijd van 1 maand heeft.
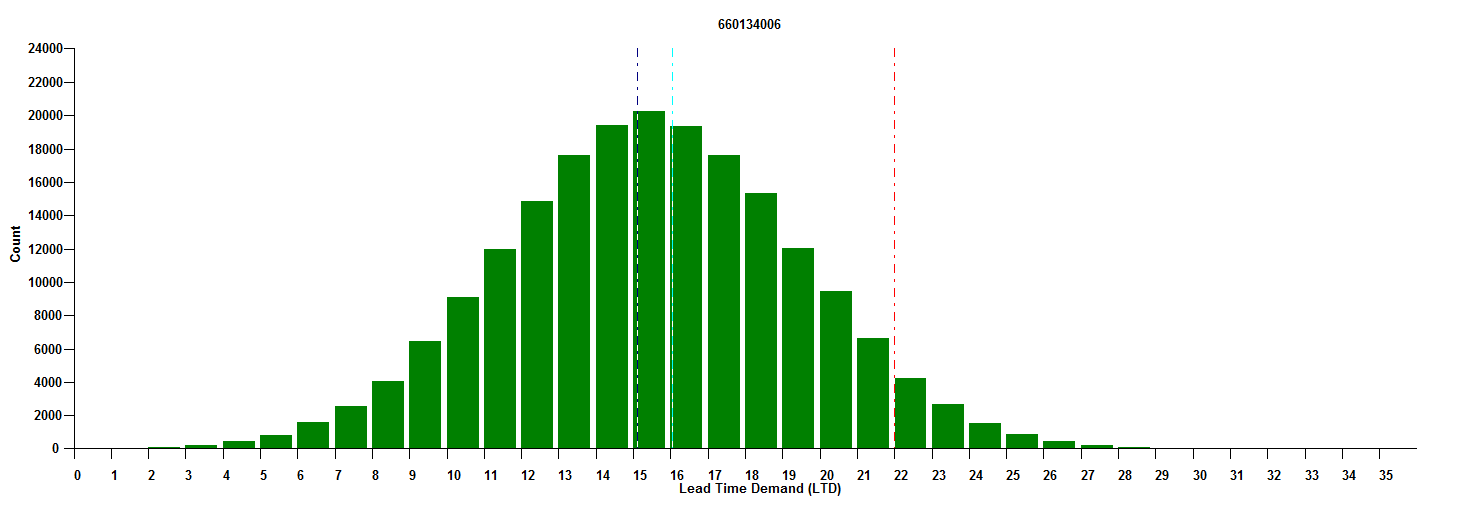
Afbeelding 3 toont het gebruik van probabilistische prognoses en hoeveel afname van de voorraad gereed product kan plaatsvinden gedurende een productietijd van een maand. De onzekerheid in de vraag komt tot uiting in de spreiding van de mogelijke vraag, van een dieptepunt van 0 tot een maximum van 35, waarbij 15 eenheden de meest waarschijnlijke waarde is. De verticale rode lijn bij 22 geeft het "bestelpunt" (of "min" of "triggerwaarde") aan dat overeenkomt met het behouden van de kans op voorraad in afwachting van aanvulling tot een lage 5%. Wanneer de voorraad daalt tot 22 of lager, is het tijd om meer te bestellen. Het derde niveau maakt gebruik van probabilistische vraagprognoses met volledige blootstelling aan prognoseonzekerheid om de voorraad van het eindproduct efficiënt te beheren.
Opsommen
Het voorspellen van de meest waarschijnlijke vraag naar een artikel is een nuttige eerste stap. Het brengt je halverwege waar je wilt zijn. Maar het biedt een onvolledige gids voor planning, omdat het de volatiliteit van de vraag en de verwachte onzekerheid die het creëert, negeert. Door een buffer aan de vraagprognose toe te voegen, komt u verder, omdat het risico wordt verkleind dat een sprong in de vraag u een tekort aan product zal opleveren. Dit kussen kan worden berekend door middel van probabilistische prognosebenaderingen die een hoog percentage van de verdeling van de toekomstige vraag voorspellen. En als u nog een stap verder wilt gaan, kunt u prognoses van de vraagverdeling over een doorlooptijd invoeren om bestelpunten (minuten) te berekenen om ervoor te zorgen dat u een acceptabel laag risico op voorraaduitval heeft.
Gezien wat moderne prognosetechnologie voor u kan doen, waarom zou u halverwege uw doel willen stoppen?
gerelateerde berichten

6 essentiële stappen voor een betere herstelplanning
Nu we het middelpunt in 2013 naderen, is er nog steeds veel economische onzekerheid die uw planningsprocessen voor de toeleveringsketen bemoeilijkt. Sommigen kijken naar deze wankele economie en stellen noodzakelijke investeringen uit die hun organisaties kunnen positioneren voor een sterke toekomst.
Aanbevolen literatuur: uitmuntendheid in vraagplanning
In een recente post bij SupplyChainBrain kijkt Robert Bowman naar excellentie in vraagplanning. Gefocust op bewonderenswaardige kwaliteiten en technieken, zou het interessant moeten zijn voor elke vraagplanner die zijn of haar vak wil verbeteren.

Helden van disruptieve innovatie
De executive suites bij de meeste bedrijven worden bevolkt door leiders die zakelijke 'helden' zijn geworden. Deze uitzonderlijke presteerders leidden - en leiden nog steeds - transformatieve initiatieven die omzetgroei stimuleren, kosten verlagen en aandeelhouderswaarde vergroten.












 Wat positieve scheefheid een probleem maakt, is dat het de opvullingsgraad van een item verlaagt. Opvullingspercentage is belangrijk
Wat positieve scheefheid een probleem maakt, is dat het de opvullingsgraad van een item verlaagt. Opvullingspercentage is belangrijk 











 Een ander voordeel van dit boek is de selectie van onderwerpen. De technische zijn redelijk standaard (afvlakkingsmethoden, regressie met behulp van polynoomtrends en dummy-variabelen), maar variëren ook een beetje in de richting van meer exotisch (logistische regressie, neurale netwerken, een beetje ARIMA). Indrukwekkender is de opname van wat "meta-onderwerpen" kunnen worden genoemd die relevant zijn voor prognoses: prestatiebeoordeling, een overzicht van alternatieve technische benaderingen en een over het prognoseproces, van het definiëren van doelen tot manieren om rapporten anders af te stemmen op management- en technische publiek. Dit is het soort voorspellende wijsheid die we vinden
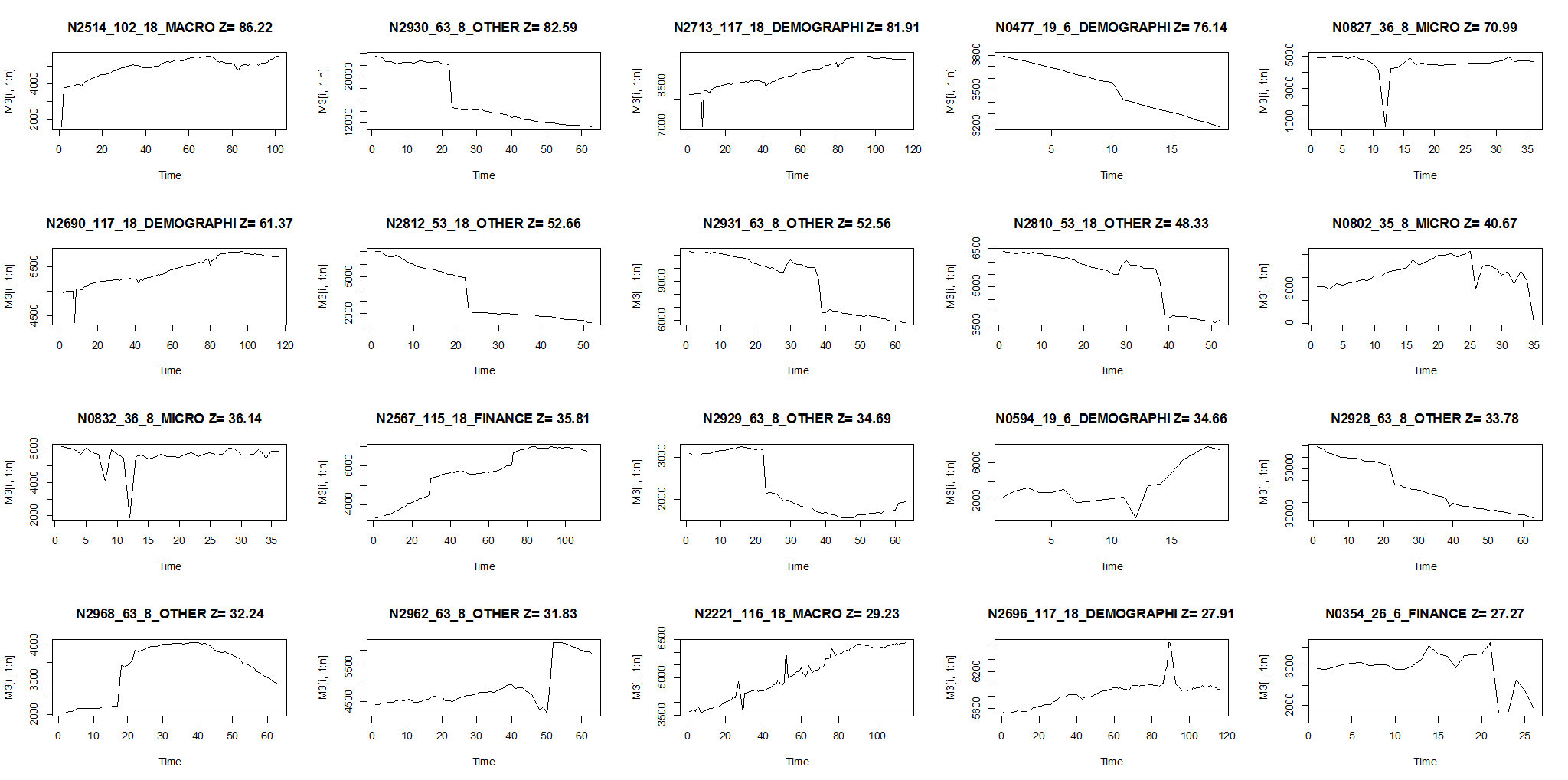
Een ander voordeel van dit boek is de selectie van onderwerpen. De technische zijn redelijk standaard (afvlakkingsmethoden, regressie met behulp van polynoomtrends en dummy-variabelen), maar variëren ook een beetje in de richting van meer exotisch (logistische regressie, neurale netwerken, een beetje ARIMA). Indrukwekkender is de opname van wat "meta-onderwerpen" kunnen worden genoemd die relevant zijn voor prognoses: prestatiebeoordeling, een overzicht van alternatieve technische benaderingen en een over het prognoseproces, van het definiëren van doelen tot manieren om rapporten anders af te stemmen op management- en technische publiek. Dit is het soort voorspellende wijsheid die we vinden 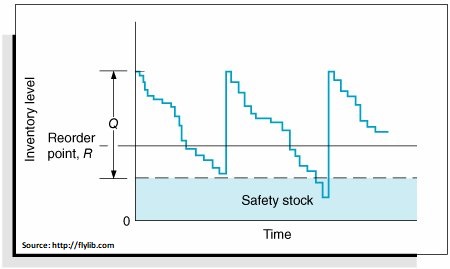 In meer technische details: de prognosefouten die worden geschat door dit glijdende simulatieproces geven het niveau van onzekerheid aan. We gebruiken deze fouten om de standaarddeviatie van de prognoses te schatten. Nu, met een regelmatige vraag, kunnen we aannemen dat de voorspellingen (die schattingen zijn van toekomstig gedrag) het beste worden weergegeven door een klokvormige kansverdeling - wat statistici de "normale verdeling" noemen. Het centrum van die verdeling is onze puntvoorspelling. De breedte van die verdeling is de standaarddeviatie van de "glijdende simulatie"-voorspelling van de bekende werkelijke waarden - we halen dit rechtstreeks uit onze schattingen van de voorspellingsfout.
In meer technische details: de prognosefouten die worden geschat door dit glijdende simulatieproces geven het niveau van onzekerheid aan. We gebruiken deze fouten om de standaarddeviatie van de prognoses te schatten. Nu, met een regelmatige vraag, kunnen we aannemen dat de voorspellingen (die schattingen zijn van toekomstig gedrag) het beste worden weergegeven door een klokvormige kansverdeling - wat statistici de "normale verdeling" noemen. Het centrum van die verdeling is onze puntvoorspelling. De breedte van die verdeling is de standaarddeviatie van de "glijdende simulatie"-voorspelling van de bekende werkelijke waarden - we halen dit rechtstreeks uit onze schattingen van de voorspellingsfout.