Resumen
El análisis avanzado de la cadena de suministro de Smart Software explota múltiples métodos avanzados. Dos de los más importantes son el “bootstrapping estadístico” y la “simulación Monte Carlo”. Dado que ambos involucran muchos números aleatorios que vuelan, la gente a veces se confunde acerca de cuál es cuál y para qué sirven. Por eso, esta nota. En pocas palabras: el arranque estadístico genera escenarios de demanda para la previsión. La simulación de Monte Carlo utiliza los escenarios para la optimización del inventario.
arranque
Bootstrapping, también llamado "remuestreo", es un método de estadísticas computacionales que utilizamos para crear escenarios de demanda para la previsión. La esencia del problema de pronóstico es exponer los posibles futuros que su empresa podría enfrentar para que pueda averiguar cómo administrar los riesgos comerciales. Los métodos de pronóstico tradicionales se enfocan en calcular los futuros "más probables", pero no llegan a presentar el panorama completo del riesgo. Bootstrapping proporciona un número ilimitado de escenarios hipotéticos realistas.
Bootstrapping hace esto sin hacer suposiciones poco realistas sobre la demanda, es decir, que no es intermitente o que tiene una distribución de tamaños en forma de campana. Esas suposiciones son muletas para simplificar las matemáticas, pero el arranque es un procedimiento, no una ecuación, por lo que no necesita tales simplificaciones.
Para el tipo de demanda más simple, que es una aleatoriedad estable sin estacionalidad ni tendencia, el arranque es muy fácil. Para tener una idea razonable de cuál podría ser el valor de una sola demanda futura, elija una de las demandas históricas al azar. Para crear un escenario de demanda, haga múltiples selecciones aleatorias del pasado y únalas. Hecho. Es posible agregar un poco más de realismo "variando" los valores de demanda, es decir, agregando o restando un poco de aleatoriedad adicional a cada uno, pero incluso eso es simple.
La figura 1 muestra un arranque simple. La primera línea es una secuencia corta de la demanda histórica de un SKU. Las siguientes líneas muestran escenarios de demanda futura creados al seleccionar aleatoriamente valores del historial de demanda. Por ejemplo, las siguientes tres demandas pueden ser (0, 14, 6), o (2, 3, 5), etc.
Las operaciones de mayor frecuencia, como los pronósticos diarios, traen consigo patrones de demanda más complejos, como la doble estacionalidad (p. ej., día de la semana y mes del año) y/o tendencia. Esto nos desafió a inventar una nueva generación de algoritmos de arranque. Recientemente obtuvimos una patente de EE. UU. para este avance, pero la esencia es la descrita anteriormente.
Simulación del Monte Carlo
Montecarlo es famoso por sus casinos que, al igual que el bootstrapping, invocan la idea de la aleatoriedad. Los métodos de Monte Carlo se remontan a mucho tiempo atrás, pero el ímpetu moderno vino con la necesidad de hacer algunos cálculos peludos sobre dónde volarían los neutrones cuando explota una bomba atómica.
La esencia del análisis de Monte Carlo es esta: “Nuestro problema es demasiado complicado para analizarlo con ecuaciones de papel y lápiz. Entonces, escribamos un programa de computadora que codifique los pasos individuales del proceso, coloque los elementos aleatorios (por ejemplo, en qué dirección se dispara un neutrón), déle cuerda y observe cómo funciona. Dado que hay mucha aleatoriedad, ejecutemos el programa un millón de veces y promediemos los resultados”.
Al aplicar este enfoque a la gestión de inventario, tenemos un conjunto diferente de eventos que ocurren aleatoriamente: por ejemplo, una demanda de un tamaño determinado llega un día aleatorio, un reabastecimiento de un tamaño determinado llega después de un tiempo de espera aleatorio, recortamos un PO de reabastecimiento de un tamaño determinado cuando las existencias caen hasta un punto de pedido determinado o por debajo de él. Codificamos la lógica que relaciona estos eventos en un programa. Lo alimentamos con una secuencia de demanda aleatoria (consulte el arranque anterior), ejecutamos el programa durante un tiempo, digamos un año de operaciones diarias, calculamos métricas de rendimiento como Tasa de llenado y Promedio de inventario disponible, y "tiramos los dados" volviendo a ejecutar el programa muchas veces y promediando los resultados de muchos años simulados. El resultado es una buena estimación de lo que sucede cuando tomamos decisiones gerenciales clave: “Si establecemos el punto de reorden en 10 unidades y la cantidad de la orden en 15 unidades, podemos esperar obtener un nivel de servicio de 89% y un promedio disponible de 21 unidades.” Lo que la simulación está haciendo por nosotros es exponer las consecuencias de las decisiones de gestión basadas en escenarios de demanda realistas y matemáticas sólidas. Las conjeturas se han ido.
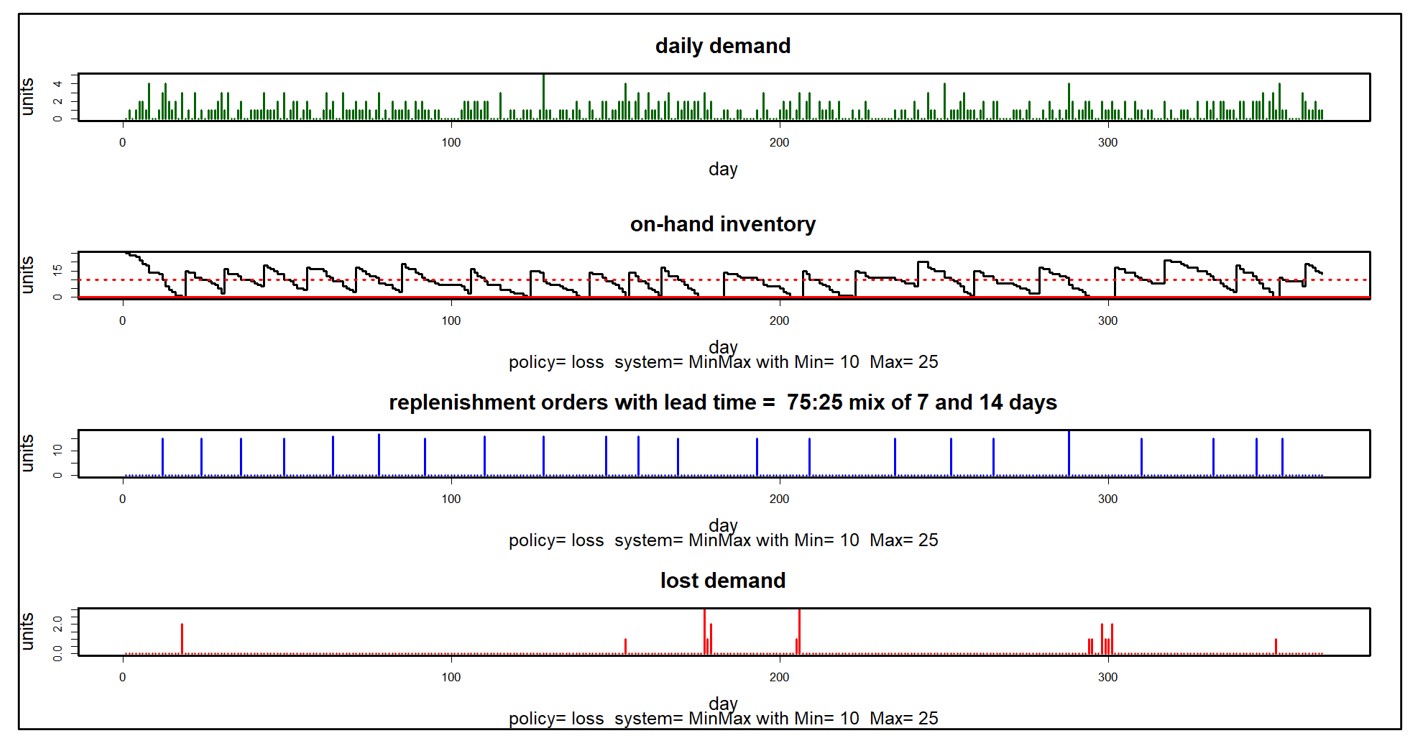
La figura 2 muestra parte del funcionamiento interno de una simulación de Monte Carlo de un sistema de inventario en cuatro paneles. El sistema utiliza una política de control de inventario Min/Max con Min=10 y Max=25. No se permiten pedidos atrasados: tienes el bien o pierdes el negocio. Los plazos de entrega del reabastecimiento suelen ser de 7 días, pero a veces de 14. Esta simulación duró un año.
El primer panel muestra un escenario complejo de demanda aleatoria en el que no hay demanda los fines de semana, pero la demanda generalmente aumenta cada día de lunes a viernes. El segundo panel muestra el número aleatorio de unidades disponibles, que sube y baja con cada ciclo de reabastecimiento. El tercer panel muestra los tamaños aleatorios y los tiempos de los pedidos de reposición que llegan del proveedor. El panel final muestra la demanda insatisfecha que pone en peligro las relaciones con los clientes. Este tipo de detalle puede ser muy útil para comprender mejor la dinámica de un sistema de inventario.
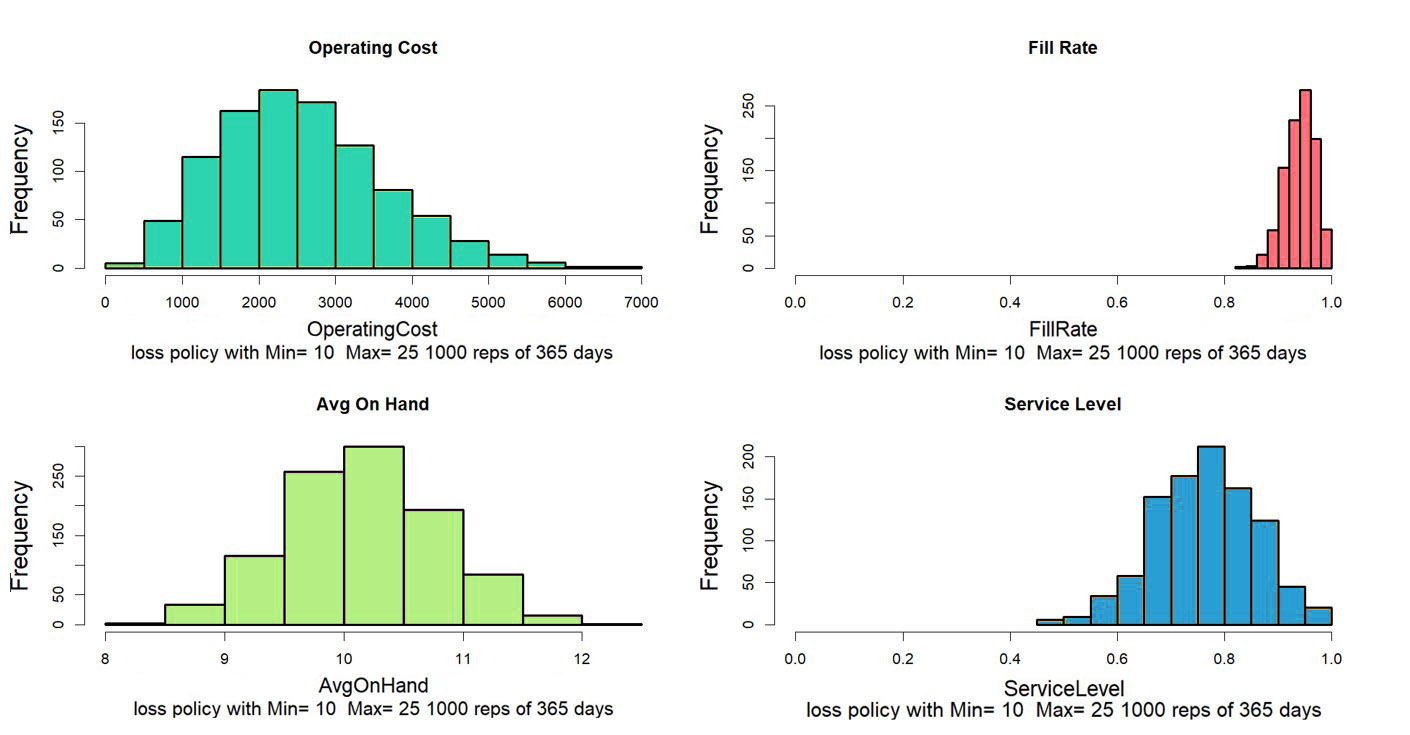
La Figura 2 muestra solo una de las innumerables formas en que podría desarrollarse el año. Generalmente, queremos promediar los resultados de muchos años simulados. Después de todo, nadie lanzaría una moneda al aire una vez para decidir si era una moneda justa. La Figura 3 muestra cómo cuatro métricas de rendimiento clave (KPI) varían de un año a otro para este sistema. Algunas métricas son relativamente estables en todas las simulaciones (tasa de llenado), pero otras muestran una variabilidad más relativa (costo operativo = costo de mantenimiento + costo de pedido + costo de escasez). Observando los gráficos, podemos estimar que las opciones de Min=10, Max=25 conducen a un costo operativo promedio de alrededor de $3,000 por año, una tasa de llenado de alrededor de 90%, un nivel de servicio de alrededor de 75% y un promedio de encendido. mano de unos 10
De hecho, ahora es posible responder a una pregunta de gestión de mayor nivel. Podemos ir más allá de "¿Qué pasará si hago tal y tal cosa?" a “¿Cuál es el mejor ¿Qué puedo hacer para lograr una tasa de relleno de al menos 90% para este artículo al costo más bajo posible? El matemágica detrás de este salto hay otra tecnología clave llamada "optimización estocástica", pero nos detendremos aquí por ahora. Baste decir que el software SIO&P de Smart puede buscar en el "espacio de diseño" de los valores mínimo y máximo para encontrar automáticamente la mejor opción.