Het beheren van de inventaris in een enkele faciliteit is al moeilijk genoeg, maar het probleem wordt veel complexer wanneer er meerdere faciliteiten zijn die in meerdere echelons zijn gerangschikt. De complexiteit komt voort uit de interacties tussen de echelons, waarbij de eisen op de lagere niveaus opborrelen en eventuele tekorten op de hogere niveaus die naar beneden stromen.
Als elk van de faciliteiten afzonderlijk zou worden beheerd, zouden standaardmethoden kunnen worden gebruikt, zonder rekening te houden met interacties, om parameters voor voorraadbeheer in te stellen, zoals bestelpunten en bestelhoeveelheden. Het negeren van de interacties tussen niveaus kan echter leiden tot catastrofale storingen. Ervaring en vallen en opstaan maken het ontwerpen van stabiele systemen mogelijk, maar die stabiliteit kan worden verstoord door veranderingen in vraagpatronen of doorlooptijden of door toevoeging van nieuwe faciliteiten. Het omgaan met dergelijke veranderingen wordt enorm geholpen door geavanceerde supply chain-analyses, die een veilige "sandbox" bieden waarin voorgestelde systeemwijzigingen kunnen worden getest voordat ze worden geïmplementeerd. Deze blog illustreert dat punt.
Het scenario
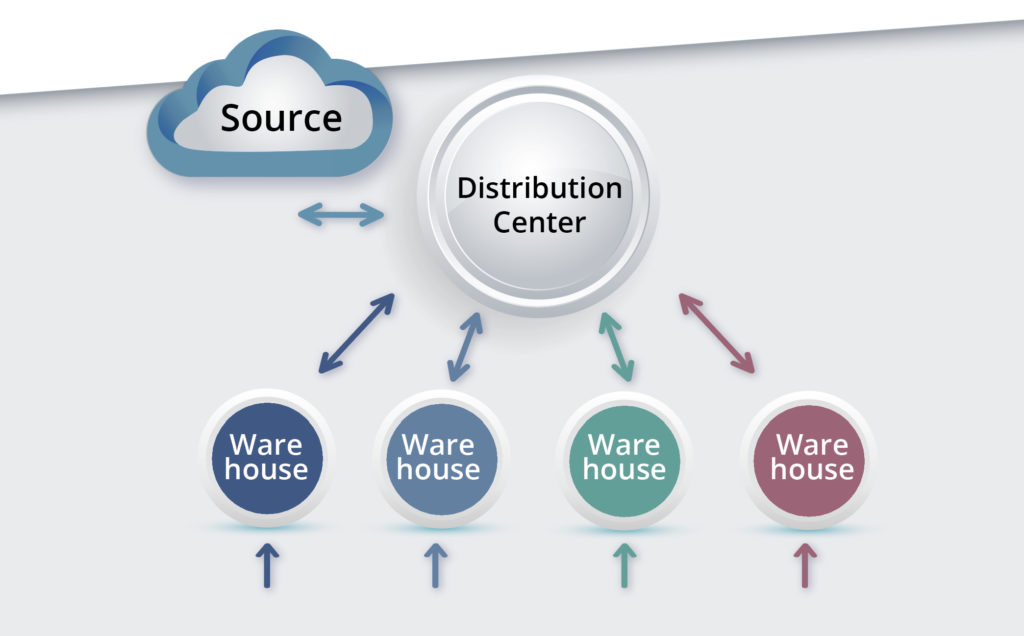
Om enige hoop te hebben dit probleem op een nuttige manier te bespreken, zal deze blog het probleem vereenvoudigen door de hiërarchie op twee niveaus te beschouwen die is afgebeeld in figuur 1. Stel u voor dat de faciliteiten op het lagere niveau magazijnen (WH's) zijn van waaruit moet worden voldaan aan de eisen van de klant , en dat de inventarisitems bij elke WH serviceonderdelen zijn die aan een breed scala aan externe klanten worden verkocht.
Figuur 1: Algemene structuur van één type voorraadsysteem op twee niveaus
Stel je voor dat het hogere niveau zou bestaan uit één distributiecentrum (DC) dat klanten niet rechtstreeks bedient, maar wel de WH's aanvult. Neem voor de eenvoud aan dat het DC zelf wordt aangevuld vanuit een Bron die altijd voldoende voorraad heeft (of maakt) om onderdelen onmiddellijk naar het DC te verzenden, zij het met enige vertraging. (Als alternatief zouden we het systeem kunnen overwegen om winkels door één magazijn te laten bevoorraden).
Elk niveau kan worden beschreven in termen van vraagniveaus (behandeld als willekeurig), doorlooptijden (willekeurig), voorraadbeheerparameters (hier, Min- en Max-waarden) en tekortbeleid (hier, naleveringen toegestaan).
De analysemethode
De academische literatuur heeft vooruitgang geboekt met betrekking tot dit probleem, hoewel dit meestal ten koste gaat van vereenvoudigingen die nodig zijn om een zuiver wiskundige oplossing mogelijk te maken. Onze aanpak is hier toegankelijker en flexibeler: Monte Carlo simulatie. Dat wil zeggen, we bouwen een computerprogramma dat de logica van de systeemwerking bevat. Het programma "creëert" willekeurige vraag op WH-niveau, verwerkt de vraag volgens de logica van een gekozen voorraadbeleid en creëert vraag naar het DC door de willekeurige verzoeken om aanvulling van de WH's te bundelen. Met deze benadering kunnen we veel gesimuleerde dagen van systeemwerking observeren terwijl we letten op belangrijke gebeurtenissen zoals stockouts op beide niveaus.
Een voorbeeld
Om een analyse te illustreren, hebben we een systeem gesimuleerd dat bestaat uit vier WH's en één DC. De gemiddelde vraag varieerde over de WH's. Aanvulling van het DC naar een WH duurde 4 tot 7 dagen, gemiddeld 5,15 dagen. Het aanvullen van de DC van de Bron duurde 7, 14, 21 of 28 dagen, maar 90% van de tijd was ofwel 21 of 28 dagen, wat neerkomt op een gemiddelde van 21 dagen. Elke faciliteit had Min- en Max-waarden die na enkele ruwe berekeningen werden bepaald door het oordeel van analisten.
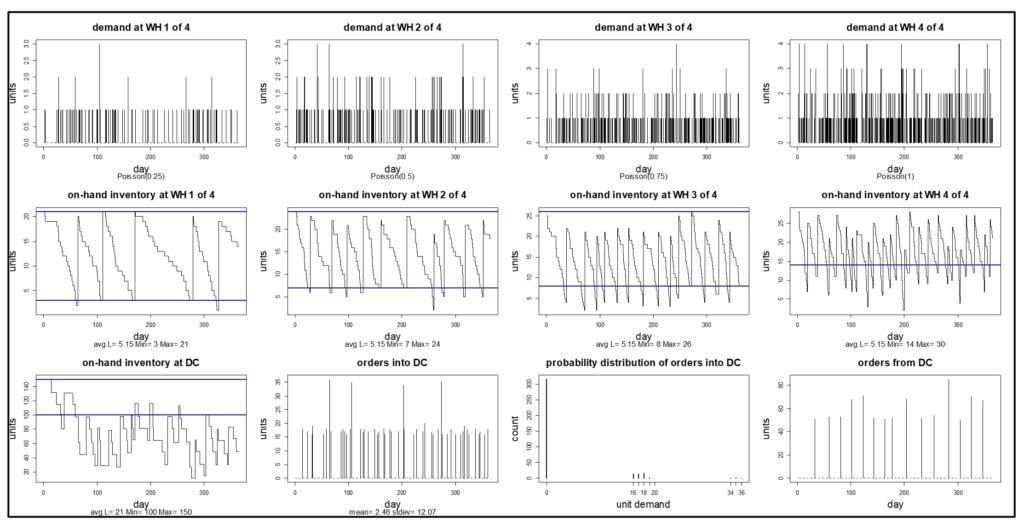
Figuur 2 toont de resultaten van een jaar gesimuleerde dagelijkse werking van dit systeem. De eerste rij in de figuur toont de dagelijkse vraag naar het item bij elke WH, waarvan werd aangenomen dat het "puur willekeurig" was, wat betekent dat het een Poisson-verdeling had. De tweede rij toont de voorhanden voorraad aan het einde van elke dag, met Min- en Max-waarden aangegeven door blauwe lijnen. De derde rij beschrijft de operaties op het DC. In tegenstelling tot de veronderstelling van veel theorieën, was de vraag naar het DC niet in de buurt van Poisson, en evenmin was de vraag vanuit het DC naar de Bron. In dit scenario waren de Min- en Max-waarden voldoende om ervoor te zorgen dat de artikelbeschikbaarheid hoog was bij elke WH en bij het DC, en er werden geen stockouts waargenomen bij een van de vijf faciliteiten.
Klik hier om de afbeelding te vergroten
Figuur 2 – Gesimuleerd gebruiksjaar van een systeem met vier WH's en één DC.
Laten we nu het scenario variëren. Wanneer stockouts uiterst zeldzaam zijn, zoals in figuur 2, is er vaak overtollige voorraad in het systeem. Stel dat iemand suggereert dat het voorraadniveau op het DC er een beetje dik uitziet en denkt dat het een goed idee zou zijn om daar geld te besparen. Hun suggestie om de voorraad op het DC te verminderen is om de waarde van de Min op het DC te verlagen van 100 naar 50. Wat gebeurt er? Je zou kunnen raden, of je zou kunnen simuleren.
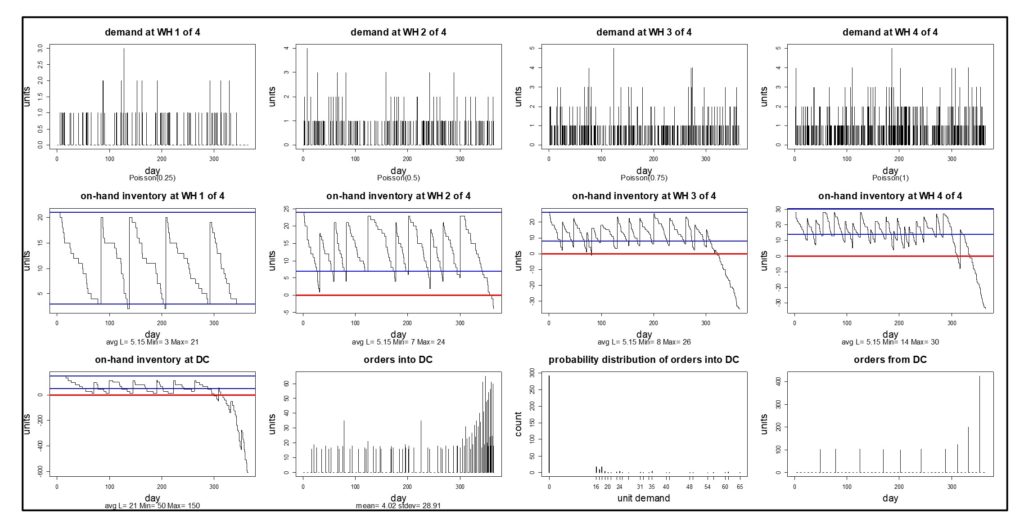
Figuur 3 toont de simulatie – het resultaat is niet mooi. Het systeem werkt een groot deel van het jaar prima, daarna raakt de voorraad van het DC op en kan het de achterstand niet meer inhalen ondanks het sturen van opeenvolgend grotere aanvullingsorders naar de bron. Drie van de vier WH's komen tegen het einde van het jaar in een doodsspiraal terecht (en WH1 volgt daarna). De simulatie heeft een gevoeligheid aan het licht gebracht die niet kan worden genegeerd en heeft een slechte beslissing gemarkeerd.
Klik hier om de afbeelding te vergroten
Figuur 3 – Gesimuleerde effecten van het verlagen van de Min bij de DC.
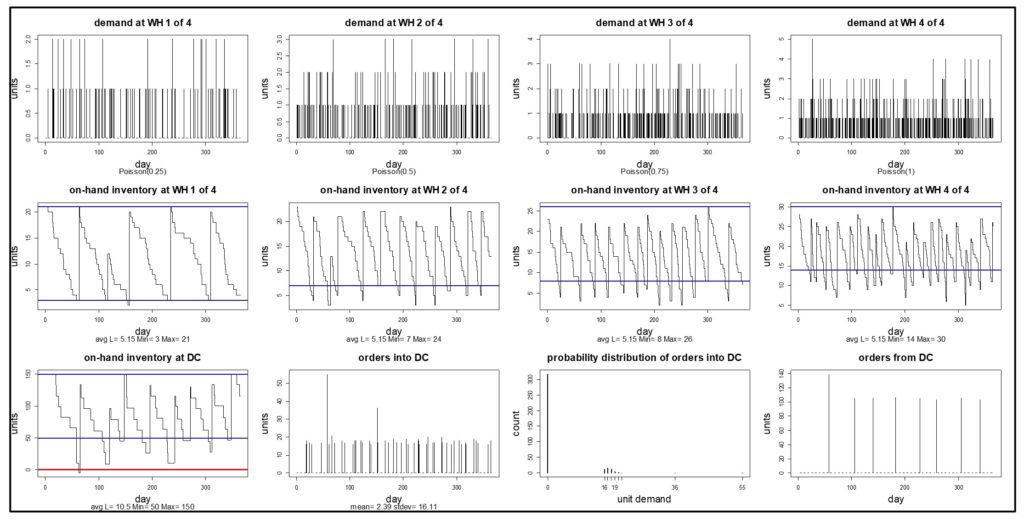
Nu kunnen de voorraadbeheerders terug naar de tekentafel en andere mogelijke manieren testen om de investering in voorraad op DC-niveau te verminderen. Een stap die altijd helpt, als u en uw leverancier dit samen kunnen realiseren, is om een flexibeler systeem te creëren door de doorlooptijd voor aanvullingen te verkorten. Door samen te werken met de bron om ervoor te zorgen dat het DC altijd binnen 7 of 14 dagen wordt aangevuld, wordt het systeem gestabiliseerd, zoals weergegeven in afbeelding 4.
Klik hier om de afbeelding te vergroten
Figuur 4 – Gesimuleerde effecten van het verkorten van de doorlooptijd voor het aanvullen van het DC.
Helaas is het voornemen om de voorraad op het DC te verminderen niet gehaald. De oorspronkelijke dagelijkse voorraadtelling was ongeveer 80 eenheden en blijft ongeveer 80 eenheden na verlaging van de DC's Min en drastische verbetering van de Source-to-DC doorlooptijd. Maar met het simulatiemodel kan het planningsteam andere ideeën uitproberen tot ze tot een bevredigend herontwerp komen. Of, aangezien figuur 4 laat zien dat de DC-voorraad met nul begint te flirten, zouden ze het misschien verstandig vinden om de behoefte aan gemiddeld ongeveer 80 eenheden in het DC te accepteren en in plaats daarvan te zoeken naar manieren om de voorraadinvesteringen bij de WH's te verminderen.
De afhaalrestaurants
- Multiechelon voorraadoptimalisatie (MEIO) is complex. Veel factoren werken samen om systeemgedrag te produceren dat zelfs in eenvoudige systemen met twee niveaus verrassend kan zijn.
- Monte Carlo-simulatie is een handig hulpmiddel voor planners die nieuwe systemen moeten ontwerpen of bestaande systemen moeten aanpassen.

Op prognoses gebaseerd voorraadbeheer voor een betere planning
Forecast-based inventory management, or MRP (Material Requirements Planning) logic, is a forward-planning method that helps businesses meet demand without overstocking or understocking. By anticipating demand and adjusting inventory levels, it maintains a balance between meeting customer needs and minimizing excess inventory costs. This approach optimizes operations, reduces waste, and enhances customer satisfaction.

Maak van AI-gestuurde voorraadoptimalisatie een bondgenoot voor uw organisatie
In deze blog onderzoeken we hoe organisaties uitzonderlijke efficiëntie en nauwkeurigheid kunnen bereiken met AI-gestuurde voorraadoptimalisatie. Traditionele methoden voor voorraadbeheer schieten vaak tekort vanwege hun reactieve karakter en hun afhankelijkheid van handmatige processen. Het handhaven van optimale voorraadniveaus is van fundamenteel belang om aan de vraag van de klant te voldoen en tegelijkertijd de kosten te minimaliseren. De introductie van AI-gestuurde voorraadoptimalisatie kan de last van handmatige processen aanzienlijk verminderen, waardoor supply chain-managers worden ontlast van vervelende taken.

Het belang van duidelijke definities van serviceniveaus bij voorraadbeheer
Voorraadoptimalisatiesoftware die 'wat als'-analyse ondersteunt, legt de afweging tussen voorraadtekorten en extra kosten van verschillende serviceniveaudoelen bloot. Maar eerst is het belangrijk om te identificeren hoe ‘serviceniveaus’ worden geïnterpreteerd, gemeten en gerapporteerd. Dit voorkomt miscommunicatie en het valse gevoel van veiligheid dat kan ontstaan als er minder strenge definities worden gebruikt. Als u duidelijk definieert hoe het serviceniveau wordt berekend, staan alle belanghebbenden op één lijn. Dit vergemakkelijkt een betere besluitvorming.