Voor de meeste kleine tot middelgrote fabrikanten en distributeurs is voorraadoptimalisatie op één niveau of op één echelon het allernieuwste in de logistieke praktijk. Multi-echelon voorraadoptimalisatie (“MEIO”) houdt in dat het spel op een nog hoger niveau wordt gespeeld en is daarom veel minder gebruikelijk. Deze blog is de eerste van twee. Het is bedoeld om uit te leggen wat MEIO is, waarom standaard MEIO-theorieën kapot gaan en hoe probabilistische modellering door scenariosimulatie de realiteit in het MEIO-proces kan herstellen. De tweede blog laat een specifiek voorbeeld zien.
Definitie van voorraadoptimalisatie
Een inventarisatiesysteem is gebaseerd op een reeks ontwerpkeuzes.
De eerste keuze is het beleid om te reageren op stockouts: verlies je gewoon de verkoop aan een concurrent, of kun je de klant overtuigen om een backorder te accepteren? Het eerste komt vaker voor bij distributeurs dan bij fabrikanten, maar dit is misschien niet zo'n goede keuze, omdat klanten het antwoord kunnen dicteren.
De tweede keuze is het voorraadbeleid. Deze zijn onderverdeeld in beleid voor "doorlopende beoordeling" en "periodieke beoordeling", met verschillende opties binnen elk type. U kunt een koppeling maken naar een videozelfstudie waarin verschillende algemene voorraadbeleidsregels worden beschreven hier. Misschien is de meest efficiënte bij beoefenaars bekend als "Min/Max" en bij academici als (s, S) of "kleine S, Grote S." We gebruiken dit beleid in onderstaande scenariosimulaties. Het werkt als volgt: Wanneer de voorhanden voorraad daalt tot of onder de Min (s), wordt een bestelling geplaatst voor aanvulling. De grootte van de bestelling is het gat tussen de voorhanden voorraad en de Max (S), dus als Min 10 is, Max 25 en voorhanden is 8, dan is het tijd voor een bestelling van 25-8 = 17 eenheden.
De derde keuze is om te beslissen over de beste waarden van de 'parameters' van het voorraadbeleid, bijv. de waarden die moeten worden gebruikt voor Min en Max. Voordat u getallen aan Min en Max toewijst, moet u duidelijkheid hebben over wat "beste" voor u betekent. Gewoonlijk betekent beste keuzes die de bedrijfskosten van de voorraad minimaliseren, afhankelijk van een minimum aan artikelbeschikbaarheid, uitgedrukt als Service Level of Fill Rate. In wiskundige termen is dit een "tweedimensionaal beperkt geheeltallig optimalisatieprobleem". "Tweedimensionaal" omdat je twee getallen moet kiezen: Min en Max. "Integer" omdat Min en Max hele getallen moeten zijn. "Beperkt" omdat u minimum- en maximumwaarden moet kiezen die een voldoende hoog niveau van artikelbeschikbaarheid bieden, zoals serviceniveaus en opvulpercentages. “Optimalisatie” omdat je daar wilt komen met de laagste operationele kosten (operationele kosten combineren kosten voor vasthouden, bestellen en tekorten).
Multiechelon-inventarisatiesystemen
Het optimalisatieprobleem wordt moeilijker in multi-echelonsystemen. In een systeem met één echelon kan elk voorraadartikel afzonderlijk worden geanalyseerd: één paar Min/Max-waarden per SKU. Omdat er meer onderdelen zijn in een multi-echelonsysteem, is er een groter rekenprobleem.
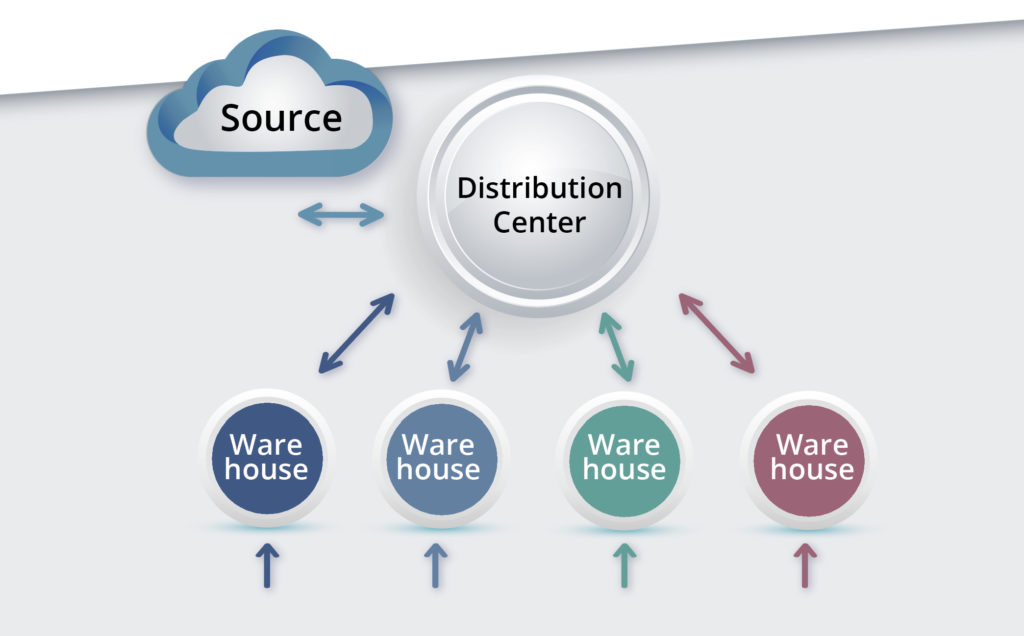
Afbeelding 1 toont een eenvoudig systeem met twee niveaus voor het beheren van een enkele SKU. Op het lagere niveau komen de vragen binnen bij meerdere magazijnen. Wanneer die dreigen op te raken, worden ze bevoorraad vanuit een distributiecentrum (DC). Wanneer de DC zelf dreigt vol te raken, wordt deze geleverd door een externe bron, zoals de fabrikant van het artikel.
Het ontwerpprobleem hier is multidimensionaal: we hebben Min- en Max-waarden nodig voor 4 magazijnen en voor het DC, dus de optimalisatie vindt plaats in 4×2+1×2=10 dimensies. De analyse moet rekening houden met een groot aantal contextuele factoren:
- Het gemiddelde niveau en de volatiliteit van de vraag die in elk magazijn binnenkomt.
- Het gemiddelde en de variabiliteit van de doorlooptijden van aanvullingen vanuit het DC.
- Het gemiddelde en de variabiliteit van de doorlooptijden voor aanvulling van de bron.
- Het vereiste minimale serviceniveau in de magazijnen.
- Het vereiste minimale serviceniveau op het DC.
- De voorraad-, bestel- en tekortkosten in elk magazijn.
- De bewaar-, bestel- en tekortkosten bij het DC.
Zoals je zou verwachten, zullen gissingen op de broekspijpen in deze situatie niet goed werken. Evenmin zal proberen het probleem te vereenvoudigen door elk echelon afzonderlijk te analyseren. Voorraden op het DC verhogen bijvoorbeeld het risico op stockouts op magazijnniveau en vice versa.
Dit probleem is duidelijk te ingewikkeld om te proberen op te lossen zonder hulp van een of ander computermodel.
Waarom standaard inventarisatietheorie slechte wiskunde is?
Met een beetje zoeken vind je modellen, tijdschriftartikelen en boeken over MEIO. Dit zijn waardevolle bronnen van informatie en inzicht, even getallen. Maar de meeste van hen vertrouwen op het hulpmiddel om het probleem te eenvoudig te maken om het schrijven en oplossen van vergelijkingen mogelijk te maken. Dit is de "Fantasie" waarnaar in de titel wordt verwezen.
Dit doen is een klassieke modelleringsmanoeuvre en is niet per se een slecht idee. Toen ik afstudeerde aan het MIT, leerde ik de waarde van het hebben van twee modellen: een klein, ruw model om als een soort vizier te dienen en een groter, nauwkeuriger model om betrouwbare getallen te produceren. Het kleinere model is gebaseerd op vergelijkingen en op theorie; het grotere model is gebaseerd op procedures en op gegevens, dwz een gedetailleerde systeemsimulatie. Modellen die gebaseerd zijn op eenvoudige theorieën en vergelijkingen kunnen slechte numerieke schattingen opleveren en zelfs hele verschijnselen over het hoofd zien. Daarentegen zullen modellen die gebaseerd zijn op procedures (bijv. "bestel tot de Max wanneer u de Min overschrijdt") en feiten (bijv. de laatste 3 jaar van de dagelijkse vraag naar artikelen) veel meer rekenkracht vergen, maar realistischere antwoorden geven. Gelukkig hebben we dankzij de cloud veel rekenkracht binnen handbereik.
Misschien wel de grootste modellering van "zonde" in de MEIO-literatuur is de veronderstelling dat eisen op alle echelons kunnen worden gemodelleerd als puur willekeurige Poisson-processen. Zelfs als het waar zou zijn op magazijnniveau, zou het verre van waar zijn op DC-niveau. Het Poisson-proces is de "witte rat van vraagmodellering" omdat het eenvoudig is en meer manipulatie van papier-en-potloodvergelijkingen mogelijk maakt. Omdat niet alle eisen Poisson-vormig zijn, resulteert dit in onrealistische aanbevelingen.
Op scenario's gebaseerde simulatie-optimalisatie
Om realisme te krijgen, moeten we dieper ingaan op de details van hoe de voorraadsystemen op elk echelon werken. Met weinig beperkingen, behalve die opgelegd door hardware, zoals de grootte van het geheugen, kunnen computerprogramma's elk niveau van complexiteit aan. Het is bijvoorbeeld niet nodig om aan te nemen dat elk van de magazijnen te maken heeft met identieke vraagstromen of dezelfde kosten heeft als alle andere.
Een computersimulatie werkt als volgt.
- De werkelijke vraaggeschiedenis en doorlooptijdgeschiedenis worden verzameld voor elke SKU op elke locatie.
- Waarden van voorraadparameters (bijv. Min en Max) worden geselecteerd voor proef.
- De vraag- en aanvullingsgeschiedenissen worden gebruikt om scenario's te creëren die de invoer naar het computerprogramma weergeven dat de werkingsregels van het systeem codeert.
- De ingangen worden gebruikt om de werking van een computermodel van het systeem aan te sturen met de gekozen parameterwaarden over een lange periode, bijvoorbeeld een jaar.
- Voor het gesimuleerde jaar worden key performance indicators (KPI's) berekend.
- Stappen 2-5 worden vele malen herhaald en de resultaten worden gemiddeld om parameterkeuzes te koppelen aan systeemprestaties.
Voorraadoptimalisatie voegt nog een "buitenste lus" toe aan de berekeningen door systematisch te zoeken naar de mogelijke waarden van Min en Max. Van de parameterparen die voldoen aan de artikelbeschikbaarheidsbeperking, identificeert verder zoeken de Min- en Max-waarden die resulteren in de laagste bedrijfskosten.
Figuur 1: Algemene structuur van één type voorraadsysteem op twee niveaus
Blijf op de hoogte voor onze volgende blog
BINNENKORT BESCHIKBAAR. Om een voorbeeld van een simulatie van het systeem in figuur 1 te zien, lees de tweede blog over dit onderwerp

Het beheren van de voorraad reserveonderdelen: beste praktijken
In this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs.

12 Oorzaken van Overstocking en Praktische Oplossingen
Effectief voorraadbeheer is cruciaal voor het behouden van een gezonde balans en het verzekeren dat middelen optimaal worden toegewezen. Hier is een diepgaande verkenning van de belangrijkste oorzaken van overstocking, hun implicaties en mogelijke oplossingen.

FAQ: Slimme IP&O voor beter voorraadbeheer.
Effective supply chain and inventory management are essential for achieving operational efficiency and customer satisfaction. This blog provides clear and concise answers to some basic and other common questions from our Smart IP&O customers, offering practical insights to overcome typical challenges and enhance your inventory management practices. Focusing on these key areas, we help you transform complex inventory issues into strategic, manageable actions that reduce costs and improve overall performance with Smart IP&O.