Verbeter de forecasting nauwkeurigheid, elimineer overtollige voorraad en maximaliseer service levels

In deze video-tutorial presenteert Dr. Thomas Willemain, mede-oprichter en SVP Research bij Smart Software, regressieanalyse, een gespecialiseerde statistische modelleringstechniek om leidende indicatoren te identificeren en te benutten om nauwkeurigere voorspellingen te bereiken. Regressieanalyse is een statistische procedure om de relatie tussen een responsvariabele en een of meer voorspellende variabelen te schatten. Het starten van woningen kan bijvoorbeeld een goede voorlopende indicator zijn van de vraag naar vinylbeplating. Tom legt uit hoe en wanneer je regressieanalyse gebruikt en werkt een praktijkvoorbeeld uit.

Degenen die prognoses maken, zijn het verschuldigd aan degenen die prognoses consumeren, en aan zichzelf, om zich bewust te zijn van de onzekerheid in hun prognoses. Deze notitie gaat over het schatten van prognoseonzekerheid en het gebruik van de schattingen in uw vraagplanningsproces. We richten ons op prognoses die zijn gemaakt ter ondersteuning van vraagplanning en op prognoses die inherent zijn aan voorraad optimaliseren beleid met betrekking tot bestelpunten, veiligheidsvoorraden en min/max-niveaus.

Als je dit leest, leer je over:

- Criteria voor het beoordelen van prognoses
-Bronnen van voorspellingsfout
- Berekening van de voorspellingsfout
-Voorspellingsfout omzetten in voorspellingsintervallen
-De relatie tussen vraagvoorspelling en voorraadoptimalisatie.
-Acties die u kunt ondernemen om deze concepten te gebruiken om de processen van uw bedrijf te verbeteren.

Criteria voor het beoordelen van prognoses

Voorspellingsfouten alleen zijn geen reden genoeg om prognoses als managementtool af te wijzen. Om een beroemd aforisme van George Box te verdraaien: "Alle voorspellingen zijn verkeerd, maar sommige zijn nuttig." Natuurlijk zullen zakelijke professionals altijd zoeken naar manieren om prognoses nuttiger te maken. Dit omvat meestal werk om prognosefouten te verminderen. Maar hoewel de nauwkeurigheid van prognoses het meest voor de hand liggende criterium is om prognoses te beoordelen, is het niet het enige. Hier is een lijst met criteria voor het evalueren van prognoses:

Nauwkeurigheid: Voorspellingen van toekomstige waarden zouden, achteraf bezien, heel dicht bij de werkelijke waarden moeten liggen die zich uiteindelijk zullen openbaren. Maar er kan een afnemend rendement zijn om nog een half procent nauwkeurigheid uit prognoses te persen die anders goed genoeg zijn om te gebruiken bij het nemen van beslissingen.

Tijdigheid: Gevechtspiloten verwijzen naar de OODA-lus (observeren, oriënteren, beslissen en handelen) en de "noodzaak om in de OODA-lus van de vijand te komen" zodat ze als eerste kunnen schieten. Ook bedrijven hebben beslissingscycli. Het leveren van een perfect nauwkeurige voorspelling de dag nadat het nodig was, is niet nuttig. Beter is een goede voorspelling die op tijd aankomt om bruikbaar te zijn.

Kosten: Het voorspellen van data, modellen, processen en mensen kosten allemaal geld. Een goedkopere prognose kan worden gevoed door gegevens die direct beschikbaar zijn; duurder zou een prognose zijn die draait op gegevens die moeten worden verzameld in een speciaal proces buiten de reikwijdte van de informatie-infrastructuur van een bedrijf. Een klassieke, kant-en-klare prognosetechniek zal minder duur zijn om aan te schaffen, te voeden en te exploiteren dan een complexe, op maat gemaakte, door een adviseur geleverde methode. Prognoses kunnen massaal worden geproduceerd door software onder supervisie van een enkele analist, of ze kunnen voortkomen uit een samenwerkingsproces dat tijd en inspanning vereist van grote groepen mensen, zoals districtsverkoopmanagers, productieteams en anderen. Technisch geavanceerde voorspellingstechnieken vereisen vaak het inhuren van personeel met gespecialiseerde technische expertise, zoals een masterdiploma in statistiek, dat doorgaans meer kost dan personeel met een minder geavanceerde opleiding.

Geloofwaardigheid: Uiteindelijk moet een leidinggevende elke prognose accepteren en ernaar handelen. Leidinggevenden hebben de neiging aanbevelingen te wantrouwen of te negeren die ze niet kunnen begrijpen of uitleggen aan de volgende persoon boven hen in de hiërarchie. Voor velen is geloven in een "zwarte doos" een te zware geloofsbeproeving, en zij verwerpen de voorspellingen van de zwarte doos ten gunste van iets transparanters.

Dat gezegd hebbende, zullen we ons nu concentreren op de voorspellingsnauwkeurigheid en de kwaadaardige tweeling, voorspellingsfout.

Bronnen van prognosefouten

Degenen die fouten willen verminderen, kunnen op drie plaatsen zoeken naar problemen:
1. De gegevens die in een prognosemodel gaan
2. Het model zelf
3. De context van de prognoseoefening

Er zijn verschillende manieren waarop gegevensproblemen kunnen leiden tot prognosefouten.

Grove fouten: Verkeerde data leveren verkeerde voorspellingen op. We hebben een geval gezien waarin computergegevens van de vraag naar producten een factor twee verkeerd waren! De betrokkenen zagen dat probleem meteen, maar een minder ernstige situatie kan er gemakkelijk doorheen glippen om het prognoseproces te vergiftigen. Sterker nog, het organiseren, verwerven en controleren van data is vaak de grootste bron van vertraging bij de implementatie van forecasting software. Veel gegevensproblemen lijken voort te komen uit het feit dat de gegevens onbelangrijk waren totdat een prognoseproject ze belangrijk maakte.

Afwijkingen: Zelfs met perfect samengestelde prognosedatabases, zijn er vaak gegevensproblemen van het type "naald in een hooiberg". In deze gevallen zijn het niet de gegevensfouten, maar vraagafwijkingen die bijdragen aan de voorspellingsfout. In een set van bijvoorbeeld 50.000 producten is het waarschijnlijk dat een bepaald aantal artikelen vreemde details heeft die prognoses kunnen vertekenen.

Holdout-analyse is een eenvoudige maar krachtige analysemethode. Om te zien hoe goed een methode voorspelt, gebruikt u deze met oudere bekende gegevens om nieuwere gegevens te voorspellen en ziet u vervolgens hoe het zou zijn uitgekomen! Stel dat u 36 maanden aan vraaggegevens heeft en 3 maanden vooruit moet voorspellen. U kunt het prognoseproces simuleren door de meest recente 3 maanden aan gegevens achter te houden (dwz te verbergen), prognoses te maken met alleen gegevens van maand 1 tot 33 en vervolgens de prognoses voor maanden 34-36 te vergelijken met de werkelijke waarden in maanden 34-36 . Glijdende simulatie herhaalt alleen de holdout-analyse en glijdt langs de vraaggeschiedenis. In het bovenstaande voorbeeld werden de gegevens van de eerste 33 maanden gebruikt om 3 schattingen van de voorspellingsfout te krijgen. Stel dat we het proces starten door de eerste 12 maanden te gebruiken om de volgende 3 te voorspellen. Dan schuiven we vooruit en gebruiken de eerste 13 maanden om de volgende 3 te voorspellen. We gaan door totdat we uiteindelijk de eerste 35 maanden gebruiken om de laatste maand te voorspellen, wat geeft ons nog een schatting van de fout die we maken bij het voorspellen van een maand vooruit. Een samenvatting van alle 1-stap vooruit, 2-stap vooruit en 3 stap vooruit voorspellingsfouten biedt een manier om voorspellingsintervallen te berekenen.

Voorspellingsintervallen berekenen

De laatste stap bij het berekenen van voorspellingsintervallen is het omzetten van de schattingen van de gemiddelde absolute fout in de boven- en ondergrenzen van het voorspellingsinterval. Het voorspellingsinterval op een willekeurig tijdstip in de toekomst wordt berekend als

Voorspellingsinterval = Voorspelling ± Vermenigvuldiger x Gemiddelde absolute fout.

De laatste stap is de keuze van de vermenigvuldiger. De typische benadering is om een kansverdeling van fouten rond de voorspelling voor te stellen en vervolgens de uiteinden van het voorspellingsinterval te schatten met behulp van de juiste percentielen van die verdeling. Gewoonlijk is de veronderstelde foutverdeling de normale verdeling, ook wel de Gaussische verdeling of de "klokvormige curve" genoemd.

Gebruik van voorspellingsintervallen
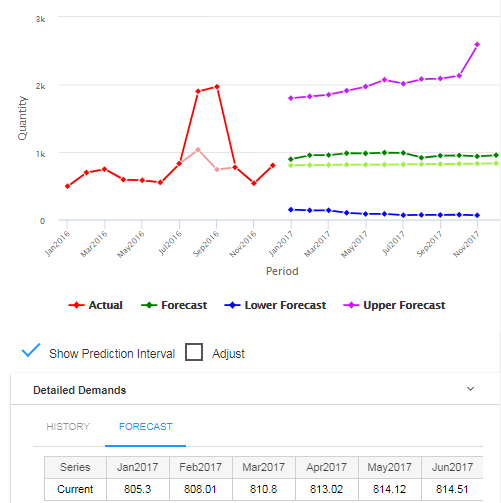
Het meest directe, informele gebruik van voorspellingsintervallen is om een idee te geven van hoe "squishy" een voorspelling is. Voorspellingsintervallen die breed zijn in vergelijking met de omvang van de prognoses wijzen op een grote onzekerheid.

Er zijn twee meer formele toepassingen bij vraagprognoses: het afdekken van uw weddenschappen over de toekomstige vraag en het begeleiden van prognoseaanpassingen.

Uw weddenschappen afdekken: De prognosewaarden zelf benaderen de meest waarschijnlijke waarden van de toekomstige vraag. Een meer onheilspellende manier om hetzelfde te zeggen is dat er een kans van ongeveer 50% is dat de werkelijke waarde boven (of onder) de voorspelling zal liggen. Als de prognose wordt gebruikt om toekomstige productie te plannen (of de aankoop of aanwerving van grondstoffen), wilt u misschien een buffer inbouwen om te voorkomen dat u tekort komt als de vraag piekt (ervan uitgaande dat onderbouw erger is dan overbouw). Als de prognose wordt geconverteerd van eenheden naar dollars voor omzetprognoses, wilt u misschien een waarde onder de prognose gebruiken om conservatief te zijn bij het projecteren van de cashflow. In beide gevallen moet u eerst de dekking van het voorspellingsinterval kiezen. Een 90%-voorspellingsinterval is een bereik van waarden dat 90% van de mogelijkheden dekt. Dit impliceert dat er een kans van 5% is dat een waarde boven de bovengrens van het 90%-voorspellingsinterval valt. Met andere woorden, de bovengrens van een 90%-voorspellingsinterval markeert het 95e percentiel van de verdeling van de voorspelde vraag in die periode. Evenzo is er een kans van 5% om onder de ondergrens te vallen, wat het 5e percentiel van de vraagverdeling markeert.

Begeleidende voorspellingsaanpassing: Het komt vrij vaak voor dat statistische prognoses worden herzien door een of ander samenwerkingsproces. Deze aanpassingen zijn gebaseerd op informatie die niet is vastgelegd in de vraaggeschiedenis van een item, zoals informatie over acties van concurrenten. Soms zijn ze gebaseerd op een meer vluchtige bron, zoals het optimisme van het verkoopteam. Wanneer de aanpassingen op het scherm worden aangebracht zodat iedereen ze kan zien, bieden de voorspellingsintervallen een nuttige referentie: als iemand de voorspellingen buiten de voorspellingsintervallen wil verplaatsen, overschrijden ze een op feiten gebaseerde grens en moeten ze een goed verhaal hebben om hun argument dat de dingen in de toekomst echt anders zullen zijn.

Voorspellingsintervallen en voorraadoptimalisatie

Ten slotte speelt het concept achter voorspellingsintervallen een essentiële rol in een probleem met betrekking tot vraagvoorspelling: Voorraad optimalisatie.
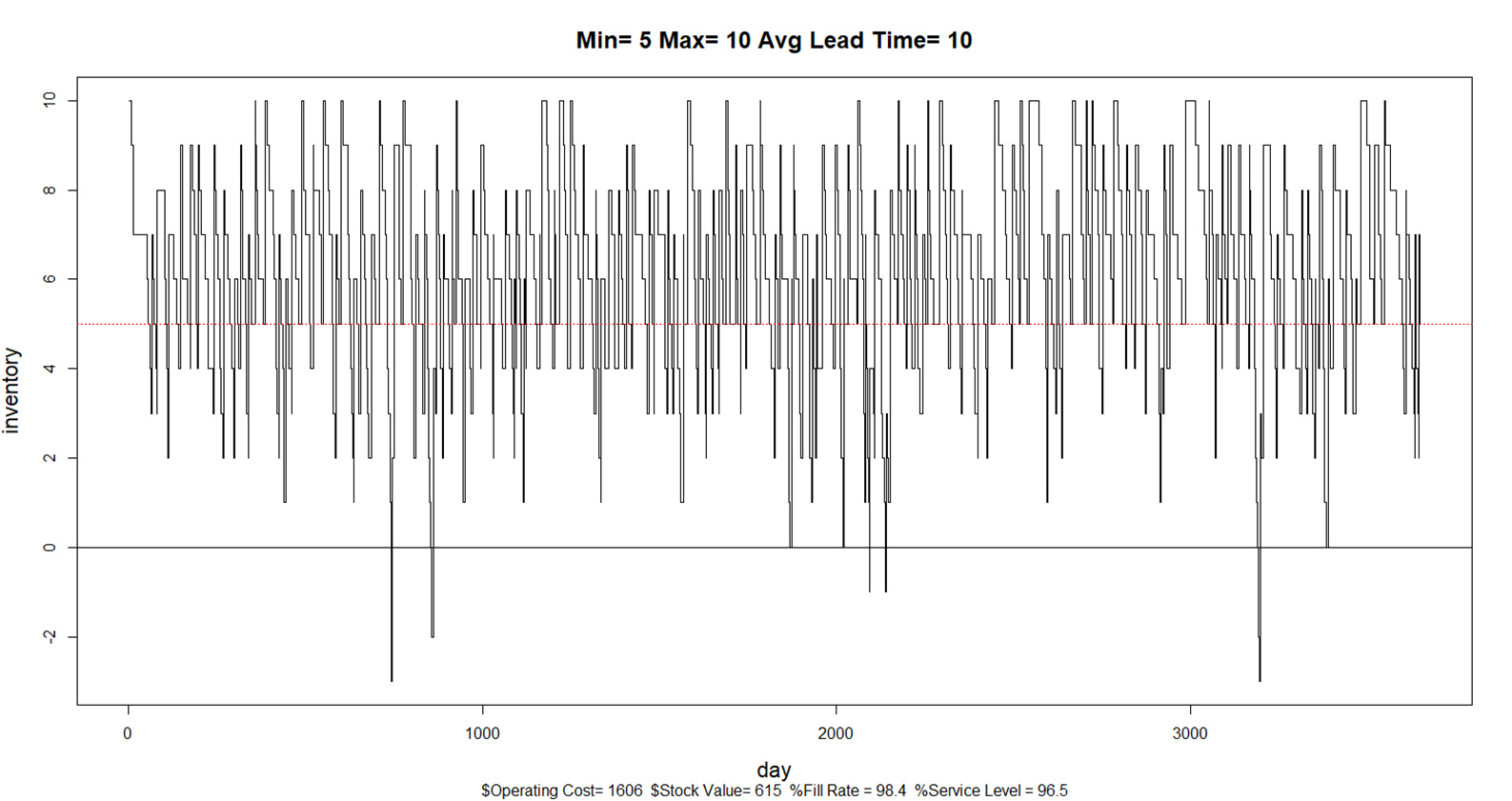
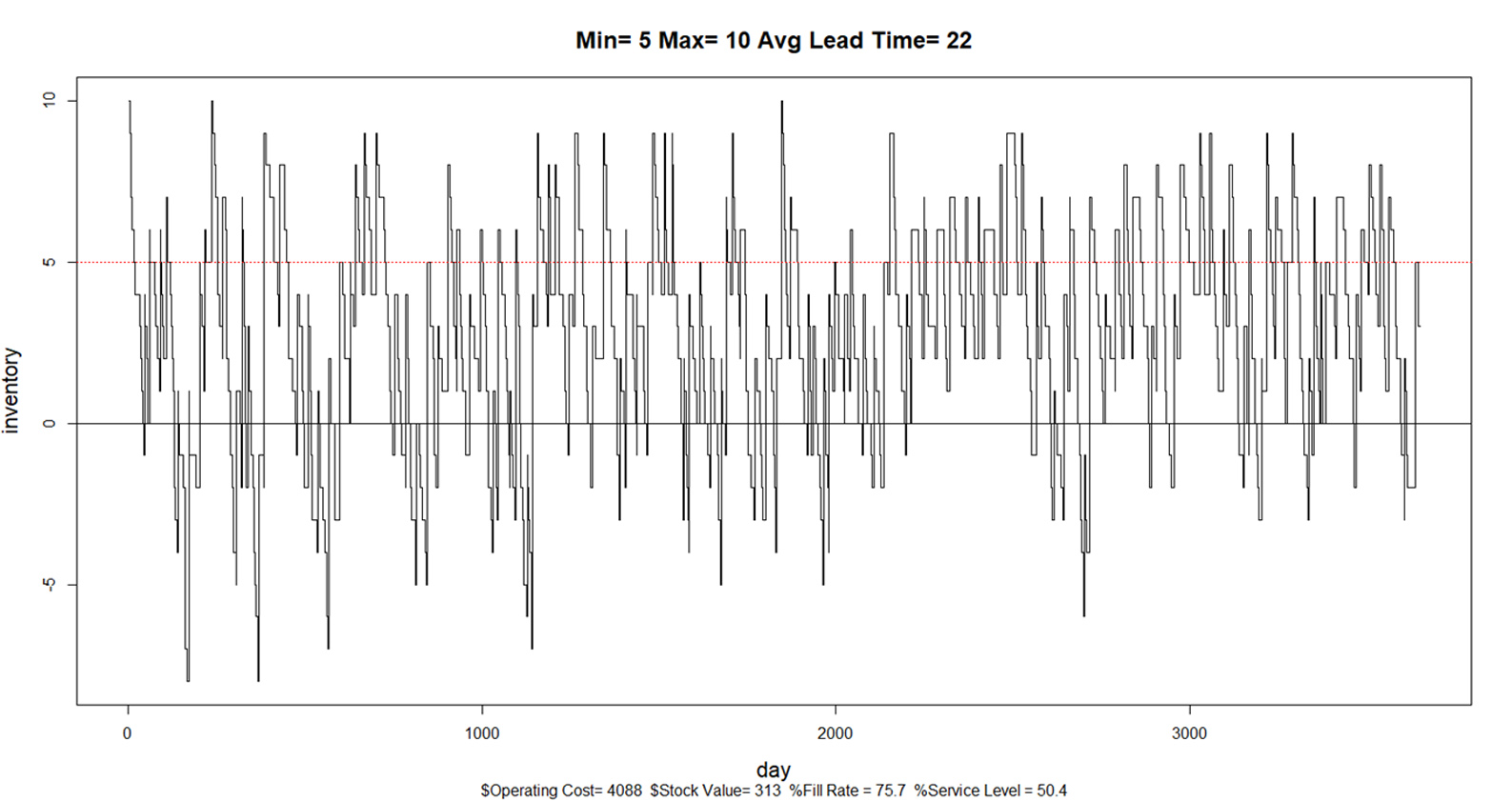
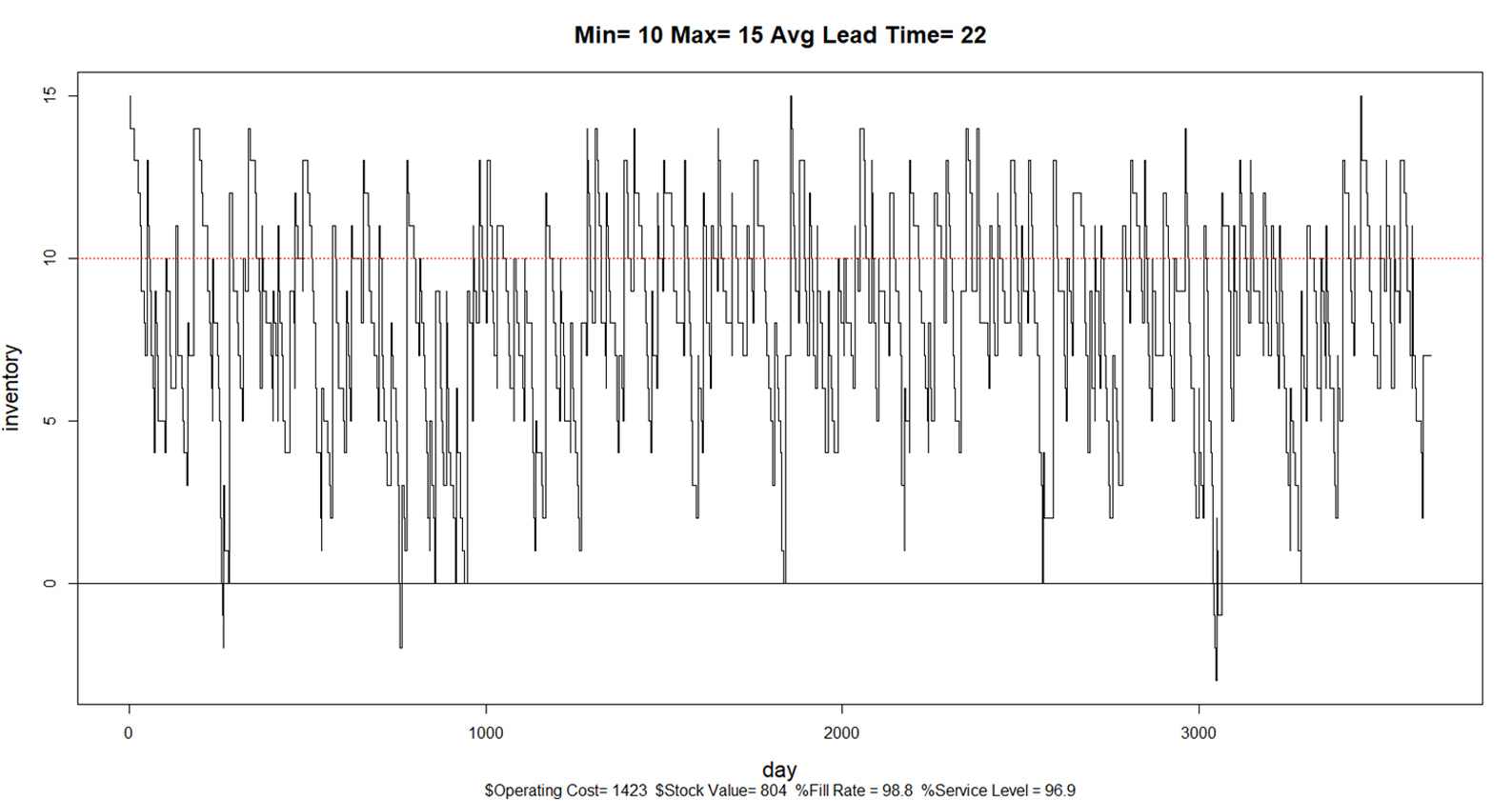
De belangrijkste analytische taak bij het instellen van bestelpunten (ook wel Mins genoemd) is het voorspellen van de totale vraag over een doorlooptijd voor aanvulling. Dit totaal wordt de doorlooptijdvraag genoemd. Wanneer de voorhanden voorraad daalt tot of onder het bestelpunt, wordt een aanvullingsorder geactiveerd. Als het bestelpunt hoog genoeg is, is er een acceptabel klein risico op voorraaduitval, dat wil zeggen dat de doorlooptijdvraag de voorraad onder nul brengt en leidt tot verloren verkopen of nabestellingen.

Nieuwe statistische methoden, en we kunnen effectiever gaan plannen.

De prognosetaak is het bepalen van alle mogelijke waarden van de cumulatieve vraag over de doorlooptijd en hun bijbehorende kansen van optreden. Met andere woorden, de basistaak is het bepalen van een voorspellingsinterval voor een toekomstige willekeurige variabele. Stel dat u een 90%-voorspellingsinterval hebt berekend voor de doorlooptijdvraag. Dan vertegenwoordigt de bovenkant van het interval het 95e percentiel van de verdeling. Door het bestelpunt op dit niveau in te stellen, is er plaats voor 95% van de mogelijke vraagwaarden voor de doorlooptijd, wat betekent dat er slechts een kans van 5% is dat de voorraad is uitgeput voordat de voorraad wordt aangevuld om de schappen opnieuw te bevoorraden. Er is dus een nauw verband tussen voorspellingsintervallen bij vraagprognoses en de berekening van bestelpunten bij voorraadoptimalisatie.

5 aanbevelingen voor de praktijk

1. Stel verwachtingen over fouten: Soms hebben managers onredelijke verwachtingen over het terugbrengen van prognosefouten tot nul. U kunt erop wijzen dat fouten slechts één van de dimensies is waarop een prognoseproces moet worden beoordeeld; het kan goed gaan met zowel tijdigheid als kosten. Wijs er ook op dat nul fouten evenmin een realistischer doel is dan 100% conversie van prospects naar klanten, perfecte leveranciersprestaties of nul volatiliteit van aandelenkoersen.

2. Spoor bronnen van fouten op: controleer de nauwkeurigheid van vraaggeschiedenissen. Gebruik statistische methoden om uitschieters in vraaggeschiedenissen te identificeren en gepast te reageren, geverifieerde anomalieën te vervangen door meer typische waarden en gegevens weg te laten van vóór grote veranderingen in de aard van de vraag. Als u een gezamenlijk prognoseproces gebruikt, vergelijkt u de nauwkeurigheid ervan met een puur statistische benadering om items te identificeren waarvoor samenwerking de fouten niet vermindert.

3. Evalueer de fout van alternatieve statistische methoden: er kunnen kant-en-klare technieken zijn die het beter doen dan uw huidige methoden, of het beter doen voor sommige subsets van uw items. De sleutel is om empirisch te zijn, gebruikmakend van het idee van holdout-analyse. Verzamel uw gegevens en doe een "bake off" tussen verschillende methoden om te zien welke voor u beter werken. Als u nog geen statistische prognosemethoden gebruikt, vergelijk ze dan met de "gouden buik" van uw huidige standaard. Gebruik de naïeve voorspelling als maatstaf in de vergelijkingen.

4. Onderzoek het gebruik van nieuwe gegevensbronnen: Vooral als u items heeft die veel gepromoot worden, test u statistische methoden die promotionele gegevens opnemen in het prognoseproces. Ga ook na of er misbruik kan worden gemaakt van informatie van buiten uw bedrijf; kijk bijvoorbeeld of macro-economische indicatoren voor uw sector kunnen worden gecombineerd met bedrijfsgegevens om de nauwkeurigheid van prognoses te verbeteren (dit wordt meestal gedaan met behulp van een methode die meervoudige regressieanalyse wordt genoemd).

5. Gebruik voorspellingsintervallen: Plots van voorspellingsintervallen kunnen uw gevoel voor de onzekerheid in uw prognoses verbeteren, waardoor u items kunt selecteren voor extra onderzoek. Hoewel het waar is dat wat je niet weet je pijn kan doen, is het ook waar dat weten wat je niet weet je kan helpen.

Verbeter de forecasting nauwkeurigheid, elimineer overtollige voorraad en maximaliseer service levels

In deze video definieert en vergelijkt Dr. Thomas Willemain, mede-oprichter en SVP Research, de meest bruikbare voorspellingstechnieken: Exponential Smoothing, Single Exponential Smoothing, Holt's Method en Winter's Method. Deze video's leggen het basisdenken onder elke techniek uit, evenals de wiskunde erachter, hoe ze in de praktijk worden gebruikt en de wisselwerking van elke methode.

Beleid en strategieën voor voorraadbeheer voor een winstgevender bedrijf

In deze video definieert en vergelijkt Dr. Thomas Willemain, mede-oprichter en SVP Research, de drie meest gebruikte beleidsregels voor voorraadbeheer. Dit beleid is onderverdeeld in twee groepen, periodieke beoordeling en doorlopende beoordeling. Er is ook een vierde beleid genaamd MRP-logica of op prognoses gebaseerde voorraadplanning dat is het onderwerp van een aparte videoblog die je hier kunt zien. Deze video's leggen elke polis uit, hoe ze in de praktijk worden gebruikt en de voor- en nadelen van elke aanpak.

​Terwijl de wereld zijn adem inhoudt om te zien hoe het nieuwe coronavirus (2019-nCOV) zich zal ontwikkelen, kruisen we onze vingers voor al diegenen die momenteel in quarantaine of onder behandeling zijn en bidden dat gezondheidsautoriteiten over de hele wereld binnenkort de overhand zullen krijgen .

Deze korte opmerking gaat over een manier waarop uw bedrijf een plan kan ontwikkelen om zich aan te passen aan een van de mogelijke gevolgen van het virus: plotselinge toename van de tijd die nodig is om voorraadaanvulling van leveranciers te krijgen. Toeleveringsketens over de hele wereld worden verstoord. Als dit jou overkomt, hoe kun je dan systematisch reageren?

Reageren op langere doorlooptijden

Dit is een probleem dat kan worden opgelost met behulp van geavanceerde supply chain-analyses. Waarschijnlijk hebt u deze technologie al gebruikt om goede keuzes te maken voor de controleparameters die worden gebruikt bij het beheer van al uw voorraaditems, bijvoorbeeld waarden voor Min en Max of bestelpunt en bestelhoeveelheid. De specifieke technische vraag die hier aan de orde komt, is hoe een toename van de doorlooptijd van aanvullingen kan worden omgezet in veranderingen in die controleparameters.

Over het algemeen vereisen langere doorlooptijden dikkere voorraden als u een hoog niveau van klantenservice wilt behouden. Deze algemene regel vertaalt zich in grotere waarden van Min en/of Max. Hoeveel groter hangt kritisch af van welke nieuwe, langere doorlooptijdwaarden zullen verschijnen en hun waarschijnlijkheid van voorkomen.

Hoewel veel planningssoftwaresystemen uitgaan van een vaste doorlooptijd, is de realiteit dat bijna alle doorlooptijden een zekere mate van willekeur hebben. Door te negeren dat willekeur het risico op stockout vergroot, is het belangrijk om een goede schatting te hebben van de waarschijnlijkheidsverdeling van doorlooptijden. In normale tijden kunnen uw transactiegegevens worden gebruikt om die relatie in te schatten. Maar plotselinge verstoringen zoals 2019-nCOV creëren ongekende situaties waarin u weloverwogen moet raden welke nieuwe vertragingen u zult zien en hoe waarschijnlijk die zijn. We gaan er hier van uit dat u zich een aantal van dergelijke scenario's kunt voorstellen en wilt uitzoeken hoe u er het beste op kunt reageren.

Een voorbeeld met behulp van geavanceerde software

Overweeg een hypothetisch voorbeeld om dit soort prospectieve planning te illustreren. Eén item, een reserveonderdeel, heeft een vast patroon van doorlooptijden voor aanvulling, met vertragingen van 5, 10 en 15 dagen met respectievelijk 15%-, 70%- en 15%-kansen. Gezien deze verdeling en een willekeurige vraag van gemiddeld één eenheid per 5 dagen, doen waarden van Min = 5 en Max = 10 het goed. Figuur 1 toont een simulatie van 10 jaar dagelijks gebruik onder dit scenario. Het opvullingspercentage en het serviceniveau zijn hoog, en stockouts komen niet vaak voor.

Stel nu dat verstoringen in de supply chain zorgen voor een minder gunstige verdeling van de doorlooptijd, met een 50:50 mix van 15 en 30 dagen. Figuur 2 laat zien hoe slecht de huidige waarden van Min en Max presteren in dit nieuwe scenario. Het vulpercentage en het serviceniveau kelderen als gevolg van frequente stockouts. Bedrijfskosten meer dan verdrievoudigd door boetes voor backorders. Alleen voorraadinvesteringen (de gemiddelde dollarwaarde van de voorraad in het schap) lijken beter te worden, maar dit gebeurt alleen omdat er zo vaak backorders zijn met niets meer op het schap. De verschuiving naar langere doorlooptijden vraagt duidelijk om nieuwe hogere waarden van Min en Max.

Afbeelding 3 laat zien hoe het systeem presteert wanneer de Min wordt verhoogd van 5 naar 10 en de Max van 10 naar 15. Deze wijziging compenseert de langere doorlooptijden en herstelt de eerdere hoge niveaus van opvullingspercentage en serviceniveau. Voorraadinvesteringen zijn noodzakelijkerwijs groter, maar de bedrijfskosten zijn in feite lager dan voorheen.

Overzicht

Veranderingen in de normale bedrijfsomstandigheden vereisen aanpassingen in de manier waarop voorraaditems worden beheerd. Een van die grote veranderingen die op deze datum opdoemt, is de potentiële impact van het 2019-nCOV Corona-virus op de toeleveringsketens, met verwachte langere bevoorradingstijden.

Wijzigingen in doorlooptijden vereisen wijzigingen in voorraadbeheerparameters zoals min's en max's. Deze wijzigingen zijn moeilijk met enig vertrouwen door te voeren met puur giswerk. Maar met enige inschatting van de toename van doorlooptijden, kunt u geavanceerde software gebruiken om met enig vertrouwen te leren hoe u deze aanpassingen kunt maken.

Deze notitie illustreert dit punt aan de hand van simulaties van de dagelijkse werking van een voorraadbeheersysteem.

Figuur 1 Simulatie van normale operaties met behulp van huidige bevoorradingsdoorlooptijden, Min en Max

Figuur 2 Simulatie van abnormale operaties met langere doorlooptijden en huidige Min en Max

Figuur 3 Simulatie van abnormale operaties met langere doorlooptijden en herziene Min en Max