En este blog, exploraremos cómo las organizaciones pueden lograr una eficiencia y precisión excepcionales con la optimización del inventario impulsada por la IA. Los métodos tradicionales de gestión de inventario a menudo resultan insuficientes debido a su naturaleza reactiva y su dependencia de procesos manuales. Mantener niveles óptimos de inventario es fundamental para satisfacer la demanda de los clientes y minimizar los costos. La introducción de la optimización del inventario impulsada por la IA puede reducir significativamente la carga de los procesos manuales, brindando alivio a los gerentes de la cadena de suministro de tareas tediosas. Con la IA, podemos predecir la demanda con mayor precisión, reducir el exceso de existencias, evitar desabastecimientos y, en última instancia, mejorar los resultados de nuestra organización. Exploremos cómo este enfoque no solo aumenta las ventas y la eficiencia operativa, sino que también eleva la satisfacción del cliente al garantizar que los productos estén siempre disponibles cuando sea necesario.

 

Información para mejorar la toma de decisiones en la gestión de inventarios

1. Precisión de pronóstico mejorada Los algoritmos avanzados de aprendizaje automático analizan datos históricos para identificar patrones que los humanos podrían pasar por alto. Técnicas como la agrupación, la detección de cambios de régimen, la detección de anomalías y el análisis de regresión proporcionan información profunda sobre los datos. Medir el error de pronóstico es esencial para perfeccionar los modelos de pronóstico; por ejemplo, técnicas como el error absoluto medio (MAE) y el error cuadrático medio (RMSE) ayudan a cuantificar la precisión de los pronósticos. Las empresas pueden mejorar la precisión monitoreando y ajustando continuamente los pronósticos en función de estas métricas de error. como el Planificador de demanda en un minorista de hardware declarado, "Con las mejoras en nuestros pronósticos y planificación de inventario que permitió Smart Software, hemos podido reducir el stock de seguridad en 20% y al mismo tiempo reducir los desabastecimientos en 35%".

2. Análisis de datos en tiempo real Los sistemas de última generación pueden procesar grandes cantidades de datos en tiempo real, lo que permite a las empresas ajustar sus niveles de inventario de forma dinámica en función de las tendencias actuales de la demanda y las condiciones del mercado. Los algoritmos de detección de anomalías pueden identificar y corregir automáticamente picos o caídas repentinas en la demanda, garantizando que los pronósticos sigan siendo precisos. Una historia de éxito notable proviene de Smart IP&O, que permitió a una empresa reducir el inventario en 20% mientras mantenía los niveles de servicio mediante el análisis continuo de datos en tiempo real y el ajuste de los pronósticos en consecuencia. Destacado Gerente de Materiales de FedEx Tech, "Cualquiera que sea la solicitud, debemos cumplir con nuestro compromiso de servicio al día siguiente: Smart nos permite ajustar el riesgo de nuestro inventario para asegurarnos de que tenemos los productos y piezas disponibles para lograr los niveles de servicio que nuestros clientes requieren".

3. Mejora de la eficiencia de la cadena de suministro Las plataformas tecnológicas inteligentes pueden optimizar toda la cadena de suministro, desde la adquisición hasta la distribución, prediciendo los plazos de entrega y optimizando las cantidades de los pedidos. Esto reduce el riesgo de exceso y falta de existencias. Por ejemplo, al utilizar la gestión de inventario basada en pronósticos, Smart Software ayudó a un fabricante a optimizar su cadena de suministro, reduciendo los tiempos de entrega en 15% y mejorando la eficiencia general. El vicepresidente de operaciones de Procon Pump declaró: "Una de las cosas que me gusta de esta nueva herramienta... es que puedo evaluar las consecuencias de las decisiones sobre el almacenamiento del inventario antes de implementarlas".

4. Toma de decisiones mejorada La IA proporciona información y recomendaciones prácticas, lo que permite a los gerentes tomar decisiones informadas. Esto incluye identificar artículos de baja rotación, pronosticar la demanda futura y optimizar los niveles de existencias. El análisis de regresión, por ejemplo, puede relacionar las ventas con variables externas como la estacionalidad o indicadores económicos, proporcionando una comprensión más profunda de los impulsores de la demanda. Uno de los clientes de Smart Software informó una mejora significativa en los procesos de toma de decisiones, lo que resultó en un aumento de 30% en los niveles de servicio y al mismo tiempo redujo el exceso de inventario en 15%. "Smart IP&O nos permitió modelar la demanda en cada ubicación de almacenamiento y, utilizando una planificación basada en el nivel de servicio, determinar cuánto almacenar para lograr el nivel de servicio que requerimos", señaló el Responsable de Compras en Empresas Seneca.

5. Reducción de costo Al optimizar los niveles de inventario, las empresas pueden reducir los costos de mantenimiento y minimizar las pérdidas por productos obsoletos o caducados. Los sistemas impulsados por IA también reducen la necesidad de realizar comprobaciones manuales de inventario, lo que ahorra tiempo y costes laborales. Un estudio de caso reciente muestra cómo se logró la implementación de la planificación y optimización del inventario (IP&O) dentro de los 90 días posteriores al inicio del proyecto. Durante los seis meses siguientes, IP&O permitió ajustar los parámetros de almacenamiento de varios miles de artículos, lo que resultó en reducciones de inventario de $9,0 millones y al mismo tiempo mantuvo los niveles de servicio objetivo.

 

Al aprovechar algoritmos avanzados y análisis de datos en tiempo real, las empresas pueden mantener niveles óptimos de inventario y mejorar el rendimiento general de su cadena de suministro. La planificación y optimización del inventario (IP&O) es una herramienta poderosa que puede ayudar a su organización a alcanzar estos objetivos. La incorporación de optimización de inventario de última generación en su organización puede generar mejoras significativas en la eficiencia, la reducción de costos y la satisfacción del cliente.

 

 

Las empresas de servicios públicos tienen requisitos únicos de optimización de la cadena de suministro, principalmente garantizando un alto tiempo de actividad al mantener todas las máquinas críticas en funcionamiento continuo. Lograr esto implica mantener una alta disponibilidad de repuestos para garantizar un suministro consistente, confiable y seguro. Además, como entidades reguladas, las empresas de servicios públicos también deben gestionar y controlar cuidadosamente los costos.

Gestionar las cadenas de suministro de manera eficiente

Para mantener un suministro eléctrico fiable a 99.99%⁺ Para niveles de servicio, por ejemplo, las empresas de servicios públicos deben poder responder rápidamente a los cambios en la demanda en el corto plazo y anticipar con precisión la demanda futura. Para ello, deben tener una cadena de suministro bien organizada que les permita comprar los equipos, materiales y servicios necesarios de los proveedores adecuados en el momento adecuado, en las cantidades adecuadas y al precio adecuado.

Hacerlo se ha vuelto cada vez más desafiante en los últimos 3 años.

• Los requisitos de seguridad, confiabilidad y prestación de servicios son más estrictos.
• Las interrupciones en la cadena de suministro, los plazos de entrega impredecibles de los proveedores y los picos intermitentes en el uso de piezas siempre han sido problemáticos, pero ahora son más la regla que la excepción.
• La desregulación a principios de la década de 2000 eliminó las piezas de repuesto de la lista de artículos reembolsados directamente, lo que obligó a las empresas de servicios públicos a pagar las piezas de repuesto directamente con los ingresos.[1]
• La necesidad constante de capital combinada con tasas de interés que aumentan agresivamente significa que los costos se examinan más que nunca.

Como resultado, la optimización de la cadena de suministro (SCO) se ha convertido en una práctica empresarial cada vez más crítica para las empresas de servicios públicos. Para hacer frente a estos desafíos, las empresas de servicios públicos ya no pueden simplemente gestionar su cadena de suministro: deben optimizarla. Y para ello, serán necesarias inversiones en nuevos procesos y sistemas.

[1] Scala et al. “Inventario de Riesgos y Repuestos en Empresas Eléctricas”. Actas de la Conferencia de Investigación de Ingeniería Industrial.

Planificación y optimización de inventario   

Las inversiones específicas en tecnología de optimización de inventario ofrecen un camino a seguir para cada empresa de servicios públicos. Las soluciones de optimización de inventario deben priorizarse porque:

1. Puede implementarse en una fracción del tiempo requerido para iniciativas en otras áreas, como la gestión de almacenes, el diseño de la cadena de suministro y las consolidaciones de compras. No es raro comenzar a generar beneficios después de 90 días y tener una implementación de software completa en menos de 180 días.
2. Puede generar un ROI masivo, con rendimientos 20x y beneficios financieros de siete cifras al año. Al pronosticar mejor el uso de piezas, las empresas de servicios públicos reducirán los costos al comprar solo el inventario necesario mientras controlan el riesgo de desabastecimiento que conduce a tiempos de inactividad y niveles de servicio deficientes.
3. Proporcionar apoyo fundamental para otras iniciativas. Una cadena de suministro sólida se basa en pronósticos de uso sólidos y planes de compra de inventario.

Utilizando análisis predictivos y algoritmos avanzados, la optimización de inventario ayuda a las empresas de servicios públicos a maximizar los niveles de servicio y reducir los costos operativos mediante la optimización de los niveles de inventario de piezas de repuesto. Por ejemplo, una empresa de servicios eléctricos podría usar pronósticos estadísticos para predecir el uso futuro de piezas, realizar auditorías de inventario para identificar el exceso de inventario y aprovechar los resultados analíticos para identificar dónde deben enfocarse primero los esfuerzos de optimización del inventario. Al hacer esto, la empresa de servicios públicos puede garantizar que las máquinas funcionen a niveles óptimos y reducir el riesgo de demoras costosas debido a la falta de repuestos.

Mediante el uso de análisis y datos, puede identificar qué repuestos y equipos es más probable que se necesiten y pedir solo los artículos necesarios. Esto ayuda a garantizar que el equipo tenga un alto tiempo de actividad. Recompensa el monitoreo y el ajuste regulares de los niveles de inventario para que cuando cambien las condiciones operativas, pueda detectar el cambio y ajustarlo en consecuencia. Esto implica que los ciclos de planificación deben operar a un ritmo lo suficientemente alto como para mantenerse al día con las condiciones cambiantes. apalancamiento de pronóstico probabilístico recalibrar las políticas de almacenamiento de repuestos para cada ciclo de planificación garantiza que las políticas de almacenamiento (como los niveles mínimos/máximos) estén siempre actualizadas y reflejen el uso de piezas y los plazos de entrega de los proveedores más recientes.

 

Niveles de servicio y la curva de compensación

El nivel de servicio Curva de compensación relaciona la inversión en inventario con la disponibilidad de artículos medida por el nivel de servicio. El nivel de servicio es la probabilidad de que no ocurra escasez entre el momento en que solicita más existencias y cuando llega al estante. Sorprendentemente, pocas empresas tienen datos sobre esta importante métrica en toda su flota de repuestos.

La curva de compensación del nivel de servicio expone el vínculo entre los costos asociados con los diferentes niveles de servicio y los requisitos de inventario necesarios para alcanzarlos. Saber qué componentes son importantes para mantener altos niveles de servicio es clave para el proceso de optimización y está determinado por varios factores, incluida la estandarización de artículos del inventario, la criticidad, el uso histórico y las órdenes de reparación futuras conocidas. Al comprender esta relación, las empresas de servicios públicos pueden asignar mejor los recursos, como cuando se usan las curvas para identificar áreas donde se pueden reducir los costos sin afectar la confiabilidad del sistema.

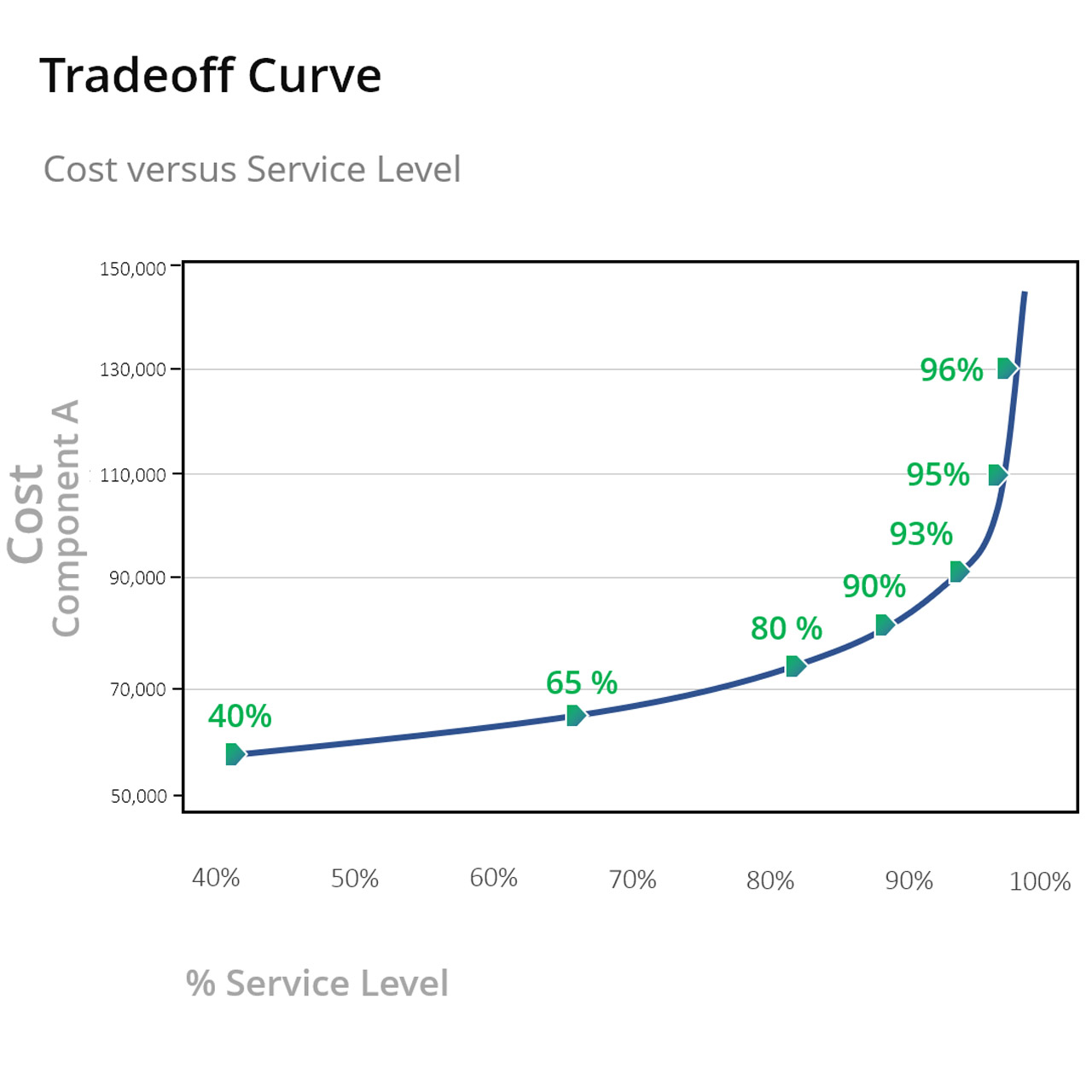
Con el software de optimización de inventario, establecer políticas de almacenamiento es pura conjetura: es posible saber cómo cualquier aumento o disminución afectará los niveles de servicio, además de las estimaciones aproximadas. Nadie sabe realmente cómo se desarrollarán los cambios en términos de inversión en inventarios, costos operativos y costos de escasez. La mayoría de los servicios públicos dependen de métodos de regla general y ajustar arbitrariamente las políticas de almacenamiento de manera reactiva después de que algo haya salido mal, como una gran falta de existencias o una pérdida de inventario. Cuando los ajustes se realizan de esta manera, no hay un análisis basado en hechos que detalle cómo se espera que este cambio afecte las métricas que importan: niveles de servicio y valores de inventario.

El software de optimización de inventario puede calcular las curvas de compensación cuantitativas y detalladas requeridas para tomar decisiones informadas sobre políticas de inventario o incluso recomendar el nivel de servicio objetivo que resulte en el costo operativo general más bajo (la suma de los costos de mantenimiento, pedido y desabastecimiento). Usando este análisis, los grandes aumentos en los niveles de existencias pueden justificarse matemáticamente cuando la reducción prevista en los costos de escasez supera el aumento en la inversión en inventario y los costos de mantenimiento asociados. Al establecer niveles de servicio apropiados y recalibrar las políticas en todas las partes activas una vez en cada ciclo de planificación (al menos una vez al mes), las empresas de servicios públicos pueden minimizar el riesgo de interrupciones mientras controlan los gastos.

Quizás los aspectos más críticos de la respuesta a la avería del equipo son los relacionados con el logro de una arreglo por primera vez lo más rápido posible. Tener los repuestos adecuados disponibles puede ser la diferencia entre completar un solo viaje y aumentar el tiempo medio de reparación, asumir los costos asociados con varias visitas y hacer que las relaciones con los clientes se deterioren.

Con un software moderno, puede comparar el rendimiento anterior y aprovechar los métodos de pronóstico probabilístico para simular el rendimiento futuro. Al someter a prueba sus políticas actuales de almacenamiento de inventario frente a todos los escenarios plausibles de uso futuro de piezas, sabrá de antemano cómo es probable que funcionen las políticas de almacenamiento actuales y propuestas. Cecha un vistazo a nuestra publicación de blog sobre cómo medir la precisión de su pronóstico de nivel de servicio para ayudarlo a evaluar la precisión de las recomendaciones de inventario que los proveedores de software pretenden proporcionar beneficios.

 

 

Aprovechando el análisis avanzado y la IA

Al introducir la automatización, cada empresa de servicios públicos tiene sus propios objetivos que perseguir, pero se debe comenzar evaluando las operaciones actuales para identificar áreas que pueden volverse más efectivas. Algunas empresas pueden priorizar las cuestiones financieras, pero otras pueden priorizar las exigencias regulatorias, como el gasto en energía limpia o cambios en toda la industria, como las redes inteligentes. Las dificultades de cada empresa son únicas, pero el software moderno puede señalar el camino hacia un sistema de gestión de inventario más eficaz que minimice el exceso de inventario y coloque los componentes correctos en los lugares correctos y en el momento adecuado.

En general, las iniciativas de optimización de la cadena de suministro son esenciales para las empresas de servicios públicos que buscan maximizar su eficiencia y reducir sus costos. La tecnología nos permite hacer que el proceso de integración sea perfecto y no es necesario que reemplace su sistema ERP o EAM actual para hacerlo. Solo necesita hacer un mejor uso de los datos que ya tiene.

Por ejemplo, una gran empresa de servicios públicos lanzó una iniciativa estratégica de optimización de la cadena de suministro (SCO) y agregó las mejores capacidades de su clase a través de la selección e integración de aplicaciones comerciales listas para usar. El principal de ellos fue el sistema inteligente de planificación y optimización de inventario (Smart IP&O), que comprende la funcionalidad de previsión de piezas/planificación de demanda y optimización de inventario. En solo 90 días, el sistema de software estaba listo y funcionando, y pronto redujo el inventario en $9,000,000 mientras mantenía la disponibilidad de repuestos a un alto nivel. Puedes leer el caso de estudio aquí La empresa de servicios eléctricos opta por Smart IP&O.

Las empresas de servicios públicos pueden asegurarse de poder gestionar sus suministros de repuestos de una manera eficiente y rentable, preparándolas mejor para el futuro. Con el tiempo, este equilibrio entre oferta y demanda se traduce en una ventaja significativa. Comprender la curva de compensación del nivel de servicio ayuda a comprender los costos asociados con los diferentes niveles de servicio y los requisitos de inventario necesarios para lograrlos. Esto conduce a costos operativos reducidos, inventario optimizado y garantía de que puede satisfacer las necesidades de sus clientes.

 

 

 

​​En un entorno de fabricación altamente configurable, pronosticar productos terminados puede convertirse en una tarea compleja y desalentadora. El número de posibles productos terminados se dispara cuando muchos componentes son intercambiables. Un MRP tradicional nos obligaría a pronosticar cada producto terminado, lo que puede resultar poco realista o incluso imposible. Varias soluciones líderes introducen el concepto de "Planificación BOM", que permite el uso de pronósticos a un nivel superior en el proceso de fabricación. En este artículo, analizaremos esta funcionalidad en Epicor Kinetic y cómo puede aprovecharla con Epicor Smart Inventory Planning and Optimization (Smart IP&O) para adelantarse a su demanda ante esta complejidad.

¿Por qué necesitaría una lista de materiales de planificación?

Tradicionalmente, cada producto terminado o SKU tenía una lista de materiales rígidamente definida. Si almacenamos ese producto y queremos planificar en torno a la demanda pronosticada, pronosticaremos la demanda de esos productos y luego alimentaremos MRP para llevar esta demanda pronosticada desde el nivel del producto terminado hasta sus componentes a través de la lista de materiales.

Sin embargo, muchas empresas ofrecen productos altamente configurables donde los clientes pueden seleccionar opciones sobre el producto que compran. Como ejemplo, recuerde la última vez que compró un teléfono móvil. Elegiste una marca y un modelo, pero a partir de ahí probablemente se te presentaron opciones: ¿qué tamaño de pantalla quieres? ¿Cuánto almacenamiento quieres? ¿Qué color prefiere usted? Si esa empresa quiere tener estos teléfonos móviles listos y disponibles para enviárselos en un tiempo razonable, de repente, ya no solo anticipan la demanda de ese modelo: deben pronosticar ese modelo para cada tipo de tamaño de pantalla, para todas las capacidades de almacenamiento, ¡Para todos los colores y todas las combinaciones posibles de ellos también! Para algunos fabricantes, estas configuraciones pueden dar lugar a cientos o miles de posibles permutaciones de productos terminados.

Puede haber tantas personalizaciones posibles que la demanda a nivel del producto terminado sea completamente impredecible en el sentido tradicional. Es posible que se vendan miles de esos teléfonos móviles cada año, pero para cada configuración posible, la demanda puede ser extremadamente baja y esporádica; tal vez ciertas combinaciones se vendan una vez y nunca más.

Esto a menudo obliga a estas empresas a planificar puntos de reorden y niveles de existencias de seguridad principalmente a nivel de componentes, mientras reaccionan en gran medida a la demanda firme en el nivel de producto terminado a través de MRP. Si bien este es un enfoque válido, carece de una forma sistemática de aprovechar los pronósticos que puedan dar cuenta de la actividad futura anticipada, como promociones, próximos proyectos u oportunidades de ventas. Hacer pronósticos a nivel “configurado” es efectivamente imposible, y tratar de incorporar estos supuestos de pronóstico a nivel de componentes tampoco es factible.

Explicación de la lista de materiales de planificación Aquí es donde entran las listas de materiales de planificación. Quizás el equipo de ventas esté trabajando en una gran oportunidad B2B para ese modelo, o haya una promoción planificada para el Cyber Monday. Si bien no es realista intentar trabajar con esos supuestos para cada configuración posible, hacerlo a nivel de modelo es totalmente factible y tremendamente valioso.

La lista de materiales de planificación puede utilizar una previsión a un nivel superior y luego reducir la demanda en función de proporciones predefinidas para sus posibles componentes. Por ejemplo, el fabricante de teléfonos móviles puede saber que la mayoría de las personas optan por 128 GB de almacenamiento y que muchas menos optan por actualizaciones a 256 GB o 512 GB. La lista de materiales de planificación permite a la organización (por ejemplo) reducir 60% de la demanda a la opción de 128 GB, 30% a la opción de 256 GB y 10% a la opción de 512 GB. Podrían hacer lo mismo con los tamaños de pantalla, los colores u otras personalizaciones disponibles.

La empresa ahora puede centrar su pronóstico en este nivel de modelo, dejando que la lista de materiales de planificación determine la combinación de componentes. Claramente, definir estas proporciones requiere algo de reflexión, pero la planificación de listas de materiales permite efectivamente a las empresas pronosticar lo que de otro modo sería impredecible.

La importancia de un buen pronóstico

Por supuesto, todavía necesitamos un buen pronóstico para cargar en Epicor Kinetic. Como se explica en este artículo, si bien Epicor Kinetic puede importar un pronóstico, a menudo no puede generar uno y, cuando lo hace, tiende a requerir una gran cantidad de configuraciones difíciles de usar que no suelen revisarse, lo que genera pronósticos inexactos. . Por lo tanto, corresponde a la empresa elaborar sus propios conjuntos de pronósticos, a menudo elaborados manualmente en Excel. La elaboración de pronósticos manualmente generalmente presenta una serie de desafíos, que incluyen, entre otros:

• La incapacidad de identificar patrones de demanda como estacionalidad o tendencia.
• Dependencia excesiva de las previsiones de clientes o de ventas.
• Falta de precisión o seguimiento del desempeño.

No importa qué tan bien configurado esté el MRP con sus listas de materiales de planificación cuidadosamente consideradas, un pronóstico deficiente significa una producción deficiente del MRP y desconfianza en el sistema: basura que entra, basura que sale. Siguiendo con el ejemplo de la “compañía de telefonía celular”, sin una forma sistemática de capturar patrones de demanda clave y/o conocimiento del dominio en el pronóstico, MRP nunca podrá verlo.

 

IP&O inteligente: una solución integral

Smart IP&O respalda la planificación en todos los niveles de su lista de materiales, aunque el “soplado” se maneja a través de MRP dentro de Epicor Kinetic. Este es el método que utilizamos para nuestros clientes de Epicor Kinetic, que es sencillo y efectivo:

• Planificador de la demanda: La plataforma contiene una aplicación de pronóstico especialmente diseñada llamada Smart Demand Planner que utilizará para pronosticar la demanda de sus productos manufacturados (generalmente productos terminados). Genera pronósticos estadísticos, permite a los planificadores realizar ajustes y/o incorporar otros pronósticos (como pronósticos de ventas o de clientes) y realiza un seguimiento de la precisión. El resultado de esto es un pronóstico que ingresa a la entrada de pronóstico dentro de Epicor Kinetic, donde MRP lo recogerá. Posteriormente, MRP utilizará la demanda en el nivel del producto terminado y también eliminará los requisitos de material a través de la lista de materiales, de modo que la demanda también se reconozca en niveles más bajos.
• Optimización del inventario: Puede utilizar simultáneamente la optimización inteligente de inventario para establecer niveles mínimos/máximos/de seguridad tanto para cualquier producto terminado que fabrique para almacenar (si corresponde; algunos de nuestros clientes operan exclusivamente bajo pedido según la demanda firme), así como para materias primas. materiales. La clave aquí es que a nivel de materia prima, Smart aprovechará la demanda de uso del trabajo, los tiempos de entrega de los proveedores, etc., para optimizar estos parámetros y al mismo tiempo utilizará los pedidos/envíos de ventas como demanda en el nivel del producto terminado. Smart maneja estas múltiples entradas de demanda de manera elegante a través de la integración bidireccional con Epicor Kinetic.

Cuando se ejecuta MRP, compara la oferta y la demanda (que, una vez más, incluye la demanda de materia prima extraída del pronóstico del producto terminado) con los niveles mínimo/máximo/de seguridad que ha establecido para sugerir PO y sugerencias de trabajo.

 

Amplíe Epicor Kinetic con Smart IP&O

Smart IP&O está diseñado para ampliar su sistema Epicor Kinetic con muchas soluciones integradas de planificación de la demanda y optimización de inventario. Por ejemplo, puede generar pronósticos estadísticos automáticamente para una gran cantidad de artículos, permite ajustes de pronóstico intuitivos, realiza un seguimiento de la precisión del pronóstico y, en última instancia, le permite generar verdaderos pronósticos basados en consenso para anticipar mejor las necesidades de sus clientes.

Gracias a las jerarquías de productos altamente flexibles, Smart IP&O se adapta perfectamente a la previsión en el nivel de planificación de la lista de materiales, por lo que puede capturar patrones clave e incorporar conocimiento empresarial en los niveles más importantes. Además, puede analizar e implementar niveles óptimos de existencias de seguridad en cualquier nivel de su lista de materiales.

Aprovechar las capacidades de planificación de BOM de Epicor Kinetic junto con las funciones avanzadas de optimización de inventario y pronóstico de Smart IP&O garantiza que pueda satisfacer la demanda de manera eficiente y precisa, independientemente de la complejidad de las configuraciones de su producto. Esta sinergia no sólo mejora la precisión de los pronósticos, sino que también fortalece la eficiencia operativa general, ayudándole a mantenerse a la vanguardia en un mercado competitivo.

 

 

Creemos que la vanguardia del análisis de la cadena de suministro es el desarrollo de gemelos digitales de sistemas de inventario. Estos gemelos toman la forma de modelos de eventos discretos que utilizan la simulación Monte Carlo para generar y optimizar toda la gama de riesgos operativos. También afirmamos que nosotros y nuestros colegas de Smart Software hemos desempeñado un papel enorme en la creación de esa vanguardia. Pero no estamos solos: hay un pequeño número de otras empresas de software en todo el mundo que se están poniendo al día.

Entonces, ¿qué sigue para el análisis de la cadena de suministro? ¿Dónde está la próxima frontera? Podría implicar algún tipo de modelo de red neuronal de un sistema de distribución. Pero daríamos mejores probabilidades a una extensión de nuestros modelos de vanguardia de sistemas de inventario de “escalón único” a sistemas de inventario de “escalones múltiples”.

Las Figuras 1 y 2 ilustran la distinción entre sistemas de escalón único y múltiple. La Figura 1 muestra un fabricante que depende de una Fuente para reponer su stock de repuestos o componentes. Cuando se avecina un desabastecimiento, el fabricante solicita reabastecimiento de existencias a la Fuente.

Figura 1: Un sistema de inventario de un solo escalón

 

Los modelos de escalón único no incluyen explícitamente detalles de la Fuente. Sigue siendo un misterio, un fantasma invisible cuya única característica relevante es el tiempo aleatorio que tarda en responder a una solicitud de reabastecimiento. Es importante destacar que se supone implícitamente que la Fuente nunca se agota. Esa suposición puede ser “suficientemente buena” para muchos propósitos, pero no puede ser literalmente cierta. Se maneja incorporando eventos de desabastecimiento de proveedores en la distribución del tiempo de entrega de reabastecimiento. Rechazar ese supuesto es la razón fundamental para el modelado multiescalón.

La Figura 2 muestra un sistema de inventario simple de dos escalones. Cambia los dominios de la fabricación a la distribución. Hay múltiples almacenes (WH) que dependen de un centro de distribución (DC) para el reabastecimiento. Ahora el DC es una parte explícita del modelo. Tiene una capacidad finita para procesar pedidos y requiere sus propios protocolos de reordenamiento. El DC se reabastece desde arriba en la cadena desde una Fuente. La Fuente podría ser el fabricante del artículo del inventario o quizás un “CD regional” o algo similar, pero ¿adivinen qué? – es otro fantasma. Al igual que en el modelo de un solo escalón, este fantasma tiene una característica visible: la distribución de probabilidad de su tiempo de reabastecimiento. (El chiste de un famoso chiste de física es "Pero señora, hay tortugas hasta abajo". En nuestro caso, "Son fantasmas hasta arriba").

Figura 2: Un sistema de inventario de dos niveles

 

El problema del diseño y optimización de procesos es mucho más difícil con dos niveles. La dificultad no es sólo la adición de dos parámetros de control más para cada WH (por ejemplo, un mínimo y un máximo para cada uno) más los mismos dos parámetros para el DC. Más bien, la parte más difícil es modelar la interacción entre los WH. En el modelo de un solo nivel, cada WH opera en su propio pequeño mundo y nunca escucha "Lo siento, estamos agotados" de la Fuente fantasmal. Pero en un sistema de dos niveles, hay múltiples WH que compiten por el reabastecimiento desde su DC compartido. Esta competencia crea la principal dificultad analítica: los WH no pueden modelarse de forma aislada sino que deben analizarse simultáneamente. Por ejemplo, si un DC da servicio a diez WH, hay 2+10×2 = 22 parámetros de control de inventario cuyos valores deben calcularse. En lenguaje nerd: no es trivial resolver un problema de optimización discreta restringido de 22 variables que tiene una función objetivo estocástica.

Si elegimos el diseño de sistema incorrecto, descubrimos un nuevo fenómeno inherente a los sistemas de múltiples niveles, que informalmente llamamos "fusión" o "catástrofe". En este fenómeno, el CD no puede satisfacer las demandas de reabastecimiento de los WH, por lo que eventualmente crea desabastecimientos a nivel de almacén. Luego, las solicitudes de reabastecimiento cada vez más frenéticas del WH agotan el inventario en el DC, que inicia sus propias solicitudes de reabastecimiento en pánico desde el DC regional. Si el CD regional tarda demasiado en reponer el CD, entonces todo el sistema se disuelve en una tragedia de desabastecimiento.

Una solución al problema de la fusión es sobrediseñar el CD para que casi nunca se agote, pero eso puede ser muy costoso, razón por la cual existe un CD regional en primer lugar. Por lo tanto, cualquier diseño de sistema asequible tiene un CC que sea lo suficientemente bueno como para durar mucho tiempo entre fusiones. Esta perspectiva implica un nuevo tipo de indicador clave de desempeño (KPI), como “La probabilidad de colapso dentro de X años es inferior al Y por ciento”.

La próxima frontera requerirá nuevos métodos y nuevas métricas, pero ofrecerá una nueva forma de diseñar y optimizar los sistemas de distribución. Nuestra fábrica de zorrillos ya está generando prototipos. Mira este espacio.