Si sigues las noticias sobre análisis de la cadena de suministro, se encontrará con más frecuencia con la frase “pronóstico probabilístico”. Si esta frase es desconcertante, sigue leyendo.
Probablemente ya sepa lo que significa "pronóstico". Y probablemente también sepa que parece haber muchas maneras diferentes de hacerlo. Y probablemente haya escuchado pequeñas frases picantes como "todo pronóstico es incorrecto". Así que sabes que algún tipo de matemágica podría calcular que "el pronóstico es que venderá 100 unidades el próximo mes", y luego podría vender 110 unidades, en cuyo caso tiene un error de pronóstico 10%.
Es posible que no sepa que lo que acabo de describir es un tipo particular de pronóstico llamado "pronóstico puntual". Un pronóstico puntual se llama así porque consta de un solo número (es decir, un punto en la recta numérica, si recuerda la recta numérica de su juventud).
Pronósticos puntuales tienen una virtud: Son simples. También tienen un defecto: dan lugar a afirmaciones sarcásticas como “todas las previsiones están equivocadas”. Es decir, en la mayoría de los casos realistas, es poco probable que el valor real sea exactamente igual al pronóstico. (Lo cual no es gran cosa si el pronóstico es lo suficientemente cercano).
Esto nos lleva al "pronóstico probabilístico". Este enfoque es un paso adelante, porque en lugar de producir un pronóstico de un solo número (punto), produce una distribución de probabilidad para el pronóstico. Y a diferencia de los modelos extrapolativos tradicionales que se basan únicamente en los datos históricos, los pronósticos probabilísticos tienen la capacidad de simular valores futuros que no están anclados al pasado.
“Distribución de probabilidad” es una frase prohibitiva, que evoca algunas matemáticas arcanas de las que quizás hayas oído hablar pero que nunca hayas estudiado. Afortunadamente, la mayoría de los adultos tienen suficiente experiencia de vida para tener una comprensión intuitiva del concepto. Cuando se desglosa, es bastante sencillo de entender.
Imagina el simple acto de lanzar dos monedas. Puede llamar a esto diversión inofensiva, pero yo lo llamo un "experimento probabilístico". El número total de caras que salgan en las dos monedas será cero, uno o dos. Lanzar dos monedas es un "experimento aleatorio". El número resultante de cabezas es una "variable aleatoria". Tiene una “distribución de probabilidad”, que no es más que una tabla de la probabilidad de que la variable aleatoria tenga alguno de sus posibles valores. La probabilidad de obtener dos caras cuando las monedas son justas resulta ser ¼, al igual que la probabilidad de que no salga cara. La probabilidad de una cara es ½.
El mismo enfoque puede describir una variable aleatoria más interesante, como la demanda diaria de una pieza de repuesto. La Figura 2 muestra tal distribución de probabilidad. Se calculó mediante la compilación de tres años de datos de demanda diaria de una determinada parte utilizada en un instrumento científico vendido a hospitales.
Figura 1: La distribución de probabilidad de la demanda diaria de una determinada pieza de repuesto
La distribución de la Figura 1 se puede considerar como un pronóstico probabilístico de la demanda en un solo día. Para esta parte en particular, vemos que es muy probable que el pronóstico sea cero (probabilidad 97%), pero a veces será para un puñado de unidades, y una vez cada tres años será para veinte unidades. Aunque el pronóstico más probable es cero, querrás tener algunos a mano si esta parte fuera crítica ("... por falta de un clavo...")
Ahora usemos esta información para hacer un pronóstico probabilístico más complicado. Suponga que tiene tres unidades a mano. ¿Cuántos días tardará en no tener ninguno? Hay muchas respuestas posibles, que van desde un solo día (si obtiene inmediatamente una demanda de tres o más) hasta un número muy grande (ya que 97% de días no ven demanda). El análisis de esta pregunta es un poco complicado debido a todas las formas en que esta situación puede desarrollarse, pero la respuesta final que es más informativa será una distribución de probabilidad. Resulta que el número de días hasta que no quedan unidades en stock tiene la distribución que se muestra en la Figura 2.
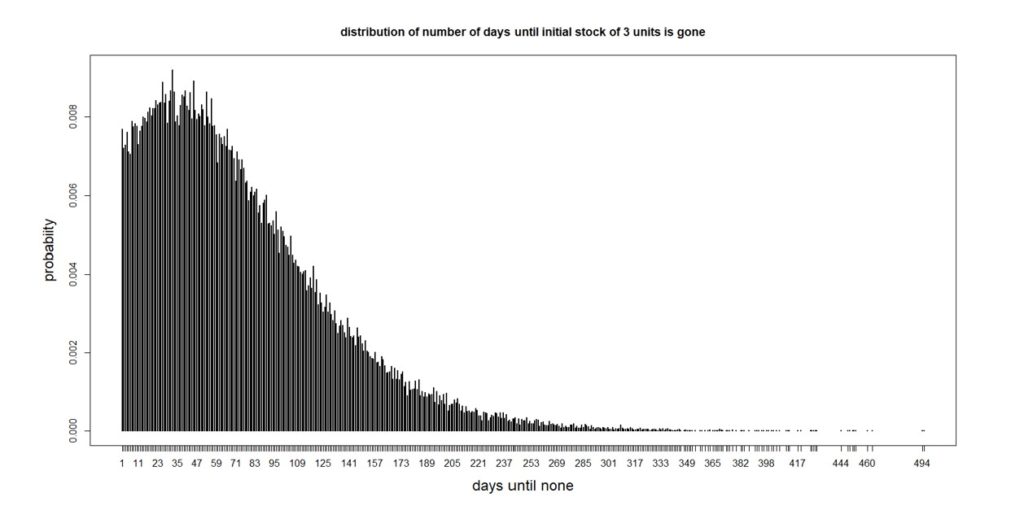
Figura 2: Distribución del número de días hasta que se acaban las tres unidades
El promedio de días es 74, lo que sería un pronóstico puntual, pero hay mucha variación alrededor del promedio. Desde la perspectiva de la gestión de inventario, cabe destacar que existe una posibilidad de 25% de que todas las unidades se hayan ido después de 32 días. Entonces, si decidió pedir más cuando solo tenía tres en el estante, sería bueno que el proveedor se los entregue antes de que haya pasado un mes. Si no pudieran, tendría la posibilidad de agotarse el 75%, lo que no es bueno para una pieza crítica.
El análisis detrás de la Figura 2 implicó hacer algunas suposiciones que eran convenientes pero no necesarias si no eran ciertas. Los resultados provinieron de un método llamado "simulación de Monte Carlo", en el que comenzamos con tres unidades, elegimos una demanda aleatoria de la distribución en la Figura 1, la restamos de las existencias actuales y continuamos hasta que se agoten las existencias, registrando cuántas Pasaron los días antes de que se acabara. Repitiendo este proceso 100.000 veces se produjo la Figura 2.
Las aplicaciones de la simulación de Monte Carlo se extienden a problemas de alcance aún mayor que el ejemplo anterior de "cuándo nos quedamos sin". Especialmente importantes son los pronósticos de Monte Carlo de la demanda futura. Si bien el resultado habitual de los pronósticos es un conjunto de pronósticos puntuales (por ejemplo, la demanda unitaria esperada durante los próximos doce meses), sabemos que la demanda real podría desarrollarse de varias maneras. La simulación podría usarse para producir, digamos, mil conjuntos posibles de 365 demandas diarias.
Este conjunto de escenarios de demanda expondría de manera más completa el rango de posibles situaciones con las que tendría que lidiar un sistema de inventario. Este uso de la simulación se denomina "prueba de estrés", porque expone un sistema a una variedad de escenarios variados pero realistas, incluidos algunos desagradables. Luego, esos escenarios se ingresan en modelos matemáticos del sistema para ver qué tan bien los manejará, como se refleja en los indicadores clave de rendimiento (KPI). Por ejemplo, en esos mil años simulados de operación, ¿cuántos desabastecimientos hay en el peor año? el año promedio? el mejor año? De hecho, ¿cuál es la distribución de probabilidad completa del número de desabastecimientos en un año y cuál es la distribución de su tamaño?
Las Figuras 3 y 4 ilustran el modelado probabilístico de un sistema de control de inventario que convierte los desabastecimientos en pedidos atrasados. El sistema simulado usa una política de control Min/Max con Min = 10 unidades y Max = 20 unidades.
La Figura 3 muestra un año simulado de operaciones diarias en cuatro parcelas. El primer gráfico muestra un patrón particular de demanda diaria aleatoria en el que la demanda promedio aumenta constantemente de lunes a viernes pero desaparece los fines de semana. La segunda gráfica muestra el número de unidades disponibles cada día. Tenga en cuenta que hay una docena de veces durante este año simulado cuando el inventario se vuelve negativo, lo que indica falta de existencias. El tercer gráfico muestra el tamaño y el momento de los pedidos de reabastecimiento. La cuarta gráfica muestra el tamaño y el tiempo de los pedidos pendientes. La información de estos gráficos se puede traducir en estimaciones de inversión en inventario, unidades promedio disponibles, costos de mantenimiento, costos de pedido y costos de escasez.
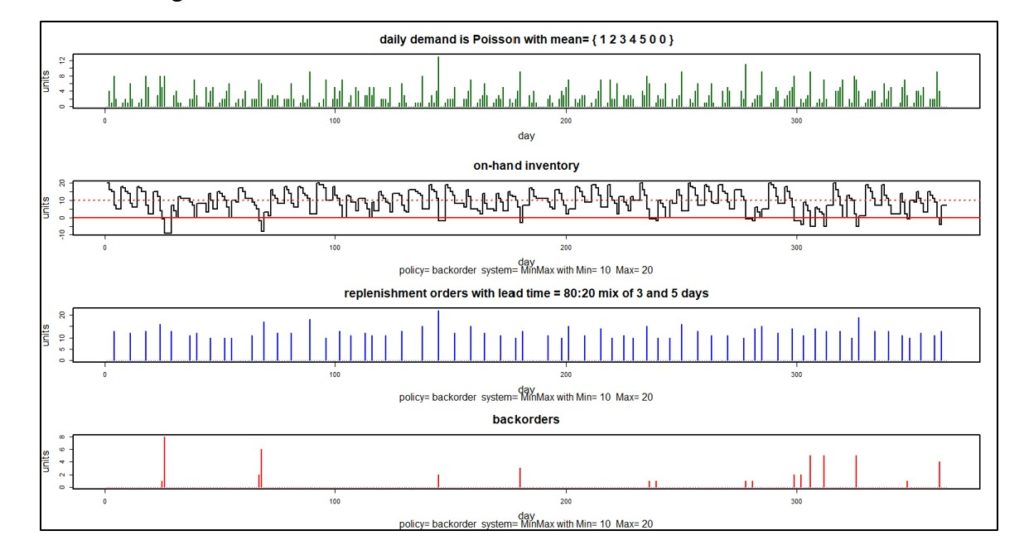
Figura 3: Un año simulado de operación del sistema de inventario
La figura 3 muestra uno de mil años simulados. Cada año tendrá diferentes demandas diarias, lo que dará como resultado diferentes valores de métricas como unidades disponibles y los diversos componentes del costo operativo. La figura 4 traza la distribución de 1000 valores simulados de cuatro KPI. La simulación de 1000 años de operación imaginada expone el rango de resultados posibles para que los planificadores puedan tener en cuenta no solo los resultados promedio, sino también ver los valores en el mejor y el peor de los casos.
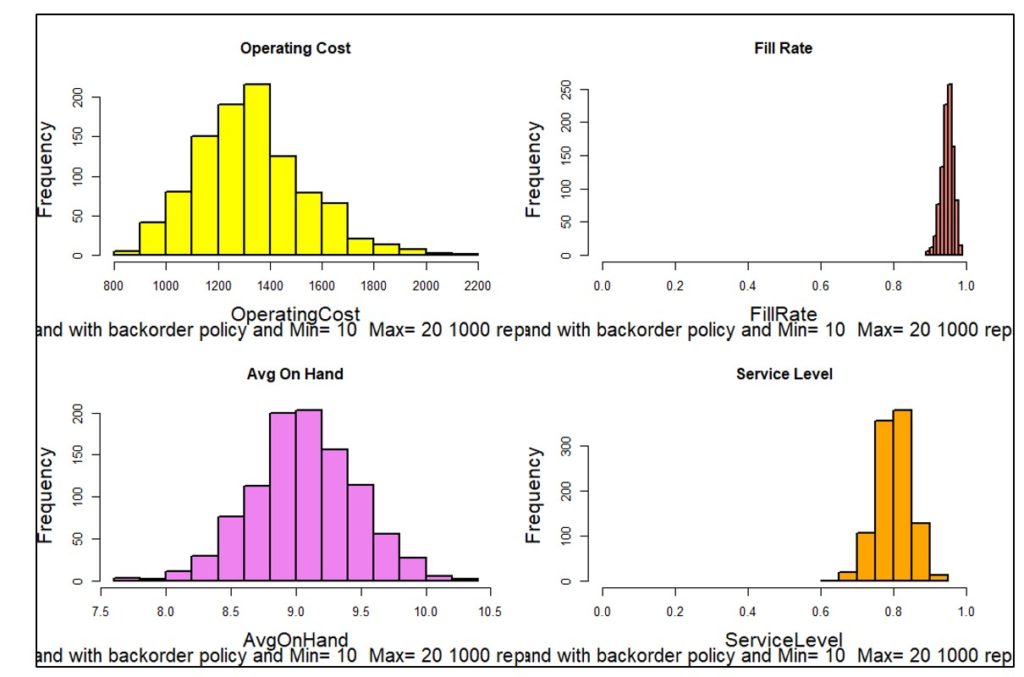
Figura 4: Distribuciones de cuatro KPI basadas en 1000 simulaciones
La simulación de Monte Carlo es un enfoque de pronóstico probabilístico de pocas matemáticas y altos resultados: muy práctico y fácil de explicar. Los métodos avanzados de pronóstico probabilístico empleados por Smart Software amplían la simulación estándar de Monte Carlo y producen estimaciones extremadamente precisas de los niveles de inventario requeridos.
Artículos Relacionados
Haga de la optimización de inventario impulsada por IA un aliado para su organización
En este blog, exploraremos cómo las organizaciones pueden lograr una eficiencia y precisión excepcionales con la optimización del inventario impulsada por la IA. Los métodos tradicionales de gestión de inventario a menudo resultan insuficientes debido a su naturaleza reactiva y su dependencia de procesos manuales. Mantener niveles óptimos de inventario es fundamental para satisfacer la demanda de los clientes y minimizar los costos. La introducción de la optimización del inventario impulsada por la IA puede reducir significativamente la carga de los procesos manuales, brindando alivio a los gerentes de la cadena de suministro de tareas tediosas.
Escenarios de demanda diaria
En este Videoblog explicaremos cómo la previsión de series temporales se ha convertido en una herramienta fundamental, especialmente a nivel diario, en la que Smart Software ha sido pionero desde sus inicios hace más de cuarenta años. La evolución de las prácticas comerciales de incrementos temporales anuales a incrementos temporales más refinados, como el análisis de datos mensual y ahora diario, ilustra un cambio significativo en las estrategias operativas.
Juego constructivo con gemelos digitales
Aquellos de ustedes que siguen temas candentes estarán familiarizados con el término "gemelo digital". Aquellos que han estado demasiado ocupados con el trabajo tal vez quieran seguir leyendo y ponerse al día. Si bien existen varias definiciones de gemelo digital, aquí hay una que funciona bien: un gemelo digital es una copia virtual dinámica de un activo físico, proceso, sistema o entorno que se parece y se comporta de manera idéntica a su contraparte del mundo real. Un gemelo digital ingiere datos y replica procesos para que pueda predecir posibles resultados de rendimiento y problemas que podría experimentar el producto del mundo real.
Mensajes recientes
Gestión de inventario basada en pronósticos para una mejor planificaciónForecast-based inventory management, or MRP (Material Requirements Planning) logic, is a forward-planning method that helps businesses meet demand without overstocking or understocking. By anticipating demand and adjusting inventory levels, it maintains a balance between meeting customer needs and minimizing excess inventory costs. This approach optimizes operations, reduces waste, and enhances customer satisfaction. […]
Haga de la optimización de inventario impulsada por IA un aliado para su organizaciónEn este blog, exploraremos cómo las organizaciones pueden lograr una eficiencia y precisión excepcionales con la optimización del inventario impulsada por la IA. Los métodos tradicionales de gestión de inventario a menudo resultan insuficientes debido a su naturaleza reactiva y su dependencia de procesos manuales. Mantener niveles óptimos de inventario es fundamental para satisfacer la demanda de los clientes y minimizar los costos. La introducción de la optimización del inventario impulsada por la IA puede reducir significativamente la carga de los procesos manuales, brindando alivio a los gerentes de la cadena de suministro de tareas tediosas. […]
La importancia de definiciones claras de niveles de servicio en la gestión de inventarioEl software de optimización de inventario que respalda el análisis hipotético expondrá el equilibrio entre los desabastecimientos y los costos excesivos de los distintos objetivos de nivel de servicio. Pero primero es importante identificar cómo se interpretan, miden y reportan los “niveles de servicio”. Esto evitará la falta de comunicación y la falsa sensación de seguridad que puede desarrollarse cuando se utilizan definiciones menos estrictas. Definir claramente cómo se calcula el nivel de servicio pone a todas las partes interesadas en la misma página. Esto facilita una mejor toma de decisiones. […]
Utilidades preparadas para el futuro: análisis avanzados para la optimización de la cadena de suministroLos servicios públicos en los campos de la electricidad, el gas natural, el agua urbana y las telecomunicaciones requieren muchos activos y dependen de una infraestructura física que debe mantenerse, actualizarse y mejorarse adecuadamente con el tiempo. Maximizar el tiempo de actividad de los activos y la confiabilidad de la infraestructura física exige una gestión eficaz del inventario, la previsión de piezas de repuesto y la gestión de proveedores. Una empresa de servicios públicos que ejecuta estos procesos de manera efectiva superará a sus pares, brindará mejores retornos para sus inversores y mayores niveles de servicio para sus clientes, al mismo tiempo que reducirá su impacto ambiental. […]
El costo de la planificación con hojas de cálculoLas empresas que dependen de hojas de cálculo para la planificación de la demanda, la previsión y la gestión de inventario a menudo se ven limitadas por las limitaciones inherentes de las hojas de cálculo. Esta publicación examina los inconvenientes de los enfoques tradicionales de gestión de inventario causados por las hojas de cálculo y sus costos asociados, comparándolos con los importantes beneficios que se obtienen al adoptar tecnologías de planificación de última generación. […]
Optimización de inventario para fabricantes, distribuidores y MRO
- Utilidades preparadas para el futuro: análisis avanzados para la optimización de la cadena de suministroLos servicios públicos en los campos de la electricidad, el gas natural, el agua urbana y las telecomunicaciones requieren muchos activos y dependen de una infraestructura física que debe mantenerse, actualizarse y mejorarse adecuadamente con el tiempo. Maximizar el tiempo de actividad de los activos y la confiabilidad de la infraestructura física exige una gestión eficaz del inventario, la previsión de piezas de repuesto y la gestión de proveedores. Una empresa de servicios públicos que ejecuta estos procesos de manera efectiva superará a sus pares, brindará mejores retornos para sus inversores y mayores niveles de servicio para sus clientes, al mismo tiempo que reducirá su impacto ambiental. […]
Ley de centrado: sincronización, precio y confiabilidad de los repuestosEn este artículo, lo guiaremos a través del proceso de elaboración de un plan de inventario de repuestos que priorice las métricas de disponibilidad, como los niveles de servicio y las tasas de cumplimiento, al tiempo que garantiza la rentabilidad. Nos centraremos en un enfoque para la planificación de inventario llamado Optimización de inventario basada en el nivel de servicio. A continuación, analizaremos cómo determinar qué piezas debe incluir en su inventario y cuáles podrían no ser necesarias. Por último, exploraremos formas de mejorar consistentemente su plan de inventario basado en el nivel de servicio. […]
Por qué las empresas de MRO necesitan software complementario de planificación e inventario de piezas de servicioLas organizaciones MRO existen en una amplia gama de industrias, incluido el transporte público, los servicios eléctricos, las aguas residuales, la energía hidroeléctrica, la aviación y la minería. Para realizar su trabajo, los profesionales de MRO utilizan sistemas de gestión de activos empresariales (EAM) y planificación de recursos empresariales (ERP). Estos sistemas están diseñados para realizar muchos trabajos. Dadas sus características, costo y amplios requisitos de implementación, se supone que los sistemas EAM y ERP pueden hacerlo todo. En esta publicación, resumimos la necesidad de un software complementario que aborde análisis especializados para la optimización del inventario, la previsión y la planificación de piezas de servicio. […]
5 pasos para mejorar el impacto financiero de la planificación de repuestosEn el competitivo panorama empresarial actual, las empresas buscan constantemente formas de mejorar su eficiencia operativa y generar mayores ingresos. La optimización de la gestión de repuestos es un aspecto que a menudo se pasa por alto y que puede tener un impacto financiero significativo. Las empresas pueden mejorar la eficiencia general y generar importantes rendimientos financieros mediante la gestión eficaz del inventario de piezas de repuesto. Este artículo explorará las implicaciones económicas de la gestión optimizada de repuestos y cómo invertir en software de optimización de inventario y planificación de la demanda puede proporcionar una ventaja competitiva. […]
