Het voorspellen van voorraadbehoeften is een gespecialiseerde variant van prognoses die zich richt op de bovenkant van het bereik van mogelijke toekomstige vraag.

Beschouw voor de eenvoud het probleem van het voorspellen van de voorraadbehoeften voor slechts één periode vooruit, bijvoorbeeld één dag vooruit. Meestal bestaat de taak van forecasting uit het schatten van het meest waarschijnlijke of gemiddelde niveau van de productvraag. Als de beschikbare voorraad echter gelijk is aan de gemiddelde vraag, bestaat er een kans van ongeveer 50% dat de vraag de voorraad overtreft en resulteert in verloren omzet en/of verloren goede wil. Het instellen van het voorraadniveau op bijvoorbeeld tien keer de gemiddelde vraag zal waarschijnlijk het probleem van voorraadtekorten elimineren, maar zal net zo zeker resulteren in oplopende voorraadkosten.

De truc van voorraadoptimalisatie is om een bevredigende balans te vinden tussen voldoende voorraad hebben om aan de meeste vraag te voldoen zonder al te veel middelen in het proces vast te leggen. Meestal is de oplossing een combinatie van zakelijk inzicht en statistieken. Het beoordelende deel is het definiëren van een acceptabel voorraadserviceniveau, zoals het direct uit voorraad voldoen aan 95% vraag. Het statistische deel is om het 95e percentiel van de vraag te schatten.

Wanneer niet omgaan met Intermittent demandkunt u het vereiste voorraadniveau vaak schatten door uit te gaan van een klokvormige (normale) vraagcurve, waarbij u zowel het midden als de breedte van de klokcurve schat, en vervolgens een standaard statistische formule gebruikt om het gewenste percentiel te schatten. Het verschil tussen het gewenste voorraadniveau en het gemiddelde vraagniveau wordt de ‘veiligheidsvoorraad’ genoemd, omdat deze beschermt tegen de mogelijkheid van voorraadtekorten.

Bij een intermitterende vraag is de klokvormige curve een zeer slechte benadering van de statistische verdeling van de vraag. In dit speciale geval maakt Smart gebruik van gepatenteerde technologie voor intermitterende vraag die is ontworpen om de marges nauwkeurig te voorspellen en een betere schatting te maken van de veiligheidsvoorraad die nodig is om het vereiste voorraadserviceniveau te bereiken.

Overzicht

De geavanceerde supply chain-analyse van Smart Software maakt gebruik van meerdere geavanceerde methoden. Twee van de belangrijkste zijn "statistische bootstrapping" en "Monte Carlo-simulatie". Omdat er bij beide veel willekeurige getallen rondvliegen, raken mensen soms in de war over wat wat is en waar ze goed voor zijn. Vandaar deze notitie. Waar het op neerkomt: statistische bootstrapping genereert vraagscenario's voor prognoses. Monte Carlo-simulatie gebruikt de scenario's voor voorraadoptimalisatie.

Opstarten

Bootstrapping, ook wel "resampling" genoemd, is een methode van computationele statistieken die we gebruiken om vraagscenario's voor prognoses te creëren. De essentie van het prognoseprobleem is het blootleggen van mogelijke toekomsten waarmee uw bedrijf te maken kan krijgen, zodat u kunt uitzoeken hoe u bedrijfsrisico's kunt beheersen. Traditionele prognosemethoden richten zich op het berekenen van de "meest waarschijnlijke" toekomst, maar ze geven niet het volledige risicobeeld weer. Bootstrapping biedt een onbeperkt aantal realistische wat-als-scenario's.

Bootstrapping doet dit zonder onrealistische aannames te doen over de vraag, dwz dat deze niet intermitterend is, of dat deze een klokvormige verdeling van groottes heeft. Die aannames zijn krukken om de wiskunde eenvoudiger te maken, maar de bootstrap is een procedure, geen vergelijking, dus dergelijke vereenvoudigingen zijn niet nodig.

Voor het eenvoudigste vraagtype, dat een stabiele willekeur is zonder seizoensgebondenheid of trend, is bootstrapping doodeenvoudig. Om een redelijk idee te krijgen van wat een enkele toekomstige vraagwaarde zou kunnen zijn, kiest u willekeurig een van de historische eisen. Om een vraagscenario te creëren, maakt u meerdere willekeurige selecties uit het verleden en rijgt u ze aan elkaar. Klaar. Het is mogelijk om wat meer realisme toe te voegen door de gevraagde waarden te "jitteren", dwz een beetje extra willekeur aan elke waarde toe te voegen of af te trekken, maar zelfs dat is eenvoudig.

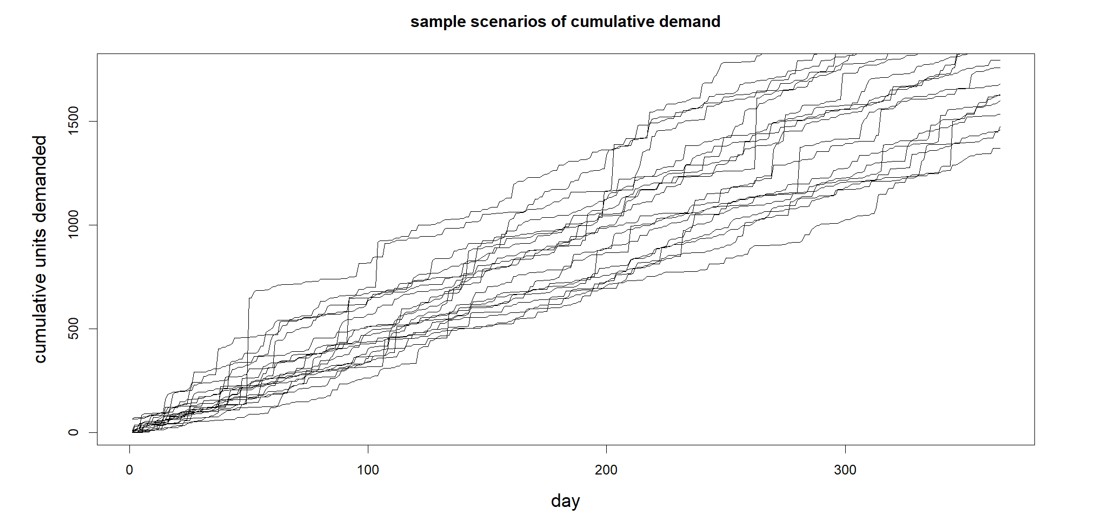
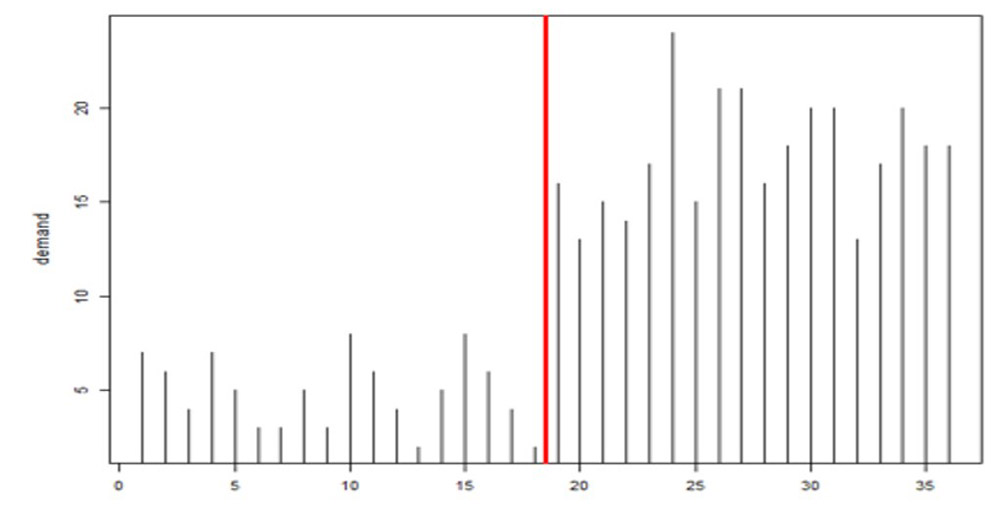
Figuur 1 toont een eenvoudige bootstrap. De eerste regel is een korte reeks historische vraag naar een SKU. De volgende regels tonen scenario's van toekomstige vraag die zijn gemaakt door willekeurig waarden uit de vraaggeschiedenis te selecteren. De volgende drie eisen kunnen bijvoorbeeld zijn (0, 14, 6), of (2, 3, 5), enz.

Afbeelding 1: voorbeeld van vraagscenario's gegenereerd door een eenvoudige bootstrap

Bewerkingen met een hogere frequentie, zoals dagelijkse prognoses, brengen complexere vraagpatronen met zich mee, zoals dubbele seizoensgebondenheid (bijv. dag van de week en maand van het jaar) en/of trend. Dit daagde ons uit om een nieuwe generatie bootstrapping-algoritmen uit te vinden. We hebben onlangs een Amerikaans patent gewonnen voor deze doorbraak, maar de essentie is zoals hierboven beschreven.

Monte Carlo simulatie

Monte Carlo staat bekend om zijn casino's, die net als bootstrapping het idee van willekeur oproepen. Monte Carlo-methoden gaan ver terug, maar de moderne impuls kwam met de noodzaak om wat harige berekeningen te maken over waar neutronen zouden vliegen als een A-bom ontploft.

De essentie van Monte Carlo-analyse is deze: “Ons probleem is te ingewikkeld om te analyseren met vergelijkingen van papier en potlood. Dus, laten we een computerprogramma schrijven dat de individuele stappen van het proces codeert, de willekeurige elementen erin stoppen (bijvoorbeeld welke kant een neutron op schiet), het opwinden en kijken hoe het gaat. Aangezien er veel willekeur is, laten we het programma een ontelbaar aantal keren uitvoeren en het gemiddelde van de resultaten nemen.”

Als we deze benadering toepassen op voorraadbeheer, hebben we een andere reeks willekeurig voorkomende gebeurtenissen: een vraag van een bepaalde omvang komt bijvoorbeeld op een willekeurige dag binnen, een aanvulling van een bepaalde omvang arriveert na een willekeurige doorlooptijd, we snijden een aanvullings-PO van een bepaalde maat wanneer de voorraad daalt tot of onder een bepaald bestelpunt. We coderen de logica die deze gebeurtenissen met elkaar in verband brengt in een programma. We voeden het met een willekeurige vraagvolgorde (zie bootstrapping hierboven), voeren het programma een tijdje uit, laten we zeggen een jaar dagelijkse bewerkingen, berekenen prestatiestatistieken zoals Fill Rate en Average On Hand-inventaris, en "gooi de dobbelstenen" door het opnieuw uit te voeren het programma vele malen en het gemiddelde van de resultaten van vele gesimuleerde jaren. Het resultaat is een goede inschatting van wat er gebeurt als we belangrijke managementbeslissingen nemen: “Als we het bestelpunt op 10 eenheden zetten en de bestelhoeveelheid op 15 eenheden, kunnen we een serviceniveau verwachten van 89% en een gemiddelde beschikbaarheid van 21 eenheden.” Wat de simulatie voor ons doet, is het blootleggen van de gevolgen van managementbeslissingen op basis van realistische vraagscenario's en solide wiskunde. Het giswerk is weg.

Figuur 2 toont enkele van de innerlijke werkingen van een Monte Carlo-simulatie van een voorraadsysteem in vier panelen. Het systeem gebruikt een Min/Max voorraadbeheerbeleid met Min=10 en Max=25. Nabestellingen zijn niet toegestaan: u heeft het goed of u verliest het bedrijf. Doorlooptijden voor aanvulling zijn meestal 7 dagen, maar soms ook 14. Deze simulatie duurde een jaar.

Het eerste paneel toont een complex willekeurig vraagscenario waarin er geen vraag is in het weekend, maar de vraag over het algemeen elke dag toeneemt van maandag tot en met vrijdag. Het tweede paneel toont het willekeurige aantal beschikbare eenheden, dat ebt en vloeit met elke aanvullingscyclus. Het derde paneel toont de willekeurige groottes en tijdstippen van aanvullingsorders die binnenkomen van de leverancier. Het laatste paneel toont de onbevredigde vraag die de klantrelaties in gevaar brengt. Dit soort detail kan erg handig zijn om inzicht te krijgen in de dynamiek van een voorraadsysteem.

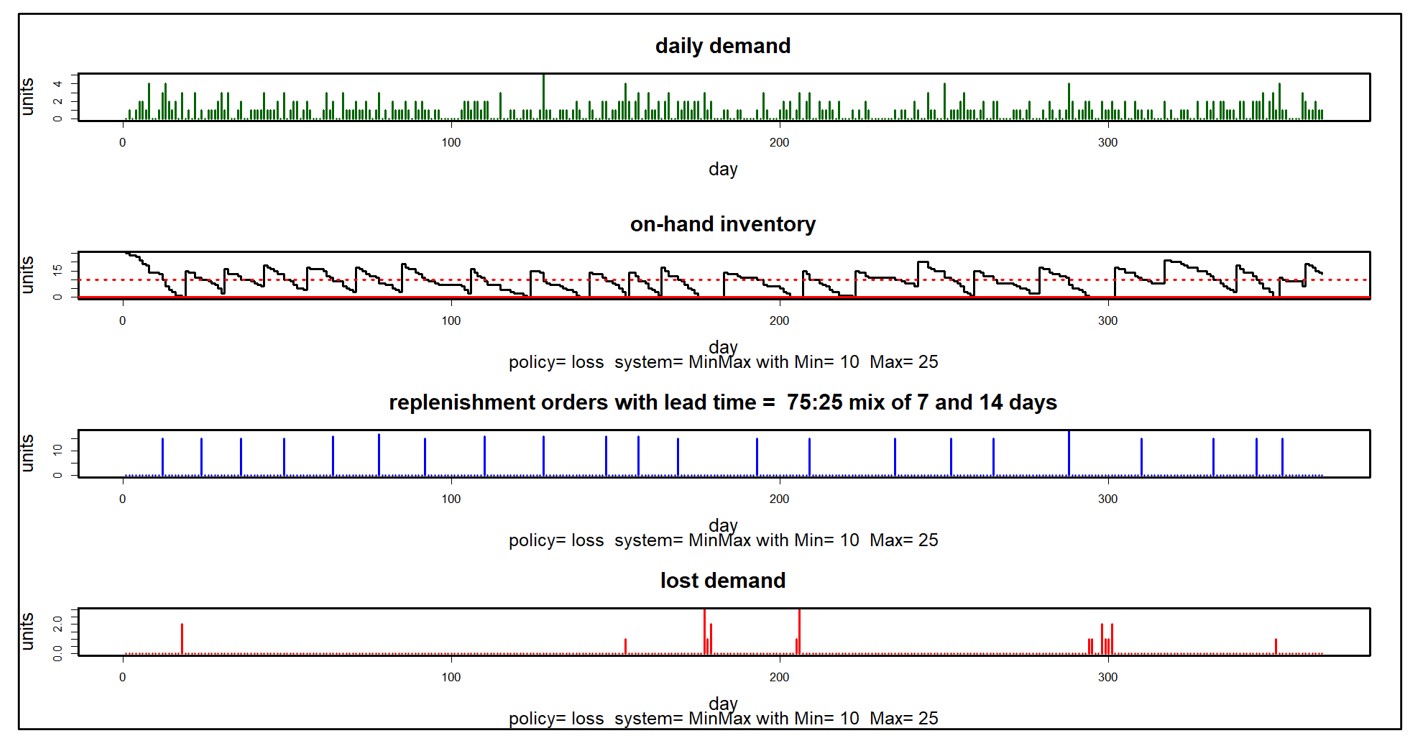
Figuur 2: Details van een Monte Carlo-simulatie

Figuur 2 toont slechts een van de talloze manieren waarop het jaar zou kunnen verlopen. Over het algemeen willen we de resultaten van vele gesimuleerde jaren middelen. Niemand zou tenslotte een munt opgooien om te beslissen of het een eerlijke munt was. Figuur 3 laat zien hoe vier key performance metrics (KPI's) van jaar tot jaar variëren voor dit systeem. Sommige statistieken zijn relatief stabiel in simulaties (Fill Rate), maar andere laten meer relatieve variabiliteit zien (Operating Cost = Holding Cost + Ordering Cost + Shortage Cost). Als we de grafieken bekijken, kunnen we schatten dat de keuzes van Min=10, Max=25 leiden tot gemiddelde bedrijfskosten van ongeveer $3.000 per jaar, een opvullingspercentage van ongeveer 90%, een serviceniveau van ongeveer 75% en een gemiddelde aan Hand van ongeveer 10

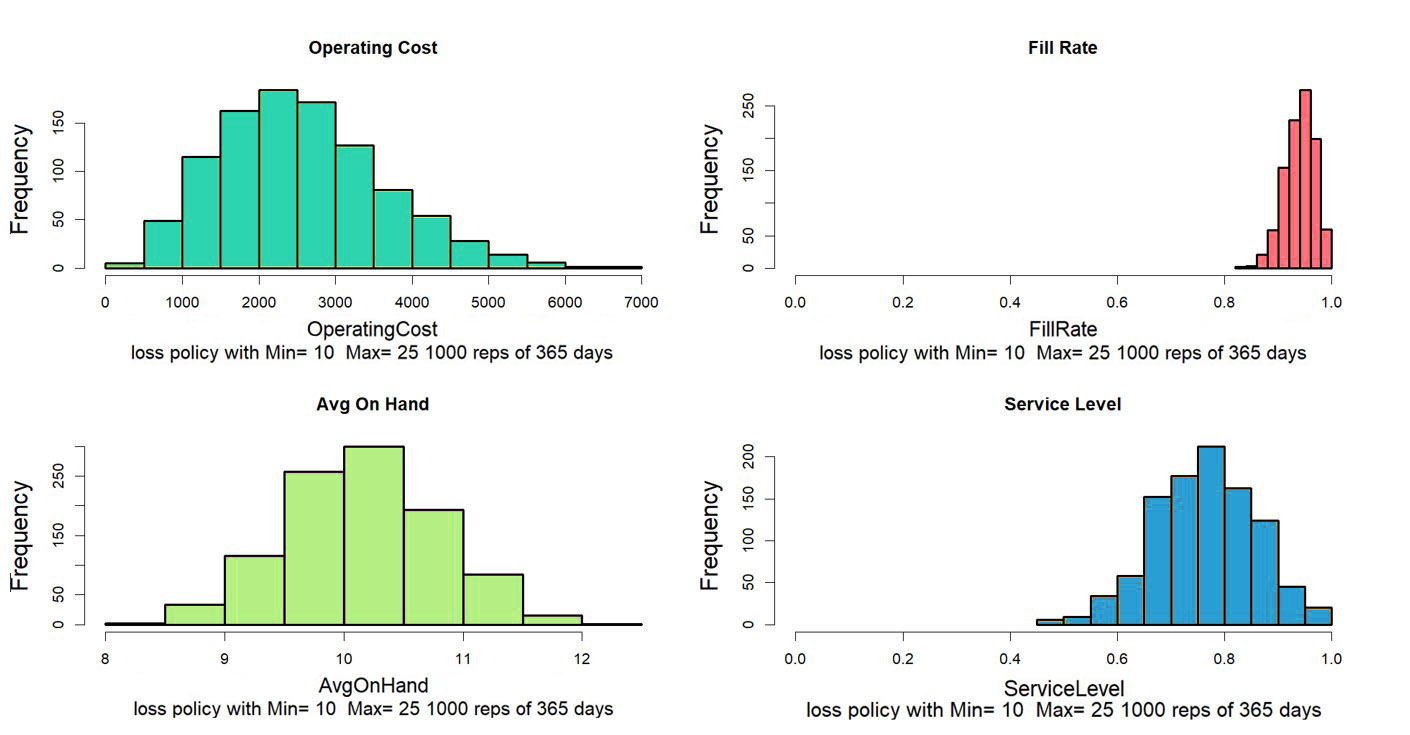
Figuur 3: Variatie in KPI's berekend over 1000 gesimuleerde jaren

Het is nu zelfs mogelijk om een managementvraag van een hoger niveau te beantwoorden. We kunnen verder gaan dan "Wat gebeurt er als ik zus-en-zo doe?" naar “Wat is de best wat ik kan doen om een opvullingspercentage van ten minste 90% voor dit item te bereiken tegen de laagst mogelijke kosten?” De wiskundige  achter deze sprong zit nog een andere sleuteltechnologie genaamd "stochastische optimalisatie", maar we stoppen hier voor nu. Het volstaat te zeggen dat de SIO&P-software van Smart de "ontwerpruimte" van min- en max-waarden kan doorzoeken om automatisch de beste keuze te vinden.

Ontdek hoe prognoses worden gebruikt met deze 4 vragen.

Vaak zullen bedrijven volhouden dat ze "geen prognoses gebruiken" om voorraad te plannen. Ze gebruiken vaak methodes voor bestelpunten en worstelen met het verbeteren van tijdige levering, voorraadrotaties en andere KPI's. Hoewel ze niet denken dat wat ze doen expliciet voorspellen, gebruiken ze zeker schattingen van de toekomstige vraag om bestelpunten zoals min/max te ontwikkelen.

Ongeacht hoe het wordt genoemd, iedereen probeert de toekomstige vraag op de een of andere manier in te schatten en gebruikt deze schatting om voorraadbeleid te bepalen en bestellingen te stimuleren. Om de voorraadplanning te verbeteren en ervoor te zorgen dat u niet te veel of te weinig bestelt en grote voorraden en een opgeblazen gevoel creëert, is het belangrijk om precies te begrijpen hoe uw organisatie prognoses gebruikt. Als dit eenmaal is begrepen, kunt u beoordelen of de kwaliteit van de prognoses kan worden verbeterd.

Probeer antwoorden te krijgen op de volgende vragen. Het zal onthullen hoe prognoses in uw bedrijf worden gebruikt, zelfs als u denkt dat u geen prognoses gebruikt.

1. Is uw prognose een periode-voor-periode schatting in de loop van de tijd die wordt gebruikt om te voorspellen welke voorraad er in de toekomst zal zijn en die bestelsuggesties in uw ERP-systeem activeert?

2. Of wordt uw prognose gebruikt om een bestelpunt af te leiden, maar niet expliciet gebruikt als drijfveer per periode om bestellingen te activeren? Hier kan ik voorspellen dat we er 10 per week zullen verkopen op basis van de geschiedenis, maar we laden niet 10, 10, 10, 10, etc. in het ERP. In plaats daarvan leid ik een bestelpunt of min af dat de doorlooptijd van twee perioden dekt + een hoeveelheid buffer om te helpen beschermen tegen voorraaduitval. In dit geval bestel ik meer wanneer de voorraad op 25 komt.

3. Wordt uw prognose gebruikt als leidraad voor de planner om subjectief te helpen bepalen wanneer ze meer moeten bestellen? Hier voorspel ik er 10 per week, en ik beoordeel de voorhanden inventaris periodiek, bekijk de verwachte doorlooptijd en besluit, gezien de 40 eenheden die ik vandaag bij de hand heb, dat ik "genoeg" heb. Dus ik doe nu niets, maar kom over een week weer terug.

4. Wordt het gebruikt om raamcontracten met leveranciers op te stellen? Hier voorspel ik 10 per week en ga akkoord met een algemene inkooporder met de leverancier van 520 per jaar. De bestellingen worden vervolgens van tevoren geplaatst om eenmaal per week in hoeveelheden van 10 te arriveren totdat de algemene bestelling is verbruikt.

Zodra u de antwoorden heeft, kunt u vragen hoe de schattingen van de vraag tot stand komen. Is het een gemiddelde? Leidt het de vraag over de doorlooptijd af uit een verkoopprognose? Wordt er ergens een statistische prognose gegenereerd? Welke methodes worden overwogen? Het zal ook belangrijk zijn om te beoordelen hoe veiligheidsvoorraden worden gebruikt om te beschermen tegen variabiliteit in vraag en aanbod. Meer over dit alles in een toekomstig artikel.

Als je de laatste tijd je hoofd omhoog hebt gehouden, heb je misschien wat extra waanzin opgemerkt op het basketbalveld: het falen van Silicon Valley Bank. Degenen onder ons in de supply chain-wereld hebben het bankfalen misschien afgedaan als het probleem van iemand anders, maar die spijtige episode bevat ook een grote les voor ons: het belang van stresstesten die goed worden uitgevoerd.

De Washington Post onlangs verscheen een opiniestuk van Natasha Sarin met de titel “Regulators misten de problemen van Silicon Valley Bank maandenlang. Dit is waarom." Sarin schetste de tekortkomingen in het stresstestregime dat de Federal Reserve aan de bank heeft opgelegd. Een probleem is dat de stresstesten te statisch zijn. De stressfactor van de Fed voor de nominale bbp-groei was één enkel scenario met de veronderstelde waarden voor de komende 13 kwartalen (zie figuur 1). Die 13 driemaandelijkse projecties zijn misschien iemands consensus over hoe een bad hair day eruit zou zien, maar dat is niet de enige manier waarop dingen zouden kunnen verlopen. Als samenleving wordt ons geleerd een betere manier te waarderen om onvoorziene omstandigheden weer te geven telkens wanneer de National Weather Service ons geprojecteerde orkaansporen laat zien (zie figuur 2). Elk scenario, weergegeven door een lijn met een andere kleur, toont een mogelijk stormpad, waarbij de geconcentreerde lijnen het meest waarschijnlijke pad vertegenwoordigen. Door de lagere waarschijnlijkheidspaden bloot te leggen, wordt de risicoplanning verbeterd.

Bij het stresstesten van de toeleveringsketen hebben we realistische scenario's nodig van mogelijke toekomstige eisen die zich kunnen voordoen, zelfs extreme eisen. Smart voorziet hierin in onze software (met aanzienlijke verbeteringen in onze Gen2 methodes). De software genereert een groot aantal geloofwaardige vraagscenario's, genoeg om de volledige omvang van de risico's bloot te leggen (zie figuur 3). Stresstesten hebben alles te maken met het genereren van enorme aantallen planningsscenario's, en de probabilistische methoden van Smart wijken radicaal af van eerdere deterministische S&OP-toepassingen, omdat ze volledig op scenario's zijn gebaseerd.

De andere fout in de stresstests van de Fed was dat ze maanden van tevoren waren ontworpen, maar nooit werden bijgewerkt voor veranderende omstandigheden. Vraagplanners en voorraadbeheerders begrijpen intuïtief dat sleutelvariabelen zoals de vraag naar artikelen en de doorlooptijd van leveranciers niet alleen zeer willekeurig zijn, zelfs wanneer de zaken stabiel zijn, maar ook onderhevig zijn aan abrupte verschuivingen die een snelle herschrijving van planningsscenario's vereisen (zie afbeelding 4, waar de gemiddelde vraag springt dramatisch omhoog tussen waarnemingen 19 en 20). Smart's Gen2-producten bevatten nieuwe technologie voor het detecteren van dergelijke "regime verandert' en dienovereenkomstig automatisch veranderende scenario's.

Banken worden gedwongen om stresstests te ondergaan, hoe gebrekkig ze ook mogen zijn, om hun spaarders te beschermen. Supply chain-professionals hebben nu een manier om hun supply chains te beschermen door moderne software te gebruiken om hun vraagplannen en voorraadbeheerbeslissingen aan een stresstest te onderwerpen.

Figuur 1: Scenario's die de Fed gebruikte om banken te stresstesten.

Figuur 2: Scenario's die door de National Weather Service worden gebruikt om orkaansporen te voorspellen

Afbeelding 3: Vraagscenario's van het type gegenereerd door Smart Demand Planner

Figuur 4: Voorbeeld van regimeverandering in productvraag na observatie #19

Of je het nu zelf tot in detail begrijpt of vertrouwt op betrouwbare software, wiskunde is voor iedereen een feit voorraadbeheer en eis voorspelling die hoopt concurrerend te blijven in de moderne wereld.

Op een conferentie onlangs verkondigde de hoofdpresentator in een workshop voorraadbeheer trots dat hij geen behoefte had aan 'hooguitziende wiskunde', waarvan werd uitgelegd dat het iets betekende dat verder ging dan wiskunde van de zesde klas.

Wiskunde is niet ieders eerste liefde. Maar als je er echt om geeft je werk goed te doen, kun je het werk niet benaderen met een basisschoolmentaliteit. Supply chain-taken zoals vraagprognoses en voorraadbeheer zijn dat wel inherent wiskundig. De blog die is gekoppeld aan edX, een vooraanstaande site voor online cursusmateriaal voor hogescholen, heeft een geweldig bericht over dit onderwerp, op https://www.mooc.org/blog/how-is-math-used-in-supply-chain. Ik citeer het eerste stukje:

Wiskunde en de bevoorradingsketen gaan hand in hand. Naarmate toeleveringsketens groeien, zal de toenemende complexiteit bedrijven ertoe aanzetten om manieren te zoeken om grootschalige besluitvorming te beheren. Ze kunnen niet teruggaan naar hoe toeleveringsketens 100 jaar geleden waren – of zelfs twee jaar geleden vóór de pandemie. In plaats daarvan zullen nieuwe technologieën helpen bij het stroomlijnen en beheren van de vele bewegende delen. De logistieke vaardigheden, optimalisatietechnologieën en organisatorische vaardigheden die in de toeleveringsketen worden gebruikt, vereisen allemaal wiskunde.

Onze klanten hoeven geen experts te zijn in supply chain-wiskunde, ze moeten alleen de software kunnen gebruiken die de wiskunde bevat. Software combineert de ervaring van gebruikers en inhoudelijke expertise om resultaten te produceren die het verschil maken tussen succes en falen. Om zijn werk te doen, kan de software niet stoppen bij wiskunde in de zesde klas; het heeft waarschijnlijkheid, statistiek en optimalisatietheorie nodig.

Het is aan ons, softwareleveranciers, om de wiskunde zo te verpakken dat wat er in de berekeningen komt, het enige is dat relevant is, zelfs als het ingewikkeld is; en dat wat eruit komt duidelijk, besluitrelevant en verdedigbaar is wanneer u uw aanbevelingen aan het hoger management moet rechtvaardigen.

Wiskunde van de zesde klas kan u niet waarschuwen wanneer de manier waarop u voorstelt een kritiek reserveonderdeel te beheren, een 70%-kans betekent dat u uw doel voor artikelbeschikbaarheid niet haalt. Het kan u niet vertellen hoe u uw bestelpunten het beste kunt aanpassen wanneer een leverancier belt en zegt: "We hebben een leveringsprobleem." Het kan je huid niet redden als er een verrassend grote bestelling is en je snel moet uitzoeken wat de beste manier is om een aantal versnelde speciale bestellingen op te zetten zonder het operationele budget te vernietigen.

Respecteer dus de volkswijsheid en neem geen mes mee naar een vuurgevecht.