Het meten van de nauwkeurigheid van prognoses is een onmiskenbaar belangrijk onderdeel van het vraagplanningsproces. Deze voorspellingsscorekaart zou kunnen worden opgebouwd op basis van een van de twee contrasterende gezichtspunten voor het berekenen van metrieken. Vanuit het foutperspectief wordt de vraag gesteld: “Hoe ver lag de voorspelling van de werkelijkheid?” Vanuit het nauwkeurigheidsperspectief wordt de vraag gesteld: “Hoe dicht lag de voorspelling bij de werkelijkheid?” Beide zijn geldig, maar foutstatistieken bieden meer informatie.

Nauwkeurigheid wordt weergegeven als een percentage tussen nul en 100, terwijl foutpercentages bij nul beginnen maar geen bovengrens hebben. Rapporten van MAPE (gemiddelde absolute procentuele fout) of andere foutstatistieken kunnen de titel 'voorspellingsnauwkeurigheid'-rapporten krijgen, waardoor het onderscheid vervaagt. Het kan dus zijn dat u wilt weten hoe u vanuit het foutenperspectief kunt overstappen naar het nauwkeurigheidsperspectief dat uw bedrijf omarmt. In deze blog wordt aan de hand van enkele voorbeelden beschreven hoe.

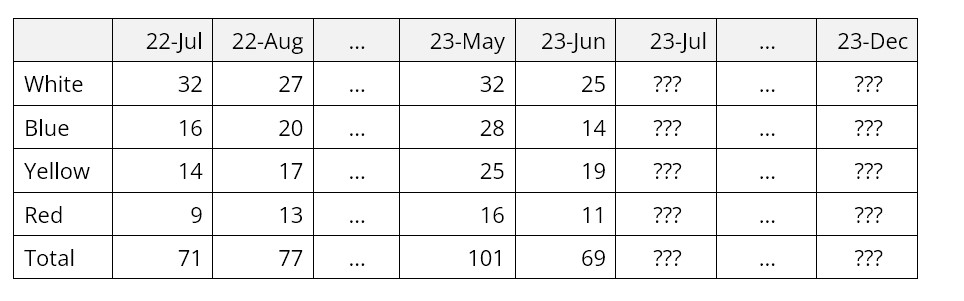
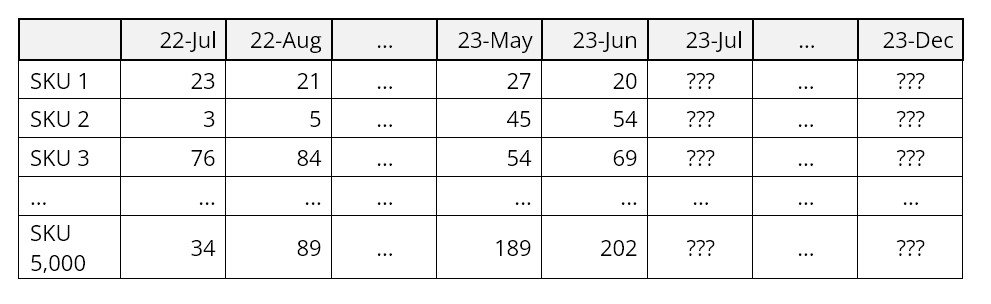
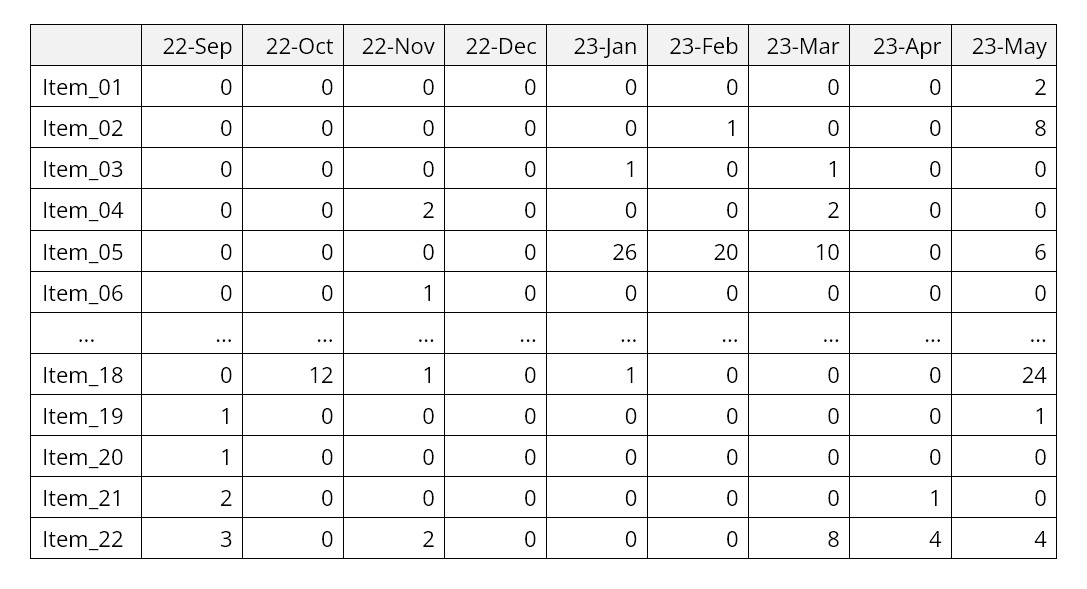
Nauwkeurigheidsgegevens worden zo berekend dat wanneer de werkelijke waarde gelijk is aan de voorspelling, de nauwkeurigheid 100% is en wanneer de voorspelling het dubbele of de helft is van de werkelijke, de nauwkeurigheid 0% is. Rapporten waarin de voorspelling met de werkelijkheid wordt vergeleken, bevatten vaak het volgende:

• De daadwerkelijke
• De prognose
• Eenheidsfout = Prognose – Werkelijk
• Absolute fout = Absolute waarde van eenheidsfout
• Absolute %-fout = Abs-fout / Werkelijk, als een %
• Nauwkeurigheid % = 100% – Absolute %-fout

Bekijk een paar voorbeelden die het verschil in aanpak illustreren. Stel dat de Werkelijke = 8 en de voorspelling is 10.

Eenheidsfout is 10 – 8 = 2

Absolute %-fout = 2/8, als % = 0,25 * 100 = 25%

Nauwkeurigheid = 100% – 25% = 75%.

Laten we nu zeggen dat de werkelijke waarde 8 is en de voorspelling 24.

Eenheidsfout is 24– 8 = 16

Absolute %-fout = 16/8 als % = 2 * 100 = 200%

Nauwkeurigheid = 100% – 200% = negatief is ingesteld op 0%.

In het eerste voorbeeld leveren nauwkeurigheidsmetingen dezelfde informatie op als foutmetingen, aangezien de voorspelling en de werkelijke situatie al relatief dicht bij elkaar liggen. Maar als de fout meer dan het dubbele is van de werkelijke, komen de nauwkeurigheidsmetingen uit op nul. Het geeft wel correct aan dat de voorspelling helemaal niet accuraat was. Maar het tweede voorbeeld is nauwkeuriger dan een derde, waarbij de werkelijke waarde 8 is en de voorspelling 200. Dat is een onderscheid dat een nauwkeurigheidsbereik van 0 tot 100% niet registreert. In dit laatste voorbeeld:

Eenheidsfout is 200 – 8 = 192

Absolute %-fout = 192/8, als % = 24 * 100 = 2,400%

Nauwkeurigheid = 100% – 2.400% = negatief is ingesteld op 0%.

Foutstatistieken blijven informatie verschaffen over hoe ver de voorspelling afwijkt van de werkelijke en geven aantoonbaar een betere weergave van de nauwkeurigheid van de voorspelling.

Wij moedigen aan om het foutperspectief te hanteren. U hoopt eenvoudigweg op een klein foutpercentage dat aangeeft dat de voorspelling niet ver van de werkelijkheid ligt, in plaats van te hopen op een groot nauwkeurigheidspercentage dat aangeeft dat de voorspelling dicht bij de werkelijkheid ligt. Deze mentaliteitsverandering biedt dezelfde inzichten en elimineert vervormingen.

Automatische prognoses zijn de populairste en meest gebruikte functie van SmartForecasts en Smart Demand Planner. Automatische prognoses maken is eenvoudig. Maar de eenvoud van Automatic Forecasting maskeert een krachtige interactie van een aantal zeer effectieve prognosemethoden. In deze blog bespreken we een deel van de theorie achter deze kernfunctie. We richten ons op automatische prognoses, deels vanwege de populariteit ervan en deels omdat veel andere prognosemethoden vergelijkbare resultaten opleveren. Kennis van automatische prognoses wordt onmiddellijk overgedragen naar eenvoudig voortschrijdend gemiddelde, lineair voortschrijdend gemiddelde, enkele exponentiële afvlakking, dubbele exponentiële afvlakking, Winters' exponentiële afvlakking en promoprognoses.

Prognose toernooi

Automatische prognoses werken door een toernooi uit te voeren met een reeks concurrerende methoden. Omdat personal computers en cloud computing snel zijn, en omdat we zeer efficiënte algoritmen hebben gecodeerd in de automatische voorspellingsengine van SmartForecasts, is het praktisch om een puur empirische benadering te volgen om te beslissen welke extrapolatieve voorspellingsmethode moet worden gebruikt. Dit betekent dat u het zich kunt veroorloven om een aantal benaderingen uit te proberen en vervolgens degene te behouden die het beste presteert bij het voorspellen van de betreffende gegevensreeks. SmartForecasts automatiseert dit proces volledig voor u door de verschillende voorspellingsmethoden uit te proberen in een gesimuleerd voorspellingstoernooi. De winnaar van het toernooi is de methode die het dichtst bij het voorspellen van nieuwe gegevenswaarden van oude komt. Nauwkeurigheid wordt gemeten aan de hand van de gemiddelde absolute fout (dat wil zeggen de gemiddelde fout, waarbij eventuele mintekens worden genegeerd). Het gemiddelde wordt berekend over een reeks voorspellingen, die elk een deel van de gegevens gebruiken, in een proces dat bekend staat als glijdende simulatie.

Glijdende simulatie

De glijdende simulatie veegt herhaaldelijk door steeds langere delen van de historische gegevens, waarbij in elk geval het gewenste aantal perioden in uw prognosehorizon wordt voorspeld. Stel dat er 36 historische gegevenswaarden zijn en dat u zes perioden vooruit moet voorspellen. Stel je voor dat je de voorspellingsnauwkeurigheid van een bepaalde methode, bijvoorbeeld een voortschrijdend gemiddelde van vier waarnemingen, wilt beoordelen op de gegevensreeks die voorhanden is.

Op een gegeven moment in de glijdende simulatie worden de eerste 24 punten (alleen) gebruikt om de 25e tot en met 30e historische gegevenswaarden te voorspellen, die we tijdelijk als onbekend beschouwen. We zeggen dat de punten 25-30 buiten de analyse worden gehouden. Het berekenen van de absolute waarden van de verschillen tussen de zes prognoses en de overeenkomstige werkelijke historische waarden levert één exemplaar op van elk een 1-staps, 2-staps, 3-staps, 4-staps, 5-staps en 6-staps vooruit absolute voorspelling fout. Als u dit proces herhaalt met de eerste 25 punten, krijgt u meer voorbeelden van 1-staps, 2-staps, 3-staps vooruit-fouten, enzovoort. Het gemiddelde van alle absolute foutschattingen die op deze manier zijn verkregen, geeft een samenvatting van de nauwkeurigheid in één getal.

Methoden die worden gebruikt bij automatische prognoses

Normaal gesproken zijn er zes extrapolatieve voorspellingsmethoden die meedoen aan het automatische voorspellingstoernooi:

• Eenvoudig voortschrijdend gemiddelde
• Lineair voortschrijdend gemiddelde
• Enkele exponentiële afvlakking
• Dubbele exponentiële afvlakking
• Additieve versie van Winters' exponentiële afvlakking
• Multiplicatieve versie van Winters' exponentiële afvlakking

De laatste twee methoden zijn geschikt voor seizoenreeksen; ze worden echter automatisch uitgesloten van het toernooi als er minder dan twee volledige seizoensgegevenscycli zijn (bijvoorbeeld minder dan 24 periodes met maandelijkse gegevens of acht periodes met driemaandelijkse gegevens).

Deze zes klassieke, op afvlakking gebaseerde methoden hebben bewezen gemakkelijk te begrijpen, gemakkelijk te berekenen en nauwkeurig te zijn. Je kunt elk van deze methoden uitsluiten van het toernooi als je een voorkeur hebt voor sommige deelnemers en niet voor andere.

1. Voorspellen is een kunst die een combinatie van professioneel oordeel en objectieve statistische analyse vereist. Succesvolle vraagprognoses vereisen een basisvoorspelling die gebruikmaakt van statistische prognosemethoden. Eenmaal vastgesteld, kan het proces zich richten op hoe u statistische prognoses het beste kunt aanpassen op basis van uw eigen inzichten en zakelijke kennis.

2. Het prognoseproces is meestal iteratief. Het kan zijn dat u uw aanvankelijke prognose een aantal keer moet verfijnen voordat u tevreden bent. Het is belangrijk om snel en eenvoudig alternatieve prognoses te kunnen genereren en vergelijken. Het volgen van de nauwkeurigheid van deze prognoses in de loop van de tijd, inclusief alternatieven die niet werden gebruikt, helpt het proces te informeren en te verbeteren.

3. De geloofwaardigheid van prognoses hangt sterk af van grafische vergelijkingen met historische gegevens. Een beeld zegt meer dan duizend woorden, dus geef prognoses altijd weer via direct beschikbare grafische displays met ondersteunende numerieke rapporten.

4. Een van de belangrijkste technische taken bij prognoses is om de keuze van de prognosetechniek af te stemmen op de aard van de gegevens. Effectieve vraagvoorspellingsprocessen maken gebruik van mogelijkheden die de juiste methode identificeren om te gebruiken. Kenmerken van een datareeks zoals trend, seizoensinvloeden of abrupte niveauverschuivingen suggereren bepaalde technieken in plaats van andere. Een automatische selectie, die automatisch de juiste prognosemethode selecteert en gebruikt, bespaart tijd en zorgt ervoor dat uw basisvoorspelling zo nauwkeurig mogelijk is.

5. Succesvolle vraagvoorspellingsprocessen werken samen met andere bedrijfsprocessen. Prognoses kunnen bijvoorbeeld een essentiële eerste stap zijn in financiële analyse. Bovendien zijn nauwkeurige prognoses voor verkoop en productvraag fundamentele input voor de processen voor productieplanning en voorraadbeheer van een productiebedrijf.

6. Een goed planningsproces erkent dat prognoses nooit precies kloppen. Omdat zelfs in het beste prognoseproces een fout sluipt, zijn eerlijke schattingen van de foutmarge en prognosebias een van de nuttigste aanvullingen op een prognose.

Veel bedrijven die hun prognoseproces willen verbeteren, weten niet waar ze moeten beginnen. Het kan verwarrend zijn om te worstelen met het leren van nieuwe statistische methoden, ervoor zorgen dat gegevens correct zijn gestructureerd en bijgewerkt, het eens worden over wie "eigenaar" is van de prognose, definiëren wat eigendom betekent en meetnauwkeurigheid. Na meer dan veertig jaar oefenen hebben we deze blog geschreven om de belangrijkste focus te schetsen en om u aan te moedigen om het in het begin simpel te houden.

1. Objectiviteit. Begrijp en communiceer eerst dat het proces van vraagplanning en -prognose een oefening in objectiviteit is. De focus ligt op het verkrijgen van input uit verschillende bronnen (stakeholders, klanten, functioneel beheerders, databases, leveranciers, enz.) en het bepalen of die input waarde toevoegt. Als u bijvoorbeeld een statistische prognose overschrijft en 20% aan de projectie toevoegt, moet u er niet zomaar van uitgaan dat u het automatisch goed had. Wees in plaats daarvan objectief en controleer of die opheffing de prognosenauwkeurigheid heeft vergroot of verkleind. Als u merkt dat uw overrides de zaken erger hebben gemaakt, heeft u iets gewonnen: dit informeert het proces en u weet dat u in de toekomst override-beslissingen beter kunt onderzoeken.

2. Teamwerk. Erken dat prognoses en vraagplanning teamsporten zijn. Maak afspraken over wie het team zal aanvoeren. De kapitein is verantwoordelijk voor het maken van de statistische basisprognoses en het toezicht houden op het vraagplanningsproces. Maar de resultaten zijn afhankelijk van het feit of iedereen in het team een positieve bijdrage levert, gegevens verstrekt, alternatieve methoden voorstelt, aannames in twijfel trekt en aanbevolen acties uitvoert. De uiteindelijke resultaten zijn eigendom van het bedrijf en elke afzonderlijke belanghebbende.

3. Meting. Fixeer u niet op benchmarks voor de nauwkeurigheid van prognoses in de branche. Elke SKU heeft zijn eigen niveau van "voorspelbaarheid", en u kunt een aantal moeilijke items beheren. Creëer in plaats daarvan uw eigen benchmarks op basis van een reeks steeds geavanceerdere prognosemethoden. Geavanceerde statistische prognoses lijken in het begin misschien ontmoedigend ingewikkeld, dus begin eenvoudig met een basismethode, zoals het voorspellen van de historische gemiddelde vraag. Meet vervolgens hoe dicht die simpele voorspelling de werkelijk waargenomen vraag benadert. Werk van daaruit verder naar technieken die te maken hebben met complicaties zoals trend en seizoensinvloeden. Meet de voortgang met behulp van nauwkeurigheidsstatistieken die door uw software zijn berekend, zoals de gemiddelde absolute procentuele fout (MAPE). Hierdoor kan uw bedrijf elke prognosecyclus een beetje beter worden.

4. Tempo. Richt u vervolgens op het maken van prognoses tot een op zichzelf staand proces dat niet wordt gecombineerd met het complexe proces van voorraadoptimalisatie. Voorraadbeheer is gebaseerd op een solide vraagvoorspelling, maar is gericht op andere onderwerpen: wat te kopen, wanneer te kopen, minimale bestelhoeveelheden, veiligheidsvoorraden, voorraadniveaus, doorlooptijden van leveranciers, enz. Laat voorraadbeheer later verder gaan . Bouw eerst "voorspellingskracht" op door het voorspellingsproces te creëren, te herzien en te ontwikkelen om een regelmatige cadans te hebben. Wanneer uw proces voldoende volwassen is, kunt u de toenemende snelheid van het bedrijfsleven bijbenen door het tempo van uw prognoseproces te verhogen tot ten minste een maandelijks tempo.

Opmerkingen

Het herzien van het prognoseproces van een bedrijf kan een grote stap zijn. Soms gebeurt het als er personeelsverloop is, soms als er een nieuw ERP-systeem is, soms als er nieuwe prognosesoftware is. Wat de overhaaste gebeurtenis ook is, deze verandering is een kans om het proces dat je eerder had te heroverwegen en te verfijnen. Maar proberen de hele olifant in één keer op te eten is een vergissing. In deze blog hebben we enkele discrete stappen uiteengezet die u kunt nemen om een succesvolle evolutie naar een beter prognoseproces te maken.

Hier zijn voorbeelden van prognoseproblemen die SmartForecasts kan oplossen, samen met de soorten bedrijfsgegevens die representatief zijn voor elk.

Een item voorspellen op basis van het patroon

Welke omzet kunt u, gegeven de volgende zes kwartaalverkoopcijfers, verwachten voor het derde en vierde kwartaal van 2023?

Verkoop per kwartaal

SmartForecasts biedt u vele manieren om dit probleem aan te pakken. U kunt uw eigen statistische prognoses maken met een van de zes verschillende Exponential smoothing en Moving average methoden. Of, zoals de meeste niet-technische voorspellers, kunt u de tijdbesparende automatische opdracht gebruiken, die is geprogrammeerd om automatisch de meest nauwkeurige methode voor uw gegevens te selecteren en te gebruiken. Ten slotte kunt u, om uw zakelijke oordeel in het prognoseproces op te nemen, elk statistisch prognoseresultaat grafisch aanpassen met behulp van SmartForecasts' "oogbol" aanpassing mogelijkheden.

Een item voorspellen op basis van zijn relatie met andere variabelen.

Gezien de volgende historische relatie tussen de verkoop per eenheid en het aantal vertegenwoordigers, welke verkoopniveaus kunt u verwachten wanneer de geplande toename van het verkooppersoneel plaatsvindt in de laatste twee kwartalen van 2023?

Verkoop en verkoopvertegenwoordigers per kwartaal

U kunt een vraag als deze beantwoorden met behulp van het krachtige SmartForecasts Regressie commando, speciaal ontworpen om prognosetoepassingen te vergemakkelijken die oplossingen voor regressieanalyse vereisen. Regressiemodellen met een vrijwel onbeperkt aantal onafhankelijke/voorspellersvariabelen zijn mogelijk, hoewel de meeste bruikbare regressiemodellen slechts een handvol voorspellers gebruiken.

Gelijktijdig een aantal productitems en hun totaal voorspellen

Gegeven de volgende totale verkoop voor alle overhemden en de verdeling van de verkoop per kleur, wat zal de individuele en totale verkoop zijn in de komende zes maanden?

Maandelijkse verkoop van overhemden per kleur

De unieke Group Forecasting-functies van SmartForecasts voorspellen automatisch en gelijktijdig nauw verwante tijdreeksen, zoals deze artikelen in dezelfde productgroep. Dit bespaart veel tijd en levert prognoseresultaten op, niet alleen voor de afzonderlijke artikelen, maar ook voor het totaal. "Eyeball"-aanpassingen op zowel item- als groepsniveau zijn eenvoudig te maken. U kunt snel prognoses maken voor productgroepen met honderden of zelfs duizenden artikelen.

Automatisch duizenden items voorspellen

Wat kunt u verwachten van de vraag in de komende zes maanden voor elk van de 5.000 SKU's, gegeven het volgende record van productvraag op SKU-niveau?

Maandelijkse productvraag per SKU (Stock Keeping Unit)

In slechts een paar minuten kan de krachtige automatische selectie van SmartForecasts een prognosetaak van deze omvang uitvoeren, de gegevens over de productvraag lezen, automatisch statistische prognoses voor elke SKU maken en het resultaat opslaan. De resultaten zijn vervolgens klaar voor export naar uw ERP-systeem met behulp van een van onze API-gebaseerde connectoren of via bestandsexport. Eenmaal ingesteld, worden er automatisch elke planningscyclus prognoses gemaakt zonder tussenkomst van de gebruiker.

Voorspelling van de vraag die meestal nul is

Een apart en vooral uitdagend type data om te voorspellen is periodieke vraag, die meestal nul is, maar op willekeurige tijdstippen omhoog springt naar willekeurige waarden die niet gelijk zijn aan nul. Dit patroon is typerend voor de vraag naar langzaam in beweging items, zoals service-onderdelen of groot ticket kapitaalgoederen.

Kijk bijvoorbeeld eens naar het volgende voorbeeld van de vraag naar serviceonderdelen voor vliegtuigen. Let op het overwicht van nulwaarden met niet-nulwaarden vermengd, vaak in bursts.

SmartForecasts heeft een unieke methode die speciaal is ontworpen voor dit soort data: de functie Intermittent Demand forecasting. Aangezien intermitterende vraag het vaakst ontstaat in de context van voorraadbeheer, richt deze functie zich op het voorspellen van het bereik van waarschijnlijke waarden voor de totale vraag gedurende een doorlooptijd, bijvoorbeeld de cumulatieve vraag over de periode van 23 juni tot 23 augustus in het bovenstaande voorbeeld .

Voorspellen van voorraadbehoeften

Het voorspellen van voorraadvereisten is een gespecialiseerde variant van prognoses die zich richt op de bovenkant van het bereik van mogelijke toekomstige waarden.

Overweeg voor de eenvoud het probleem van het voorspellen van voorraadbehoeften voor slechts één periode vooruit, bijvoorbeeld één dag vooruit. Gewoonlijk is de prognosetaak het schatten van het meest waarschijnlijke of gemiddelde niveau van de productvraag. Als de beschikbare voorraad echter gelijk is aan de gemiddelde vraag, is er een kans van ongeveer 50% dat de vraag de voorraad overtreft, wat resulteert in omzetverlies en/of goodwill. Het voorraadniveau instellen op bijvoorbeeld tien keer de gemiddelde vraag zal waarschijnlijk het probleem van stockouts elimineren, maar zal net zo zeker resulteren in opgeblazen voorraadkosten.

De truc van voorraadoptimalisatie is om een bevredigende balans te vinden tussen voldoende voorraad hebben om aan de meeste vraag te voldoen zonder al te veel middelen in het proces vast te leggen. Meestal is de oplossing een combinatie van zakelijk inzicht en statistieken. Het beoordelende deel is het definiëren van een acceptabel voorraadserviceniveau, zoals het direct uit voorraad voldoen aan 95% vraag. Het statistische deel is om het 95e percentiel van de vraag te schatten.

Wanneer niet omgaan met Intermittent demand, schat SmartForecasts het vereiste voorraadniveau door uit te gaan van een klokvormige (normale) vraagcurve, zowel het midden als de breedte van de klokcurve te schatten en vervolgens een standaard statistische formule te gebruiken om het gewenste percentiel te schatten. Het verschil tussen het gewenste voorraadniveau en het gemiddelde niveau van de vraag wordt de veiligheidsvoorraad genoemd omdat het beschermt tegen de mogelijkheid van stockouts.

Bij intermitterende vraag is de klokvormige curve een slechte benadering van de statistische verdeling van de vraag. In dit speciale geval gebruikt SmartForecasts gepatenteerde intermitterende vraagvoorspellingstechnologie om het vereiste voorraadserviceniveau te schatten.