Wat is er anders aan voorraadplanning voor onderhoud, reparatie en bewerkingen (MRO) vergeleken met voorraadplanning in productie- en distributieomgevingen? Kortom, het is de aard van de vraagpatronen in combinatie met het gebrek aan bruikbare bedrijfskennis.

Vraagpatronen

Fabrikanten en distributeurs hebben de neiging zich te concentreren op de topverkopers die het grootste deel van hun omzet genereren. Er is doorgaans een grote vraag naar deze artikelen, die relatief eenvoudig te voorspellen zijn met traditionele tijdreeksmodellen die inspelen op voorspelbare trends en/of seizoensinvloeden. Daarentegen hebben MRO-planners bijna altijd te maken met een intermitterende vraag, die schaarser, willekeuriger en moeilijker te voorspellen is. Bovendien zijn de fundamentele hoeveelheden van belang verschillend. MRO-planners geven uiteindelijk het meeste om de ‘wanneer’-vraag: wanneer gaat er iets kapot? Terwijl de anderen zich concentreren op de “hoeveel” vraag van verkochte eenheden.

Zakelijke kennis

Productie- en distributieplanners kunnen vaak rekenen op het verzamelen van klant- en verkoopfeedback, die kan worden gecombineerd met statistische methoden om de nauwkeurigheid van de prognoses te verbeteren. Aan de andere kant zijn lagers, tandwielen, verbruiksartikelen en repareerbare onderdelen zelden bereid hun mening te delen. Met MRO is bedrijfskennis over welke onderdelen nodig zijn en wanneer niet betrouwbaar (behalve gepland onderhoud wanneer verbruiksartikelen in grotere volumes worden vervangen). Het succes van de MRO-voorraadplanning gaat dus slechts zo ver als het vermogen van hun waarschijnlijkheidsmodellen om toekomstig gebruik te voorspellen. En omdat de vraag zo wisselend is, kunnen ze met traditionele benaderingen niet voorbij Go komen.

Methoden voor MRO

In de praktijk is het gebruikelijk dat MRO- en activa-intensieve bedrijven hun voorraden beheren door hun toevlucht te nemen tot statische Min/Max-niveaus op basis van subjectieve veelvouden van gemiddeld gebruik, aangevuld met incidentele handmatige aanpassingen op basis van onderbuikgevoelens. Het proces wordt een slechte mix van statisch en reactief, met als resultaat dat er veel tijd en geld wordt verspild aan het versnellen.

Er zijn alternatieve planningsmethoden die meer op wiskunde en data zijn gebaseerd, hoewel deze stijl van plannen bij MRO minder gebruikelijk is dan in de andere domeinen. Er zijn twee toonaangevende benaderingen voor het modelleren van defecten aan onderdelen en machines: modellen gebaseerd op de betrouwbaarheidstheorie en modellen voor ‘conditiegebaseerd onderhoud’ gebaseerd op realtime monitoring.

Betrouwbaarheidsmodellen

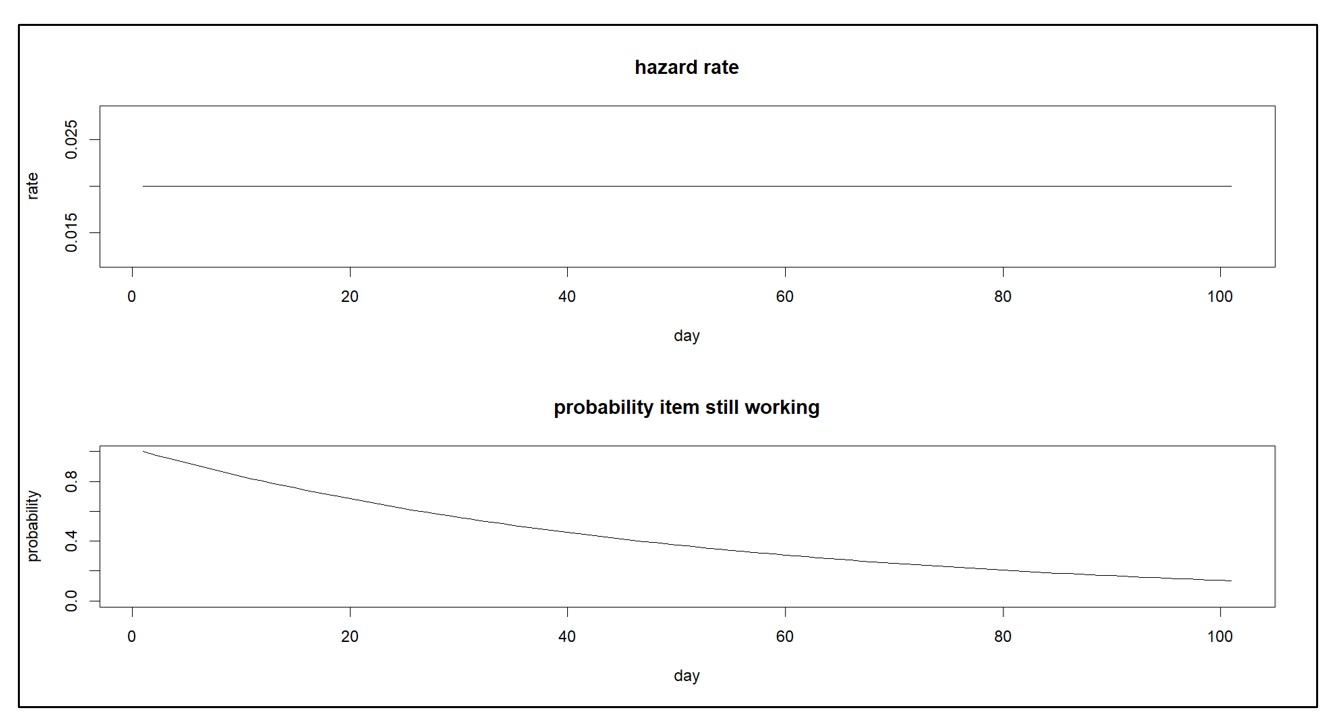
Betrouwbaarheidsmodellen zijn de eenvoudigste van de twee en vereisen minder gegevens. Ze gaan ervan uit dat alle artikelen van hetzelfde type, bijvoorbeeld een bepaald reserveonderdeel, statistisch gelijkwaardig zijn. Hun belangrijkste onderdeel is een ‘gevarenfunctie’, die het risico op falen in het volgende korte tijdsinterval beschrijft. De gevarenfunctie kan worden vertaald in iets dat beter geschikt is voor besluitvorming: de ‘overlevingsfunctie’, wat de waarschijnlijkheid is dat het item nog steeds werkt na X gebruiksduur (waarbij X kan worden uitgedrukt in dagen, maanden, kilometers, gebruik, enz.). Figuur 1 toont een constante gevaarfunctie en de bijbehorende overlevingsfunctie.

Figuur 1: Constante gevarenfunctie en zijn overlevingsfunctie

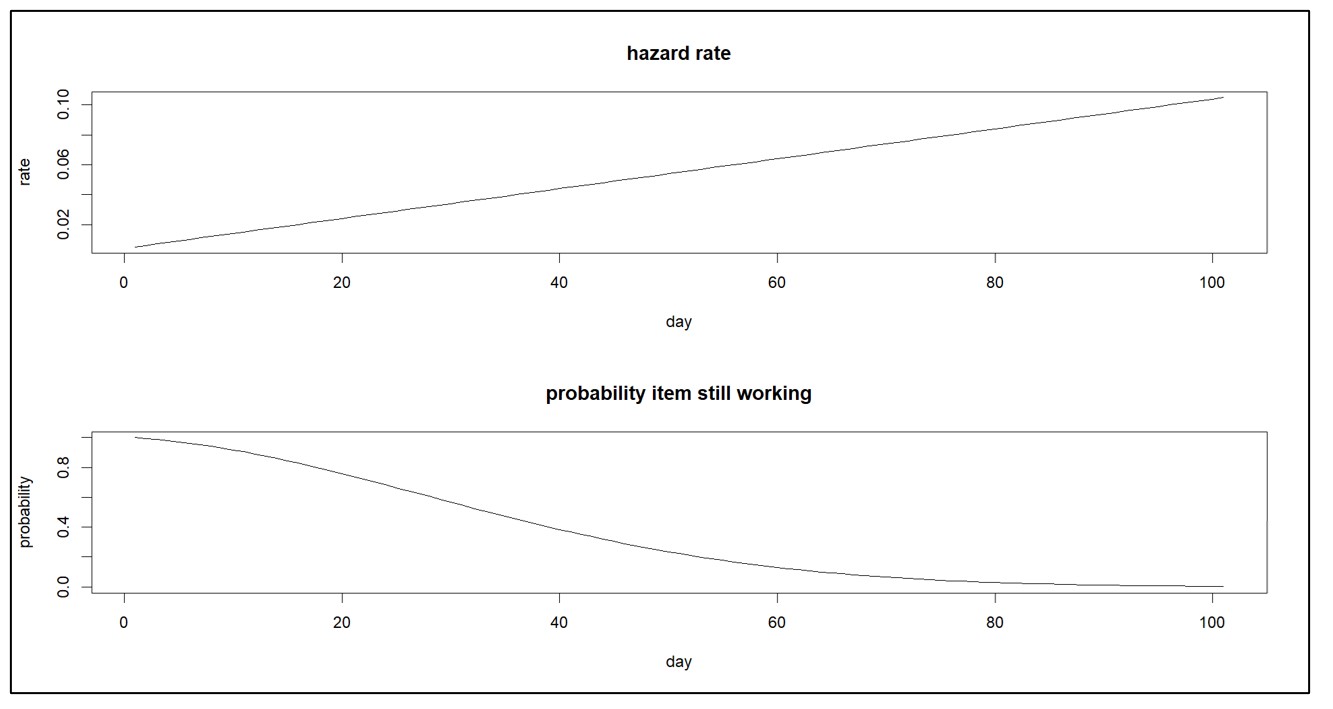
Een gevarenfunctie die niet verandert, houdt in dat alleen willekeurige ongelukken een storing veroorzaken. Een gevaarfunctie die in de loop van de tijd toeneemt, impliceert daarentegen dat het artikel versleten is. En een afnemende gevaarfunctie impliceert dat een item zich vestigt. Figuur 2 toont een toenemende gevaarfunctie en de bijbehorende overlevingsfunctie.

Figuur 2: Toenemende gevarenfunctie en zijn overlevingsfunctie

Betrouwbaarheidsmodellen worden vaak gebruikt voor goedkope onderdelen, zoals mechanische bevestigingsmiddelen, waarvan de vervanging misschien niet moeilijk of duur is (maar toch essentieel kan zijn).

Conditiegebaseerd onderhoud

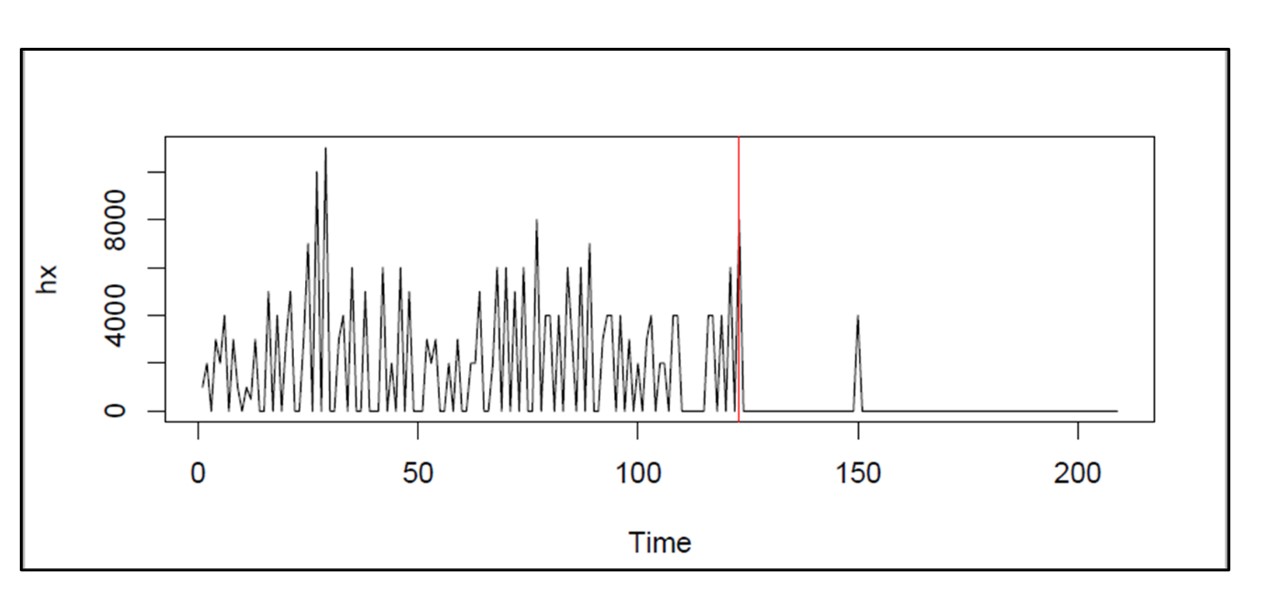
Modellen gebaseerd op real-time monitoring worden gebruikt ter ondersteuning van condition-based onderhoud (CBM) voor dure zaken als straalmotoren. Deze modellen gebruiken gegevens van sensoren die in de items zelf zijn ingebed. Dergelijke gegevens zijn doorgaans complex en bedrijfseigen, evenals de waarschijnlijkheidsmodellen die door de gegevens worden ondersteund. Het voordeel van real-time monitoring is dat je problemen kunt zien aankomen, dat wil zeggen dat de verslechtering zichtbaar wordt gemaakt en dat voorspellingen kunnen voorspellen wanneer het item de rode lijn zal bereiken en daarom uit het speelveld moet worden gehaald. Dit maakt geïndividualiseerd, proactief onderhoud of vervanging van het artikel mogelijk.

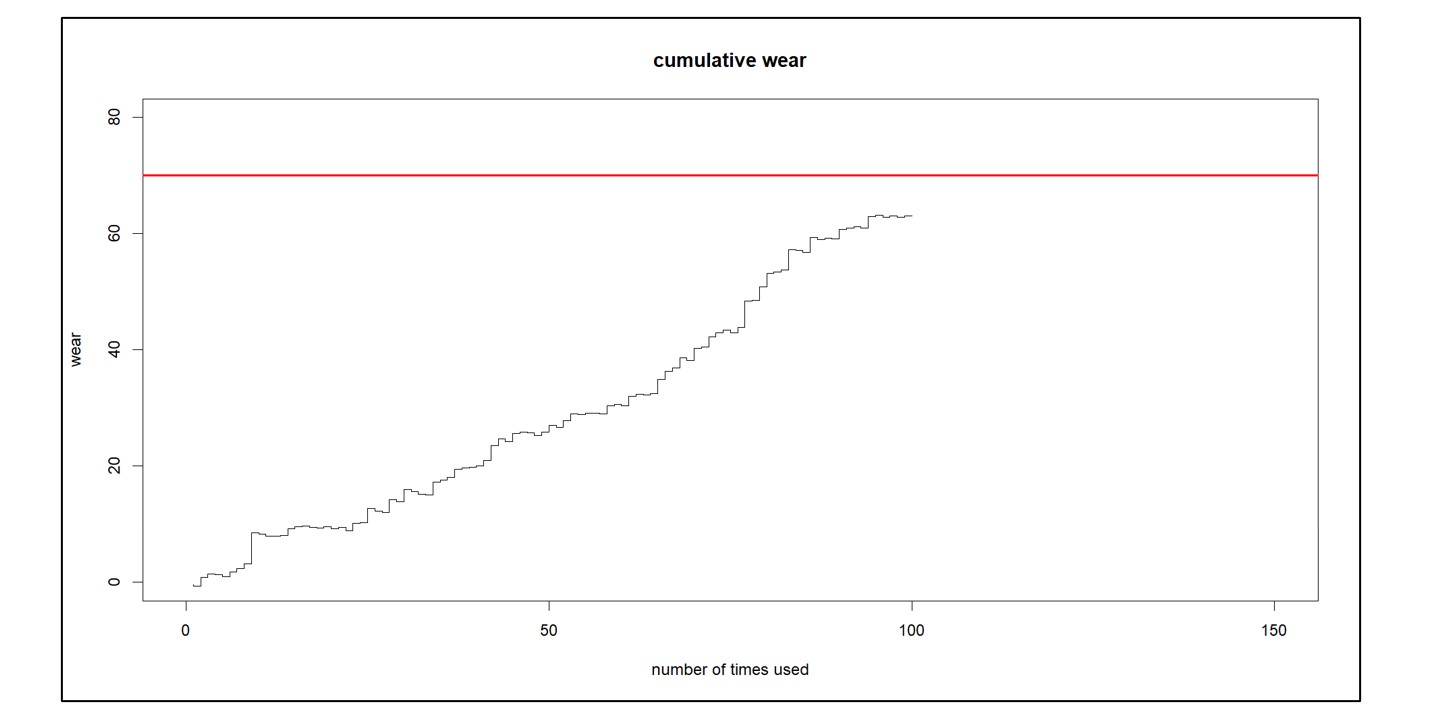
Figuur 3 illustreert het soort gegevens dat in CBM wordt gebruikt. Elke keer dat het systeem wordt gebruikt, is er een bijdrage aan de cumulatieve slijtage ervan. (Houd er echter rekening mee dat gebruik soms de staat van het apparaat kan verbeteren, bijvoorbeeld wanneer regen een machine koel houdt). U kunt de algemene trend naar boven zien richting een rode lijn, waarna het apparaat onderhoud nodig heeft. U kunt de cumulatieve slijtage extrapoleren om in te schatten wanneer deze de rode lijn zal bereiken en dienovereenkomstig plannen.

Figuur 3: Ter illustratie van real-time monitoring voor conditiegebaseerd onderhoud

Voor zover ik weet, maakt niemand zulke modellen van klanten met eindproducten om te voorspellen wanneer en hoeveel ze de volgende keer zullen bestellen, misschien omdat de klanten er bezwaar tegen zouden hebben om voortdurend hersenmonitors te dragen. Maar CBM, met zijn complexe monitoring en modellering, wint aan populariteit voor systemen die niet kunnen falen, zoals straalmotoren. Ondertussen hebben klassieke betrouwbaarheidsmodellen nog steeds veel waarde voor het beheer van grote vloten met goedkopere maar nog steeds essentiële artikelen.

Smart's aanpak
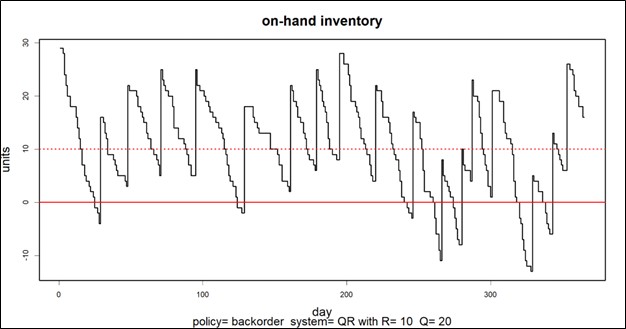
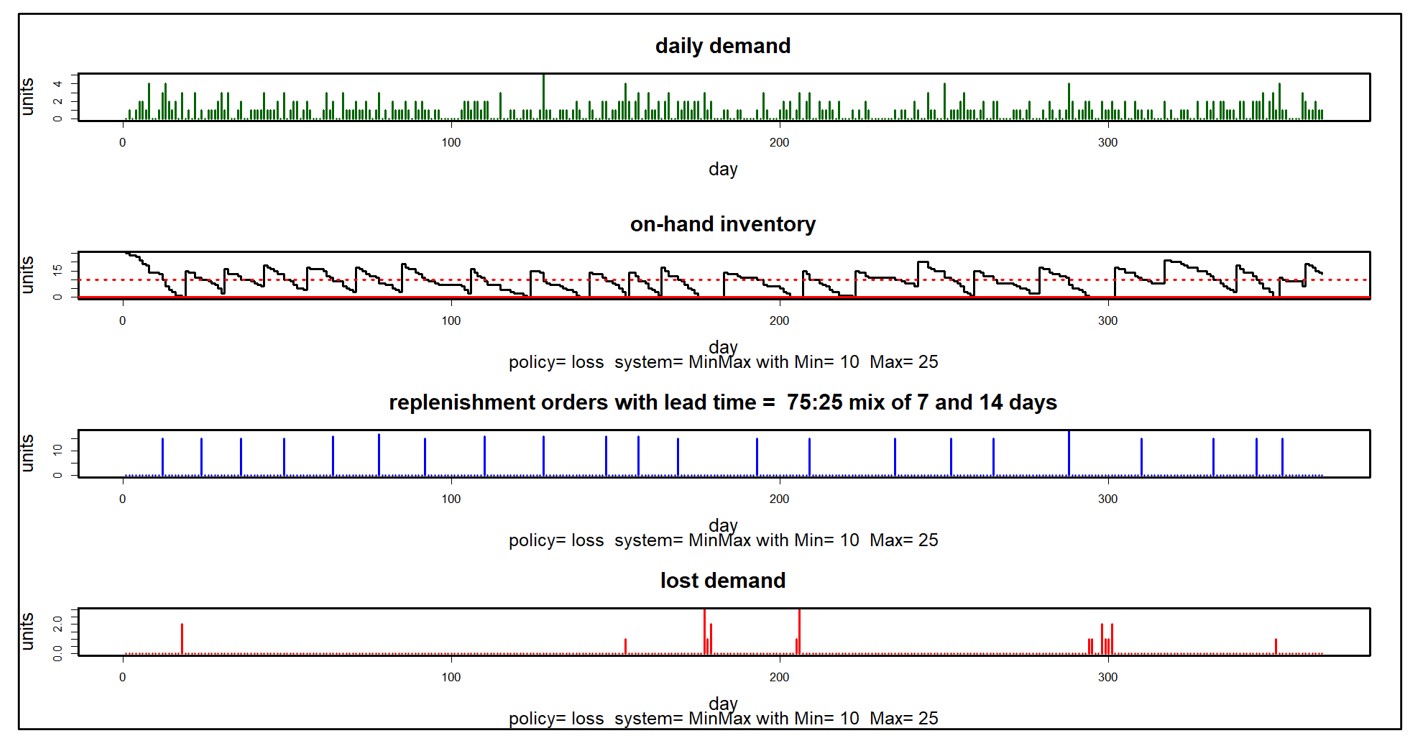
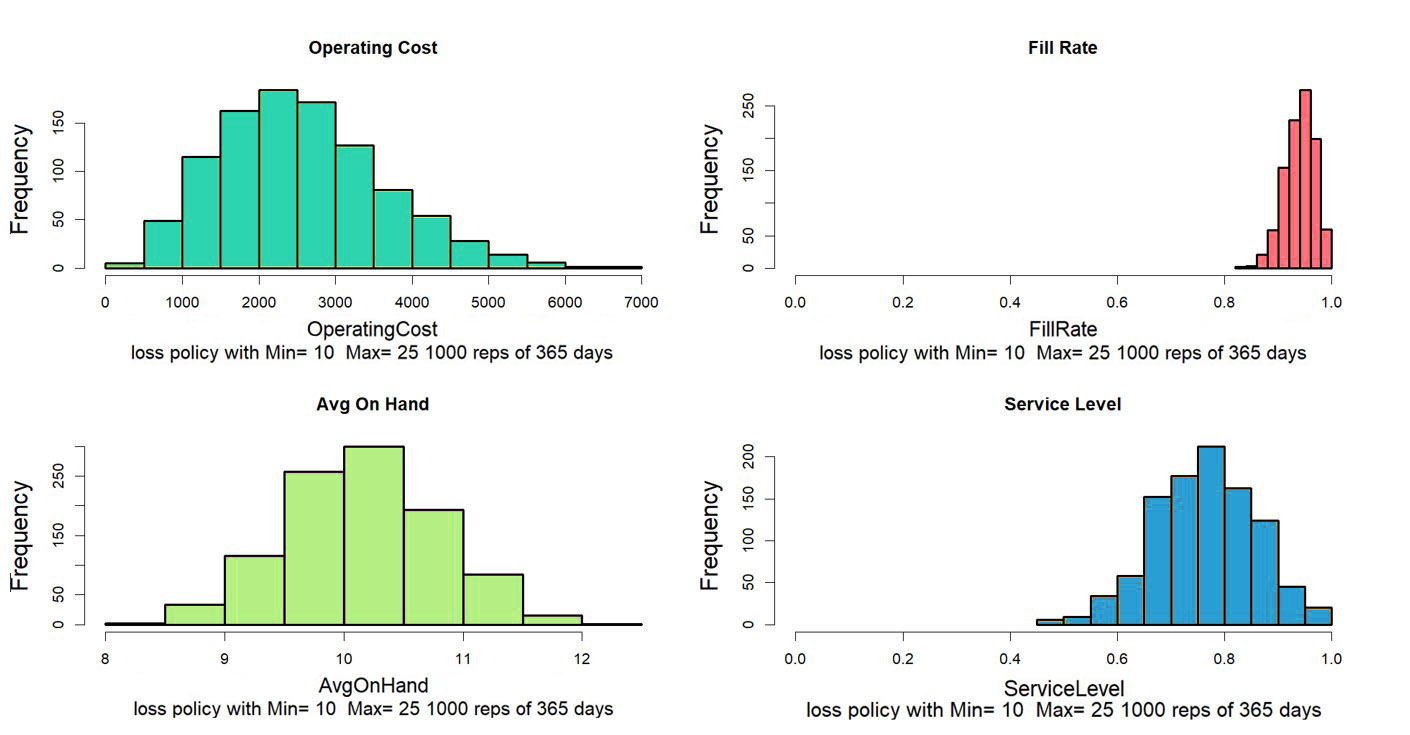
De bovengenoemde op condities gebaseerde onderhouds- en betrouwbaarheidsbenaderingen vereisen een buitensporige last voor het verzamelen en opschonen van gegevens die veel MRO-bedrijven niet aankunnen. Voor die bedrijven biedt Smart een aanpak waarbij geen betrouwbaarheidsmodellen hoeven te worden ontwikkeld. In plaats daarvan exploiteert het gebruiksgegevens op een andere manier. Het maakt gebruik van op waarschijnlijkheid gebaseerde modellen van zowel gebruik als doorlooptijden van leveranciers om duizenden mogelijke scenario's voor doorlooptijden van bevoorrading en vraag te simuleren. Het resultaat is een nauwkeurige verdeling van de vraag en de doorlooptijden voor elk verbruiksonderdeel, die kan worden benut om de optimale voorraadparameters te bepalen. Figuur 4 toont een simulatie die begint met een scenario voor de vraag naar reserveonderdelen (bovenste grafiek) en vervolgens een scenario oplevert van voorhanden aanbod voor bepaalde keuzes van Min/Max-waarden (onderste lijn). Key Performance Indicators (KPI's) kunnen worden geschat door de resultaten van veel van dergelijke simulaties te middelen.

Figuur 4: Een voorbeeld van een simulatie van de vraag naar reserveonderdelen en de voorhanden voorraad

U kunt hier lezen over de aanpak van Smart bij het voorspellen van reserveonderdelen: https://smartcorp.com/wp-content/uploads/2019/10/Probabilistic-Forecasting-for-Intermittent-Demand.pdf

Het dagelijkse voorraadbeheer kan u bezig houden. Er is het gebruikelijke ritme van bestellen, ontvangen, voorspellen en plannen, en dingen verplaatsen in het magazijn. Dan zijn er de hectische tijden – tekorten, spoedgevallen, last-minute telefoontjes om nieuwe leveranciers te vinden.

Al deze activiteiten werken tegen dat je even de tijd neemt om te kijken hoe het met je gaat. Maar je weet dat je af en toe je hoofd omhoog moet brengen om te zien waar je naartoe gaat. Daarvoor moet uw inventarissoftware u statistieken tonen – en niet slechts één, maar een volledige set statistieken of KPI's – Key Performance Indicators.

Meerdere statistieken

Afhankelijk van uw rol in uw organisatie zullen verschillende statistieken een verschillende saillantie hebben. Als u zich bezighoudt met de financiële kant van het huis, kan het investeren in inventaris van cruciaal belang zijn: hoeveel geld zit er vast in de inventaris? Als u aan de verkoopkant werkt, kan de beschikbaarheid van artikelen een prioriteit zijn: hoe groot is de kans dat ik 'ja' kan zeggen tegen een bestelling? Als u verantwoordelijk bent voor de bevoorrading, hoeveel inkooporders moeten uw mensen dan het volgende kwartaal schrappen?

Beschikbaarheidsstatistieken

Laten we teruggaan naar de beschikbaarheid van artikelen. Hoe plak je daar een getal op? De twee meest gebruikte beschikbaarheidsstatistieken zijn ‘serviceniveau’ en ‘opvullingspercentage’. Wat is het verschil? Het is het verschil tussen zeggen: “We hebben gisteren een aardbeving gehad” en zeggen: “We hebben gisteren een aardbeving gehad, en die had een kracht van 6,4 op de schaal van Richter.” Serviceniveau registreert de frequentie van stockouts, ongeacht de omvang ervan; het opvullingspercentage weerspiegelt de ernst ervan. De twee kunnen in tegengestelde richtingen lijken te wijzen, wat voor enige verwarring zorgt. U kunt een goed serviceniveau hebben, bijvoorbeeld 90%, maar een gênant opvullingspercentage, bijvoorbeeld 50%. Of vice versa. Wat hen anders maakt, is de verdeling van de vraaggroottes. Als de verdeling bijvoorbeeld erg scheef is, dus de meeste eisen zijn klein, maar sommige zijn enorm, dan kun je de hierboven genoemde 90%/50%-verdeling krijgen. Als uw focus ligt op hoe vaak u moet nabestellen, is het serviceniveau relevanter. Als u zich zorgen maakt over hoe groot een nachtelijke expedite kan worden, is het opvullingspercentage relevanter.

Eén grafiek om ze allemaal te regeren

Een grafiek van de voorhanden voorraad kan de basis vormen voor het berekenen van meerdere KPI's. Kijk eens naar Figuur 1, waarin de grafieken een jaar lang elke dag bij de hand zijn. Dit diagram bevat informatie die nodig is om meerdere statistieken te berekenen: voorraadinvestering, serviceniveau, opvullingspercentage, bestelpercentage en andere statistieken.

Voorraadinvestering: de gemiddelde hoogte van de grafiek boven nul, vermenigvuldigd met de eenheidskosten van het voorraaditem, geeft een kwartaalwaarde in dollar.

Serviceniveau: Het deel van de voorraadcycli dat boven nul eindigt, is het serviceniveau. Voorraadcycli worden gekenmerkt door de opwaartse bewegingen die worden veroorzaakt door de komst van aanvullingsorders.

Opvullingspercentage: De hoeveelheid waarmee de voorraad onder nul daalt en hoe lang de voorraad daar blijft, bepalen samen het opvullingspercentage.

In dit geval was het gemiddelde aantal beschikbare eenheden 10,74, het serviceniveau 54% en het opvullingspercentage 91%.

KPI's en KPP's

In de ruim veertig jaar sinds we Smart Software hebben opgericht, heb ik nog nooit een klant een plot als figuur 1 zien maken. Degenen die verder in hun ontwikkeling zijn, produceren en besteden aandacht aan rapporten waarin hun KPI's in tabelvorm worden vermeld, maar dat doen ze niet' Kijk niet naar zo'n grafiek. Niettemin heeft die grafiek waarde voor het ontwikkelen van inzicht in de willekeurige ritmes van de voorraad terwijl deze stijgt en daalt.

Waar het vooral nuttig is, is prospectief. Gezien de marktvolatiliteit verschuiven belangrijke variabelen zoals de doorlooptijden van leveranciers, de gemiddelde vraag en de variabiliteit van de vraag allemaal in de loop van de tijd. Dit impliceert dat belangrijke controleparameters zoals bestelpunten en bestelhoeveelheden zich aan deze verschuivingen moeten aanpassen. Als een leverancier bijvoorbeeld zegt dat hij zijn gemiddelde doorlooptijd met twee dagen moet verlengen, heeft dit een negatieve invloed op uw statistieken en moet u mogelijk uw bestelpunt verhogen om dit te compenseren. Maar met hoeveel verhogen?

Hier komt moderne inventarisatiesoftware om de hoek kijken. Hiermee kunt u een aanpassing voorstellen en vervolgens zien hoe de zaken zullen verlopen. Percelen zoals Figuur 1 laten je het nieuwe regime zien en er een gevoel voor krijgen. En de grafieken kunnen worden geanalyseerd om KPP's te berekenen: Key Performance Predictions.

De hulp van KPP maakt het giswerk bij aanpassingen overbodig. U kunt simuleren wat er met uw KPI's zal gebeuren als u deze wijzigt als reactie op veranderingen in uw werkomgeving – en hoe slecht de situatie zal zijn als u geen wijzigingen aanbrengt.

Bent u in de war over wat AI is en wat machine learning is? Weet u niet zeker waarom meer weten u zal helpen bij uw werk in voorraadplanning? Wanhoop niet. Het komt wel goed met je, en we laten je zien hoe iets van wat het ook is, nuttig kan zijn.

Wat is en wat niet

Wat is AI en waarin verschilt het van ML? Wat doet iemand tegenwoordig als hij iets wil weten? Ze Googlen het. En als ze dat doen, begint de verwarring.

Eén bron zegt dat de neurale netmethodologie, deep learning genaamd, een subset is van machine learning, een subset van AI. Maar een andere bron zegt dat deep learning al een onderdeel is van AI, omdat het min of meer de manier nabootst waarop de menselijke geest werkt, terwijl machinaal leren dat niet probeert.

Eén bron zegt dat er twee soorten machinaal leren zijn: onder toezicht en zonder toezicht. Een ander zegt dat er vier zijn: onder toezicht, zonder toezicht, semi-onder toezicht en versterking.

Sommigen zeggen dat versterkend leren machinaal leren is; anderen noemen het AI.

Sommigen van ons, traditionalisten, noemen veel ervan ‘statistieken’, hoewel dat niet allemaal zo is.

Bij het benoemen van methoden is veel ruimte voor zowel emotie als verkoopvaardigheid. Als een softwareleverancier denkt dat je de term ‘AI’ wilt horen, kan het zijn dat hij/zij dat voor je zegt, alleen maar om je blij te maken.

Het is beter om je te concentreren op wat er uiteindelijk uitkomt

Je kunt een verwarrende hype vermijden als je je concentreert op het eindresultaat dat je krijgt van een analytische technologie, ongeacht het label ervan. Er zijn verschillende analytische taken die relevant zijn voor voorraadplanners en vraagplanners. Deze omvatten clustering, detectie van afwijkingen, detectie van regimeveranderingen en regressieanalyse. Alle vier de methoden worden gewoonlijk, maar niet altijd, geclassificeerd als methoden voor machinaal leren. Maar hun algoritmen kunnen rechtstreeks uit de klassieke statistiek komen.

Clustering

Clusteren betekent het groeperen van dingen die op elkaar lijken en het distantiëren ervan van dingen die niet op elkaar lijken. Soms is clusteren eenvoudig: om uw klanten geografisch te scheiden, sorteert u ze eenvoudigweg op staat of verkoopregio. Als het probleem niet zo voor de hand liggend is, kun je data- en clusteralgoritmen gebruiken om de klus automatisch te klaren, zelfs als je met enorme datasets te maken hebt.

Figuur 1 illustreert bijvoorbeeld een cluster van “vraagprofielen”, die in dit geval alle artikelen van een klant in negen clusters verdeelt, op basis van de vorm van hun cumulatieve vraagcurven. Cluster 1.1 linksboven bevat items waarvan de vraag is afgenomen, terwijl Cluster 3.1 linksonder items bevat waarvan de vraag is toegenomen. Clusteren kan ook op leveranciers. De keuze van het aantal clusters wordt doorgaans overgelaten aan het oordeel van de gebruiker, maar ML kan die keuze begeleiden. Een gebruiker kan de software bijvoorbeeld de opdracht geven om “mijn onderdelen in vier clusters op te splitsen”, maar het gebruik van ML kan aan het licht brengen dat er in werkelijkheid zes verschillende clusters zijn die de gebruiker moet analyseren. 

Figuur 1: Artikelen clusteren op basis van de vorm van hun cumulatieve vraag

Onregelmatigheidsdetectie

Vraagvoorspelling wordt traditioneel gedaan met behulp van tijdreeksextrapolatie. Eenvoudige exponentiële afvlakking werkt bijvoorbeeld om op elk moment het ‘midden’ van de vraagverdeling te vinden en dat niveau naar voren te projecteren. Als er in het recente verleden echter een plotselinge, eenmalige stijging of daling van de vraag heeft plaatsgevonden, kan die afwijkende waarde een aanzienlijk maar onwelkom effect hebben op de kortetermijnvoorspellingen. Net zo ernstig voor de voorraadplanning, kan de anomalie een buitensporig effect hebben op de schatting van de variabiliteit van de vraag, wat rechtstreeks doorgaat naar de berekening van de veiligheidsvoorraadvereisten.

Planners geven er misschien de voorkeur aan dergelijke afwijkingen op te sporen en te verwijderen (en misschien offline follow-up te doen om de reden voor de vreemdheid te achterhalen). Maar niemand die een grote klus te klaren heeft, zal duizenden vraagdiagrammen visueel willen scannen om uitschieters op te sporen, deze uit de vraaggeschiedenis te verwijderen en vervolgens alles opnieuw te berekenen. De menselijke intelligentie zou dat kunnen doen, maar het menselijk geduld zou spoedig ophouden. Algoritmen voor het detecteren van afwijkingen zouden het werk automatisch kunnen doen met behulp van relatief eenvoudige statistische methoden. Je zou dit ‘kunstmatige intelligentie’ kunnen noemen als je dat wilt.

Detectie van regimewijzigingen

Detectie van regimeveranderingen is als de grote broer van anomaliedetectie. Regimeverandering is een aanhoudende, in plaats van tijdelijke, verschuiving in een of meer aspecten van het karakter van een tijdreeks. Terwijl de detectie van afwijkingen zich gewoonlijk richt op plotselinge verschuivingen in de gemiddelde vraag, kan een regimeverandering verschuivingen in andere kenmerken van de vraag met zich meebrengen, zoals de volatiliteit of de verdelingsvorm ervan.  

Figuur 2 illustreert een extreem voorbeeld van regimeverandering. Rond dag 120 daalde de vraag naar dit artikel op de bodem. Het voorraadbeheerbeleid en de vraagvoorspellingen op basis van de oudere gegevens zouden aan het einde van de vraaggeschiedenis enorm afwijken van de basis.

Figuur 2: Een voorbeeld van extreme regimeverandering in een artikel met een intermitterende vraag

Ook hier kunnen statistische algoritmen worden ontwikkeld om dit probleem op te lossen, en het zou eerlijk zijn om ze ‘machine learning’ of ‘kunstmatige intelligentie’ te noemen als ze daartoe gemotiveerd zijn. Door ML of AI te gebruiken om regimeveranderingen in de vraaggeschiedenis te identificeren, kan software voor vraagplanning automatisch alleen de relevante geschiedenis gebruiken bij het voorspellen, in plaats van handmatig de hoeveelheid geschiedenis te moeten kiezen die in het model moet worden geïntroduceerd. 

Regressie analyse

Regressieanalyse relateert de ene variabele aan de andere via een vergelijking. De verkoop van kozijnen in één maand kan bijvoorbeeld worden voorspeld op basis van bouwvergunningen die een paar maanden eerder zijn afgegeven. Regressieanalyse wordt al meer dan een eeuw beschouwd als onderdeel van de statistiek, maar we kunnen zeggen dat het ‘machine learning’ is, aangezien een algoritme de precieze manier uitwerkt om kennis van de ene variabele om te zetten in een voorspelling van de waarde van een andere.

Overzicht

Het is redelijk om geïnteresseerd te zijn in wat er gebeurt op het gebied van machinaal leren en kunstmatige intelligentie. Hoewel de aandacht die aan ChatGPT en zijn concurrenten wordt besteed interessant is, is deze niet relevant voor de numerieke kant van vraagplanning of voorraadbeheer. De numerieke aspecten van ML en AI zijn potentieel relevant, maar je moet proberen de wolk van hype rond deze methoden te doorzien en je te concentreren op wat ze kunnen doen. Als u de klus kunt klaren met klassieke statistische methoden, kunt u dat misschien ook doen, en vervolgens uw optie uitoefenen om het ML-label op alles wat beweegt te plakken.

Het voorspellen van voorraadbehoeften is een gespecialiseerde variant van prognoses die zich richt op de bovenkant van het bereik van mogelijke toekomstige vraag.

Beschouw voor de eenvoud het probleem van het voorspellen van de voorraadbehoeften voor slechts één periode vooruit, bijvoorbeeld één dag vooruit. Meestal bestaat de taak van forecasting uit het schatten van het meest waarschijnlijke of gemiddelde niveau van de productvraag. Als de beschikbare voorraad echter gelijk is aan de gemiddelde vraag, bestaat er een kans van ongeveer 50% dat de vraag de voorraad overtreft en resulteert in verloren omzet en/of verloren goede wil. Het instellen van het voorraadniveau op bijvoorbeeld tien keer de gemiddelde vraag zal waarschijnlijk het probleem van voorraadtekorten elimineren, maar zal net zo zeker resulteren in oplopende voorraadkosten.

De truc van voorraadoptimalisatie is om een bevredigende balans te vinden tussen voldoende voorraad hebben om aan de meeste vraag te voldoen zonder al te veel middelen in het proces vast te leggen. Meestal is de oplossing een combinatie van zakelijk inzicht en statistieken. Het beoordelende deel is het definiëren van een acceptabel voorraadserviceniveau, zoals het direct uit voorraad voldoen aan 95% vraag. Het statistische deel is om het 95e percentiel van de vraag te schatten.

Wanneer niet omgaan met Intermittent demandkunt u het vereiste voorraadniveau vaak schatten door uit te gaan van een klokvormige (normale) vraagcurve, waarbij u zowel het midden als de breedte van de klokcurve schat, en vervolgens een standaard statistische formule gebruikt om het gewenste percentiel te schatten. Het verschil tussen het gewenste voorraadniveau en het gemiddelde vraagniveau wordt de ‘veiligheidsvoorraad’ genoemd, omdat deze beschermt tegen de mogelijkheid van voorraadtekorten.

Bij een intermitterende vraag is de klokvormige curve een zeer slechte benadering van de statistische verdeling van de vraag. In dit speciale geval maakt Smart gebruik van gepatenteerde technologie voor intermitterende vraag die is ontworpen om de marges nauwkeurig te voorspellen en een betere schatting te maken van de veiligheidsvoorraad die nodig is om het vereiste voorraadserviceniveau te bereiken.

Overzicht

De geavanceerde supply chain-analyse van Smart Software maakt gebruik van meerdere geavanceerde methoden. Twee van de belangrijkste zijn "statistische bootstrapping" en "Monte Carlo-simulatie". Omdat er bij beide veel willekeurige getallen rondvliegen, raken mensen soms in de war over wat wat is en waar ze goed voor zijn. Vandaar deze notitie. Waar het op neerkomt: statistische bootstrapping genereert vraagscenario's voor prognoses. Monte Carlo-simulatie gebruikt de scenario's voor voorraadoptimalisatie.

Opstarten

Bootstrapping, ook wel "resampling" genoemd, is een methode van computationele statistieken die we gebruiken om vraagscenario's voor prognoses te creëren. De essentie van het prognoseprobleem is het blootleggen van mogelijke toekomsten waarmee uw bedrijf te maken kan krijgen, zodat u kunt uitzoeken hoe u bedrijfsrisico's kunt beheersen. Traditionele prognosemethoden richten zich op het berekenen van de "meest waarschijnlijke" toekomst, maar ze geven niet het volledige risicobeeld weer. Bootstrapping biedt een onbeperkt aantal realistische wat-als-scenario's.

Bootstrapping doet dit zonder onrealistische aannames te doen over de vraag, dwz dat deze niet intermitterend is, of dat deze een klokvormige verdeling van groottes heeft. Die aannames zijn krukken om de wiskunde eenvoudiger te maken, maar de bootstrap is een procedure, geen vergelijking, dus dergelijke vereenvoudigingen zijn niet nodig.

Voor het eenvoudigste vraagtype, dat een stabiele willekeur is zonder seizoensgebondenheid of trend, is bootstrapping doodeenvoudig. Om een redelijk idee te krijgen van wat een enkele toekomstige vraagwaarde zou kunnen zijn, kiest u willekeurig een van de historische eisen. Om een vraagscenario te creëren, maakt u meerdere willekeurige selecties uit het verleden en rijgt u ze aan elkaar. Klaar. Het is mogelijk om wat meer realisme toe te voegen door de gevraagde waarden te "jitteren", dwz een beetje extra willekeur aan elke waarde toe te voegen of af te trekken, maar zelfs dat is eenvoudig.

Figuur 1 toont een eenvoudige bootstrap. De eerste regel is een korte reeks historische vraag naar een SKU. De volgende regels tonen scenario's van toekomstige vraag die zijn gemaakt door willekeurig waarden uit de vraaggeschiedenis te selecteren. De volgende drie eisen kunnen bijvoorbeeld zijn (0, 14, 6), of (2, 3, 5), enz.

Afbeelding 1: voorbeeld van vraagscenario's gegenereerd door een eenvoudige bootstrap

Bewerkingen met een hogere frequentie, zoals dagelijkse prognoses, brengen complexere vraagpatronen met zich mee, zoals dubbele seizoensgebondenheid (bijv. dag van de week en maand van het jaar) en/of trend. Dit daagde ons uit om een nieuwe generatie bootstrapping-algoritmen uit te vinden. We hebben onlangs een Amerikaans patent gewonnen voor deze doorbraak, maar de essentie is zoals hierboven beschreven.

Monte Carlo simulatie

Monte Carlo staat bekend om zijn casino's, die net als bootstrapping het idee van willekeur oproepen. Monte Carlo-methoden gaan ver terug, maar de moderne impuls kwam met de noodzaak om wat harige berekeningen te maken over waar neutronen zouden vliegen als een A-bom ontploft.

De essentie van Monte Carlo-analyse is deze: “Ons probleem is te ingewikkeld om te analyseren met vergelijkingen van papier en potlood. Dus, laten we een computerprogramma schrijven dat de individuele stappen van het proces codeert, de willekeurige elementen erin stoppen (bijvoorbeeld welke kant een neutron op schiet), het opwinden en kijken hoe het gaat. Aangezien er veel willekeur is, laten we het programma een ontelbaar aantal keren uitvoeren en het gemiddelde van de resultaten nemen.”

Als we deze benadering toepassen op voorraadbeheer, hebben we een andere reeks willekeurig voorkomende gebeurtenissen: een vraag van een bepaalde omvang komt bijvoorbeeld op een willekeurige dag binnen, een aanvulling van een bepaalde omvang arriveert na een willekeurige doorlooptijd, we snijden een aanvullings-PO van een bepaalde maat wanneer de voorraad daalt tot of onder een bepaald bestelpunt. We coderen de logica die deze gebeurtenissen met elkaar in verband brengt in een programma. We voeden het met een willekeurige vraagvolgorde (zie bootstrapping hierboven), voeren het programma een tijdje uit, laten we zeggen een jaar dagelijkse bewerkingen, berekenen prestatiestatistieken zoals Fill Rate en Average On Hand-inventaris, en "gooi de dobbelstenen" door het opnieuw uit te voeren het programma vele malen en het gemiddelde van de resultaten van vele gesimuleerde jaren. Het resultaat is een goede inschatting van wat er gebeurt als we belangrijke managementbeslissingen nemen: “Als we het bestelpunt op 10 eenheden zetten en de bestelhoeveelheid op 15 eenheden, kunnen we een serviceniveau verwachten van 89% en een gemiddelde beschikbaarheid van 21 eenheden.” Wat de simulatie voor ons doet, is het blootleggen van de gevolgen van managementbeslissingen op basis van realistische vraagscenario's en solide wiskunde. Het giswerk is weg.

Figuur 2 toont enkele van de innerlijke werkingen van een Monte Carlo-simulatie van een voorraadsysteem in vier panelen. Het systeem gebruikt een Min/Max voorraadbeheerbeleid met Min=10 en Max=25. Nabestellingen zijn niet toegestaan: u heeft het goed of u verliest het bedrijf. Doorlooptijden voor aanvulling zijn meestal 7 dagen, maar soms ook 14. Deze simulatie duurde een jaar.

Het eerste paneel toont een complex willekeurig vraagscenario waarin er geen vraag is in het weekend, maar de vraag over het algemeen elke dag toeneemt van maandag tot en met vrijdag. Het tweede paneel toont het willekeurige aantal beschikbare eenheden, dat ebt en vloeit met elke aanvullingscyclus. Het derde paneel toont de willekeurige groottes en tijdstippen van aanvullingsorders die binnenkomen van de leverancier. Het laatste paneel toont de onbevredigde vraag die de klantrelaties in gevaar brengt. Dit soort detail kan erg handig zijn om inzicht te krijgen in de dynamiek van een voorraadsysteem.

Figuur 2: Details van een Monte Carlo-simulatie

Figuur 2 toont slechts een van de talloze manieren waarop het jaar zou kunnen verlopen. Over het algemeen willen we de resultaten van vele gesimuleerde jaren middelen. Niemand zou tenslotte een munt opgooien om te beslissen of het een eerlijke munt was. Figuur 3 laat zien hoe vier key performance metrics (KPI's) van jaar tot jaar variëren voor dit systeem. Sommige statistieken zijn relatief stabiel in simulaties (Fill Rate), maar andere laten meer relatieve variabiliteit zien (Operating Cost = Holding Cost + Ordering Cost + Shortage Cost). Als we de grafieken bekijken, kunnen we schatten dat de keuzes van Min=10, Max=25 leiden tot gemiddelde bedrijfskosten van ongeveer $3.000 per jaar, een opvullingspercentage van ongeveer 90%, een serviceniveau van ongeveer 75% en een gemiddelde aan Hand van ongeveer 10

Figuur 3: Variatie in KPI's berekend over 1000 gesimuleerde jaren

Het is nu zelfs mogelijk om een managementvraag van een hoger niveau te beantwoorden. We kunnen verder gaan dan "Wat gebeurt er als ik zus-en-zo doe?" naar “Wat is de best wat ik kan doen om een opvullingspercentage van ten minste 90% voor dit item te bereiken tegen de laagst mogelijke kosten?” De wiskundige  achter deze sprong zit nog een andere sleuteltechnologie genaamd "stochastische optimalisatie", maar we stoppen hier voor nu. Het volstaat te zeggen dat de SIO&P-software van Smart de "ontwerpruimte" van min- en max-waarden kan doorzoeken om automatisch de beste keuze te vinden.