Het meten van de nauwkeurigheid van prognoses is een onmiskenbaar belangrijk onderdeel van het vraagplanningsproces. Deze voorspellingsscorekaart zou kunnen worden opgebouwd op basis van een van de twee contrasterende gezichtspunten voor het berekenen van metrieken. Vanuit het foutperspectief wordt de vraag gesteld: “Hoe ver lag de voorspelling van de werkelijkheid?” Vanuit het nauwkeurigheidsperspectief wordt de vraag gesteld: “Hoe dicht lag de voorspelling bij de werkelijkheid?” Beide zijn geldig, maar foutstatistieken bieden meer informatie.

Nauwkeurigheid wordt weergegeven als een percentage tussen nul en 100, terwijl foutpercentages bij nul beginnen maar geen bovengrens hebben. Rapporten van MAPE (gemiddelde absolute procentuele fout) of andere foutstatistieken kunnen de titel 'voorspellingsnauwkeurigheid'-rapporten krijgen, waardoor het onderscheid vervaagt. Het kan dus zijn dat u wilt weten hoe u vanuit het foutenperspectief kunt overstappen naar het nauwkeurigheidsperspectief dat uw bedrijf omarmt. In deze blog wordt aan de hand van enkele voorbeelden beschreven hoe.

Nauwkeurigheidsgegevens worden zo berekend dat wanneer de werkelijke waarde gelijk is aan de voorspelling, de nauwkeurigheid 100% is en wanneer de voorspelling het dubbele of de helft is van de werkelijke, de nauwkeurigheid 0% is. Rapporten waarin de voorspelling met de werkelijkheid wordt vergeleken, bevatten vaak het volgende:

• De daadwerkelijke
• De prognose
• Eenheidsfout = Prognose – Werkelijk
• Absolute fout = Absolute waarde van eenheidsfout
• Absolute %-fout = Abs-fout / Werkelijk, als een %
• Nauwkeurigheid % = 100% – Absolute %-fout

Bekijk een paar voorbeelden die het verschil in aanpak illustreren. Stel dat de Werkelijke = 8 en de voorspelling is 10.

Eenheidsfout is 10 – 8 = 2

Absolute %-fout = 2/8, als % = 0,25 * 100 = 25%

Nauwkeurigheid = 100% – 25% = 75%.

Laten we nu zeggen dat de werkelijke waarde 8 is en de voorspelling 24.

Eenheidsfout is 24– 8 = 16

Absolute %-fout = 16/8 als % = 2 * 100 = 200%

Nauwkeurigheid = 100% – 200% = negatief is ingesteld op 0%.

In het eerste voorbeeld leveren nauwkeurigheidsmetingen dezelfde informatie op als foutmetingen, aangezien de voorspelling en de werkelijke situatie al relatief dicht bij elkaar liggen. Maar als de fout meer dan het dubbele is van de werkelijke, komen de nauwkeurigheidsmetingen uit op nul. Het geeft wel correct aan dat de voorspelling helemaal niet accuraat was. Maar het tweede voorbeeld is nauwkeuriger dan een derde, waarbij de werkelijke waarde 8 is en de voorspelling 200. Dat is een onderscheid dat een nauwkeurigheidsbereik van 0 tot 100% niet registreert. In dit laatste voorbeeld:

Eenheidsfout is 200 – 8 = 192

Absolute %-fout = 192/8, als % = 24 * 100 = 2,400%

Nauwkeurigheid = 100% – 2.400% = negatief is ingesteld op 0%.

Foutstatistieken blijven informatie verschaffen over hoe ver de voorspelling afwijkt van de werkelijke en geven aantoonbaar een betere weergave van de nauwkeurigheid van de voorspelling.

Wij moedigen aan om het foutperspectief te hanteren. U hoopt eenvoudigweg op een klein foutpercentage dat aangeeft dat de voorspelling niet ver van de werkelijkheid ligt, in plaats van te hopen op een groot nauwkeurigheidspercentage dat aangeeft dat de voorspelling dicht bij de werkelijkheid ligt. Deze mentaliteitsverandering biedt dezelfde inzichten en elimineert vervormingen.

Het dagelijkse voorraadbeheer kan u bezig houden. Er is het gebruikelijke ritme van bestellen, ontvangen, voorspellen en plannen, en dingen verplaatsen in het magazijn. Dan zijn er de hectische tijden – tekorten, spoedgevallen, last-minute telefoontjes om nieuwe leveranciers te vinden.

Al deze activiteiten werken tegen dat je even de tijd neemt om te kijken hoe het met je gaat. Maar je weet dat je af en toe je hoofd omhoog moet brengen om te zien waar je naartoe gaat. Daarvoor moet uw inventarissoftware u statistieken tonen – en niet slechts één, maar een volledige set statistieken of KPI's – Key Performance Indicators.

Meerdere statistieken

Afhankelijk van uw rol in uw organisatie zullen verschillende statistieken een verschillende saillantie hebben. Als u zich bezighoudt met de financiële kant van het huis, kan het investeren in inventaris van cruciaal belang zijn: hoeveel geld zit er vast in de inventaris? Als u aan de verkoopkant werkt, kan de beschikbaarheid van artikelen een prioriteit zijn: hoe groot is de kans dat ik 'ja' kan zeggen tegen een bestelling? Als u verantwoordelijk bent voor de bevoorrading, hoeveel inkooporders moeten uw mensen dan het volgende kwartaal schrappen?

Beschikbaarheidsstatistieken

Laten we teruggaan naar de beschikbaarheid van artikelen. Hoe plak je daar een getal op? De twee meest gebruikte beschikbaarheidsstatistieken zijn ‘serviceniveau’ en ‘opvullingspercentage’. Wat is het verschil? Het is het verschil tussen zeggen: “We hebben gisteren een aardbeving gehad” en zeggen: “We hebben gisteren een aardbeving gehad, en die had een kracht van 6,4 op de schaal van Richter.” Serviceniveau registreert de frequentie van stockouts, ongeacht de omvang ervan; het opvullingspercentage weerspiegelt de ernst ervan. De twee kunnen in tegengestelde richtingen lijken te wijzen, wat voor enige verwarring zorgt. U kunt een goed serviceniveau hebben, bijvoorbeeld 90%, maar een gênant opvullingspercentage, bijvoorbeeld 50%. Of vice versa. Wat hen anders maakt, is de verdeling van de vraaggroottes. Als de verdeling bijvoorbeeld erg scheef is, dus de meeste eisen zijn klein, maar sommige zijn enorm, dan kun je de hierboven genoemde 90%/50%-verdeling krijgen. Als uw focus ligt op hoe vaak u moet nabestellen, is het serviceniveau relevanter. Als u zich zorgen maakt over hoe groot een nachtelijke expedite kan worden, is het opvullingspercentage relevanter.

Eén grafiek om ze allemaal te regeren

Een grafiek van de voorhanden voorraad kan de basis vormen voor het berekenen van meerdere KPI's. Kijk eens naar Figuur 1, waarin de grafieken een jaar lang elke dag bij de hand zijn. Dit diagram bevat informatie die nodig is om meerdere statistieken te berekenen: voorraadinvestering, serviceniveau, opvullingspercentage, bestelpercentage en andere statistieken.

Voorraadinvestering: de gemiddelde hoogte van de grafiek boven nul, vermenigvuldigd met de eenheidskosten van het voorraaditem, geeft een kwartaalwaarde in dollar.

Serviceniveau: Het deel van de voorraadcycli dat boven nul eindigt, is het serviceniveau. Voorraadcycli worden gekenmerkt door de opwaartse bewegingen die worden veroorzaakt door de komst van aanvullingsorders.

Opvullingspercentage: De hoeveelheid waarmee de voorraad onder nul daalt en hoe lang de voorraad daar blijft, bepalen samen het opvullingspercentage.

In dit geval was het gemiddelde aantal beschikbare eenheden 10,74, het serviceniveau 54% en het opvullingspercentage 91%.

KPI's en KPP's

In de ruim veertig jaar sinds we Smart Software hebben opgericht, heb ik nog nooit een klant een plot als figuur 1 zien maken. Degenen die verder in hun ontwikkeling zijn, produceren en besteden aandacht aan rapporten waarin hun KPI's in tabelvorm worden vermeld, maar dat doen ze niet' Kijk niet naar zo'n grafiek. Niettemin heeft die grafiek waarde voor het ontwikkelen van inzicht in de willekeurige ritmes van de voorraad terwijl deze stijgt en daalt.

Waar het vooral nuttig is, is prospectief. Gezien de marktvolatiliteit verschuiven belangrijke variabelen zoals de doorlooptijden van leveranciers, de gemiddelde vraag en de variabiliteit van de vraag allemaal in de loop van de tijd. Dit impliceert dat belangrijke controleparameters zoals bestelpunten en bestelhoeveelheden zich aan deze verschuivingen moeten aanpassen. Als een leverancier bijvoorbeeld zegt dat hij zijn gemiddelde doorlooptijd met twee dagen moet verlengen, heeft dit een negatieve invloed op uw statistieken en moet u mogelijk uw bestelpunt verhogen om dit te compenseren. Maar met hoeveel verhogen?

Hier komt moderne inventarisatiesoftware om de hoek kijken. Hiermee kunt u een aanpassing voorstellen en vervolgens zien hoe de zaken zullen verlopen. Percelen zoals Figuur 1 laten je het nieuwe regime zien en er een gevoel voor krijgen. En de grafieken kunnen worden geanalyseerd om KPP's te berekenen: Key Performance Predictions.

De hulp van KPP maakt het giswerk bij aanpassingen overbodig. U kunt simuleren wat er met uw KPI's zal gebeuren als u deze wijzigt als reactie op veranderingen in uw werkomgeving – en hoe slecht de situatie zal zijn als u geen wijzigingen aanbrengt.

Bent u in de war over wat AI is en wat machine learning is? Weet u niet zeker waarom meer weten u zal helpen bij uw werk in voorraadplanning? Wanhoop niet. Het komt wel goed met je, en we laten je zien hoe iets van wat het ook is, nuttig kan zijn.

Wat is en wat niet

Wat is AI en waarin verschilt het van ML? Wat doet iemand tegenwoordig als hij iets wil weten? Ze Googlen het. En als ze dat doen, begint de verwarring.

Eén bron zegt dat de neurale netmethodologie, deep learning genaamd, een subset is van machine learning, een subset van AI. Maar een andere bron zegt dat deep learning al een onderdeel is van AI, omdat het min of meer de manier nabootst waarop de menselijke geest werkt, terwijl machinaal leren dat niet probeert.

Eén bron zegt dat er twee soorten machinaal leren zijn: onder toezicht en zonder toezicht. Een ander zegt dat er vier zijn: onder toezicht, zonder toezicht, semi-onder toezicht en versterking.

Sommigen zeggen dat versterkend leren machinaal leren is; anderen noemen het AI.

Sommigen van ons, traditionalisten, noemen veel ervan ‘statistieken’, hoewel dat niet allemaal zo is.

Bij het benoemen van methoden is veel ruimte voor zowel emotie als verkoopvaardigheid. Als een softwareleverancier denkt dat je de term ‘AI’ wilt horen, kan het zijn dat hij/zij dat voor je zegt, alleen maar om je blij te maken.

Het is beter om je te concentreren op wat er uiteindelijk uitkomt

Je kunt een verwarrende hype vermijden als je je concentreert op het eindresultaat dat je krijgt van een analytische technologie, ongeacht het label ervan. Er zijn verschillende analytische taken die relevant zijn voor voorraadplanners en vraagplanners. Deze omvatten clustering, detectie van afwijkingen, detectie van regimeveranderingen en regressieanalyse. Alle vier de methoden worden gewoonlijk, maar niet altijd, geclassificeerd als methoden voor machinaal leren. Maar hun algoritmen kunnen rechtstreeks uit de klassieke statistiek komen.

Clustering

Clusteren betekent het groeperen van dingen die op elkaar lijken en het distantiëren ervan van dingen die niet op elkaar lijken. Soms is clusteren eenvoudig: om uw klanten geografisch te scheiden, sorteert u ze eenvoudigweg op staat of verkoopregio. Als het probleem niet zo voor de hand liggend is, kun je data- en clusteralgoritmen gebruiken om de klus automatisch te klaren, zelfs als je met enorme datasets te maken hebt.

Figuur 1 illustreert bijvoorbeeld een cluster van “vraagprofielen”, die in dit geval alle artikelen van een klant in negen clusters verdeelt, op basis van de vorm van hun cumulatieve vraagcurven. Cluster 1.1 linksboven bevat items waarvan de vraag is afgenomen, terwijl Cluster 3.1 linksonder items bevat waarvan de vraag is toegenomen. Clusteren kan ook op leveranciers. De keuze van het aantal clusters wordt doorgaans overgelaten aan het oordeel van de gebruiker, maar ML kan die keuze begeleiden. Een gebruiker kan de software bijvoorbeeld de opdracht geven om “mijn onderdelen in vier clusters op te splitsen”, maar het gebruik van ML kan aan het licht brengen dat er in werkelijkheid zes verschillende clusters zijn die de gebruiker moet analyseren. 

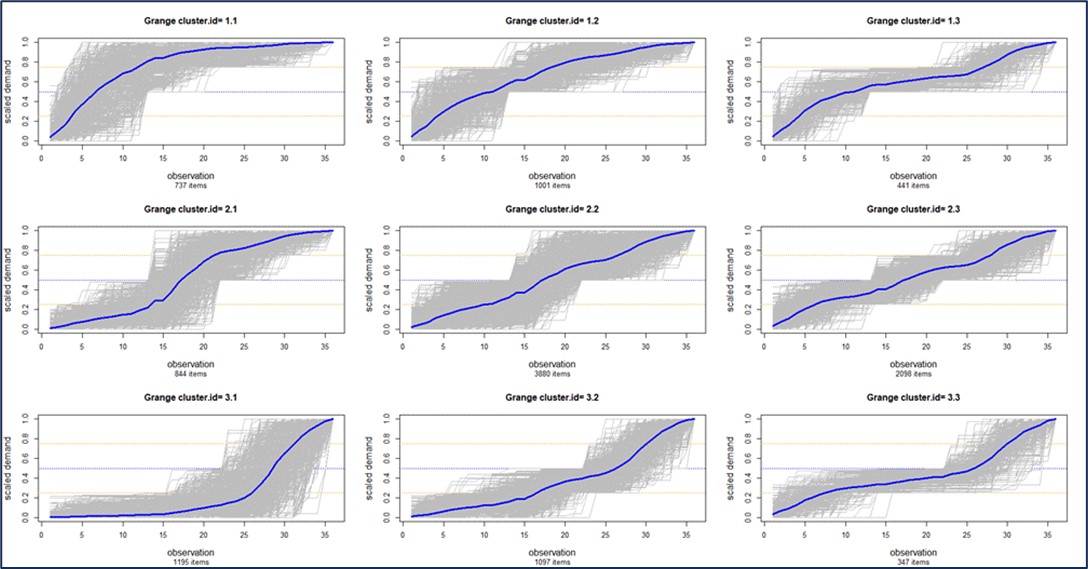
Figuur 1: Artikelen clusteren op basis van de vorm van hun cumulatieve vraag

Onregelmatigheidsdetectie

Vraagvoorspelling wordt traditioneel gedaan met behulp van tijdreeksextrapolatie. Eenvoudige exponentiële afvlakking werkt bijvoorbeeld om op elk moment het ‘midden’ van de vraagverdeling te vinden en dat niveau naar voren te projecteren. Als er in het recente verleden echter een plotselinge, eenmalige stijging of daling van de vraag heeft plaatsgevonden, kan die afwijkende waarde een aanzienlijk maar onwelkom effect hebben op de kortetermijnvoorspellingen. Net zo ernstig voor de voorraadplanning, kan de anomalie een buitensporig effect hebben op de schatting van de variabiliteit van de vraag, wat rechtstreeks doorgaat naar de berekening van de veiligheidsvoorraadvereisten.

Planners geven er misschien de voorkeur aan dergelijke afwijkingen op te sporen en te verwijderen (en misschien offline follow-up te doen om de reden voor de vreemdheid te achterhalen). Maar niemand die een grote klus te klaren heeft, zal duizenden vraagdiagrammen visueel willen scannen om uitschieters op te sporen, deze uit de vraaggeschiedenis te verwijderen en vervolgens alles opnieuw te berekenen. De menselijke intelligentie zou dat kunnen doen, maar het menselijk geduld zou spoedig ophouden. Algoritmen voor het detecteren van afwijkingen zouden het werk automatisch kunnen doen met behulp van relatief eenvoudige statistische methoden. Je zou dit ‘kunstmatige intelligentie’ kunnen noemen als je dat wilt.

Detectie van regimewijzigingen

Detectie van regimeveranderingen is als de grote broer van anomaliedetectie. Regimeverandering is een aanhoudende, in plaats van tijdelijke, verschuiving in een of meer aspecten van het karakter van een tijdreeks. Terwijl de detectie van afwijkingen zich gewoonlijk richt op plotselinge verschuivingen in de gemiddelde vraag, kan een regimeverandering verschuivingen in andere kenmerken van de vraag met zich meebrengen, zoals de volatiliteit of de verdelingsvorm ervan.  

Figuur 2 illustreert een extreem voorbeeld van regimeverandering. Rond dag 120 daalde de vraag naar dit artikel op de bodem. Het voorraadbeheerbeleid en de vraagvoorspellingen op basis van de oudere gegevens zouden aan het einde van de vraaggeschiedenis enorm afwijken van de basis.

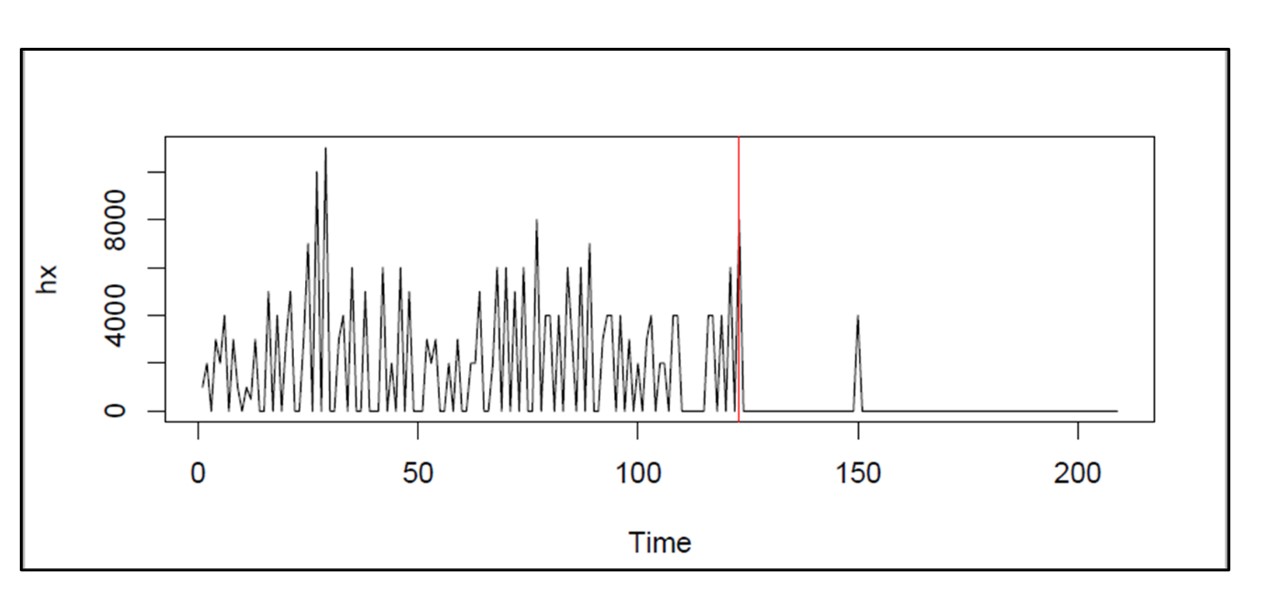
Figuur 2: Een voorbeeld van extreme regimeverandering in een artikel met een intermitterende vraag

Ook hier kunnen statistische algoritmen worden ontwikkeld om dit probleem op te lossen, en het zou eerlijk zijn om ze ‘machine learning’ of ‘kunstmatige intelligentie’ te noemen als ze daartoe gemotiveerd zijn. Door ML of AI te gebruiken om regimeveranderingen in de vraaggeschiedenis te identificeren, kan software voor vraagplanning automatisch alleen de relevante geschiedenis gebruiken bij het voorspellen, in plaats van handmatig de hoeveelheid geschiedenis te moeten kiezen die in het model moet worden geïntroduceerd. 

Regressie analyse

Regressieanalyse relateert de ene variabele aan de andere via een vergelijking. De verkoop van kozijnen in één maand kan bijvoorbeeld worden voorspeld op basis van bouwvergunningen die een paar maanden eerder zijn afgegeven. Regressieanalyse wordt al meer dan een eeuw beschouwd als onderdeel van de statistiek, maar we kunnen zeggen dat het ‘machine learning’ is, aangezien een algoritme de precieze manier uitwerkt om kennis van de ene variabele om te zetten in een voorspelling van de waarde van een andere.

Overzicht

Het is redelijk om geïnteresseerd te zijn in wat er gebeurt op het gebied van machinaal leren en kunstmatige intelligentie. Hoewel de aandacht die aan ChatGPT en zijn concurrenten wordt besteed interessant is, is deze niet relevant voor de numerieke kant van vraagplanning of voorraadbeheer. De numerieke aspecten van ML en AI zijn potentieel relevant, maar je moet proberen de wolk van hype rond deze methoden te doorzien en je te concentreren op wat ze kunnen doen. Als u de klus kunt klaren met klassieke statistische methoden, kunt u dat misschien ook doen, en vervolgens uw optie uitoefenen om het ML-label op alles wat beweegt te plakken.

Het voorspellen van voorraadbehoeften is een gespecialiseerde variant van prognoses die zich richt op de bovenkant van het bereik van mogelijke toekomstige vraag.

Beschouw voor de eenvoud het probleem van het voorspellen van de voorraadbehoeften voor slechts één periode vooruit, bijvoorbeeld één dag vooruit. Meestal bestaat de taak van forecasting uit het schatten van het meest waarschijnlijke of gemiddelde niveau van de productvraag. Als de beschikbare voorraad echter gelijk is aan de gemiddelde vraag, bestaat er een kans van ongeveer 50% dat de vraag de voorraad overtreft en resulteert in verloren omzet en/of verloren goede wil. Het instellen van het voorraadniveau op bijvoorbeeld tien keer de gemiddelde vraag zal waarschijnlijk het probleem van voorraadtekorten elimineren, maar zal net zo zeker resulteren in oplopende voorraadkosten.

De truc van voorraadoptimalisatie is om een bevredigende balans te vinden tussen voldoende voorraad hebben om aan de meeste vraag te voldoen zonder al te veel middelen in het proces vast te leggen. Meestal is de oplossing een combinatie van zakelijk inzicht en statistieken. Het beoordelende deel is het definiëren van een acceptabel voorraadserviceniveau, zoals het direct uit voorraad voldoen aan 95% vraag. Het statistische deel is om het 95e percentiel van de vraag te schatten.

Wanneer niet omgaan met Intermittent demandkunt u het vereiste voorraadniveau vaak schatten door uit te gaan van een klokvormige (normale) vraagcurve, waarbij u zowel het midden als de breedte van de klokcurve schat, en vervolgens een standaard statistische formule gebruikt om het gewenste percentiel te schatten. Het verschil tussen het gewenste voorraadniveau en het gemiddelde vraagniveau wordt de ‘veiligheidsvoorraad’ genoemd, omdat deze beschermt tegen de mogelijkheid van voorraadtekorten.

Bij een intermitterende vraag is de klokvormige curve een zeer slechte benadering van de statistische verdeling van de vraag. In dit speciale geval maakt Smart gebruik van gepatenteerde technologie voor intermitterende vraag die is ontworpen om de marges nauwkeurig te voorspellen en een betere schatting te maken van de veiligheidsvoorraad die nodig is om het vereiste voorraadserviceniveau te bereiken.

Automatische prognoses zijn de populairste en meest gebruikte functie van SmartForecasts en Smart Demand Planner. Automatische prognoses maken is eenvoudig. Maar de eenvoud van Automatic Forecasting maskeert een krachtige interactie van een aantal zeer effectieve prognosemethoden. In deze blog bespreken we een deel van de theorie achter deze kernfunctie. We richten ons op automatische prognoses, deels vanwege de populariteit ervan en deels omdat veel andere prognosemethoden vergelijkbare resultaten opleveren. Kennis van automatische prognoses wordt onmiddellijk overgedragen naar eenvoudig voortschrijdend gemiddelde, lineair voortschrijdend gemiddelde, enkele exponentiële afvlakking, dubbele exponentiële afvlakking, Winters' exponentiële afvlakking en promoprognoses.

Prognose toernooi

Automatische prognoses werken door een toernooi uit te voeren met een reeks concurrerende methoden. Omdat personal computers en cloud computing snel zijn, en omdat we zeer efficiënte algoritmen hebben gecodeerd in de automatische voorspellingsengine van SmartForecasts, is het praktisch om een puur empirische benadering te volgen om te beslissen welke extrapolatieve voorspellingsmethode moet worden gebruikt. Dit betekent dat u het zich kunt veroorloven om een aantal benaderingen uit te proberen en vervolgens degene te behouden die het beste presteert bij het voorspellen van de betreffende gegevensreeks. SmartForecasts automatiseert dit proces volledig voor u door de verschillende voorspellingsmethoden uit te proberen in een gesimuleerd voorspellingstoernooi. De winnaar van het toernooi is de methode die het dichtst bij het voorspellen van nieuwe gegevenswaarden van oude komt. Nauwkeurigheid wordt gemeten aan de hand van de gemiddelde absolute fout (dat wil zeggen de gemiddelde fout, waarbij eventuele mintekens worden genegeerd). Het gemiddelde wordt berekend over een reeks voorspellingen, die elk een deel van de gegevens gebruiken, in een proces dat bekend staat als glijdende simulatie.

Glijdende simulatie

De glijdende simulatie veegt herhaaldelijk door steeds langere delen van de historische gegevens, waarbij in elk geval het gewenste aantal perioden in uw prognosehorizon wordt voorspeld. Stel dat er 36 historische gegevenswaarden zijn en dat u zes perioden vooruit moet voorspellen. Stel je voor dat je de voorspellingsnauwkeurigheid van een bepaalde methode, bijvoorbeeld een voortschrijdend gemiddelde van vier waarnemingen, wilt beoordelen op de gegevensreeks die voorhanden is.

Op een gegeven moment in de glijdende simulatie worden de eerste 24 punten (alleen) gebruikt om de 25e tot en met 30e historische gegevenswaarden te voorspellen, die we tijdelijk als onbekend beschouwen. We zeggen dat de punten 25-30 buiten de analyse worden gehouden. Het berekenen van de absolute waarden van de verschillen tussen de zes prognoses en de overeenkomstige werkelijke historische waarden levert één exemplaar op van elk een 1-staps, 2-staps, 3-staps, 4-staps, 5-staps en 6-staps vooruit absolute voorspelling fout. Als u dit proces herhaalt met de eerste 25 punten, krijgt u meer voorbeelden van 1-staps, 2-staps, 3-staps vooruit-fouten, enzovoort. Het gemiddelde van alle absolute foutschattingen die op deze manier zijn verkregen, geeft een samenvatting van de nauwkeurigheid in één getal.

Methoden die worden gebruikt bij automatische prognoses

Normaal gesproken zijn er zes extrapolatieve voorspellingsmethoden die meedoen aan het automatische voorspellingstoernooi:

• Eenvoudig voortschrijdend gemiddelde
• Lineair voortschrijdend gemiddelde
• Enkele exponentiële afvlakking
• Dubbele exponentiële afvlakking
• Additieve versie van Winters' exponentiële afvlakking
• Multiplicatieve versie van Winters' exponentiële afvlakking

De laatste twee methoden zijn geschikt voor seizoenreeksen; ze worden echter automatisch uitgesloten van het toernooi als er minder dan twee volledige seizoensgegevenscycli zijn (bijvoorbeeld minder dan 24 periodes met maandelijkse gegevens of acht periodes met driemaandelijkse gegevens).

Deze zes klassieke, op afvlakking gebaseerde methoden hebben bewezen gemakkelijk te begrijpen, gemakkelijk te berekenen en nauwkeurig te zijn. Je kunt elk van deze methoden uitsluiten van het toernooi als je een voorkeur hebt voor sommige deelnemers en niet voor andere.