Los objetivos de suministro diarios no funcionan al calcular las existencias de seguridad

Los CFO nos dicen que necesitan gastar menos en inventario y sin que afecte a las ventas. Una forma de hacerlo es dejar de usar los objetivos diarios de suministro para determinar los puntos de pedido y las reservas de existencias de seguridad. Así es como funciona un modelo de suministro diario:

1. Calcule el promedioa de la demanda diaria y multiplique la demanda diaria por el tiempo de entrega del proveedor por días para obtener la demanda de tiempo de entrega
2. Elija un búfer de suministro por días (es decir, 15, 30, 45 días, etc.). Use búferes más grandes para elementos más importantes y búferes más pequeños para elementos menos importantes.
3. Agregue los días de reserva deseados del suministro a la demanda durante el tiempo de entrega para obtener el punto de reorden. Pida más cuando el inventario disponible esté por debajo del punto de reorden.

Este enfoque es erroneo por las siguientes razones:

1. El promedio no tiene en cuenta la estacionalidad ni la tendencia: no verá patrones obvios a menos que pase mucho tiempo ajustándolos manualmente.
2. El promedio no tiene en cuenta cuán predecible es un artículo: tendrá un exceso de existencias de artículos predecibles y una escasez de artículos menos predecibles. Esto se debe a que los mismos días de suministro para diferentes artículos generan un riesgo de agotamiento de existencias muy diferente.
3. El promedio no le dice a un planificador cómo el nivel de inventario afecta el riesgo de falta de existencias: no tendrá idea de si tiene existencias insuficientes, excesivas o si tiene suficiente.

Hay muchos otros enfoques de "regla general" que son igualmente problemáticos. Puedes aprender más sobre ellos en este blog. 

Una mejor manera de planificar la cantidad correcta del inventario de seguridad es aprovechar los modelos de probabilidad que identifican exactamente cuánto inventario se necesita contando el riesgo de desabastecimiento que está dispuesto a aceptar. A continuación se muestra una captura de pantalla de Smart Inventory Optimization que hace exactamente eso. En primer lugar, detalla los niveles de servicio previstos (probabilidad de no agotarse) asociados con la lógica de suministro de los días actuales. El planificador ahora puede ver las partes en las que el nivel de servicio previsto es demasiado bajo o demasiado costoso. Luego pueden hacer correcciones inmediatas enfocándose en los niveles de servicio deseados y el nivel de inversión en inventario. Sin esta información, un planificador no sabrá si los días previstos de existencias de seguridad son demasiado, demasiado poco o simplemente correctos, lo que resulta en excesos y escasez que cuestan participación de mercado e ingresos. 

Al decidir los parámetros correctos de almacenamiento de repuestos y piezas de servicio, es importante distinguir entre piezas de servicio consumibles y reparables. Estas diferencias a menudo son pasadas por alto por el servicio software de planificación de piezas y puede resultar en errores estimaciones de los requisitos de almacenaje. Se requieren diferentes enfoques al planificar los consumibles frente a las piezas de repuesto reparables.

Primero, definamos estos dos tipos de repuestos.

• Partes consumibles son repuestos contenidos dentro del equipo que se reemplazan en lugar de repararse cuando fallan. Los ejemplos de piezas consumibles incluyen baterías, filtros de aceite, tornillos, pastillas de freno, etc. Las piezas de repuesto consumibles tienden a ser piezas de menor costo para las cuales el reemplazo es más barato que la reparación o la reparación puede no ser posible.
• Partes reparables son piezas que se pueden reparar y volver a poner en servicio después de fallar debido a causas como desgaste, daños o corrosión. Las piezas de servicio reparables tienden a ser más caras que las piezas consumibles, por lo que la reparación suele ser preferible al reemplazo. Los ejemplos de piezas reparables incluyen motores de tracción en vagones de ferrocarril, motores a reacción, fotocopiadoras, etc.

El software tradicional de planificación de piezas de repuesto no cumple con los requisitos

El software tradicional de planificación de piezas no está bien adaptado para lidiar con la aleatoriedad tanto en el lado de la demanda como en el lado de la oferta de las operaciones de MRO.

Aleatoriedad del lado de la demanda
La planificación de repuestos consumibles requiere el cálculo de parámetros de control de inventario (como puntos de pedido y cantidades de pedido, niveles mínimo y máximo y existencias de seguridad). La planificación para administrar las piezas de servicio reparables requiere el cálculo de la cantidad correcta de repuestos. En ambos casos, el análisis debe basarse en modelos de probabilidad del uso aleatorio de consumibles o la avería aleatoria de piezas reparables. Para más de 90% de estas partes, la demanda es “intermitente” (a veces llamado "érratica"). Los métodos tradicionales de previsión de repuestos no se desarrollaron para hacer frente a la demanda intermitente. Confiar en los métodos tradicionales conduce a costosos errores de planificación. Para los consumibles, esto significa desabastecimientos evitables, costos excesivos de mantenimiento y mayor obsolescencia del inventario. Para las piezas reparables, esto significa un tiempo de inactividad excesivo del equipo y los costos correspondientes por un rendimiento poco confiable y la interrupción de las operaciones.

Aleatoriedad del lado de la oferta
La planificación de piezas de repuesto consumibles debe tener en cuenta la aleatoriedad en el reabastecimiento de los plazos de entrega de los proveedores. La planificación de piezas reparables debe tener en cuenta la aleatoriedad en los procesos de reparación y devolución, ya sea que de los que se proporcionen internamente o se contraten. Los planificadores que gestionan estos artículos a menudo ignoran los datos de interés dentro de la empresa. En cambio, pueden cruzar los dedos y esperar que todo salga bien, o pueden invocar su instinto para "selecionar a ojo" y luego esperar que todo salga bien. Esperar y adivinar no puede vencer al modelo de probabilidad adecuado. Desperdicia millones anualmente en inversiones de capital innecesarias y tiempo de inactividad evitable del equipo.

Ya sea que esté utilizando 'Mín./Máx.' o 'punto de pedido' y 'cantidad de pedido' para determinar cuándo y cuánto reabastecer, su enfoque puede generar o negar grandes eficiencias. Errores clave a evitar:

1. No recalibrar regularmente
2. Si se revisa solo el Min/Max, hay un problema
3. El uso de métodos de pronóstico no está a la altura de la tarea
4. Asumir que los datos son demasiado lentos o impredecibles

“Tenemos más de 150.000 combinaciones SKU x Ubicación. Nuestra demanda es intermitente. Dado que se mueve lentamente, no necesitamos volver a calcular nuestros puntos de pedido con frecuencia. Lo hacemos tal vez una vez al año, pero revisamos los puntos de pedido cada vez que hay un problema”. – Gerente de Materiales.

Este enfoque reactivo conducirá a millones en exceso de existencias, roturas de existencias y mucho tiempo perdido revisando datos cuando "algo sale mal". Sin embargo, he escuchado este mismo estribillo a muchos profesionales de inventario a lo largo de los años. Claramente, necesitamos compartir porqué este pensamiento es totalmente erróneo.

Es cierto que para muchas partes, un recálculo de los puntos de pedido con datos históricos actualizados y plazos de entrega podría no cambiar mucho, especialmente si hay patrones como la tendencia o la estacionalidad. Sin embargo, muchas partes se beneficiarán de un recálculo, especialmente si los plazos de entrega o la demanda reciente han cambiado. Además, la probabilidad de un cambio significativo que requiera un nuevo cálculo aumenta cuanto más espere. Finalmente, esos meses con nula demanda también influyen en las probabilidades y no deben ser ignorados. Sin embargo, el punto clave es que es imposible saber qué cambiará o no cambiará en su pronóstico, por lo que es mejor recalibrar regularmente.

Este caso de datos real ilustra un escenario donde brilla la recalibración regular y automatizada: los beneficios de las respuestas rápidas a patrones de demanda cambiantes y como estos se suman rápidamente. En el ejemplo anterior, el eje X representa los días y el eje Y representa la demanda. Si tuviera que esperar varios meses entre recalibrar sus puntos de pedido, sin duda haría el pedido demasiado pronto. Al recalibrar su punto de reorden con mucha más frecuencia, captará el cambio en la demanda y permitirá pedidos mucho más precisos.

En lugar de esperar hasta que tenga un problema, vuelva a recalibrar todas las piezas en cada ciclo de planificación al menos una vez al mes. Al hacerlo, aprovecha los datos más recientes y ajusta proactivamente la política de almacenamiento, evitando así problemas que causarían revisiones manuales y escasez o exceso de inventario.

La naturaleza de sus datos (potencialmente variados) también debe combinarse con las herramientas de pronóstico adecuadas. Si los registros de algunas partes muestran tendencias o patrones estacionales, el uso de métodos de pronóstico de objetivos para adaptarse a estos patrones puede marcar una gran diferencia. De manera similar, si los datos muestran valores cero frecuentes (demanda intermitente), los métodos de pronóstico que no se basan en este caso especial pueden arrojar fácilmente resultados poco confiables.

Automatice, recalibre y revise las excepciones. El software especialmente diseñado lo hará automáticamente. Piénselo de otra manera: ¿es mejor depositar una gran cantidad de dinero en el inversiones una vez al año o en el "costo promedio en euros" depositando cantidades más pequeñas en que sector en el que decida invertir en fracciones mensuales? Recalibrar las políticas con regularidad generará rendimientos máximos con el tiempo, tal como lo hará el promedio del costo en euros para su cartera de inversiones.

¿Con qué frecuencia recalibra sus políticas de almacenamiento? ¿Por qué?

Este blog proporciona una descripción general de este tema escrito para no expertos. Eso

• explica por qué es posible que desee leer este blog.
• enumera los diversos tipos de "mantenimiento de la máquina".
• explica qué es el “modelado probabilístico”.
• describe modelos para predecir el tiempo de inactividad.
• explica lo que estos modelos pueden hacer por usted.

Importancia del tiempo de inactividad

Si fabrica cosas para la venta, necesita máquinas para hacer esas cosas. Si sus máquinas están en funcionamiento, tiene una gran oportunidad de ganar dinero. Si sus máquinas no funcionan, pierde oportunidades de ganar dinero. Dado que el tiempo de inactividad es tan fundamental, vale la pena invertir dinero y pensar en minimizar el tiempo de inactividad. Por pensamiento me refiero a matemáticas de probabilidad, ya que tiempo de inactividad de la máquina es inherentemente un fenómeno aleatorio. Modelos de probabilidad puede orientar las políticas de mantenimiento.

Políticas de mantenimiento de máquinas

El mantenimiento es su defensa contra el tiempo de inactividad. Existen varios tipos de políticas de mantenimiento, que van desde "No hacer nada y esperar a que falle" hasta enfoques analíticos sofisticados que involucran sensores y modelos de probabilidad de falla.

Una lista útil de políticas de mantenimiento es:

• Sentarse y esperar problemas, luego sentarse un poco más preguntándose qué hacer cuando los problemas inevitablemente suceden. Esto es tan tonto como suena.
• Igual que el anterior, excepto que se prepara para el fracaso de minimizar el tiempo de inactividad, por ejemplo, el almacenamiento de piezas de repuesto.
• Comprobación periódica de problemas inminentes junto con intervenciones como la lubricación de piezas móviles o la sustitución de piezas desgastadas.
• Basar la programación del mantenimiento en datos sobre el estado de la máquina en lugar de depender de un programa fijo; requiere la recopilación y el análisis continuos de datos. Esto se llama mantenimiento basado en la condición.
• Usar los datos sobre el estado de la máquina de forma más agresiva al convertirlos en predicciones de tiempo de falla y sugerencias de pasos a seguir para retrasar la falla. Esto se llama mantenimiento predictivo.

Los últimos tres tipos de mantenimiento se basan en matemáticas de probabilidad para establecer un programa de mantenimiento, o determinar cuándo los datos sobre el estado de la máquina requieren intervención, o calcular cuándo podría ocurrir una falla y cuál es la mejor manera de posponerla.

Modelos de probabilidad de falla de la máquina

El tiempo que una máquina funcionará antes de que falle es una variable aleatoria. Así es el tiempo que pasará abajo. La teoría de la probabilidad es la parte de las matemáticas que trata con variables aleatorias. Las variables aleatorias se describen por sus distribuciones de probabilidad, por ejemplo, ¿cuál es la probabilidad de que la máquina funcione durante 100 horas antes de que se apague? 200 horas? O, de manera equivalente, ¿cuál es la probabilidad de que la máquina siga funcionando después de 100 o 200 horas?

Un subcampo llamado "teoría de la confiabilidad" responde a este tipo de preguntas y aborda conceptos relacionados como el tiempo medio antes de la falla (MTBF), que es un resumen abreviado de la información codificada en la distribución de probabilidad del tiempo antes de la falla.

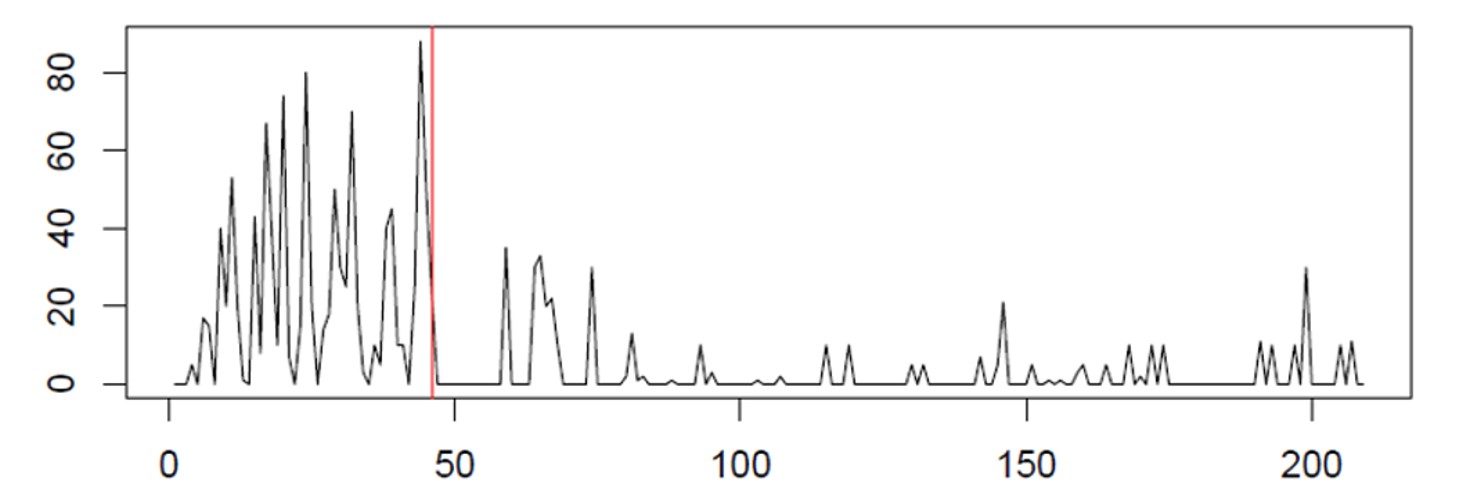
La Figura 1 muestra datos sobre el tiempo antes de la falla de las unidades de aire acondicionado. Este tipo de trama representa la distribución de probabilidad acumulada y muestra la posibilidad de que una unidad haya fallado después de que haya transcurrido cierto tiempo. La Figura 2 muestra un función de confiabilidad, trazando el mismo tipo de información en un formato inverso, es decir, representando la posibilidad de que una unidad siga funcionando después de que haya transcurrido cierto tiempo.

En la Figura 1, las marcas azules junto al eje x muestran los momentos en los que se observaron fallas en los acondicionadores de aire individuales; Estos son los datos básicos. La curva negra muestra la proporción acumulada de unidades que fallaron a lo largo del tiempo. La curva roja es una aproximación matemática a la curva negra, en este caso una distribución exponencial. Los gráficos muestran que alrededor del 80 por ciento de las unidades fallarán antes de las 100 horas de funcionamiento.

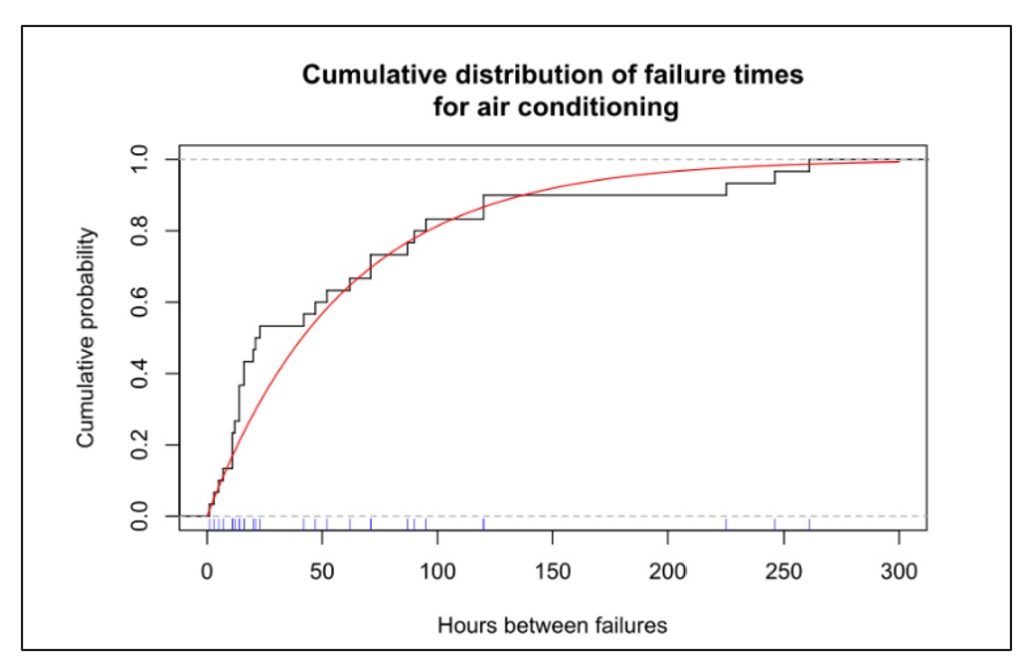
Figura 1 Función de distribución acumulativa del tiempo de actividad de los aires acondicionados

Los modelos de probabilidad se pueden aplicar a una pieza, componente o subsistema individual, a un conjunto de piezas relacionadas (p. ej., "el sistema hidráulico") oa una máquina completa. Cualquiera de estos puede describirse mediante la distribución de probabilidad del tiempo antes de que falle.

La Figura 2 muestra la función de confiabilidad de seis subsistemas en una máquina para excavar túneles. El gráfico muestra que el subsistema más fiable son los brazos de corte y el menos fiable es el subsistema de agua. La confiabilidad de todo el sistema podría aproximarse multiplicando las seis curvas (porque para que el sistema funcione como un todo, todos los subsistemas deben estar funcionando), lo que daría como resultado un intervalo muy corto antes de que algo salga mal.

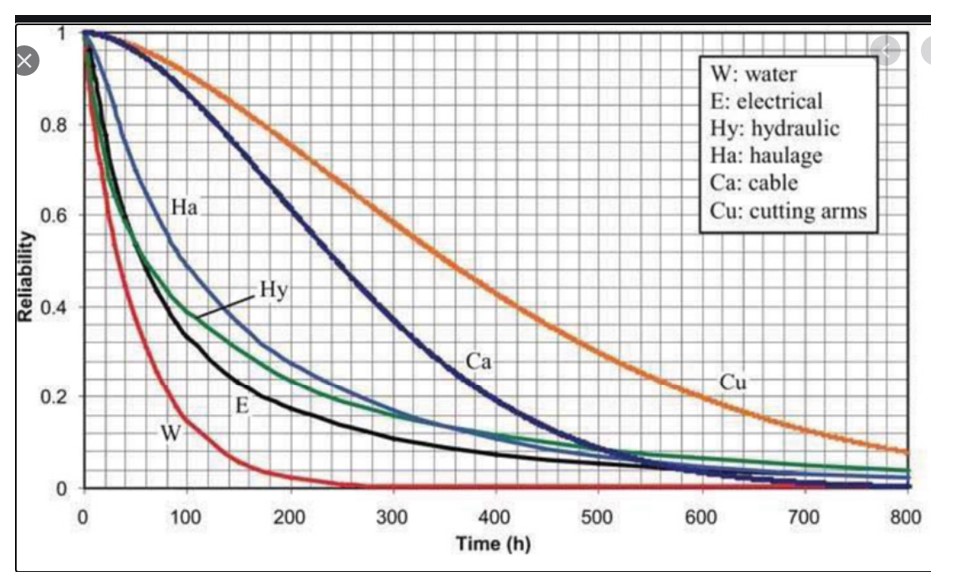
Figura 2 Ejemplos de distribuciones de probabilidad de subsistemas en una tuneladora

Varios factores influyen en la distribución del tiempo antes de la falla. Invertir en mejores piezas prolongará la vida útil del sistema. También lo hará la inversión en redundancia. Lo mismo ocurrirá con la sustitución de pars usados por nuevos.

Una vez que se dispone de una distribución de probabilidad, se puede utilizar para responder a cualquier cantidad de preguntas hipotéticas, como se ilustra a continuación en la sección Beneficios de los modelos.

Enfoques para modelar la confiabilidad de la máquina

Los modelos de probabilidad pueden describir las unidades más básicas, como componentes individuales del sistema (Figura 2), o conjuntos de unidades básicas, como máquinas completas (Figura 1). De hecho, una máquina completa se puede modelar como una sola unidad o como una colección de componentes. Si se trata una máquina completa como una sola unidad, la distribución de probabilidad de vida útil representa un resumen del efecto combinado de las distribuciones de vida útil de cada componente.

Si tenemos un modelo de una máquina completa, podemos saltar a modelos de colecciones de máquinas. Si, en cambio, comenzamos con modelos de la vida útil de los componentes individuales, de alguna manera debemos combinar esos modelos individuales en un modelo general de la máquina completa.

Aquí es donde las matemáticas pueden ponerse peludas. El modelado siempre requiere un equilibrio sabio entre la simplificación, para que algunos resultados sean posibles, y la complicación, para que cualquier resultado que surja sea realista. El truco habitual es asumir que las fallas de las piezas individuales del sistema ocurren de manera independiente.

Si podemos suponer que las fallas ocurren de manera independiente, generalmente es posible modelar colecciones de máquinas. Por ejemplo, suponga que una línea de producción tiene cuatro máquinas que producen el mismo producto. Tener un modelo de confiabilidad para una sola máquina (como en la Figura 1) nos permite predecir, por ejemplo, la posibilidad de que solo tres de las máquinas sigan funcionando dentro de una semana. Incluso aquí puede haber una complicación: la probabilidad de que una máquina que funciona hoy siga funcionando mañana a menudo depende de cuánto tiempo haya pasado desde su última falla. Si el tiempo entre fallas tiene una distribución exponencial como la de la Figura 1, resulta que el tiempo de la próxima falla no depende de cuánto tiempo ha pasado desde la última falla. Desafortunadamente, muchos o incluso la mayoría de los sistemas no tienen distribuciones exponenciales de tiempo de actividad, por lo que la complicación persiste.

Peor aún, si comenzamos con modelos de confiabilidad de muchos componentes individuales, avanzar hasta predecir los tiempos de falla para toda la máquina compleja puede ser casi imposible si tratamos de trabajar directamente con todas las ecuaciones relevantes. En tales casos, la única forma práctica de obtener resultados es utilizar otro estilo de modelado: la simulación Monte Carlo.

La simulación de Monte Carlo es una forma de sustituir la computación por el análisis cuando es posible crear escenarios aleatorios de operación del sistema. El uso de la simulación para extrapolar la confiabilidad de la máquina a partir de la confiabilidad de los componentes funciona de la siguiente manera.

1. Comience con las funciones de distribución acumulativa (Figura 1) o funciones de confiabilidad (Figura 2) de cada componente de la máquina.
2. Cree una muestra aleatoria de la vida útil de cada componente para obtener un conjunto de tiempos de falla de muestra consistentes con su función de confiabilidad.
3. Utilizando la lógica de cómo se relacionan los componentes entre sí, calcule el tiempo de falla de toda la máquina.
4. Repita los pasos 1 a 3 muchas veces para ver la gama completa de posibles vidas útiles de la máquina.
5. Opcionalmente, promedie los resultados del paso 4 para resumir la vida útil de la máquina con métricas como el MTBF o la posibilidad de que la máquina funcione más de 500 horas antes de fallar.

El paso 1 sería un poco complicado si no tenemos un buen modelo de probabilidad para la vida útil de un componente, por ejemplo, algo como la línea roja en la Figura 1.

El paso 2 puede requerir una contabilidad cuidadosa. A medida que avanza el tiempo en la simulación, algunos componentes fallarán y serán reemplazados, mientras que otros seguirán funcionando. A menos que la vida útil de un componente tenga una distribución exponencial, su vida útil restante dependerá de cuánto tiempo el componente haya estado en uso continuo. Así que este paso debe dar cuenta de los fenómenos de marcar a fuego o desgastar.

El paso 3 es diferente de los demás en que requiere algo de matemática básica, aunque de un tipo simple. Si la Máquina A solo funciona cuando los componentes 1 y 2 funcionan, entonces (suponiendo que la falla de un componente no influya en la falla del otro)

Probabilidad [A funciona] = Probabilidad [1 funciona] x Probabilidad [2 funciona].

Si, en cambio, la Máquina A funciona si el componente 1 funciona o el componente 2 funciona o ambos funcionan, entonces

Probabilidad [A falla] = Probabilidad [1 falla] x Probabilidad [2 fallas]

entonces Probabilidad [A funciona] = 1 – Probabilidad [A falla].

El paso 4 puede implicar la creación de miles de escenarios para mostrar la gama completa de resultados aleatorios. La computación es rápida y barata.

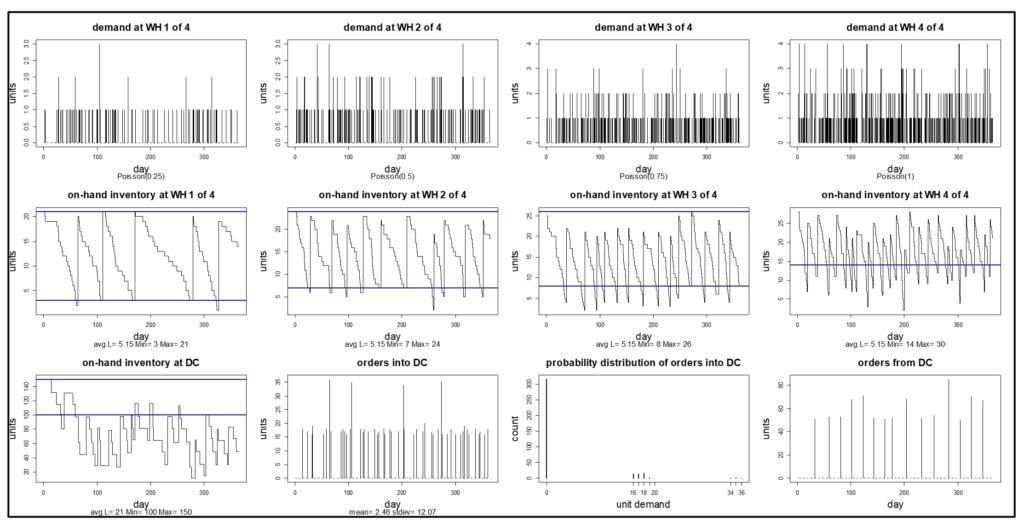
El paso 5 puede variar según los objetivos del usuario. Calcular el MTBF es estándar. Elija otros que se adapten al problema. Además de las estadísticas de resumen proporcionadas por el paso 5, se pueden trazar ejecuciones de simulación individuales para desarrollar la intuición sobre la dinámica aleatoria del tiempo de actividad y el tiempo de inactividad de la máquina. La Figura 3 muestra un ejemplo de una sola máquina que muestra ciclos alternos de tiempo de actividad y tiempo de inactividad que dan como resultado el tiempo de actividad del 85%.

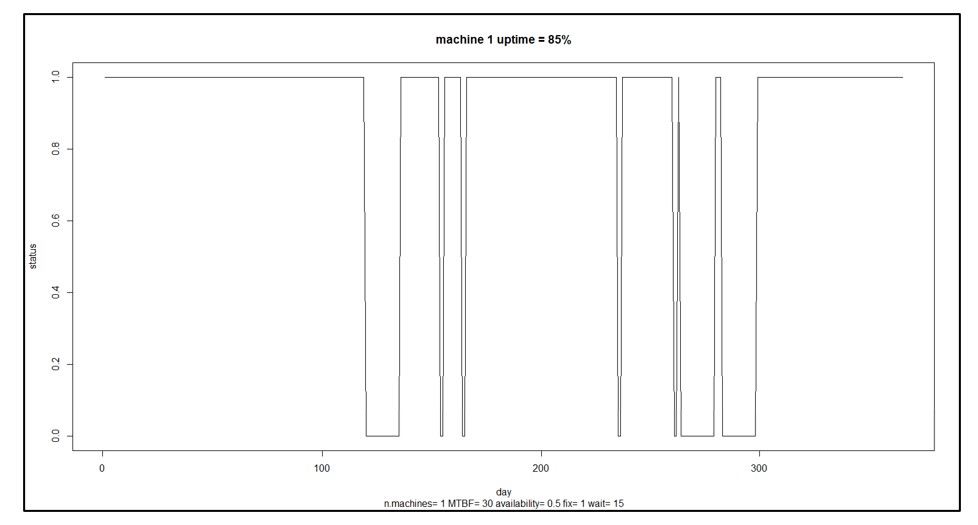
Figura 3 Un escenario de muestra para una sola máquina

Beneficios de los modelos de confiabilidad de la máquina

En la Figura 3, la máquina está funcionando 85% del tiempo. Eso puede no ser lo suficientemente bueno. Es posible que tenga algunas ideas sobre cómo mejorar la confiabilidad de la máquina, por ejemplo, tal vez pueda mejorar la confiabilidad del componente 3 comprando una versión mejor y más nueva de un proveedor diferente. ¿Cuánto ayudaría eso? Eso es difícil de adivinar: el componente 3 puede ser solo uno de varios y quizás no el eslabón más débil, y cuánto vale el cambio depende de qué tan mejor sea el nuevo. Tal vez debería desarrollar una especificación para el componente 3 que luego pueda comprar a proveedores potenciales, pero ¿cuánto tiempo tiene que durar el componente 3 para tener un impacto material en el MTBF de la máquina?

Aquí es donde vale la pena tener un modelo. Sin un modelo, estás confiando en conjeturas. Con un modelo, puede convertir la especulación sobre situaciones hipotéticas en estimaciones precisas. Por ejemplo, podría analizar cómo un aumento de 10% en MTBF para el componente 3 se traduciría en una mejora en MTBF para toda la máquina.

Como otro ejemplo, suponga que tiene siete máquinas que producen un producto importante. Calcula que debe dedicar seis de las siete para cumplir con un pedido importante de su gran cliente, dejando una máquina para manejar la demanda de una cantidad de clientes pequeños misceláneos y para servir como repuesto. Se podría usar un modelo de confiabilidad para cada máquina para estimar las probabilidades de varias contingencias: las siete máquinas funcionan y la vida es buena; seis máquinas funcionan para que al menos puedas mantener contento a tu cliente clave; solo funcionan cinco máquinas, así que tienes que negociar algo con tu cliente clave, etc.

En resumen, los modelos de probabilidad de fallas de máquinas o componentes pueden proporcionar la base para convertir los datos de tiempo de falla en decisiones comerciales inteligentes.

Leer más sobre  Maximice el tiempo de actividad de la máquina con el modelado probabilístico

Leer más sobre   Pronóstico probabilístico para demanda intermitente

Administrar el inventario en una sola instalación es bastante difícil, pero el problema se vuelve mucho más complejo cuando hay múltiples instalaciones dispuestas en múltiples escalones. La complejidad surge de las interacciones entre los escalones, con demandas en los niveles más bajos que aumentan y cualquier escasez en los niveles más altos se reduce en cascada.

Si cada una de las instalaciones se administrara de forma aislada, se podrían usar métodos estándar, sin tener en cuenta las interacciones, para establecer parámetros de control de inventario, como puntos de pedido y cantidades de pedido. Sin embargo, ignorar las interacciones entre niveles puede conducir a fallas catastróficas. La experiencia y el ensayo y error permiten el diseño de sistemas estables, pero esa estabilidad puede verse afectada por cambios en los patrones de demanda o tiempos de entrega o por la adición de nuevas instalaciones. El análisis avanzado de la cadena de suministro ayuda en gran medida a hacer frente a tales cambios, lo que proporciona un "sandbox" seguro dentro del cual probar los cambios propuestos en el sistema antes de implementarlos. Este blog ilustra ese punto.

El escenario

Para tener alguna esperanza de discutir este problema de manera útil, este blog simplificará el problema al considerar la jerarquía de dos niveles que se muestra en la Figura 1. Imagine que las instalaciones en el nivel inferior son almacenes (WH) desde los cuales se pretende satisfacer las demandas de los clientes. , y que los artículos de inventario en cada WH son piezas de servicio que se venden a una amplia gama de clientes externos.

Figura 1: Estructura general de un tipo de sistema de inventario de dos niveles

Imagine que el nivel superior consiste en un único centro de distribución (DC) que no atiende a los clientes directamente pero sí reabastece los WH. Para simplificar, suponga que el centro de distribución en sí se reabastece desde una fuente que siempre tiene (o produce) existencias suficientes para enviar inmediatamente las piezas al centro de distribución, aunque con cierto retraso. (Alternativamente, podríamos considerar que el sistema tiene tiendas minoristas abastecidas por un almacén).

Cada nivel se puede describir en términos de niveles de demanda (tratados como aleatorios), plazos de entrega (aleatorios), parámetros de control de inventario (aquí, valores mínimos y máximos) y política de escasez (aquí, se permiten pedidos pendientes).

El método de análisis

La literatura académica ha avanzado en este problema, aunque generalmente a costa de simplificaciones necesarias para facilitar una solución puramente matemática. Nuestro enfoque aquí es más accesible y flexible: simulación Monte Carlo. Es decir, construimos un programa informático que incorpora la lógica de funcionamiento del sistema. El programa “crea” una demanda aleatoria en el nivel de WH, procesa la demanda de acuerdo con la lógica de una política de inventario elegida y crea demanda para el CD agrupando las solicitudes aleatorias de reposición realizadas por los WH. Este enfoque nos permite observar muchos días simulados de operación del sistema mientras observamos eventos significativos como desabastecimientos en cualquier nivel.

Un ejemplo

Para ilustrar un análisis, simulamos un sistema que consta de cuatro WH y un DC. La demanda promedio varió entre los WH. La reposición del CD a cualquier WH tomó de 4 a 7 días, con un promedio de 5,15 días. La reposición de la CC desde la Fuente tomó 7, 14, 21 o 28 días, pero 90% del tiempo fue 21 o 28 días, lo que hace un promedio de 21 días. Cada instalación tenía valores mínimos y máximos establecidos por el criterio del analista después de algunos cálculos aproximados.

La Figura 2 muestra los resultados de un año de operación diaria simulada de este sistema. La primera fila de la figura muestra la demanda diaria del artículo en cada WH, que se supuso que era "puramente aleatoria", lo que significa que tenía una distribución de Poisson. La segunda fila muestra el inventario disponible al final de cada día, con los valores mínimo y máximo indicados por líneas azules. La tercera fila describe las operaciones en el CD. Contrariamente a la suposición de gran parte de la teoría, la demanda en el DC no estaba cerca de ser Poisson, ni tampoco la demanda fuera del DC a la Fuente. En este escenario, los valores Mín. y Máx. fueron suficientes para mantener alta la disponibilidad de artículos en cada WH y en el CD, y no se observaron desabastecimientos en ninguna de las cinco instalaciones.

Click aquí para ampliar la imagen

Figura 2 – Año de operación simulado de un sistema con cuatro WHs y un DC.

Ahora vamos a variar el escenario. Cuando los desabastecimientos son extremadamente raros, como en la Figura 2, a menudo hay un exceso de inventario en el sistema. Supongamos que alguien sugiere que el nivel de inventario en el centro de distribución parece un poco alto y piensa que sería una buena idea ahorrar dinero allí. Su sugerencia para reducir las existencias en el CD es reducir el valor de Min en el CD de 100 a 50. ¿Qué sucede? Podrías adivinar, o podrías simular.

La figura 3 muestra la simulación: el resultado no es agradable. El sistema funciona bien durante gran parte del año, luego el centro de distribución se queda sin existencias y no puede ponerse al día a pesar de enviar órdenes de reposición cada vez mayores a la fuente. Tres de los cuatro WH descienden en espirales de muerte al final del año (y WH1 sigue a partir de entonces). La simulación ha puesto de relieve una sensibilidad que no se puede ignorar y ha marcado una mala decisión.

Haga click aquí para ampliar la imágen

Figura 3: efectos simulados de reducir el Min en el DC.

Ahora los gerentes de inventario pueden volver a la mesa de diseño y probar otras formas posibles de reducir la inversión en inventario a nivel de CD. Un movimiento que siempre ayuda, si usted y su proveedor pueden lograrlo juntos, es crear un sistema más ágil al reducir el tiempo de reabastecimiento. Trabajar con la fuente para garantizar que el centro de distribución siempre obtenga sus reabastecimientos en 7 o 14 días estabiliza el sistema, como se muestra en la Figura 4.

Haga click aquí para ampliar la imágen

Figura 4: efectos simulados de reducir el tiempo de espera para reponer el centro de distribución.

Desafortunadamente, no se ha logrado la intención de reducir el inventario en el DC. El recuento de inventario diario original era de unas 80 unidades y sigue siendo de unas 80 unidades después de reducir el mínimo del centro de distribución y mejorar drásticamente el tiempo de entrega de la fuente al centro de distribución. Pero con el modelo de simulación, el equipo de planificación puede probar otras ideas hasta llegar a un rediseño satisfactorio. O, dado que la Figura 4 muestra que el inventario de CD comienza a coquetear con cero, podrían pensar que es prudente aceptar la necesidad de un promedio de aproximadamente 80 unidades en el CD y buscar formas de recortar la inversión en inventario en los WH.

la comida para llevar

1. La optimización de inventario de varios niveles (MEIO) es compleja. Muchos factores interactúan para producir comportamientos del sistema que pueden resultar sorprendentes incluso en sistemas simples de dos niveles.
2. La simulación de Monte Carlo es una herramienta útil para los planificadores que necesitan diseñar nuevos sistemas o modificar los existentes.