Als je op de hoogte blijft van het nieuws over supply chain-analyse, u komt vaker de uitdrukking "probabilistische prognoses" tegen. Als deze zin raadselachtig is, lees dan verder.
U weet waarschijnlijk al wat 'voorspelling' betekent. En je weet waarschijnlijk ook dat er veel verschillende manieren lijken te zijn om het te doen. En je hebt waarschijnlijk scherpe kleine zinnen gehoord als 'elke voorspelling is verkeerd'. Dus je weet dat een soort van wiskundige zou kunnen berekenen dat "de voorspelling is dat u volgende maand 100 eenheden zult verkopen", en dan zou u 110 eenheden kunnen verkopen, in welk geval u een 10%-voorspellingsfout heeft.
Je weet misschien niet dat wat ik zojuist heb beschreven een bepaald soort voorspelling is, een 'puntvoorspelling'. Een puntenvoorspelling wordt zo genoemd omdat deze uit slechts een enkel getal bestaat (dwz één punt op de getallenlijn, als je je de getallenlijn herinnert uit je jeugd).
Punt voorspellingen hebben één deugd: ze zijn eenvoudig. Ze hebben ook een fout: ze geven aanleiding tot snauwende uitspraken als 'elke voorspelling is verkeerd'. Dat wil zeggen, in de meeste realistische gevallen is het onwaarschijnlijk dat de werkelijke waarde exact gelijk zal zijn aan de voorspelling. (Wat niet zo erg is als de voorspelling dichtbij genoeg is.)
Dit brengt ons bij 'probabilistische voorspellingen'. Deze aanpak is een stap verder, want in plaats van een voorspelling met één cijfer (punt) te produceren, levert het een kansverdeling op voor de voorspelling. En in tegenstelling tot traditionele extrapolatieve modellen die puur op historische gegevens vertrouwen, hebben probabilistische voorspellingen de mogelijkheid om toekomstige waarden te simuleren die niet verankerd zijn in het verleden.
"Waarschijnlijkheidsverdeling" is een verbiedende uitdrukking, die wat mysterieuze wiskunde oproept waar je misschien van hebt gehoord maar nooit hebt bestudeerd. Gelukkig hebben de meeste volwassenen genoeg levenservaring om het concept intuïtief te begrijpen. Wanneer afgebroken, is het vrij eenvoudig te begrijpen.
Stel je de simpele handeling voor van het opgooien van twee munten. Je zou dit onschuldig plezier kunnen noemen, maar ik noem het een 'probabilistisch experiment'. Het totale aantal kop dat op de twee munten verschijnt, is nul, één of twee. Het opgooien van twee munten is een 'willekeurig experiment'. Het resulterende aantal koppen is een "willekeurige variabele". Het heeft een "kansverdeling", wat niets meer is dan een tabel van hoe waarschijnlijk het is dat de willekeurige variabele een van zijn mogelijke waarden zal blijken te hebben. De kans om twee kop te krijgen als de munten eerlijk zijn, is ¼, net als de kans op geen kop. De kans op één kop is ½.
Dezelfde benadering kan een interessantere willekeurige variabele beschrijven, zoals de dagelijkse vraag naar een reserveonderdeel. Figuur 2 toont een dergelijke kansverdeling. Het werd berekend door drie jaar dagelijkse vraaggegevens te verzamelen over een bepaald onderdeel dat wordt gebruikt in een wetenschappelijk instrument dat aan ziekenhuizen wordt verkocht.
Figuur 1: De kansverdeling van de dagelijkse vraag naar een bepaald reserveonderdeel
De verdeling in figuur 1 kan worden gezien als een probabilistische voorspelling van de vraag op één dag. Voor dit specifieke onderdeel zien we dat de voorspelling zeer waarschijnlijk nul zal zijn (97% kans), maar soms voor een handvol eenheden, en eens in de drie jaar twintig eenheden. Hoewel de meest waarschijnlijke voorspelling nul is, zou je er een paar bij de hand willen houden als dit onderdeel van cruciaal belang zou zijn ("... bij gebrek aan een spijker ...")
Laten we deze informatie nu gebruiken om een meer gecompliceerde probabilistische voorspelling te maken. Stel dat je drie eenheden bij de hand hebt. Hoeveel dagen duurt het voordat je er geen hebt? Er zijn veel mogelijke antwoorden, variërend van een enkele dag (als u onmiddellijk een vraag krijgt voor drie of meer) tot een zeer groot aantal (aangezien 97% dagen geen vraag ziet). De analyse van deze vraag is een beetje ingewikkeld vanwege de vele manieren waarop deze situatie zich kan voordoen, maar het uiteindelijke antwoord dat het meest informatief is, is een kansverdeling. Het blijkt dat het aantal dagen totdat er geen eenheden meer in voorraad zijn de verdeling heeft zoals weergegeven in figuur 2.
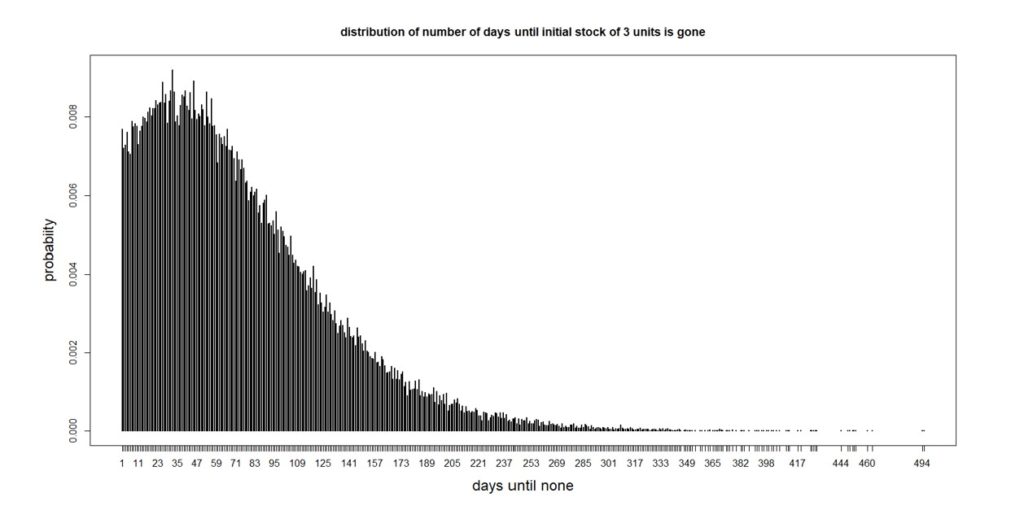
Figuur 2: Verdeling van het aantal dagen totdat alle drie de units op zijn
Het gemiddelde aantal dagen is 74, wat een puntvoorspelling zou zijn, maar er is veel variatie rond het gemiddelde. Vanuit het perspectief van voorraadbeheer valt op dat er een kans van 25% is dat alle units na 32 dagen op zijn. Dus als u besluit om meer te bestellen terwijl er nog maar drie in het schap liggen, zou het goed zijn als de leverancier ze u bezorgt voordat er een maand is verstreken. Als ze dat niet konden, zou je een kans van 75% hebben om de voorraad op te slaan - niet goed voor een cruciaal onderdeel.
De analyse achter figuur 2 omvatte het maken van enkele aannames die handig waren, maar niet nodig als ze niet waar waren. De resultaten kwamen van een methode genaamd "Monte Carlo-simulatie", waarin we beginnen met drie eenheden, een willekeurige vraag kiezen uit de verdeling in figuur 1, deze aftrekken van de huidige voorraad en doorgaan totdat de voorraad op is, waarbij wordt geregistreerd hoeveel dagen gingen voorbij voordat je op was. Herhaling van dit proces 100.000 keer geproduceerd Figuur 2.
Toepassingen van Monte Carlo-simulatie strekken zich uit tot problemen met een nog grotere reikwijdte dan het bovenstaande voorbeeld "wanneer zijn we op". Vooral belangrijk zijn Monte Carlo-voorspellingen van de toekomstige vraag. Hoewel het gebruikelijke voorspellingsresultaat een reeks puntvoorspellingen is (bijvoorbeeld de verwachte vraag per eenheid in de komende twaalf maanden), weten we dat er een aantal manieren zijn waarop de werkelijke vraag zich zou kunnen voordoen. Simulatie zou kunnen worden gebruikt om bijvoorbeeld duizend mogelijke sets van 365 dagelijkse vraagbehoeften te produceren.
Deze reeks vraagscenario's zou het scala aan mogelijke situaties waarmee een voorraadsysteem het hoofd zou moeten bieden, vollediger blootleggen. Dit gebruik van simulatie wordt "stresstesten" genoemd, omdat het een systeem blootstelt aan een reeks gevarieerde maar realistische scenario's, waaronder enkele vervelende. Die scenario's worden vervolgens ingevoerd in wiskundige modellen van het systeem om te zien hoe goed het zal omgaan, zoals weerspiegeld in key performance indicators (KPI's). Hoeveel stockouts zijn er bijvoorbeeld in die duizend gesimuleerde jaren van werking in het slechtste jaar? het gemiddelde jaar? het beste jaar? Wat is in feite de volledige kansverdeling van het aantal stockouts in een jaar, en wat is de verdeling van hun omvang?
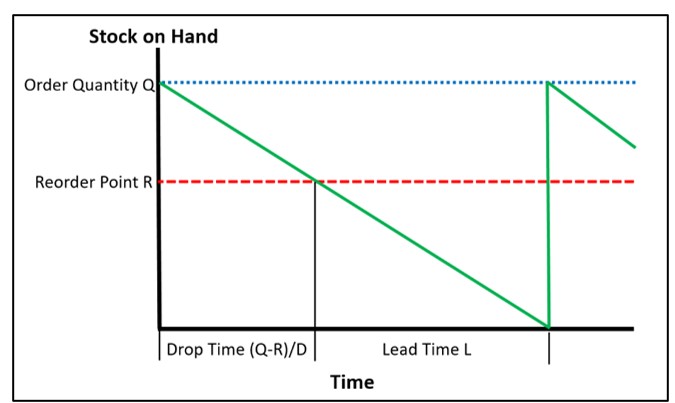
Figuren 3 en 4 illustreren probabilistische modellering van een voorraadbeheersysteem dat stockouts omzet in backorders. Het gesimuleerde systeem gebruikt een Min/Max-regelbeleid met Min = 10 eenheden en Max = 20 eenheden.
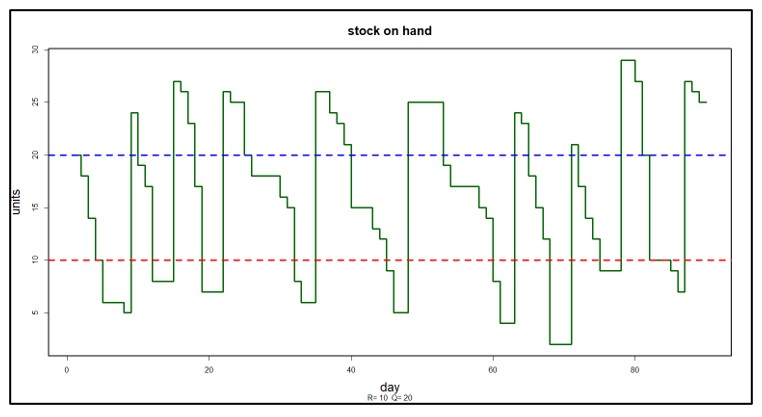
Figuur 3 toont een gesimuleerd jaar van dagelijkse operaties in vier plots. De eerste grafiek toont een bepaald patroon van willekeurige dagelijkse vraag waarin de gemiddelde vraag gestaag toeneemt van maandag tot vrijdag, maar in het weekend verdwijnt. De tweede grafiek toont het aantal eenheden dat elke dag voorhanden is. Merk op dat er tijdens dit gesimuleerde jaar een tiental keren is dat de voorraad negatief wordt, wat wijst op stockouts. De derde grafiek toont de omvang en timing van aanvullingsorders. De vierde grafiek toont de omvang en timing van backorders. De informatie in deze plots kan worden vertaald in schattingen van voorraadinvesteringen, gemiddelde eenheden voorhanden, houdkosten, bestelkosten en tekortkosten.
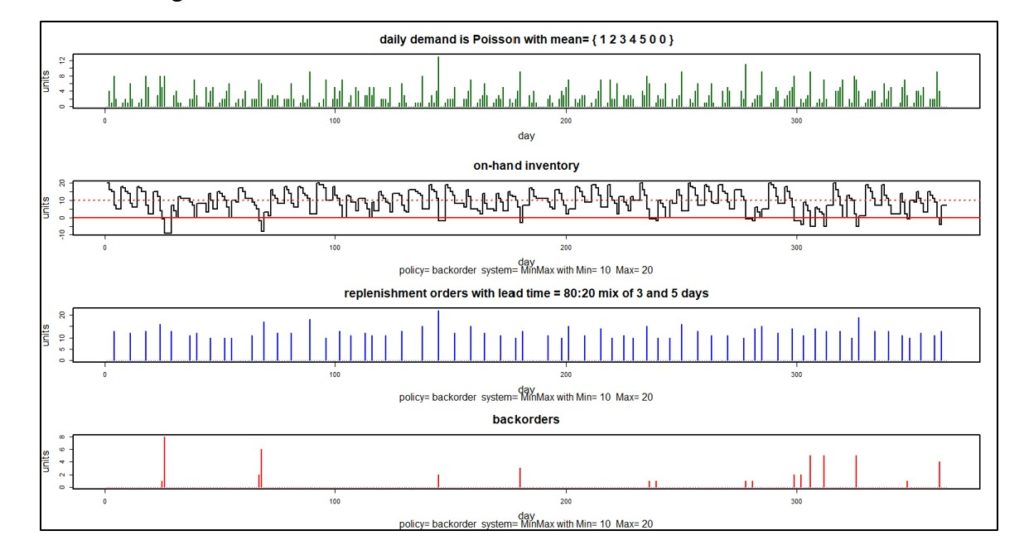
Figuur 3: Een gesimuleerd jaar van werking van het voorraadsysteem
Figuur 3 toont één van duizend gesimuleerde jaren. Elk jaar zal verschillende dagelijkse eisen hebben, wat resulteert in verschillende waarden van statistieken, zoals beschikbare eenheden en de verschillende componenten van de bedrijfskosten. Figuur 4 geeft de verdeling weer van 1.000 gesimuleerde waarden van vier KPI's. Door 1000 jaar ingebeelde werking te simuleren, wordt het bereik van mogelijke resultaten blootgelegd, zodat planners niet alleen rekening kunnen houden met gemiddelde resultaten, maar ook de best-case en worst-case-waarden kunnen zien.
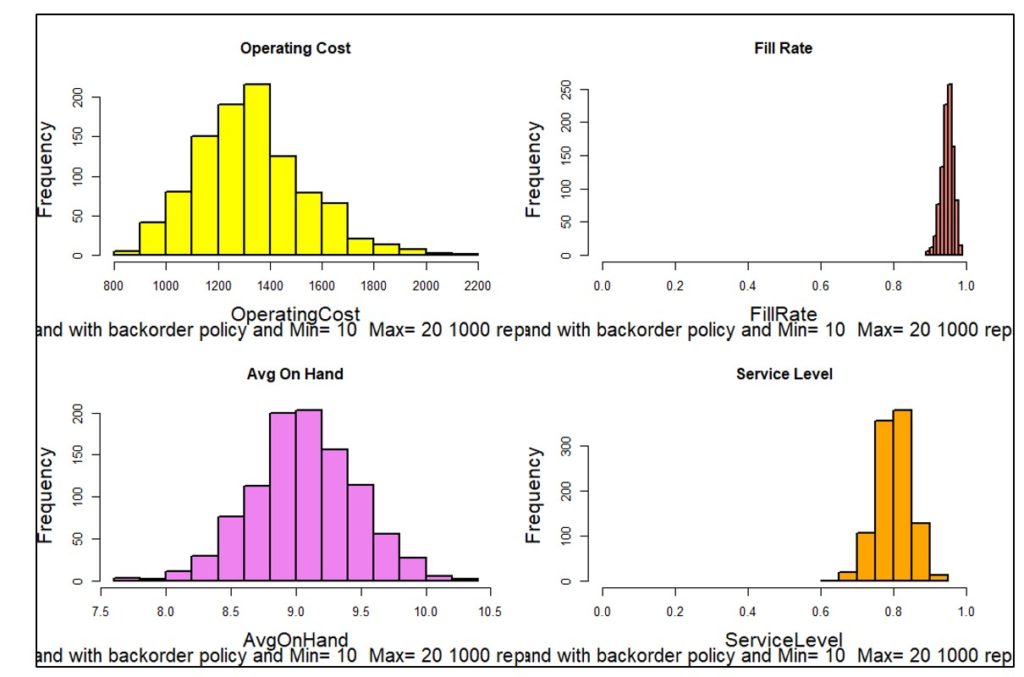
Figuur 4: Verdelingen van vier KPI's op basis van 1.000 simulaties
Monte Carlo-simulatie is een benadering met weinig wiskunde en hoge resultaten voor probabilistische prognoses: zeer praktisch en gemakkelijk uit te leggen. Geavanceerde probabilistische voorspellingsmethoden die door Smart Software worden gebruikt, breiden uit op de standaard Monte Carlo-simulatie en leveren uiterst nauwkeurige schattingen van de vereiste voorraadniveaus op.
gerelateerde berichten
Undershoot saboteert uw serviceniveau!
Undershoot betekent dat de doorlooptijd niet begint op het bestelpunt, maar eronder. Onderschrijding gebeurt elke keer dat de vraag die het bestelpunt overschreed, de voorraad onder (niet tot) het bestelpunt deed dalen. Undershoot pakt uw zak voordat u zelfs maar begint met het gooien van de dobbelstenen. Het misleidt de voorraadprofessional door te denken dat zijn of haar bestelpunten voldoende zijn om hun doelen te bereiken, terwijl de werkelijke prestaties niet voldoende zijn.
Hoe u een doelserviceniveau kiest
Houd bij het instellen van een doelserviceniveau rekening met factoren zoals huidige serviceniveaus, doorlooptijden voor aanvullingen, kostenbeperkingen, de pijn die wordt veroorzaakt door tekorten voor u en uw klanten, en uw concurrentiepositie.
Onthul uw werkelijke voorraadplanning en prognosebeleid door deze 10 vragen te beantwoorden
In deze blog bespreken we 10 specifieke vragen die u kunt stellen om te ontdekken wat er werkelijk gebeurt met het voorraadplanning- en vraagprognosebeleid in uw bedrijf. We beschrijven de typische antwoorden die worden gegeven wanneer een prognose-/inventarisplanningsbeleid niet echt bestaat, leggen uit hoe deze antwoorden moeten worden geïnterpreteerd en geven duidelijk advies over wat u eraan kunt doen.
recente berichten
Het beheren van de voorraad reserveonderdelen: beste praktijkenIn this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
5 manieren om de snelheid van beslissingen in de toeleveringsketen te verbeterenDe belofte van een digitale supply chain heeft de manier waarop bedrijven opereren getransformeerd. In de kern kan het snelle, datagestuurde beslissingen nemen en tegelijkertijd kwaliteit en efficiëntie in de hele bedrijfsvoering garanderen. Het gaat echter niet alleen om toegang tot meer data. Organisaties hebben de juiste tools en platforms nodig om die data om te zetten in bruikbare inzichten. Dit is waar besluitvorming cruciaal wordt, vooral in een landschap waar nieuwe digitale supply chain-oplossingen en AI-gestuurde platforms u kunnen ondersteunen bij het stroomlijnen van veel processen binnen de beslissingsmatrix. […]
12 Oorzaken van Overstocking en Praktische OplossingenEffectief voorraadbeheer is cruciaal voor het behouden van een gezonde balans en het verzekeren dat middelen optimaal worden toegewezen. Hier is een diepgaande verkenning van de belangrijkste oorzaken van overstocking, hun implicaties en mogelijke oplossingen. […]
FAQ: Slimme IP&O voor beter voorraadbeheer.Effectief supply chain- en voorraadbeheer zijn essentieel voor het bereiken van operationele efficiëntie en klanttevredenheid. Deze blog biedt duidelijke en beknopte antwoorden op enkele basisvragen en andere veelvoorkomende vragen van onze Smart IP&O-klanten, en biedt praktische inzichten om typische uitdagingen te overwinnen en uw voorraadbeheerpraktijken te verbeteren. Met de focus op deze belangrijke gebieden helpen we u complexe voorraadproblemen om te zetten in strategische, beheersbare acties die kosten verlagen en de algehele prestaties verbeteren met Smart IP&O. […]
7 belangrijke trends in vraagplanning die de toekomst vormgevenVraagplanning gaat verder dan alleen het voorspellen van productbehoeften; het gaat erom ervoor te zorgen dat uw bedrijf nauwkeurig, efficiënt en kosteneffectief aan de vraag van klanten voldoet. De nieuwste technologie voor vraagplanning pakt belangrijke uitdagingen aan, zoals nauwkeurigheid van voorspellingen, voorraadbeheer en marktresponsiviteit. In deze blog introduceren we kritieke trends voor vraagplanning, waaronder datagestuurde inzichten, probabilistische voorspellingen, consensusplanning, voorspellende analyses, scenariomodellering, realtime zichtbaarheid en multilevel voorspellingen. Deze trends helpen u om voorop te blijven lopen, uw toeleveringsketen te optimaliseren, kosten te verlagen en de klanttevredenheid te verbeteren, waardoor uw bedrijf op de lange termijn succesvol wordt. […]
Voorraadoptimalisatie voor fabrikanten, distributeurs en MRO
- Het beheren van de voorraad reserveonderdelen: beste praktijkenIn this blog, we’ll explore several effective strategies for managing spare parts inventory, emphasizing the importance of optimizing stock levels, maintaining service levels, and using smart tools to aid in decision-making. Managing spare parts inventory is a critical component for businesses that depend on equipment uptime and service reliability. Unlike regular inventory items, spare parts often have unpredictable demand patterns, making them more challenging to manage effectively. An efficient spare parts inventory management system helps prevent stockouts that can lead to operational downtime and costly delays while also avoiding overstocking that unnecessarily ties up capital and increases holding costs. […]
Innovatie van de OEM-aftermarket met AI-gestuurde voorraadoptimalisatieDe aftermarketsector biedt OEM's een beslissend voordeel door een stabiele inkomstenstroom te bieden en de loyaliteit van klanten te bevorderen door de betrouwbare en tijdige levering van serviceonderdelen. Het beheren van inventaris en het voorspellen van de vraag in de aftermarket gaat echter gepaard met uitdagingen, waaronder onvoorspelbare vraagpatronen, enorme productassortimenten en de noodzaak van snelle doorlooptijden. Traditionele methoden schieten vaak tekort vanwege de complexiteit en variabiliteit van de vraag in de aftermarket. De nieuwste technologieën kunnen grote datasets analyseren om de toekomstige vraag nauwkeuriger te voorspellen en voorraadniveaus te optimaliseren, wat leidt tot betere service en lagere kosten. […]
Toekomstbestendige hulpprogramma's: geavanceerde analyses voor optimalisatie van de supply chainNutsvoorzieningen op het gebied van elektriciteit, aardgas, stedelijk water en telecommunicatie zijn allemaal activa-intensief en afhankelijk van fysieke infrastructuur die in de loop van de tijd goed moet worden onderhouden, bijgewerkt en geüpgraded. Het maximaliseren van de uptime van bedrijfsmiddelen en de betrouwbaarheid van de fysieke infrastructuur vereist effectief voorraadbeheer, prognoses van reserveonderdelen en leveranciersbeheer. Een nutsbedrijf dat deze processen effectief uitvoert, presteert beter dan zijn concurrenten, levert een beter rendement op voor zijn investeerders en hogere serviceniveaus voor zijn klanten, terwijl het zijn impact op het milieu vermindert. […]
Centreringswet: timing, prijzen en betrouwbaarheid van reserveonderdelenIn dit artikel begeleiden we u bij het opstellen van een voorraadplan voor reserveonderdelen, waarbij prioriteit wordt gegeven aan beschikbaarheidsstatistieken zoals serviceniveaus en vulpercentages, terwijl de kostenefficiëntie wordt gewaarborgd. We zullen ons concentreren op een benadering van voorraadplanning genaamd Service Level-Driven Inventory Optimization. Vervolgens bespreken we hoe u kunt bepalen welke onderdelen u in uw inventaris moet opnemen en welke onderdelen mogelijk niet nodig zijn. Ten slotte onderzoeken we manieren om uw op serviceniveau gebaseerde voorraadplan consistent te verbeteren. […]
