Dos problemas de inventario
Si fabricas y vendes cosas, tienes dos problemas de inventario. Las empresas que venden cosas deben concentrarse incansablemente en tener suficiente inventario de productos para satisfacer la demanda de los clientes. Los fabricantes y las industrias intensivas en activos, como la generación de energía, el transporte público, la minería y la refinación, tienen una preocupación de inventario adicional: tener suficientes repuestos para mantener sus máquinas en funcionamiento. Este resumen técnico revisa los conceptos básicos de dos modelos probabilísticos de avería de la máquina. También relaciona el tiempo de actividad de la máquina con la adecuación del inventario de piezas de repuesto.
Modelización del fallo de una máquina tratada como una “caja negra”
Así como la demanda de productos es inherentemente aleatoria, también lo es el momento de las averías de las máquinas. Del mismo modo, así como el modelado probabilístico es la forma correcta de lidiar con la demanda aleatoria, también es la forma correcta de lidiar con fallas aleatorias.
Los modelos de avería de máquinas tienen dos componentes. El primero se ocupa de la duración aleatoria del tiempo de actividad. El segundo se ocupa de la duración aleatoria del tiempo de inactividad.
El campo de teoría de la confiabilidad ofrece varios modelos de probabilidad estándar que describen el tiempo aleatorio hasta la falla de una máquina sin tener en cuenta el motivo de la falla. El modelo más simple de tiempo de actividad es el distribución exponencial. Este modelo dice que el tasa de riesgo, es decir, la posibilidad de fallar en el siguiente instante de tiempo es constante sin importar cuánto tiempo haya estado operando el sistema. El modelo exponencial hace un buen trabajo modelando ciertos tipos de sistemas, especialmente electrónicos, pero no es universalmente aplicable.
Descargar el documento técnico
El siguiente paso en la complejidad del modelo es el Weibull modelo (pronunciado “POR QUÉ-toro”). La distribución de Weibull permite que el riesgo de falla cambie con el tiempo, ya sea disminuyendo después de un período de quemado o, más a menudo, aumentando a medida que se acumula el desgaste. La distribución exponencial es un caso especial de la distribución de Weibull en la que la tasa de riesgo no aumenta ni disminuye.
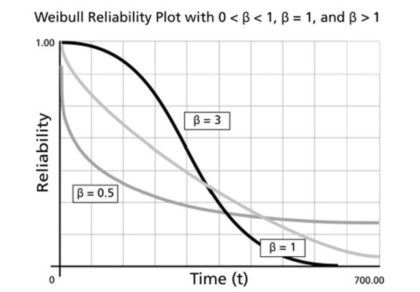
Figura 1: Tres curvas de supervivencia de Weibull diferentes
La Figura 1 ilustra la probabilidad del modelo de Weibull de que una máquina aún esté funcionando como una función de cuánto tiempo ha estado funcionando. Hay tres curvas correspondientes a tasas de riesgo constantes, decrecientes y crecientes. Por razones obvias, estos se llaman curvas de supervivencia porque grafican la probabilidad de sobrevivir por varias cantidades de tiempo (pero también se les llama curvas de confiabilidad). La curva negra que comienza alta y desciende rápidamente (β=3) representa una máquina que se desgasta con el tiempo. La curva más ligera en el medio rápido (β=1) muestra la distribución exponencial. La curva media-oscura (β=0.5) es aquella que tiene una alta tasa de riesgo temprano pero mejora con la edad.
Por supuesto, hay otro fenómeno que debe incluirse en el análisis: el tiempo de inactividad. Modelar el tiempo de inactividad es donde la teoría del inventario entra en escena. El tiempo de inactividad se modela mediante una mezcla de dos distribuciones diferentes. Si hay una pieza de repuesto disponible para reemplazar la pieza defectuosa, el tiempo de inactividad puede ser muy breve, digamos un día. Pero si no hay repuestos en stock, el tiempo de inactividad puede ser bastante largo. Incluso si el repuesto se puede obtener rápidamente, pueden pasar varios días o una semana antes de que se pueda reparar la máquina. Si el repuesto debe ser fabricado por un proveedor lejano y enviado por mar, luego por tren y luego por camión a su planta, el tiempo de inactividad podría ser de semanas o meses. Todo esto significa que mantener un inventario adecuado de repuestos es muy importante para mantener la producción en marcha.
En este tipo de análisis agregado, la máquina se trata como una caja negra que funciona o no. Aunque ignora los detalles de qué parte falló y cuándo, dicho modelo es útil para dimensionar el grupo de máquinas necesarias para mantener un nivel mínimo de capacidad de producción con alta probabilidad.
Él Distribución binomial es el modelo de probabilidad relevante para este problema. El binomio es el mismo modelo que describe, por ejemplo, la distribución del número de “caras” resultantes de veinte lanzamientos de una moneda. En el problema de confiabilidad de las máquinas, las máquinas corresponden a monedas, y un resultado de caras corresponde a tener una máquina en funcionamiento.
Como ejemplo, si
- la posibilidad de que cualquier máquina esté funcionando en un día en particular es 90%
- las fallas de las máquinas son independientes (p. ej., no hay inundaciones ni tornados que las eliminen todas a la vez)
- necesita al menos una probabilidad de 95% de que al menos 5 máquinas estén funcionando en un día determinado
luego, el modelo binomial prescribe siete máquinas para lograr su objetivo.
Modelado de fallas de máquinas basadas en fallas de componentes

El modelo de Weibull también se puede usar para describir la falla de una sola pieza. Sin embargo, cualquier máquina de producción realistamente compleja tendrá múltiples partes y, por lo tanto, tendrá múltiples modos de falla. Esto significa que calcular el tiempo hasta que la máquina falla requiere el análisis de una “carrera hacia la falla”, con cada parte compitiendo por el “honor” de ser la primera en fallar.
Si hacemos la suposición razonable de que las piezas fallan de forma independiente, la teoría de la probabilidad estándar señala el camino para combinar los modelos de falla de piezas individuales en un modelo general de falla de la máquina. El tiempo hasta que falla la primera de muchas partes tiene un poli-Weibull distribución. En este punto, sin embargo, el análisis puede volverse bastante complicado, y el mejor movimiento puede ser cambiar de análisis por ecuación a análisis por simulación.
Simulación de fallas de máquinas a partir de los detalles de fallas de piezas
El análisis de simulación tuvo su comienzo moderno como un derivado del Proyecto Manhattan para construir la primera bomba atómica. El método también se denomina comúnmente simulación del Monte Carlo después del centro de juego más grande del mundo en el pasado (hoy sería "simulación de Macao").
Un modelo de simulación convierte la lógica de la secuencia de eventos aleatorios en el código informático correspondiente. Luego, utiliza números (pseudo) aleatorios generados por computadora como combustible para impulsar el modelo de simulación. Por ejemplo, el tiempo de falla de cada componente se crea a partir de su distribución particular de tiempo de falla de Weibull. Luego, el más temprano de esos tiempos de falla comienza el siguiente episodio de tiempo de inactividad de la máquina.

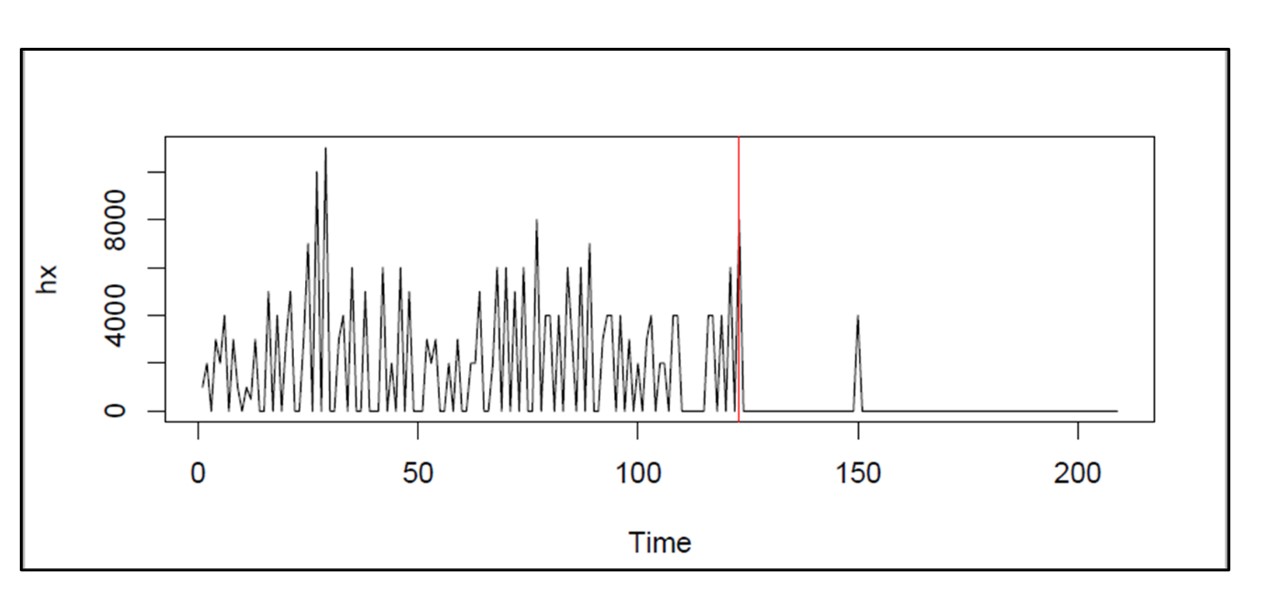
Figura 2: una simulación del tiempo de actividad de la máquina durante un año de funcionamiento
La Figura 2 muestra los resultados de una simulación del tiempo de actividad de una sola máquina. Las máquinas pasan por períodos alternos de tiempo de actividad y tiempo de inactividad. En esta simulación, se supone que el tiempo de actividad tiene una distribución exponencial con una duración promedio (MTBF = Tiempo medio antes de la falla) de 30 días. El tiempo de inactividad tiene una división de 50:50 entre 1 día si hay un repuesto disponible y 30 días si no. En la simulación que se muestra en la Figura 2, la máquina está funcionando durante 85% de los días en un año de operación.
Una fórmula aproximada para el tiempo de actividad de la máquina
Aunque la simulación de Monte Carlo puede proporcionar resultados más exactos, un modelo algebraico más simple funciona bien como aproximación y facilita ver cómo se relacionan las variables clave.
Defina las siguientes variables clave:
- MTBF = Tiempo medio antes de la falla (días)
- Pa = Probabilidad de que haya un repuesto disponible cuando se necesite
- MDTshort = Tiempo medio de inactividad si hay un repuesto disponible cuando sea necesario
- MDTlong = Tiempo medio de inactividad si no hay repuesto disponible cuando se necesita
- Uptime = Porcentaje de días en los que la máquina está en funcionamiento.
Entonces hay una aproximación simple para el tiempo de actividad:
Tiempo de actividad ≈ 100 x MTBF/(MTBF + MDTshort x Pa + MDTlong x (1-Pa)). (Ecuación 1)
La ecuación 1 nos dice que el tiempo de actividad depende de la disponibilidad de un repuesto. Si siempre hay un repuesto (Pa=1), el tiempo de actividad alcanza un valor máximo de alrededor de 100 x MTBF/(MTBF + MDTshort). Si nunca hay un repuesto disponible (Pa=0), entonces el tiempo de actividad alcanza su valor más bajo de alrededor de 100 x MTBF/(MTBF + MDTlong). Cuando el tiempo de reparación es tan largo como el tiempo típico entre fallas, el tiempo de actividad se reduce a un nivel inaceptable cerca de 50%. Si siempre hay un repuesto disponible, el tiempo de actividad puede acercarse a 100%.
Relacionar el tiempo de inactividad de la máquina con el inventario de piezas de repuesto
Minimizar el tiempo de inactividad requiere una iniciativa múltiple que implique una formación intensiva del operador, el uso de materias primas de calidad, un mantenimiento preventivo eficaz y las piezas de repuesto adecuadas. Los tres primeros establecen las condiciones para obtener buenos resultados. El último se ocupa de las contingencias.

Una vez que una máquina está inactiva, el dinero sale volando por la puerta y hay una prima en volver a ponerla en marcha pronto. Esta escena podría desarrollarse de dos maneras. El bueno tiene una pieza de repuesto lista para usar, por lo que el tiempo de inactividad se puede reducir al mínimo. El defectuoso no tiene repuestos disponibles, por lo que hay una lucha para acelerar la entrega de la pieza necesaria. En este caso, el fabricante debe asumir tanto el costo de la pérdida de producción como el costo del envío acelerado, si es que esa es una opción.
Si el sistema de inventario está diseñado correctamente, la disponibilidad de repuestos no será un impedimento importante para el tiempo de actividad de la máquina. Por el diseño de un sistema de inventario, me refiero a los resultados de varias opciones: si la política de escasez es una política de pedidos pendientes o una política de pérdida, si el ciclo de revisión del inventario es periódico o continuo, y qué puntos de pedido y cantidades de pedido se establecen.
Cuando se diseñan políticas de inventario para productos, se evalúan utilizando varios criterios. El nivel de servicio es el porcentaje de períodos de reabastecimiento que transcurren sin desabastecimiento. Tasa de llenado es el porcentaje de unidades pedidas que se suministran inmediatamente desde el stock. El nivel de inventario promedio es el número típico de unidades disponibles.
Ninguno de estos es exactamente la métrica necesaria para el almacenamiento de repuestos, aunque todos están relacionados. La métrica necesaria es Disponibilidad de artículos, que es el porcentaje de días en los que hay al menos un repuesto listo para usar. Los niveles de servicio, las tasas de llenado y los niveles de inventario más altos implican una alta disponibilidad de artículos, y hay formas de convertir de uno a otro. (Cuando se trata de varias máquinas que comparten el mismo stock de repuestos, la disponibilidad de inventario se reemplaza por la distribución de probabilidad del número de repuestos en un día determinado. Dejamos ese problema más complejo para otro día).
Claramente, mantener un buen suministro de repuestos reduce los costos del tiempo de inactividad de la máquina. Por supuesto, mantener un buen suministro de repuestos genera sus propios costos de inventario y pedidos. Este es el segundo problema de inventario del fabricante. Al igual que con cualquier decisión que involucre inventario, la clave es lograr el equilibrio adecuado entre estos dos centros de costos en competencia. Ver este artículo sobre pronóstico probabilístico para demanda intermitente para obtener orientación sobre cómo lograr ese equilibrio.