El Blog de Smart

Considere el problema de reponer el inventario. Para ser específicos, suponga que el artículo de inventario en cuestión es una pieza de repuesto. Tanto usted como su proveedor querrán saber cuánto ordenarán y cuándo. Y su sistema ERP puede estar insistiendo en que también le diga el secreto.
Modelo determinista de reabastecimiento
La forma más sencilla de obtener una respuesta decente a esta pregunta es asumir que el mundo es, bueno, simple. En este caso, simple significa "no aleatorio" o, en lenguaje geek, "determinista". En particular, pretende que el tamaño aleatorio y el tiempo de la demanda es realmente un goteo continuo de un tamaño fijo que viene en un intervalo fijo, por ejemplo, 2, 2, 2, 2, 2, 2... Si esto parece poco realista , es. La demanda real podría parecerse más a esto: 0, 1, 10, 0, 1, 0, 0, 0 con muchos ceros, picos ocasionales pero aleatorios.
Pero la sencillez tiene sus virtudes. Si pretende que la demanda promedio ocurre todos los días como un reloj, es fácil calcular cuándo deberá realizar su próximo pedido y cuántas unidades necesitará. Por ejemplo, suponga que su política de inventario es del tipo (Q,R), donde Q es una cantidad de pedido fija y R es un punto de pedido fijo. Cuando las existencias caen hasta el punto de reorden R o por debajo de este, pide Q unidades más. Para redondear la fantasía, suponga que el tiempo de reabastecimiento también es fijo: después de L días, esas Q nuevas unidades estarán en el estante listas para satisfacer la demanda.
Todo lo que necesita ahora para responder a sus preguntas es la demanda promedio por día D para el artículo. La lógica es así:
- Comienza cada ciclo de reabastecimiento con Q unidades disponibles.
- Usted agota ese stock en D unidades por día.
- Por lo tanto, alcanza el punto de pedido R después de (QR)/D días.
- Entonces, usted ordena cada (QR)/D días.
- Cada ciclo de reabastecimiento dura (QR)/D + L días, por lo que realiza un total de 365D/(Q-R+LD) pedidos por año.
- Siempre que el tiempo de entrega L < R/D, nunca se agotará y su inventario será lo más pequeño posible.
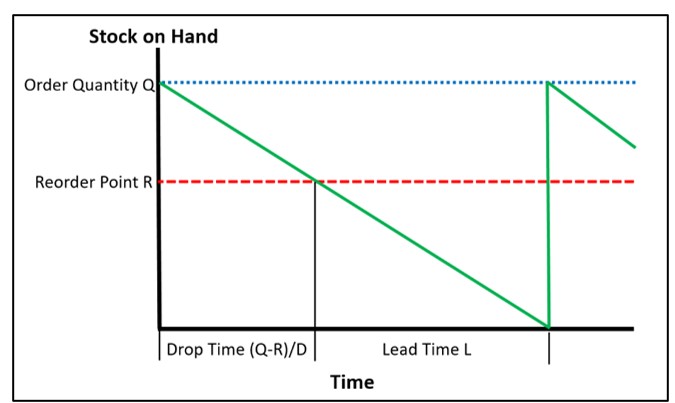
La figura 1 muestra el gráfico del inventario disponible frente al tiempo para el modelo determinista. En torno al software inteligente, nos referimos a este gráfico como el "diente de sierra determinista". El stock comienza en el nivel de la última cantidad de pedido Q. Después de disminuir constantemente durante el tiempo de caída (QR)/D, el nivel llega al punto de pedido R y activa un pedido de otras Q unidades. Durante el tiempo de entrega L, las existencias caen exactamente a cero, luego llega mágicamente el nuevo pedido y comienza el siguiente ciclo.
Este modelo tiene dos cosas a su favor. No requiere más que álgebra de secundaria y combina (casi) todos los factores relevantes para responder las dos preguntas relacionadas: ¿Cuándo tendremos que hacer el próximo pedido? ¿Cuántos pedidos haremos en un año?
Modelo Probabilístico de Reposición
No es sorprendente que si eliminamos parte de la fantasía del modelo determinista, obtengamos información más útil. El modelo probabilístico incorpora toda la desordenada aleatoriedad del problema del mundo real: la incertidumbre tanto en el momento como en el tamaño de la demanda, la variación en el tiempo de reabastecimiento y las consecuencias de esos dos factores: la posibilidad de que las existencias disponibles no alcancen el reabastecimiento. punto, la probabilidad de que haya un desabastecimiento, la variabilidad en el tiempo hasta el próximo pedido y el número variable de pedidos ejecutados en un año.
El modelo probabilístico funciona simulando las consecuencias de una demanda incierta y un tiempo de entrega variable. Mediante el análisis de los patrones históricos de demanda del artículo (y la exclusión de cualquier observación registrada durante un período en el que la demanda pudo haber sido fundamentalmente diferente), los métodos estadísticos avanzados crean una cantidad ilimitada de escenarios de demanda realistas. Se aplica un análisis similar a los registros de los plazos de entrega de los proveedores. La combinación de estos escenarios de oferta y demanda con las reglas operativas de cualquier política de control de inventario produce escenarios de la cantidad de piezas disponibles. De estos escenarios, podemos extraer resúmenes de los diferentes intervalos entre órdenes.
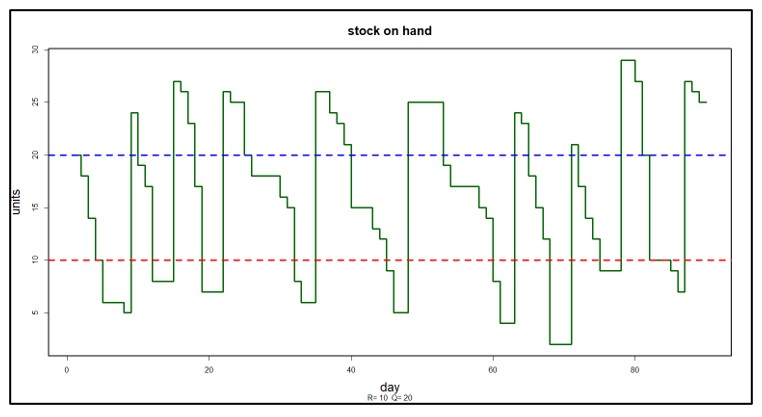
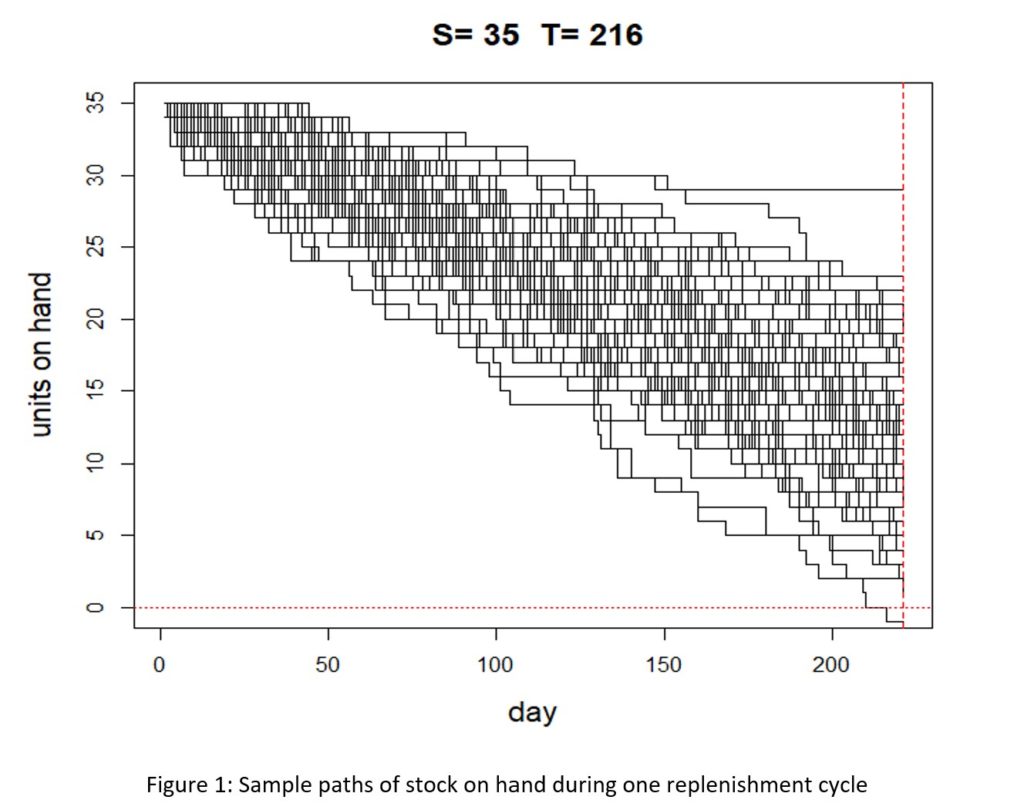
La Figura 2 muestra un ejemplo de un escenario probabilístico; la demanda es aleatoria y el artículo se administra utilizando el punto de pedido R = 10 y la cantidad de pedido Q = 20. Atrás quedó el diente de sierra determinista; en su lugar hay algo más complejo y realista (la Escalera Probabilística). Durante los 90 días simulados de operación, se realizaron 9 pedidos y el tiempo entre pedidos varió claramente.
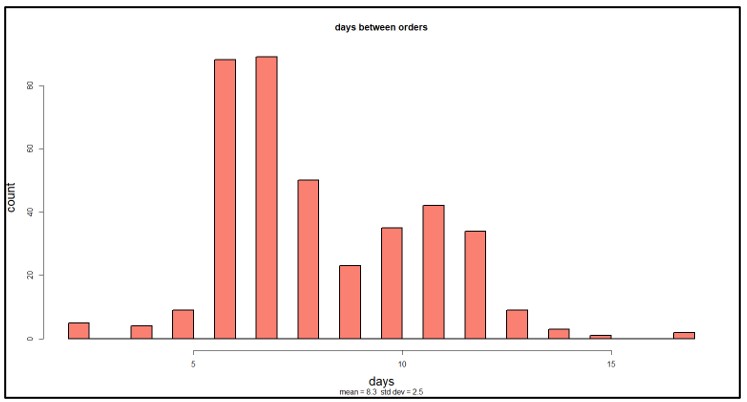
Usando el modelo probabilístico, las respuestas a las dos preguntas (cuánto tiempo entre pedidos y cuántos en un año) se expresan como distribuciones de probabilidad que reflejan las probabilidades relativas de varios escenarios. La figura 3 muestra la distribución del número de días entre pedidos después de diez años de funcionamiento simulado. Si bien el promedio es de aproximadamente 8 días, el número real varía ampliamente, de 2 a 17.
En lugar de decirle a su proveedor que realizará X pedidos el próximo año, ahora puede proyectar X ± Y pedidos, y su proveedor conoce mejor sus riesgos al alza y a la baja. Mejor aún, podría proporcionar la distribución completa como la respuesta más rica posible.
Subiendo la escalera aleatoria hacia una mayor eficiencia
Ir más allá del modelo determinista de inventario abre nuevas posibilidades para optimizar las operaciones. En primer lugar, el modelo probabilístico permite una evaluación realista del riesgo de desabastecimiento. El modelo simple en la Figura 1 implica que nunca hay un desabastecimiento, mientras que los escenarios probabilísticos permiten la posibilidad (aunque en la Figura 2 solo hubo una llamada cercana alrededor del día 70). Una vez que se conoce el riesgo, el software puede optimizar buscando en el "espacio de diseño" (es decir, todos los valores posibles de R y Q) para encontrar un diseño que cumpla con un nivel objetivo de riesgo de desabastecimiento a un costo mínimo. El valor del modelo determinista en este análisis más realista es que proporciona un buen punto de partida para la búsqueda a través del espacio de diseño.
Resumen
El software moderno proporciona respuestas a preguntas operativas con varios grados de detalle. Utilizando el ejemplo del tiempo entre pedidos de reabastecimiento, hemos demostrado que la respuesta se puede calcular de manera aproximada pero rápida mediante un modelo determinista simple. Pero también se puede proporcionar con mucho más detalle con toda la variabilidad expuesta por un modelo probabilístico. Pensamos en estas alternativas como complementarias. El modelo determinista agrupa todas las variables clave en un formato fácil de entender. El modelo probabilístico proporciona el realismo adicional que los profesionales esperan y respalda la búsqueda efectiva de opciones óptimas de punto de pedido y cantidad de pedido.
Escenarios de demanda diaria
En este Videoblog explicaremos cómo la previsión de series temporales se ha convertido en una herramienta fundamental, especialmente a nivel diario, en la que Smart Software ha sido pionero desde sus inicios hace más de cuarenta años. La evolución de las prácticas comerciales de incrementos temporales anuales a incrementos temporales más refinados, como el análisis de datos mensual y ahora diario, ilustra un cambio significativo en las estrategias operativas.

Operaciones irregulares
Este blog trata sobre "operaciones irregulares". Smart Software está en el proceso de adaptar nuestros productos para ayudarle a afrontar sus propias operaciones irregulares. Esto es una vista previa.

Encontrar su lugar en la curva de compensación del inventario
Este videoblog contiene información esencial para quienes trabajan con las complejidades de la gestión de inventario. La sesión se centra en lograr el equilibrio adecuado dentro de la curva de compensación de acciones, invitando a los espectadores a comprender la importancia profundamente arraigada de este equilibrio.