Algunas empresas invierten en software que les ayude a gestionar su inventario, ya sean repuestos o productos terminados. Pero un número sorprendente de personas juegan el juego de adivinar el inventario todos los días, confiando en un “tripa dorada” imaginario o en la simple suerte para establecer sus parámetros de control de inventario. Pero, ¿qué tipo de resultados espera con ese enfoque?
¿Qué tan bueno eres para intuir los valores correctos? Esta publicación de blog lo desafía a adivinar los mejores valores mínimos y máximos para un artículo de inventario hipotético. Le mostraremos su historial de demanda, le brindaremos algunos datos relevantes, luego podrá elegir los valores mínimos y máximos y ver qué tan bien funcionarían. ¿Listo?
El reto
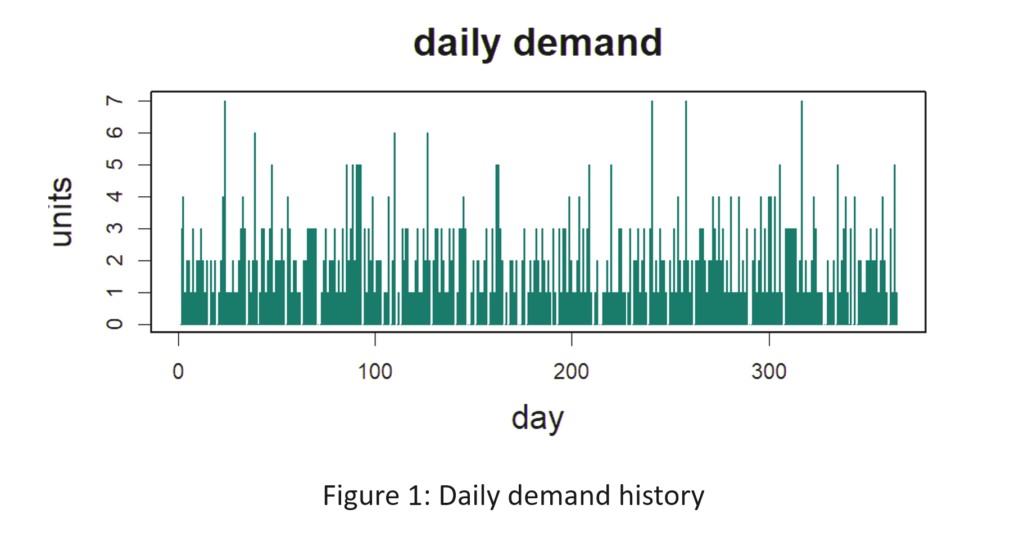
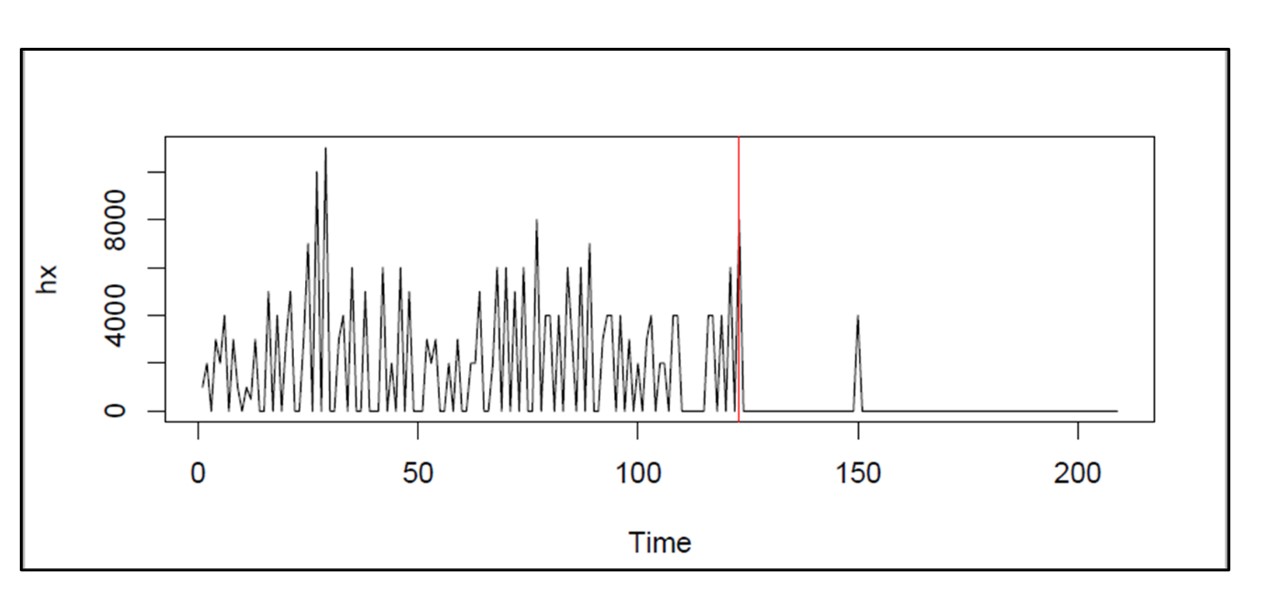
La Figura 1 muestra el historial de demanda diaria del artículo. La demanda promedio es de 2 unidades por día. El plazo de reposición es de 10 días constantes (lo cual no es realista pero juega a su favor). Los pedidos que no se pueden completar inmediatamente desde el stock no se pueden retrasar y se pierden. Desea lograr al menos una tasa de cumplimiento de 80%, pero no a cualquier costo. También desea minimizar la cantidad promedio de unidades disponibles y al mismo tiempo lograr al menos una tasa de llenado de 80%. ¿Qué valores mínimos y máximos producirían una tasa de llenado del 80% con el número promedio más bajo de unidades disponibles? [Grabe sus respuestas para comprobarlas más tarde. La solución aparece a continuación, al final del artículo.]
Calcular los mejores valores mínimos y máximos
La forma de determinar los mejores valores es utilizar un gemelo digital, también conocido como simulación de Monte Carlo. El análisis crea una multitud de escenarios de demanda y los pasa a través de la lógica matemática del sistema de control de inventario para ver qué valores tomarán los indicadores clave de desempeño (KPI).
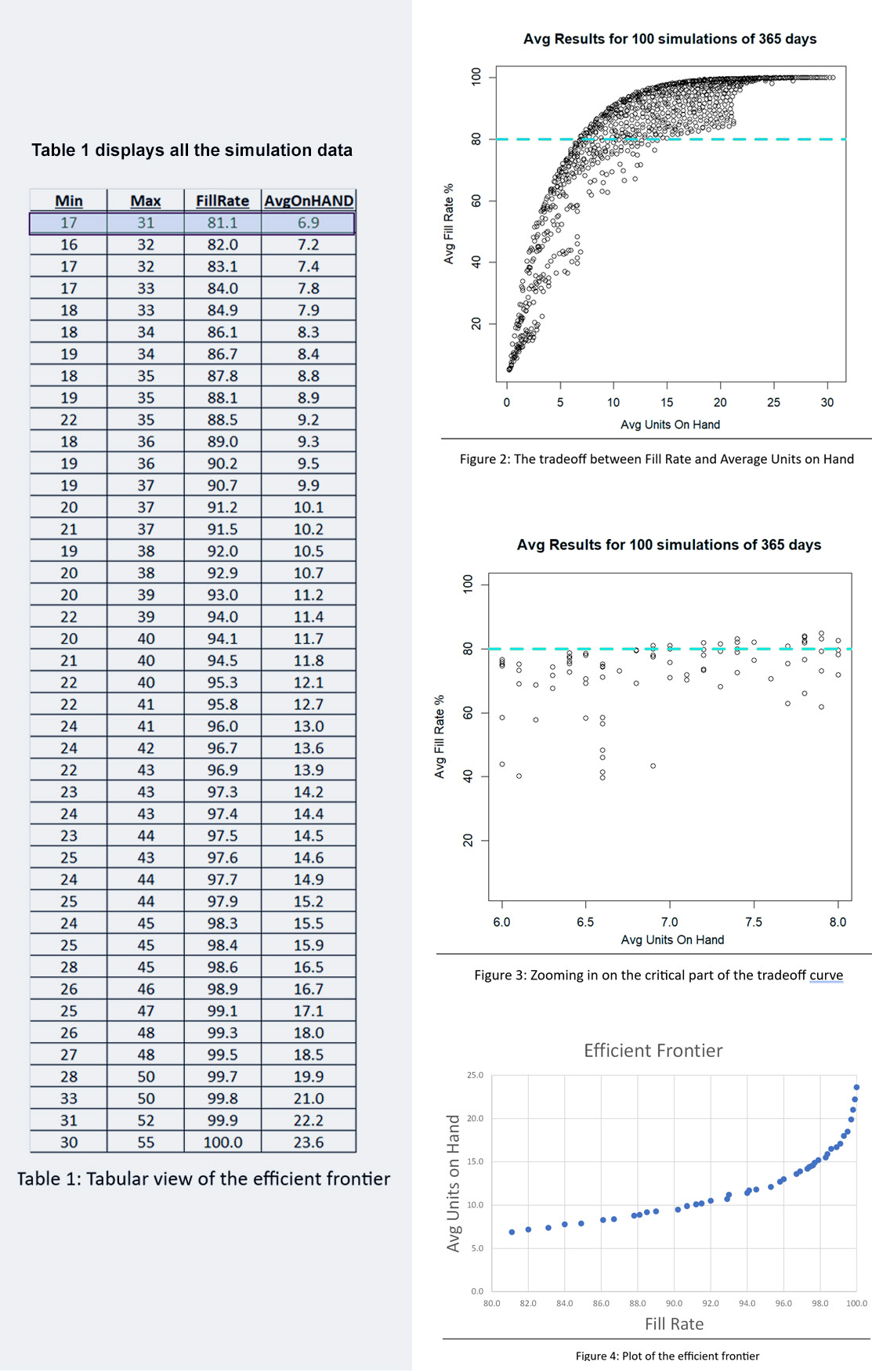
Construimos un gemelo digital para este problema y lo ejercitamos sistemáticamente con 1085 pares de valores mínimos y máximos. Para cada par, simulamos 365 días de funcionamiento un total de 100 veces. Luego promediamos los resultados para evaluar el desempeño del par Mínimo/Máximo en términos de dos KPI: tasa de cumplimiento e inventario disponible promedio.
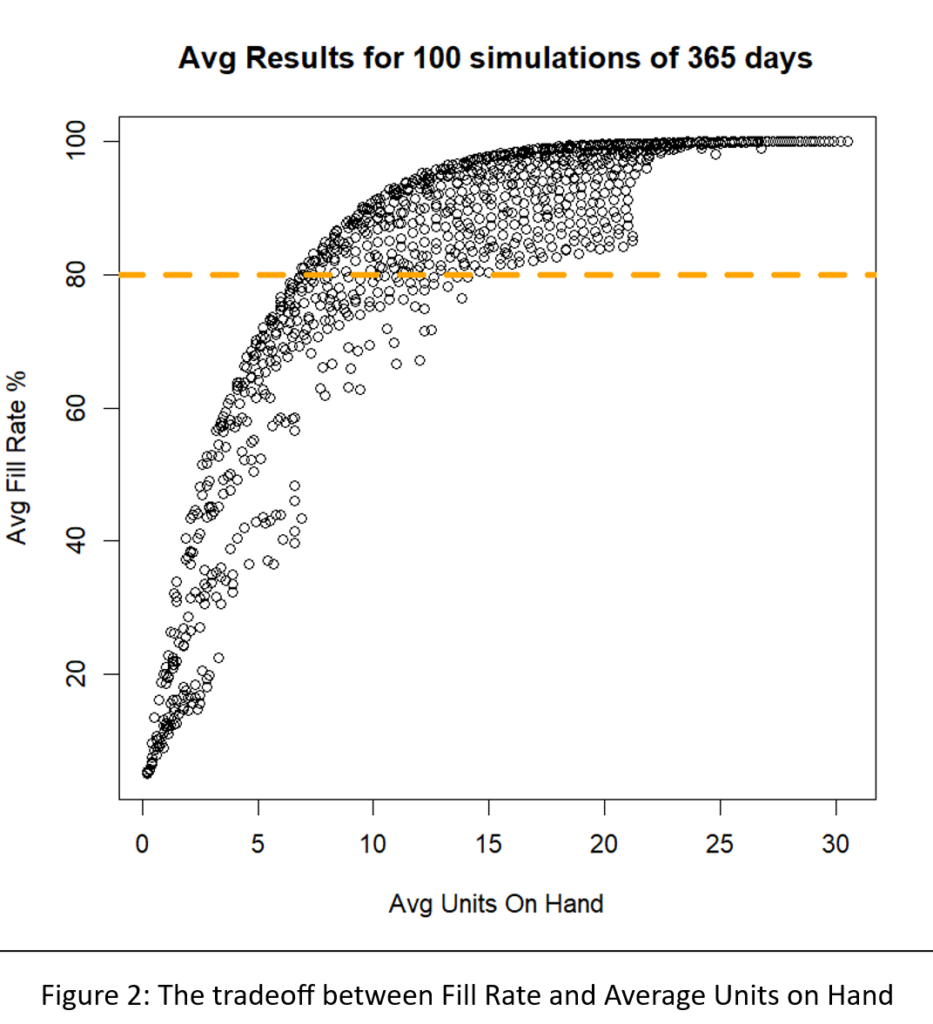
La Figura 2 muestra los resultados. La compensación inherente entre el tamaño del inventario y la tasa de cumplimiento es clara en la figura: si desea una tasa de cumplimiento más alta, debe aceptar un inventario más grande. Sin embargo, en cada nivel de inventario hay un rango de tasas de llenado, por lo que el juego consiste en encontrar el par mínimo/máximo que produzca la tasa de llenado más alta para cualquier tamaño de inventario determinado.
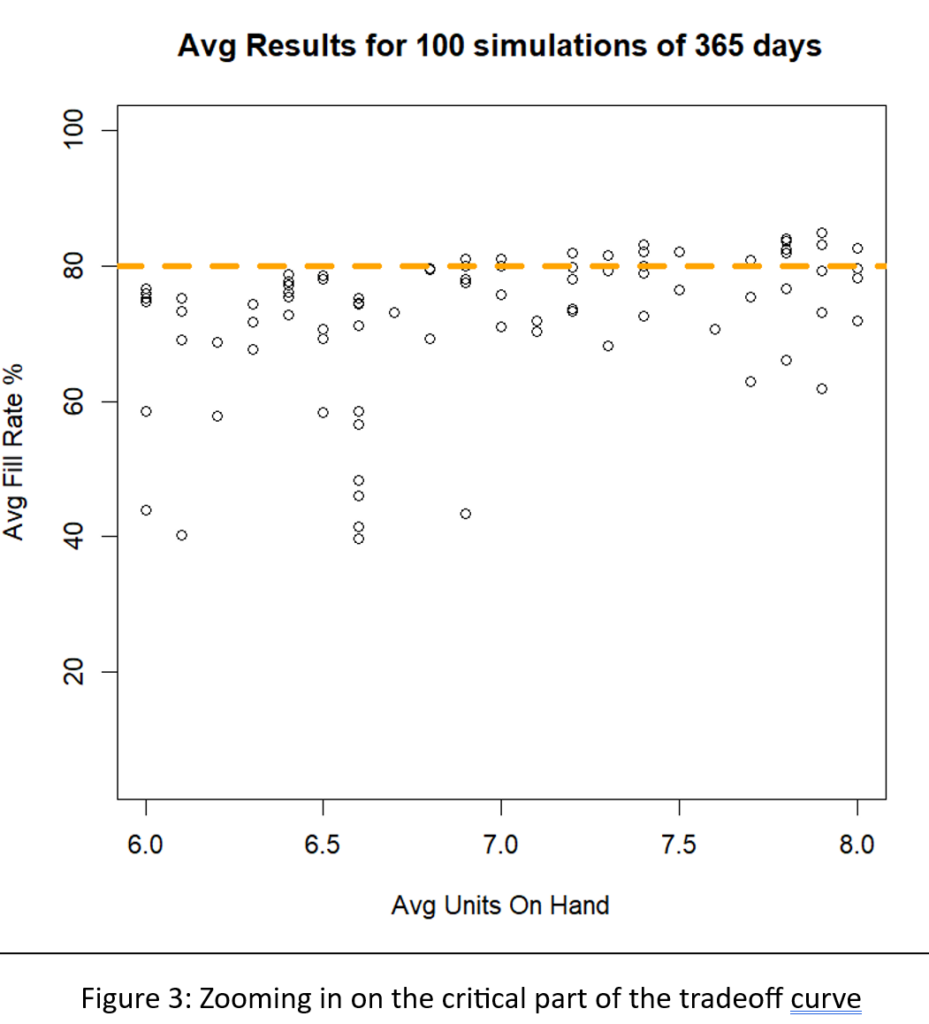
Una forma diferente de interpretar la Figura 2 es centrarse en la línea verde discontinua que marca la tasa de llenado objetivo del 80%. Hay muchos pares Min/Max que pueden alcanzar cerca del objetivo 80%, pero difieren en el tamaño del inventario de aproximadamente 6 a aproximadamente 8 unidades. La Figura 3 amplía esa región de la Figura 2 para mostrar una gran cantidad de pares Mín/Máx que son competitivos.
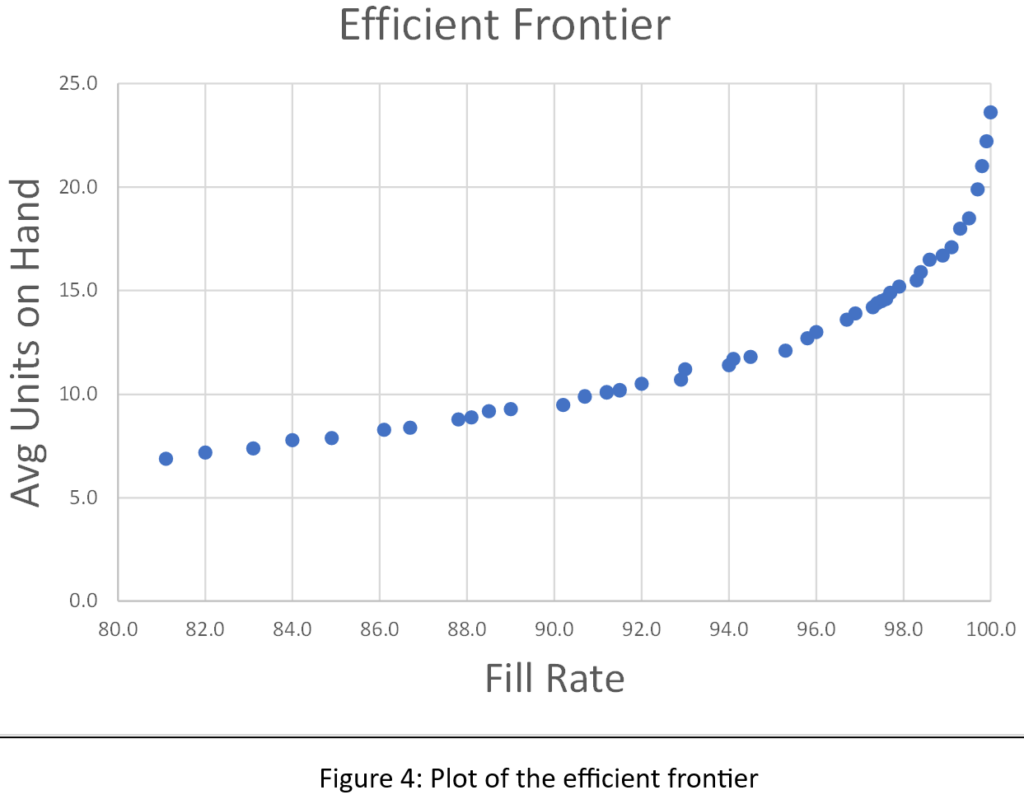
Clasificamos los resultados de las 1.085 simulaciones para identificar lo que los economistas llaman la frontera eficiente. La frontera eficiente es el conjunto de pares mínimo/máximo más eficientes para explotar el equilibrio entre la tasa de llenado y las unidades disponibles. Es decir, es una lista de pares mínimo/máximo que proporciona la forma más económica de lograr cualquier tasa de llenado deseada, no solo 80%. La Figura 4 muestra la frontera eficiente para este problema. Moviéndose de izquierda a derecha, puede leer el precio más bajo que tendría que pagar (medido por el tamaño promedio del inventario) para lograr cualquier tasa de cumplimiento objetivo. Por ejemplo, para lograr una tasa de llenado del 90%, tendría que tener un inventario promedio de aproximadamente 10 unidades.
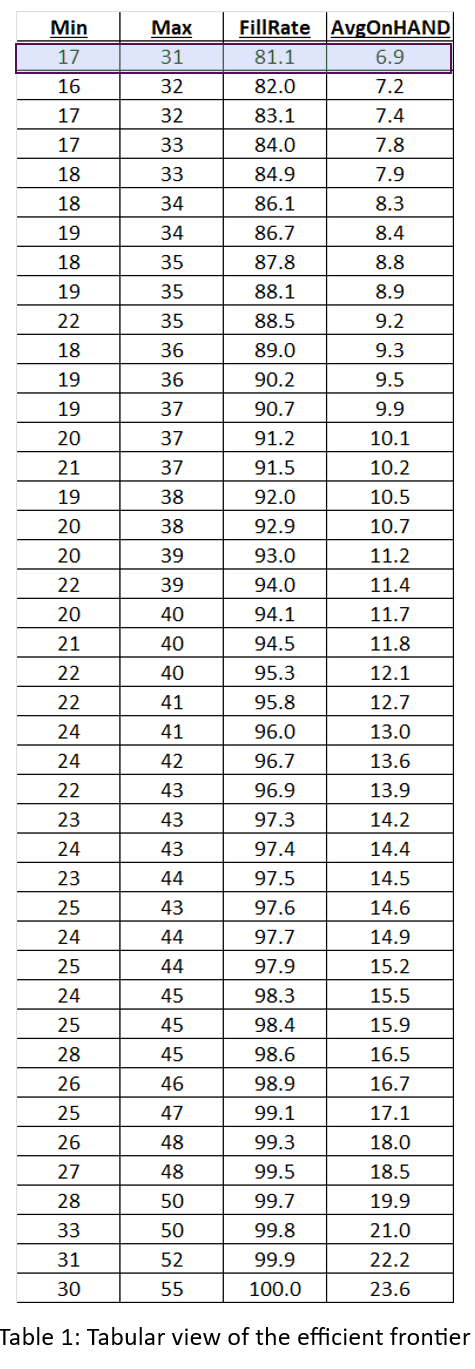
Las figuras 2, 3 y 4 muestran resultados para varios pares Mín/Máx, pero no muestran los valores de Mín y Máx detrás de cada punto. La Tabla 1 muestra todos los datos de la simulación: los valores mínimo, máximo, unidades promedio disponibles y tasa de llenado. La respuesta al juego de adivinanzas está resaltada en la primera línea de la tabla: Mín=7 y Máx=131. ¿Obtuviste la respuesta correcta o algo parecido?2? ¿Quizás llegaste a la frontera eficiente?
Conclusiones
Tal vez tuviste suerte, o tal vez tengas un intestino dorado, pero es más probable que no hayas obtenido la respuesta correcta, y es aún más probable que ni siquiera lo hayas intentado. Encontrar la respuesta correcta es extremadamente difícil sin utilizar el gemelo digital. Adivinar no es profesional.
Un paso adelante de las conjeturas es “adivinar y ver”, en el que implementas tu conjetura y luego esperas un tiempo (¿meses?) para ver si te gustan los resultados. Esa táctica es al menos “científica”, pero es ineficiente.
Ahora considere el esfuerzo de encontrar los mejores pares (Min, Max) para miles de artículos. A esa escala, hay aún menos justificación para jugar el Juego de Adivinar el Inventario. La respuesta correcta es jugarlo... Inteligente3.
1 Esta respuesta tiene una ventaja, ya que logra una tasa de llenado un poco mayor que 80% con un tamaño de inventario promedio más bajo que la combinación Mín./Máx. que alcanzó exactamente 80%. En otras palabras, (7,13) está en la frontera eficiente.
2 Debido a que estos resultados provienen de una simulación en lugar de una ecuación matemática exacta, existe un cierto margen de error asociado con cada tasa de llenado y nivel de inventario estimados. Sin embargo, debido a que los resultados promedio se basaron en 100 simulaciones cada 365 días, los márgenes de error son pequeños. En todos los experimentos, los errores estándar promedio en la tasa de llenado y el inventario medio fueron, respectivamente, sólo 0,009% y 0,129 unidades.
3 En caso de que no lo sepas, uno de los fundadores de Smart Software fue... Charlie Smart.