Deze blog geeft een overzicht van dit onderwerp, geschreven voor niet-experts. Het
- legt uit waarom je deze blog zou willen lezen.
- somt de verschillende soorten "machine-onderhoud" op.
- legt uit wat 'probabilistische modellering' is.
- beschrijft modellen voor het voorspellen van uitvaltijd.
- legt uit wat deze modellen voor u kunnen betekenen.
Belang van uitvaltijd
Als je dingen voor de verkoop maakt, heb je machines nodig om die dingen te maken. Als uw machines in bedrijf zijn, heeft u een goede kans om geld te verdienen. Als uw machines niet werken, verliest u kansen om geld te verdienen. Omdat downtime zo fundamenteel is, is het de moeite waard om geld te investeren en de downtime te minimaliseren. Met denken bedoel ik kansberekening, aangezien stilstandtijd van de machine is inherent een willekeurig fenomeen. Waarschijnlijkheidsmodellen kan het onderhoudsbeleid sturen.
Beleid voor machineonderhoud
Onderhoud is uw verdediging tegen uitvaltijd. Er zijn meerdere soorten onderhoudsbeleid, variërend van "Niets doen en wachten op falen" tot geavanceerde analytische benaderingen met sensoren en faalkansmodellen.
Een handige lijst met onderhoudsbeleid is:
- Achterover leunen en wachten op problemen, en dan nog wat rondhangen en afvragen wat te doen als er onvermijdelijk problemen optreden. Dit is zo dwaas als het klinkt.
- Hetzelfde als hierboven, behalve dat u zich voorbereidt op het falen om de uitvaltijd te minimaliseren, bijvoorbeeld door reserveonderdelen op te slaan.
- Periodiek controleren op dreigende problemen in combinatie met interventies zoals het smeren van bewegende onderdelen of het vervangen van versleten onderdelen.
- De timing van onderhoud baseren op gegevens over de machineconditie in plaats van te vertrouwen op een vast schema; vereist voortdurende gegevensverzameling en -analyse. Dit wordt conditiegestuurd onderhoud genoemd.
- Gegevens over de machineconditie agressiever gebruiken door deze om te zetten in voorspellingen van uitvaltijd en suggesties voor te nemen stappen om uitval te vertragen. Dit wordt voorspellend onderhoud genoemd.
De laatste drie soorten onderhoud zijn afhankelijk van kansberekening om een onderhoudsschema op te stellen, of om te bepalen wanneer gegevens over de machineconditie moeten worden ingegrepen, of om te berekenen wanneer een storing kan optreden en hoe deze het beste kan worden uitgesteld.
Waarschijnlijkheidsmodellen van machinestoring
Hoe lang een machine zal draaien voordat deze uitvalt, is een willekeurige variabele. Zo is de tijd die het zal besteden naar beneden. Kansrekening is het deel van de wiskunde dat zich bezighoudt met willekeurige variabelen. Willekeurige variabelen worden beschreven door hun kansverdelingen, bijvoorbeeld, wat is de kans dat de machine 100 uur zal draaien voordat hij uitvalt? 200 uur? Of wat is de kans dat de machine na 100 uur of 200 uur nog steeds werkt?
Een subveld genaamd "betrouwbaarheidstheorie" beantwoordt dit soort vragen en behandelt verwante concepten zoals Mean Time Before Failure (MTBF), wat een verkorte samenvatting is van de informatie die is gecodeerd in de kansverdeling van tijd vóór mislukking.
Figuur 1 toont gegevens over de tijd vóór uitval van airconditioningunits. Dit type plot geeft de cumulatieve kansverdeling en toont de kans dat een eenheid na enige tijd is uitgevallen. Figuur 2 toont a betrouwbaarheidsfunctie:, het plotten van hetzelfde type informatie in een omgekeerd formaat, dat wil zeggen, het weergeven van de kans dat een eenheid na verloop van tijd nog steeds functioneert.
In figuur 1 geven de blauwe vinkjes naast de x-as de tijdstippen weer waarop individuele airconditioners faalden; dit zijn de basisgegevens. De zwarte curve toont het cumulatieve aandeel van eenheden die in de loop van de tijd zijn mislukt. De rode curve is een wiskundige benadering van de zwarte curve – in dit geval een exponentiële verdeling. De grafieken laten zien dat ongeveer 80 procent van de units zal uitvallen voordat ze 100 uur in bedrijf zijn.
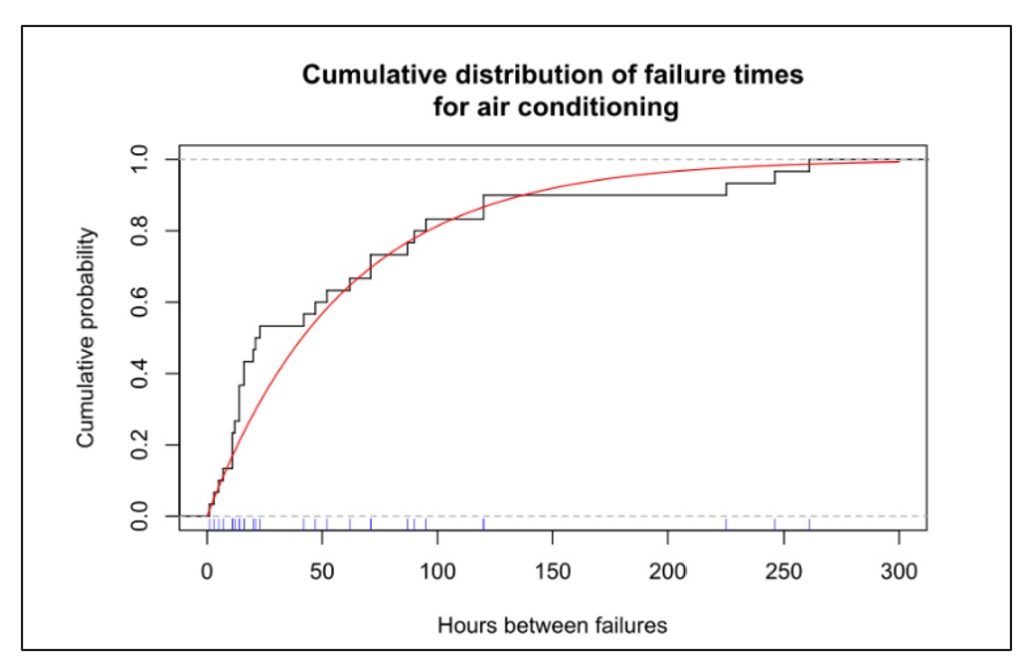
Figuur 1 Cumulatieve distributiefunctie van uptime voor airconditioners
Waarschijnlijkheidsmodellen kunnen worden toegepast op een afzonderlijk onderdeel of component of subsysteem, op een verzameling gerelateerde onderdelen (bijv. "het hydraulische systeem") of op een volledige machine. Elk van deze kan worden beschreven door de kansverdeling van de tijd voordat ze falen.
Figuur 2 toont de betrouwbaarheidsfunctie van zes subsystemen in een machine voor het graven van tunnels. De plot laat zien dat het meest betrouwbare subsysteem de snijarmen zijn en het minst betrouwbare het watersubsysteem. De betrouwbaarheid van het hele systeem kan worden benaderd door alle zes curven te vermenigvuldigen (omdat het systeem als geheel werkt, moet elk subsysteem functioneren), wat zou resulteren in een zeer korte interval voordat er iets misgaat.
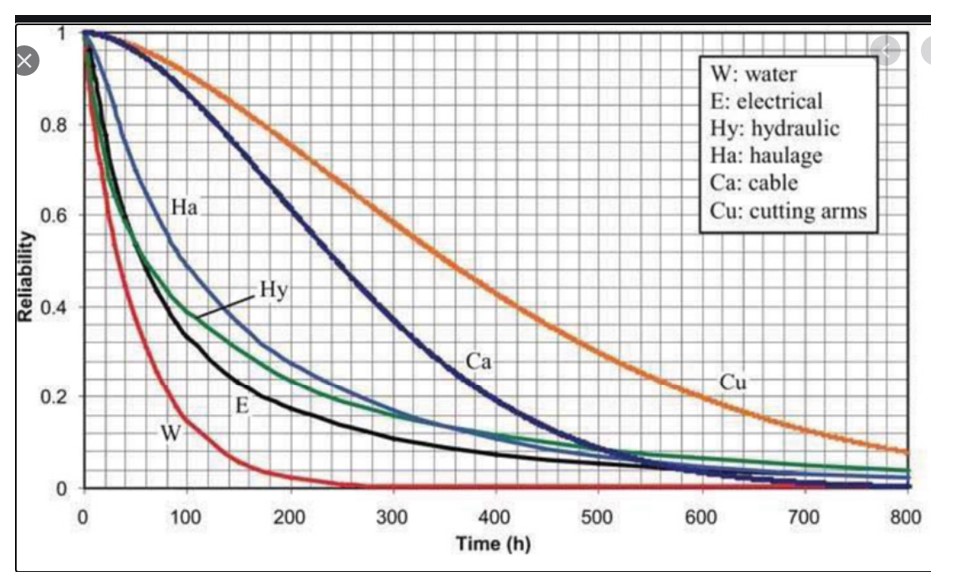
Figuur 2 Voorbeelden van kansverdelingen van subsystemen in een tunnelmachine
Verschillende factoren zijn van invloed op de verdeling van de tijd voor falen. Investeren in betere onderdelen verlengt de levensduur van het systeem. Investeren in redundantie ook. Dat geldt ook voor het vervangen van gebruikte paren door nieuwe.
Zodra een kansverdeling beschikbaar is, kan deze worden gebruikt om een willekeurig aantal wat-als-vragen te beantwoorden, zoals hieronder wordt geïllustreerd in het gedeelte over de voordelen van modellen.
Benaderingen voor het modelleren van machinebetrouwbaarheid
Waarschijnlijkheidsmodellen kunnen ofwel de meest elementaire eenheden beschrijven, zoals individuele systeemcomponenten (Figuur 2), of verzamelingen van basiseenheden, zoals volledige machines (Figuur 1). In feite kan een hele machine worden gemodelleerd als een enkele eenheid of als een verzameling componenten. Als een hele machine als een enkele eenheid wordt behandeld, vertegenwoordigt de kansverdeling van de levensduur een samenvatting van het gecombineerde effect van de levensduurverdelingen van elk onderdeel.
Als we een model van een hele machine hebben, kunnen we naar modellen van verzamelingen machines springen. Als we in plaats daarvan beginnen met modellen van de levensduur van individuele componenten, dan moeten we die individuele modellen op de een of andere manier combineren tot een algemeen model van de hele machine.
Dit is waar de wiskunde harig kan worden. Modellering vereist altijd een verstandig evenwicht tussen vereenvoudiging, zodat sommige resultaten mogelijk zijn, en complicaties, zodat alle resultaten die naar voren komen realistisch zijn. De gebruikelijke truc is om aan te nemen dat storingen van de afzonderlijke onderdelen van het systeem onafhankelijk van elkaar optreden.
Als we ervan uit kunnen gaan dat storingen onafhankelijk optreden, is het meestal mogelijk om verzamelingen van machines te modelleren. Stel bijvoorbeeld dat een productielijn vier machines heeft die hetzelfde product produceren. Met een betrouwbaarheidsmodel voor één machine (zoals in figuur 1) kunnen we bijvoorbeeld voorspellen hoe groot de kans is dat over een week nog maar drie van de machines werken. Ook hier kan zich een complicatie voordoen: de kans dat een machine die vandaag werkt, morgen nog werkt, hangt vaak af van hoe lang het geleden is sinds de laatste storing. Als de tijd tussen storingen een exponentiële verdeling heeft zoals in figuur 1, dan blijkt dat het tijdstip van de volgende storing niet afhangt van hoe lang het geleden is sinds de laatste storing. Helaas hebben veel of zelfs de meeste systemen geen exponentiële distributies van uptime, dus de complicatie blijft.
Erger nog, als we beginnen met modellen van veel individuele componentbetrouwbaarheid, kan het bijna onmogelijk zijn om ons op te werken tot het voorspellen van uitvaltijden voor de hele complexe machine als we rechtstreeks met alle relevante vergelijkingen proberen te werken. In dergelijke gevallen is de enige praktische manier om resultaten te krijgen het gebruik van een andere stijl van modelleren: Monte Carlo-simulatie.
Monte Carlo-simulatie is een manier om berekening te vervangen door analyse wanneer het mogelijk is om willekeurige scenario's van systeemwerking te creëren. Het gebruik van simulatie om machinebetrouwbaarheid te extrapoleren uit de betrouwbaarheid van componenten werkt als volgt.
- Begin met de cumulatieve distributiefuncties (Figuur 1) of betrouwbaarheidsfuncties (Figuur 2) van elk machineonderdeel.
- Maak een willekeurig voorbeeld van de levensduur van elke component om een set voorbeeldfouten te krijgen die consistent zijn met de betrouwbaarheidsfunctie.
- Gebruik de logica van hoe componenten aan elkaar gerelateerd zijn, bereken de uitvaltijd van de hele machine.
- Herhaal stap 1-3 vele malen om het volledige scala aan mogelijke levensduur van de machine te zien.
- U kunt desgewenst het gemiddelde van de resultaten van stap 4 nemen om de levensduur van de machine samen te vatten met metrische gegevens zoals de MTBF of de kans dat de machine meer dan 500 uur zal draaien voordat deze defect raakt.
Stap 1 zou een beetje ingewikkeld zijn als we geen mooi kansmodel hebben voor de levensduur van een component, bijvoorbeeld zoiets als de rode lijn in figuur 1.
Stap 2 kan een zorgvuldige boekhouding vereisen. Naarmate de tijd verstrijkt in de simulatie, zullen sommige componenten defect raken en worden vervangen, terwijl andere door blijven gaan. Tenzij de levensduur van een component een exponentiële verdeling heeft, zal de resterende levensduur afhangen van hoe lang de component continu in gebruik is geweest. Dus deze stap moet rekening houden met de verschijnselen van branden in of verslijten.
Stap 3 verschilt van de andere doordat er wat achtergrondwiskunde voor nodig is, zij het van een eenvoudig type. Als Machine A alleen werkt als beide componenten 1 en 2 werken, dan (ervan uitgaande dat een storing van de ene component geen invloed heeft op de storing van de andere)
Kans [A werkt] = Kans [1 werkt] x Kans [2 werkt].
Als in plaats daarvan Machine A werkt als component 1 werkt of component 2 werkt of beide werken, dan
Waarschijnlijkheid [A faalt] = Waarschijnlijkheid [1 faalt] x Waarschijnlijkheid [2 faalt]
dus Waarschijnlijkheid [A werkt] = 1 – Waarschijnlijkheid [A faalt].
Stap 4 kan het creëren van duizenden scenario's omvatten om het volledige scala aan willekeurige uitkomsten te tonen. Berekenen is snel en goedkoop.
Stap 5 kan variëren, afhankelijk van de doelen van de gebruiker. Het berekenen van de MTBF is standaard. Kies andere die bij het probleem passen. Naast de samenvattende statistieken die in stap 5 worden geleverd, kunnen individuele simulatieruns worden uitgezet om intuïtie op te bouwen over de willekeurige dynamiek van machine-uptime en downtime. Afbeelding 3 toont een voorbeeld van een enkele machine met afwisselende cycli van uptime en downtime, resulterend in 85% uptime.
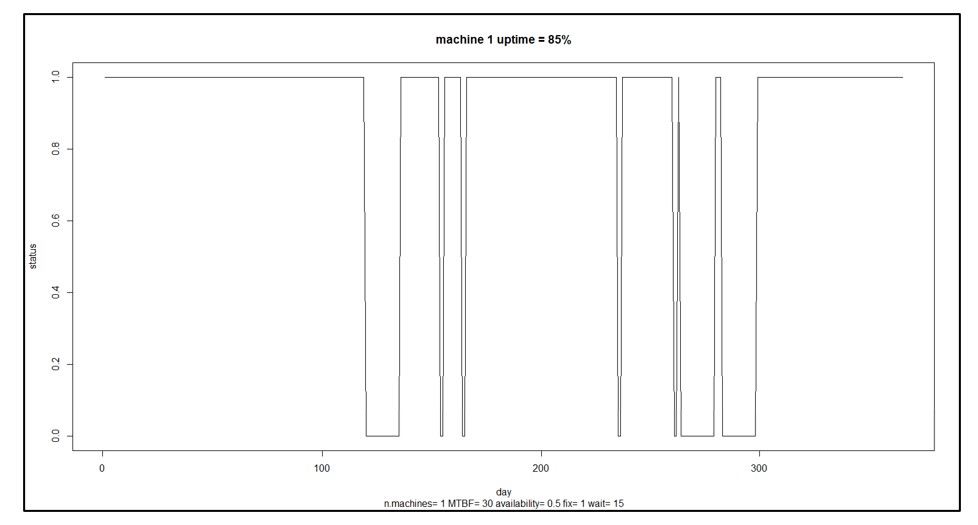
Afbeelding 3 Een voorbeeldscenario voor een enkele machine
Voordelen van machinebetrouwbaarheidsmodellen
In afbeelding 3 is de machine 85% van de tijd in gebruik. Dat is misschien niet goed genoeg. U heeft misschien ideeën over hoe u de betrouwbaarheid van de machine kunt verbeteren. U kunt bijvoorbeeld de betrouwbaarheid van component 3 verbeteren door een nieuwere, betere versie van een andere leverancier te kopen. Hoeveel zou dat helpen? Dat is moeilijk te raden: component 3 is misschien maar een van de vele en misschien niet de zwakste schakel, en hoeveel de verandering loont, hangt af van hoeveel beter de nieuwe zou zijn. Misschien moet je een specificatie voor component 3 ontwikkelen die je vervolgens kunt kopen bij potentiële leveranciers, maar hoe lang moet component 3 meegaan om een materiële impact te hebben op de MTBF van de machine?
Dit is waar het hebben van een model loont. Zonder model vertrouw je op giswerk. Met een model kunt u speculaties over wat-als-situaties omzetten in nauwkeurige schattingen. U kunt bijvoorbeeld analyseren hoe een toename van 10% in MTBF voor component 3 zich zou vertalen in een verbetering van MTBF voor de hele machine.
Een ander voorbeeld: stel dat u zeven machines heeft die een belangrijk product produceren. U berekent dat u zes van de zeven moet inzetten om een grote order van uw ene grote klant te vervullen, zodat er één machine overblijft om de vraag van een aantal diverse kleine klanten af te handelen en als reserve te dienen. Een betrouwbaarheidsmodel voor elke machine zou kunnen worden gebruikt om de waarschijnlijkheid van verschillende onvoorziene omstandigheden in te schatten: alle zeven machines werken en de levensduur is goed; zes machines werken, zodat u in ieder geval uw belangrijkste klant tevreden kunt houden; slechts vijf machines werken, dus u moet iets onderhandelen met uw belangrijkste klant, enz.
Samengevat kunnen waarschijnlijkheidsmodellen van machine- of componentstoringen de basis vormen voor het omzetten van faaltijdgegevens in slimme zakelijke beslissingen.
Lees meer over Maximaliseer machine-uptime met probabilistische modellering
Lees meer over Probabilistische prognoses voor intermitterende vraag