Probabilistische scenario's zijn reeksen gegevenspunten die worden gegenereerd om potentiële situaties uit de echte wereld weer te geven. In tegenstelling tot scenario's in oorlogsspellen of andere simulaties zijn dit synthetische tijdreeksen die worden gebruikt als input voor systeemmodellen of als intuïtiebouwers voor besluitvormers.
Scenario's van de toekomstige vraag naar artikelen kunnen bijvoorbeeld worden ingevoerd in Monte Carlo-simulatiemodellen van voorraadbeheersystemen, waardoor een virtueel laboratorium ontstaat waarin de gevolgen van managementbeslissingen kunnen worden onderzocht, zoals het wijzigen van bestelpunten en/of bestelhoeveelheden. Bovendien kunnen grafieken van meetgegevens, zoals voorhanden voorraad of stockouts, voorraadplanners helpen hun ‘gevoel’ voor de willekeur die inherent is aan hun activiteiten te verdiepen.
Figuur 1 toont dagelijkse vraagscenario's die zijn gegenereerd op basis van een enkele waargenomen vraagreeks die gedurende één jaar is geregistreerd. Merk op dat hetzelfde proces voor het genereren van gegevens er in detail “heel anders uit kan zien” van monster tot monster. Dit bootst het echte leven na.
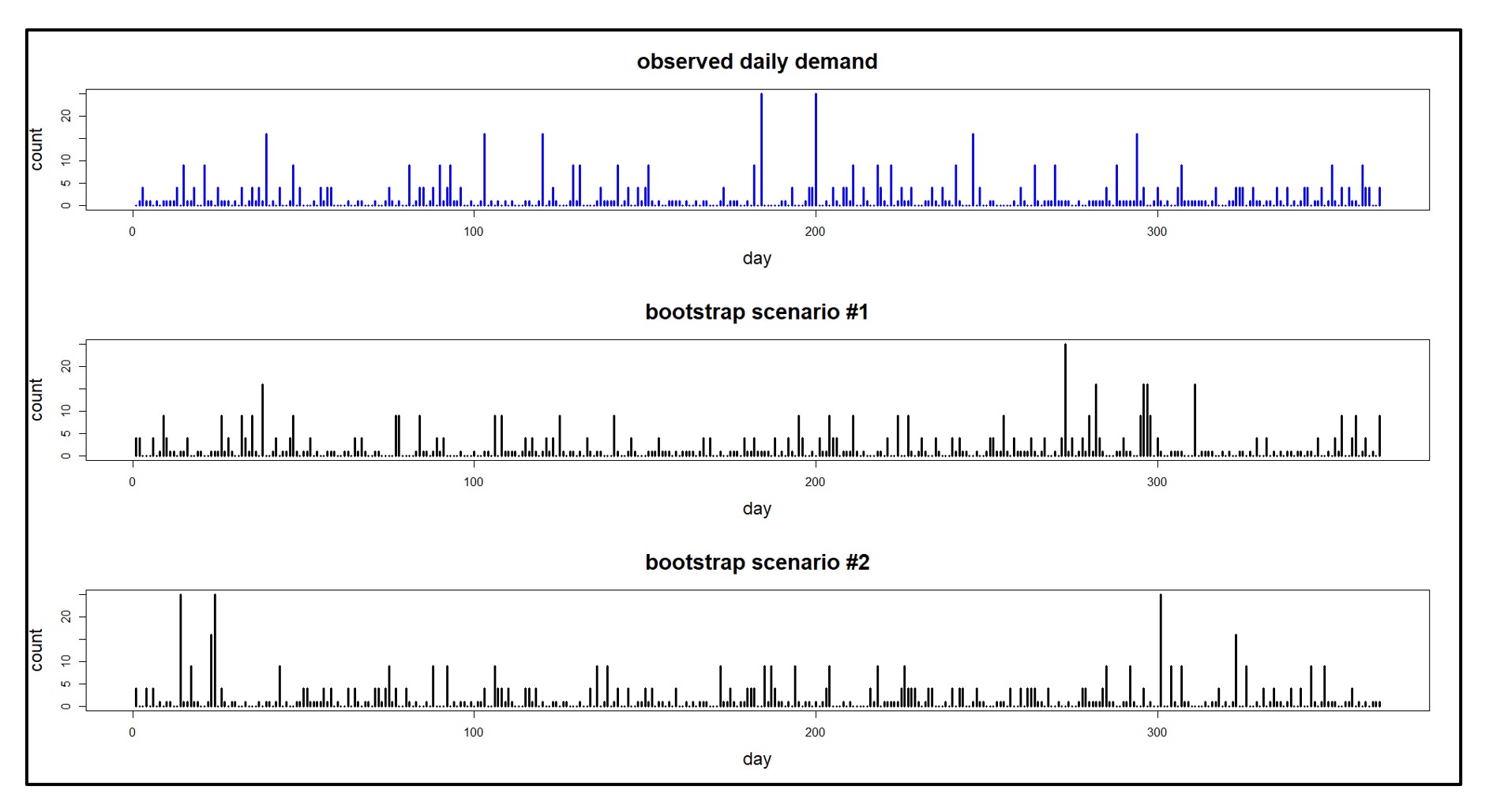
Figuur 1: Een waargenomen vraagvolgorde en daarvan afgeleide vraagscenario’s.
Figuur 2 toont twee vraagscenario's en hun gevolgen voor de voorraad in een bepaald voorraadbeheersysteem. Het verschil tussen de twee voorraadgrafieken illustreert de mate waarin de willekeur in de vraag het probleem domineert. Het bovenste plot toont twee afleveringen van stockout, terwijl het onderste plot negen toont. Door het gemiddelde te nemen over vele scenario's zullen de typische waarden van Key Performance Metrics (KPI's) worden verduidelijkt, zoals het gemiddelde aantal stockouts dat is gekoppeld aan elke keuze van het bestelpunt en de bestelhoeveelheid (die respectievelijk 10 en 25 zijn in figuur 2).
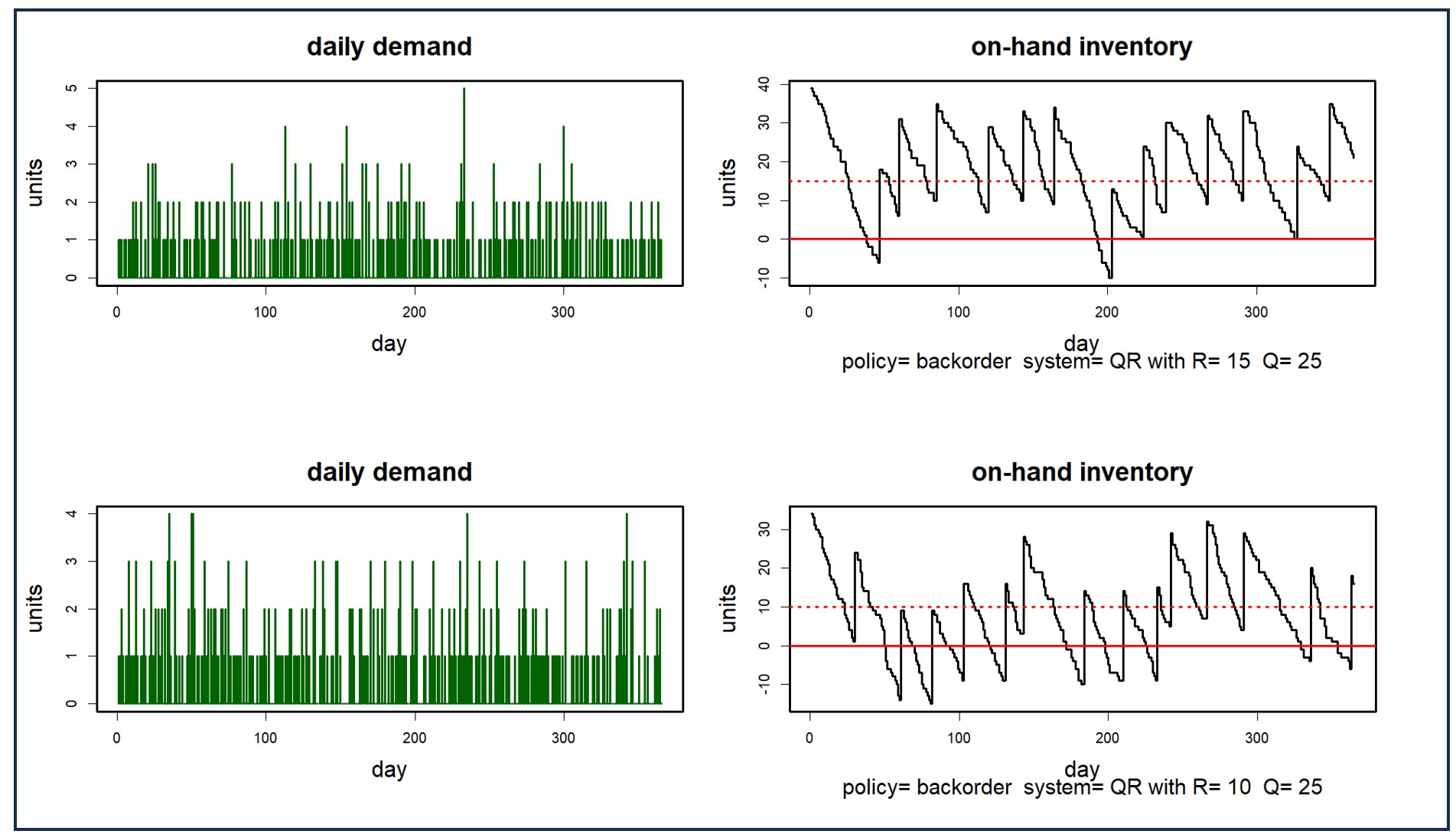
Figuur 2: Twee vraagscenario's en hun gevolgen voor de voorhanden voorraad
In deze notitie beschrijven we technieken voor het maken van scenario's en geven we criteria op voor het evalueren van scenariogeneratoren.
Criteria voor scenario's
Zoals we hieronder zullen zien, zijn er verschillende manieren om scenario's te maken. Ongeacht de bron, welke criteria definiëren een ‘goed’ scenario? Er zijn vier hoofdcriteria: trouw, variëteit, hoeveelheid en kosten. Trouw vat samen hoe nauwkeurig een scenario situaties uit de echte wereld imiteert. High-fidelity betekent dat de scenario's de werkelijke gebeurtenissen nauwkeurig weerspiegelen en een solide basis vormen voor analyse en besluitvorming. Verscheidenheid beschrijft de diversiteit aan scenario's die een generator kan creëren. Een veelzijdige generator kan een breed scala aan potentiële situaties simuleren, waardoor mogelijkheden en risico's grondig kunnen worden verkend. Hoeveelheid verwijst naar het aantal scenario's dat een generator kan produceren. Een generator die een groot aantal scenario's kan creëren, levert voldoende gegevens voor analyse. Kosten houdt rekening met zowel de computer- als de menselijke hulpbronnen die nodig zijn om de scenario's te produceren. Een efficiënte scenariogenerator brengt kwaliteit in evenwicht met het gebruik van hulpbronnen, zodat de inspanning wordt gerechtvaardigd door de waarde en nauwkeurigheid van de resultaten.
Scenariogeneratie
Denk opnieuw aan een scenario als een tijdreeks. Hoe komen scenario's tot stand?
- Gepetto's werkplaats: Deze aanpak omvat het handmatig vervaardigen van scenario's door experts. Hoewel het high-fidelity (realisme) kan opleveren, vergt het zeer veel middelen en kan het niet gemakkelijk variatie genereren, wat een groot aantal scenario's vereist.
- Groundhog-dag: Bij deze methode wordt herhaaldelijk één enkele praktijksituatie als input gebruikt. Hoewel het per definitie realistisch en kosteneffectief is (er worden geen andere middelen gebruikt dan het vastleggen van de gegevens), mist deze aanpak variatie en kan daarom de diversiteit van scenario's uit de echte wereld niet accuraat weerspiegelen.
- Parametrische modellen: Voorbeelden van parametrische modellen zijn de klassiekers die in de klassen van de Statistiek worden bestudeerd: Normaal, exponentieel, Poisson, enz. De vraagdiagrammen in Figuur 2 worden parametrisch gegenereerd, zijnde de kwadraten van willekeurige Poisson-variabelen. Deze modellen genereren een onbeperkt aantal goedkope scenario's met een goede variëteit, maar ze geven niet altijd de complexiteit van gegevens uit de echte wereld weer, waardoor de betrouwbaarheid mogelijk in gevaar komt. Wanneer de werkelijkheid ingewikkelder is, genereren deze modellen te vereenvoudigde scenario's.
- Niet-parametrische tijdreeksbootstraps: Deze aanpak kan goed scoren op alle criteria: trouw, variëteit, kwantiteit en kosten. Het is een veelzijdige methode die uitblinkt in het creëren van enorme aantallen realistische scenario's. De synthetische vraaggeschiedenissen in Figuur 1 zijn eenvoudige bootstrap-voorbeelden, gebaseerd op de waargenomen waarden in de bovenste grafiek. (Zie de onderstaande links voor enkele details over het genereren van scenario's.)
Scenario's exploiteren
Scenario's bewijzen hun waarde op twee manieren: als input voor besluitvorming en als intuïtiebouwers. Wanneer vraagscenario's bijvoorbeeld worden gebruikt als input voor simulatiemodellen, maken ze stresstests en prestatieschattingen voor systeemontwerp mogelijk. Scenario's kunnen ook dienen als intuïtiebouwers voor besluitvormers of systeembeheerders. Hun visuele weergave helpt bij het ontwikkelen van inzicht in en waardering voor de risico's die gepaard gaan met het nemen van operationele beslissingen, of het nu gaat om vraagvoorspelling of voorraadbeheer.
Scenario-gebaseerde analyse is zeer computerintensief, vooral wanneer de scenario's worden gegenereerd door middel van bootstrapping. Bij Smart Software gebeurt het rekenen in de cloud. Stel je de rekenlast voor die gepaard gaat met het bepalen van bestelpunten en bestelhoeveelheden voor elk van de tienduizenden voorraadartikelen met behulp van honderden of duizenden vraagsimulaties voor elk artikel. Stel je verder voor dat de software niet alleen een specifiek voorgesteld paar van bestelpunten en bestelhoeveelheid evalueert, maar door de hele “ontwerpruimte” van paren dwaalt om het beste paar controleparameters voor elk item te vinden. Om dit praktisch te maken, profiteren we van de parallelle verwerkingskracht van de cloud. In wezen krijgt elk inventarisitem een eigen computer toegewezen die bij de berekeningen kan worden gebruikt, zodat al dat computerwerk tegelijkertijd kan plaatsvinden in plaats van opeenvolgend. Nu kunnen we losgaan en u echt de resultaten bezorgen die u nodig heeft.
Meer leren
Wie geïnteresseerd is in verdere technische details en referenties, kan hier meer informatie vinden.
Wat maakt een probabilistische voorspelling?
Probabilistische prognoses voor intermitterende vraag




