Twee voorraadproblemen
Als je zowel dingen maakt als verkoopt, bezit je twee voorraadproblemen. Bedrijven die dingen verkopen, moeten zich onophoudelijk concentreren op het hebben van voldoende productvoorraad om aan de vraag van de klant te voldoen. Fabrikanten en activa-intensieve industrieën zoals energieopwekking, openbaar vervoer, mijnbouw en raffinage hebben een extra voorraadprobleem: voldoende reserveonderdelen hebben om hun machines draaiende te houden. In deze technische samenvatting worden de basisprincipes van twee probabilistische modellen van machinestoringen besproken. Het relateert ook de beschikbaarheid van machines aan de toereikendheid van de voorraad reserveonderdelen.
Modellering van het falen van een machine die wordt behandeld als een "zwarte doos"
Net zoals de vraag naar producten inherent willekeurig is, geldt dat ook voor de timing van machinestoringen. Evenzo, net zoals probabilistische modellering de juiste manier is om met willekeurige vraag om te gaan, is het ook de juiste manier om met willekeurige storingen om te gaan.
Modellen van machinestoringen hebben twee componenten. De eerste gaat over de willekeurige duur van uptime. De tweede gaat over de willekeurige duur van downtime.
Het veld van betrouwbaarheid theorie biedt verschillende standaard waarschijnlijkheidsmodellen die de willekeurige tijd beschrijven tot het uitvallen van een machine zonder rekening te houden met de reden voor het uitvallen. Het eenvoudigste model van uptime is de exponentiële verdeling. Dit model zegt dat de gevaar tarief, dwz de kans op falen in het volgende moment, is constant, ongeacht hoe lang het systeem in werking is. Het exponentiële model is goed in het modelleren van bepaalde soorten systemen, met name elektronica, maar het is niet universeel toepasbaar.
Download de whitepaper
De volgende stap omhoog in modelcomplexiteit is de Weibull model (uitgesproken als "WHY-bull"). De Weibull-verdeling maakt het mogelijk dat het risico van falen in de loop van de tijd verandert, ofwel afneemt na een inbrandperiode, ofwel vaker toeneemt naarmate slijtage zich ophoopt. De exponentiële verdeling is een speciaal geval van de Weibull-verdeling waarin de risicograad niet toeneemt of afneemt.
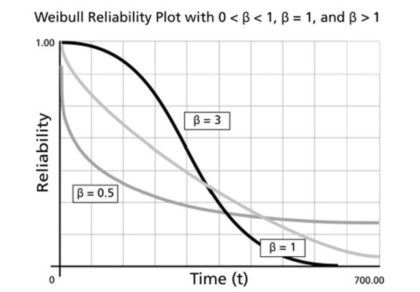
Figuur 1: Drie verschillende Weibull-overlevingscurven
Figuur 1 illustreert de waarschijnlijkheid van het Weibull-model dat een machine nog steeds draait als functie van hoe lang deze al draait. Er zijn drie curven die overeenkomen met constante, afnemende en toenemende risicopercentages. Om voor de hand liggende redenen worden deze genoemd overlevingscurven omdat ze de overlevingskans voor verschillende tijdsperioden uitzetten (maar ze worden ook wel betrouwbaarheidscurven). De zwarte curve die hoog begint en snel daalt (β=3) geeft een machine weer die met de jaren verslijt. De lichtste curve in het midden snel (β=1) toont de exponentiële verdeling. De medium-donkere curve (β=0,5) is er een die een hoog percentage vroege risico's heeft, maar beter wordt met de leeftijd.
Er is natuurlijk nog een ander fenomeen dat in de analyse moet worden meegenomen: downtime. Het modelleren van downtime is waar voorraadtheorie in beeld komt. Downtime wordt gemodelleerd door een combinatie van twee verschillende distributies. Als er een reserveonderdeel beschikbaar is om het defecte onderdeel te vervangen, kan de downtime erg kort zijn, bijvoorbeeld één dag. Maar als er geen reserve op voorraad is, kan de downtime behoorlijk lang zijn. Zelfs als de reserve snel kan worden verkregen, kan het enkele dagen of een week duren voordat de machine kan worden gerepareerd. Als het reserveonderdeel door een verre leverancier moet worden vervaardigd en over zee moet worden vervoerd en vervolgens per spoor moet worden vervoerd naar uw fabriek, kan de uitvaltijd weken of maanden zijn. Dit alles betekent dat het bijhouden van een goede inventaris van reserveonderdelen erg belangrijk is om de productie op gang te houden.
Bij dit geaggregeerde type analyse wordt de machine behandeld als een zwarte doos die werkt of niet. Hoewel de details worden genegeerd van welk onderdeel het heeft begeven en wanneer, is een dergelijk model nuttig voor het inschatten van de pool van machines die nodig is om met grote waarschijnlijkheid een minimaal niveau van productiecapaciteit te handhaven.
De binominale verdeling is het waarschijnlijkheidsmodel dat relevant is voor dit probleem. De binominale is hetzelfde model dat bijvoorbeeld de verdeling beschrijft van het aantal "koppen" dat resulteert uit twintig worpen van een munt. In het machinebetrouwbaarheidsprobleem komen de machines overeen met munten, en een resultaat van koppen komt overeen met het hebben van een werkende machine.
Als voorbeeld, als
- de kans dat een bepaalde machine op een bepaalde dag draait, is 90%
- machinestoringen zijn onafhankelijk (bijv. geen overstroming of tornado om ze allemaal in één keer weg te vagen)
- je hebt minimaal een kans van 95% nodig dat er op een bepaalde dag minstens 5 machines draaien
dan schrijft het binominale model zeven machines voor om je doel te bereiken.
Modellering van machinestoringen op basis van componentstoringen

Het Weibull-model kan ook worden gebruikt om het falen van een enkel onderdeel te beschrijven. Elke realistisch complexe productiemachine heeft echter meerdere onderdelen en heeft daarom meerdere faalwijzen. Dit betekent dat het berekenen van de tijd totdat de machine uitvalt een analyse vereist van een "race naar mislukking", waarbij elk onderdeel strijdt om de "eer" om als eerste te falen.
Als we de redelijke aanname maken dat onderdelen onafhankelijk van elkaar falen, wijst de standaardkanstheorie de weg naar het combineren van de modellen van het falen van individuele onderdelen tot een algemeen model van machinefalen. De tijd tot het eerste van vele onderdelen faalt heeft een poly-Weibull verdeling. Op dit punt kan de analyse echter behoorlijk ingewikkeld worden, en de beste stap zou kunnen zijn om over te schakelen van analyse-per-vergelijking naar analyse-per-simulatie.
Machinestoring simuleren op basis van de details van defecte onderdelen
Simulatieanalyse kreeg zijn moderne start als een spin-off van het Manhattan-project om de eerste atoombom te bouwen. De methode wordt ook vaak genoemd Monte Carlo simulatie naar het grootste gokcentrum ter wereld vroeger (vandaag zou het "Macau-simulatie" zijn).
Een simulatiemodel zet de logica van de opeenvolging van willekeurige gebeurtenissen om in overeenkomstige computercode. Vervolgens gebruikt het door de computer gegenereerde (pseudo-)willekeurige getallen als brandstof om het simulatiemodel aan te drijven. De faaltijd van elk onderdeel wordt bijvoorbeeld gemaakt door te putten uit de specifieke Weibull-faaltijdverdeling. Dan begint de vroegste van die storingstijden met de volgende episode van machinestilstand.

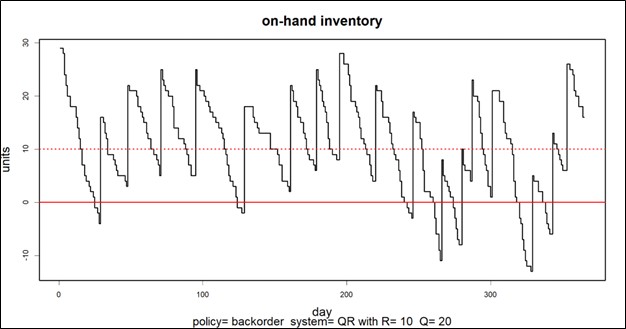
Afbeelding 2: een simulatie van de bedrijfstijd van een machine gedurende een jaar
Figuur 2 toont de resultaten van een simulatie van de uptime van een enkele machine. Machines doorlopen afwisselende periodes van uptime en downtime. In deze simulatie wordt aangenomen dat uptime een exponentiële verdeling heeft met een gemiddelde duur (MTBF = Mean Time Before Failure) van 30 dagen. Downtime heeft een 50:50 verdeling tussen 1 dag als er een reserve beschikbaar is en 30 dagen als dat niet het geval is. In de simulatie weergegeven in figuur 2 werkt de machine gedurende 85% van de dagen in één jaar in bedrijf.
Een geschatte formule voor machine-uptime
Hoewel Monte Carlo-simulatie nauwkeurigere resultaten kan opleveren, doet een eenvoudiger algebraïsch model het goed als benadering en maakt het gemakkelijker om te zien hoe de belangrijkste variabelen zich verhouden.
Definieer de volgende sleutelvariabelen:
- MTBF = Mean Time Before Failure (dagen)
- Pa = waarschijnlijkheid dat er een reserveonderdeel beschikbaar is wanneer dat nodig is
- MDTshort = Mean Down Time als er een reserve beschikbaar is wanneer dat nodig is
- MDTlong = Mean Down Time als er geen reserve beschikbaar is wanneer dat nodig is
- Uptime = Percentage dagen dat de machine in bedrijf is.
Dan is er een eenvoudige benadering voor de Uptime:
Uptime ≈ 100 x MTBF/(MTBF + MDTkort x Pa + MDTlang x (1-Pa)). (Vergelijking 1)
Vergelijking 1 vertelt ons dat de uptime afhangt van de beschikbaarheid van een reserve. Als er altijd een reserve is (Pa=1), bereikt de uptime een piekwaarde van ongeveer 100 x MTBF/(MTBF + MDTshort). Als er nooit een reserve beschikbaar is (Pa=0), bereikt de uptime de laagste waarde van ongeveer 100 x MTBF/(MTBF + MDTlong). Wanneer de reparatietijd ongeveer net zo lang is als de normale tijd tussen storingen, zakt de uptime naar een onaanvaardbaar niveau in de buurt van 50%. Als er altijd een reserve beschikbaar is, kan de uptime de 100% benaderen.
Het relateren van machinestilstand aan de inventaris van reserveonderdelen
Het minimaliseren van uitvaltijd vereist een meervoudig initiatief met intensieve training van de machinist, gebruik van hoogwaardige grondstoffen, effectief preventief onderhoud en adequate reserveonderdelen. De eerste drie stellen de voorwaarden voor goede resultaten. De laatste gaat over onvoorziene omstandigheden.

Als een machine eenmaal uitvalt, vliegt het geld de deur uit en is er een premie om het snel weer op gang te krijgen. Deze scène kan zich op twee manieren afspelen. De goede heeft een reserveonderdeel klaarliggen, zodat de uitvaltijd tot een minimum kan worden beperkt. De slechte heeft geen reserveonderdelen beschikbaar, dus er is een strijd om de levering van het benodigde onderdeel te bespoedigen. In dit geval moet de fabrikant zowel de kosten van verloren productie als de kosten van versnelde verzending dragen, als dat al een optie is.
Als het voorraadsysteem goed is ontworpen, zal de beschikbaarheid van reserveonderdelen geen grote belemmering vormen voor de inzetbaarheid van de machine. Met het ontwerp van een voorraadsysteem bedoel ik de resultaten van verschillende keuzes: of het tekortbeleid een nabestellingsbeleid of een verliesbeleid is, of de inventarisatiecyclus periodiek of continu is, en welke bestelpunten en bestelhoeveelheden worden vastgesteld.
Wanneer voorraadbeleid voor producten wordt ontworpen, worden ze beoordeeld aan de hand van verschillende criteria. Serviceniveau is het percentage van de bevoorradingsperioden dat verstrijkt zonder dat er sprake is van voorraaduitval. Fill Rate is het percentage bestelde eenheden dat direct uit voorraad wordt geleverd. Het gemiddelde voorraadniveau is het typische aantal beschikbare eenheden.
Geen van deze is precies de maatstaf die nodig is voor de opslag van reserveonderdelen, hoewel ze allemaal gerelateerd zijn. De benodigde maatstaf is Artikelbeschikbaarheid, het percentage dagen waarin er ten minste één reserve klaar is voor gebruik. Hogere serviceniveaus, opvullingspercentages en voorraadniveaus impliceren allemaal een hoge itembeschikbaarheid en er zijn manieren om van de ene naar de andere om te schakelen. (Wanneer meerdere machines dezelfde voorraad reserveonderdelen delen, wordt voorraadbeschikbaarheid vervangen door de waarschijnlijkheidsverdeling van het aantal reserveonderdelen op een bepaalde dag. We laten dat complexere probleem voor een andere dag liggen.)
Het is duidelijk dat het aanhouden van een goede voorraad reserveonderdelen de kosten van machinestilstand vermindert. Natuurlijk zorgt het aanhouden van een goede voorraad reserveonderdelen voor eigen voorraad- en bestelkosten. Dit is het tweede voorraadprobleem van de fabrikant. Zoals bij elke beslissing met betrekking tot inventaris, is het belangrijk om de juiste balans te vinden tussen deze twee concurrerende kostenplaatsen. Zien dit artikel over probabilistische prognoses voor intermitterende vraag voor begeleiding bij het vinden van dat evenwicht.