De slimme voorspeller

Denk aan het probleem van het aanvullen van de voorraad. Stel dat het betreffende voorraadartikel een reserveonderdeel is, om precies te zijn. Zowel u als uw leverancier zullen een idee willen hebben van hoeveel u gaat bestellen en wanneer. En uw ERP-systeem dringt er misschien op aan dat u ook het geheim prijsgeeft.
Deterministisch model van aanvulling
De eenvoudigste manier om een fatsoenlijk antwoord op deze vraag te krijgen, is aan te nemen dat de wereld, nou ja, eenvoudig is. In dit geval betekent eenvoudig 'niet willekeurig' of, in nerdtaal, 'deterministisch'. In het bijzonder doe je alsof de willekeurige grootte en timing van de vraag in werkelijkheid een continue druppel-druppel-druppel is van een vaste grootte die met een vast interval komt, bijvoorbeeld 2, 2, 2, 2, 2, 2... Als dit onrealistisch lijkt , het is. De echte vraag ziet er misschien meer zo uit: 0, 1, 10, 0, 1, 0, 0, 0 met veel nullen, af en toe maar willekeurige pieken.
Maar eenvoud heeft zijn deugden. Als je net doet alsof de gemiddelde vraag elke dag op rolletjes loopt, is het gemakkelijk om uit te rekenen wanneer je je volgende bestelling moet plaatsen en hoeveel eenheden je nodig hebt. Stel dat uw voorraadbeleid van het type (Q,R) is, waarbij Q een vaste bestelhoeveelheid is en R een vast bestelpunt. Wanneer de voorraad daalt tot of onder het bestelpunt R, bestelt u Q-eenheden meer. Om de fantasie compleet te maken, gaan we ervan uit dat de doorlooptijd voor aanvulling ook vast is: na L dagen zullen die Q nieuwe eenheden op de plank liggen, klaar om aan de vraag te voldoen.
Alles wat u nu nodig heeft om uw vragen te beantwoorden, is de gemiddelde vraag per dag D naar het artikel. De logica gaat als volgt:
- U begint elke aanvullingscyclus met Q-eenheden bij de hand.
- Je put die voorraad uit met D eenheden per dag.
- U bereikt dus het bestelpunt R na (QR)/D dagen.
- Je bestelt dus elke (QR)/D dagen.
- Elke aanvullingscyclus duurt (QR)/D + L dagen, dus u maakt in totaal 365D/(Q-R+LD) bestellingen per jaar.
- Zolang de doorlooptijd L < R/D is, zult u nooit een voorraad hebben en zal uw voorraad zo klein mogelijk zijn.
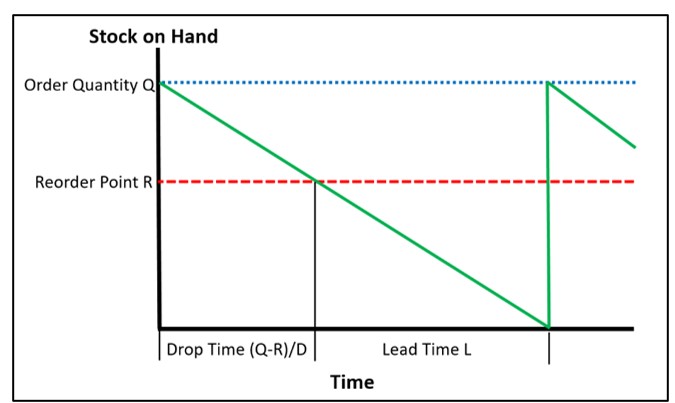
Afbeelding 1 toont de grafiek van voorhanden voorraad versus tijd voor het deterministische model. Rond Smart Software verwijzen we naar deze plot als de "Deterministische zaagtand". De voorraad begint op het niveau van de laatste bestelhoeveelheid Q. Na gestaag afnemen gedurende de uitvaltijd (QR)/D, bereikt het niveau het bestelpunt R en activeert een bestelling voor nog een Q-eenheden. Gedurende de doorlooptijd L daalt de voorraad tot precies nul, dan komt de nieuwe bestelling op magische wijze aan en begint de volgende cyclus.
Dit model heeft twee voordelen. Het vereist niet meer dan algebra van de middelbare school en het combineert (bijna) alle relevante factoren om de twee gerelateerde vragen te beantwoorden: wanneer moeten we de volgende bestelling plaatsen? Hoeveel bestellingen plaatsen we in een jaar?
Probabilistisch model van aanvulling
Het is niet verrassend dat als we een deel van de fantasie uit het deterministische model halen, we meer bruikbare informatie krijgen. Het probabilistische model omvat alle rommelige willekeur in het echte probleem: de onzekerheid in zowel de timing als de omvang van de vraag, de variatie in de doorlooptijd van de aanvulling en de gevolgen van die twee factoren: de kans dat de beschikbare voorraad de nabestelling onderschrijdt punt, de kans dat er een stockout zal zijn, de variabiliteit in de tijd tot de volgende bestelling, en het variabele aantal uitgevoerde bestellingen in een jaar.
Het probabilistische model werkt door de gevolgen van onzekere vraag en variabele doorlooptijd te simuleren. Door de historische vraagpatronen van het item te analyseren (en waarnemingen uit te sluiten die zijn geregistreerd in een tijd waarin de vraag mogelijk fundamenteel anders was), creëren geavanceerde statistische methoden een onbeperkt aantal realistische vraagscenario's. Vergelijkbare analyse wordt toegepast op records van doorlooptijden van leveranciers. Door deze vraag- en aanbodscenario's te combineren met de operationele regels van een bepaald voorraadbeheerbeleid, ontstaan scenario's van het aantal beschikbare onderdelen. Uit deze scenario's kunnen we samenvattingen halen van de variërende intervallen tussen bestellingen.
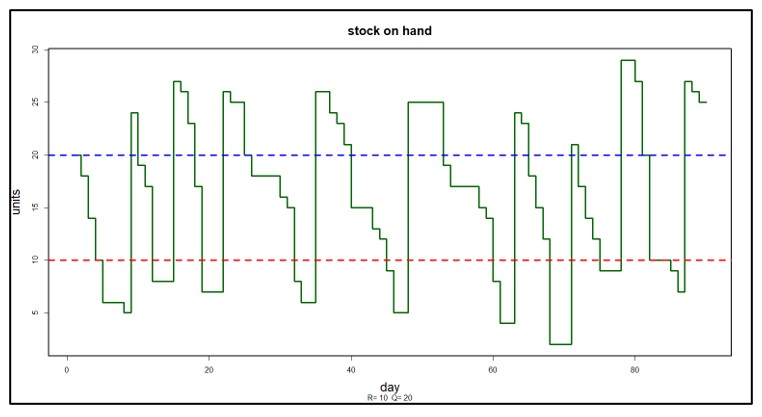
Figuur 2 toont een voorbeeld van een probabilistisch scenario; de vraag is willekeurig en het artikel wordt beheerd met bestelpunt R = 10 en bestelhoeveelheid Q=20. Voorbij is de deterministische zaagtand; in plaats daarvan is er iets complexer en realistischer (de probabilistische trap). Tijdens de 90 gesimuleerde werkingsdagen werden er 9 bestellingen geplaatst en de tijd tussen de bestellingen varieerde duidelijk.
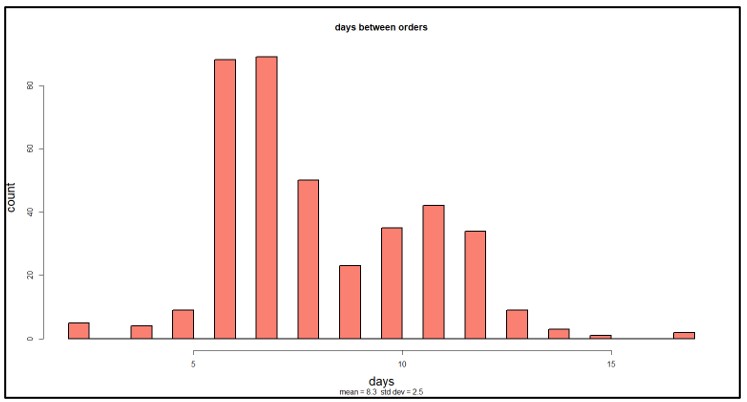
Met behulp van het probabilistische model worden de antwoorden op de twee vragen (hoe lang tussen orders en hoeveel in een jaar) uitgedrukt als kansverdelingen die de relatieve waarschijnlijkheid van verschillende scenario's weerspiegelen. Figuur 3 toont de verdeling van het aantal dagen tussen orders na tien jaar gesimuleerde werking. Hoewel het gemiddelde ongeveer 8 dagen is, varieert het werkelijke aantal sterk, van 2 tot 17.
In plaats van uw leverancier te vertellen dat u volgend jaar X bestellingen zult plaatsen, kunt u nu X ± Y bestellingen projecteren, en uw leverancier kent de opwaartse en neerwaartse risico's beter. Beter nog, u kunt de volledige distributie als het meest uitgebreide antwoord geven.
De willekeurige trap beklimmen naar grotere efficiëntie
Door verder te gaan dan het deterministische inventarismodel, ontstaan nieuwe mogelijkheden voor het optimaliseren van de bedrijfsvoering. Ten eerste maakt het probabilistische model een realistische beoordeling van het voorraadrisico mogelijk. Het eenvoudige model in afbeelding 1 houdt in dat er nooit een stockout is, terwijl probabilistische scenario's de mogelijkheid toestaan (hoewel er in afbeelding 2 slechts één close call was rond dag 70). Zodra het risico bekend is, kan software optimaliseren door de "ontwerpruimte" (dwz alle mogelijke waarden van R en Q) te doorzoeken om een ontwerp te vinden dat voldoet aan een doelniveau van voorraadrisico tegen minimale kosten. De waarde van het deterministische model in deze meer realistische analyse is dat het een goed startpunt biedt voor de zoektocht door de ontwerpruimte.
Overzicht
Moderne software geeft antwoord op operationele vragen met verschillende gradaties van detail. Aan de hand van het voorbeeld van de tijd tussen aanvullingsorders hebben we laten zien dat het antwoord bij benadering maar snel kan worden berekend met een eenvoudig deterministisch model. Maar het kan ook veel gedetailleerder worden weergegeven, waarbij alle variabiliteit wordt blootgelegd door een probabilistisch model. Wij beschouwen deze alternatieven als complementair. Het deterministische model bundelt alle sleutelvariabelen in een gemakkelijk te begrijpen vorm. Het probabilistische model biedt extra realisme dat professionals verwachten en ondersteunt effectief zoeken naar optimale keuzes van bestelpunt en bestelhoeveelheid.
Dagelijkse vraagscenario's
In deze videoblog leggen we uit hoe tijdreeksvoorspellingen naar voren zijn gekomen als een cruciaal hulpmiddel, vooral op dagelijks niveau, waarmee Smart Software sinds de oprichting ruim veertig jaar geleden pionierde. De evolutie van bedrijfspraktijken van jaarlijkse naar meer verfijnde temporele stappen zoals maandelijkse en nu dagelijkse data-analyse illustreert een significante verschuiving in operationele strategieën.

Onregelmatige operaties
Deze blog gaat over ‘onregelmatige handelingen’. Smart Software is bezig met het aanpassen van onze producten om u te helpen omgaan met uw eigen onregelmatige werkzaamheden. Dit is een voorproefje.

Vind uw plek op de voorraadafwegingscurve
Deze videoblog bevat essentiële inzichten voor degenen die werken met de complexiteit van voorraadbeheer. De sessie richt zich op het vinden van het juiste evenwicht binnen de voorraadafwegingscurve en nodigt kijkers uit om het diepgewortelde belang van dit evenwicht te begrijpen.