Sommige bedrijven investeren in software om hen te helpen hun voorraad te beheren, of het nu gaat om reserveonderdelen of eindproducten. Maar een verrassend aantal anderen speelt elke dag het Inventory Guessing Game, vertrouwend op een ingebeelde “Golden Gut” of op gewoon geluk om hun inventariscontroleparameters in te stellen. Maar wat voor resultaten verwacht je met die aanpak?
Hoe goed bent u in het aanvoelen van de juiste waarden? In deze blogpost wordt u uitgedaagd om de beste Min- en Max-waarden voor een notioneel voorraaditem te raden. We laten u de vraaggeschiedenis zien, geven u een paar relevante feiten, waarna u Min- en Max-waarden kunt kiezen en zien hoe goed ze zouden werken. Klaar?
De uitdaging
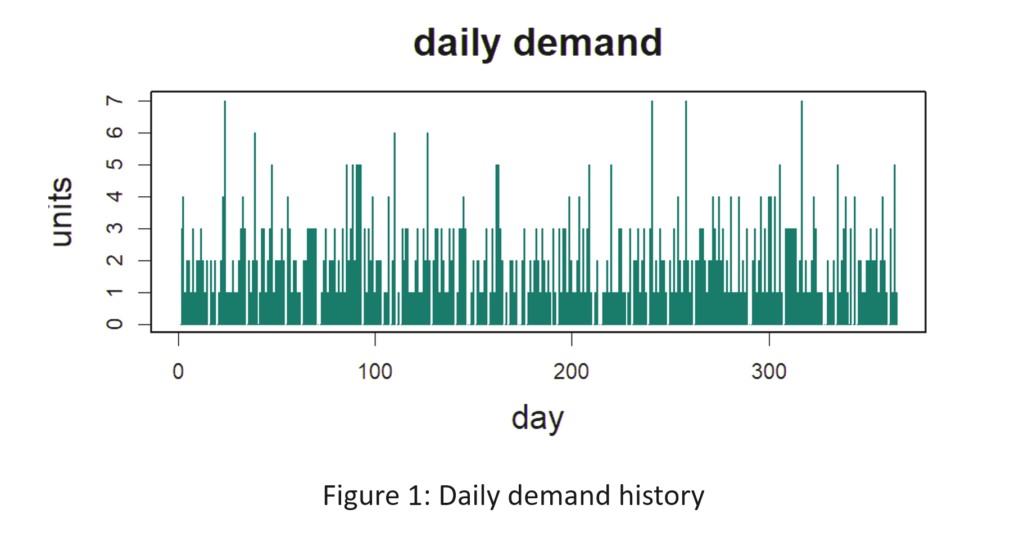
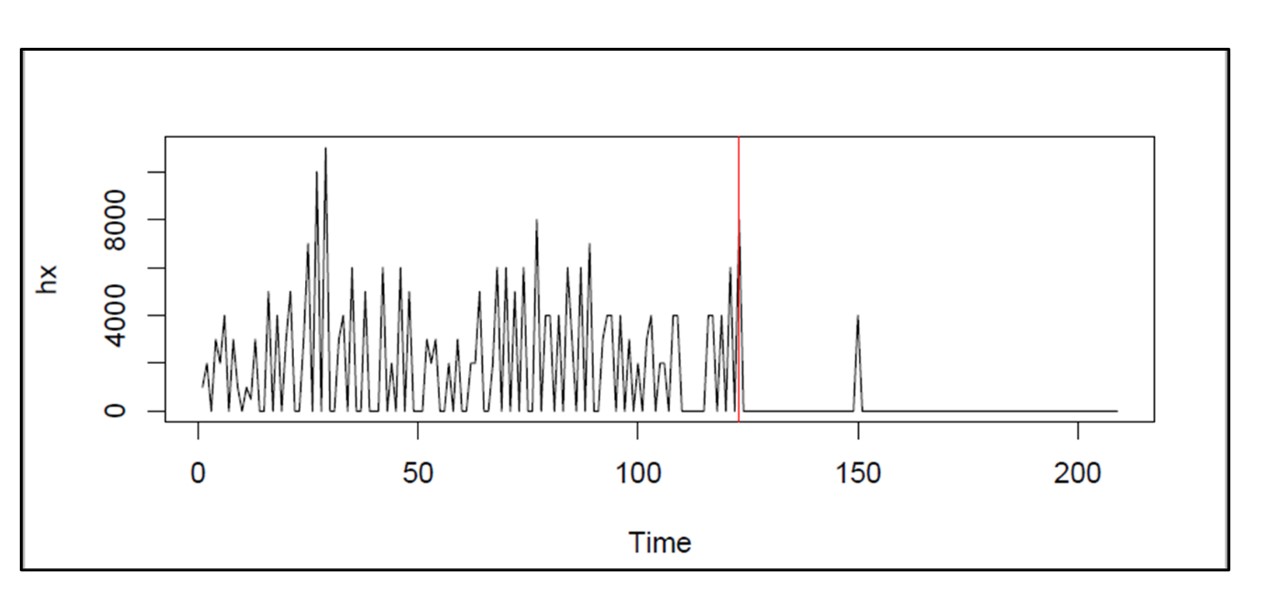
Figuur 1 toont de dagelijkse vraaggeschiedenis van het artikel. De gemiddelde vraag bedraagt 2 eenheden per dag. De doorlooptijd voor het aanvullen is constant 10 dagen (wat onrealistisch is maar in uw voordeel werkt). Bestellingen die niet direct uit voorraad leverbaar zijn, kunnen niet worden nabesteld en gaan verloren. U wilt minimaal een opvullingspercentage van 80% bereiken, maar niet tegen elke prijs. U wilt ook het gemiddelde aantal beschikbare eenheden minimaliseren en toch een opvullingspercentage van ten minste 80% bereiken. Welke Min- en Max-waarden zouden een 80%-opvullingspercentage opleveren met het laagste gemiddelde aantal beschikbare eenheden? [Neem uw antwoorden op, zodat u ze later kunt controleren. De oplossing staat hieronder aan het einde van het artikel.]
Berekening van de beste min- en max-waarden
De manier om de beste waarden te bepalen is door een digitale tweeling te gebruiken, ook wel een Monte Carlo-simulatie genoemd. De analyse creëert een groot aantal vraagscenario's en passeert deze door de wiskundige logica van het voorraadbeheersysteem om te zien welke waarden zullen worden overgenomen door de belangrijkste prestatie-indicatoren (KPI's).
We hebben voor dit probleem een digitale tweeling gebouwd en deze systematisch getest met 1.085 paar Min- en Max-waarden. Voor elk paar hebben we in totaal 100 keer 365 bedrijfsdagen gesimuleerd. Vervolgens hebben we het gemiddelde van de resultaten genomen om de prestaties van het Min/Max-paar te beoordelen in termen van twee KPI's: opvullingspercentage en gemiddelde voorraad.
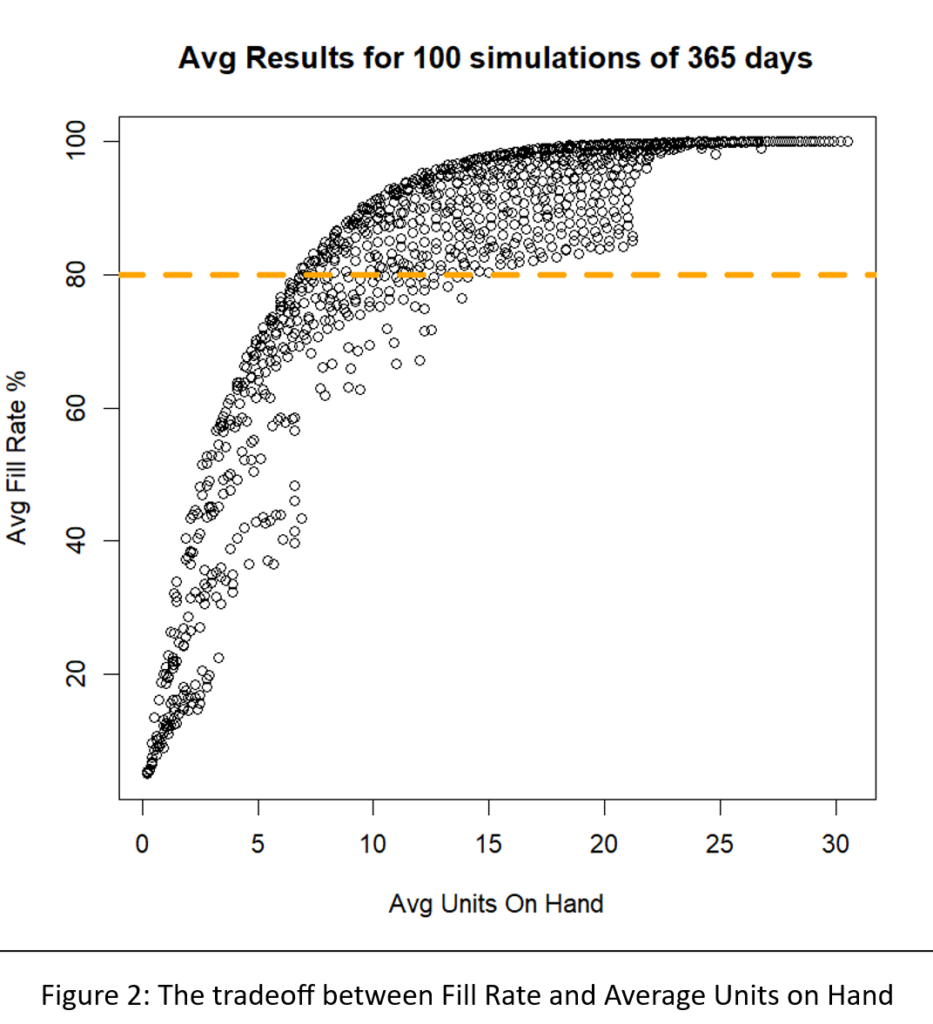
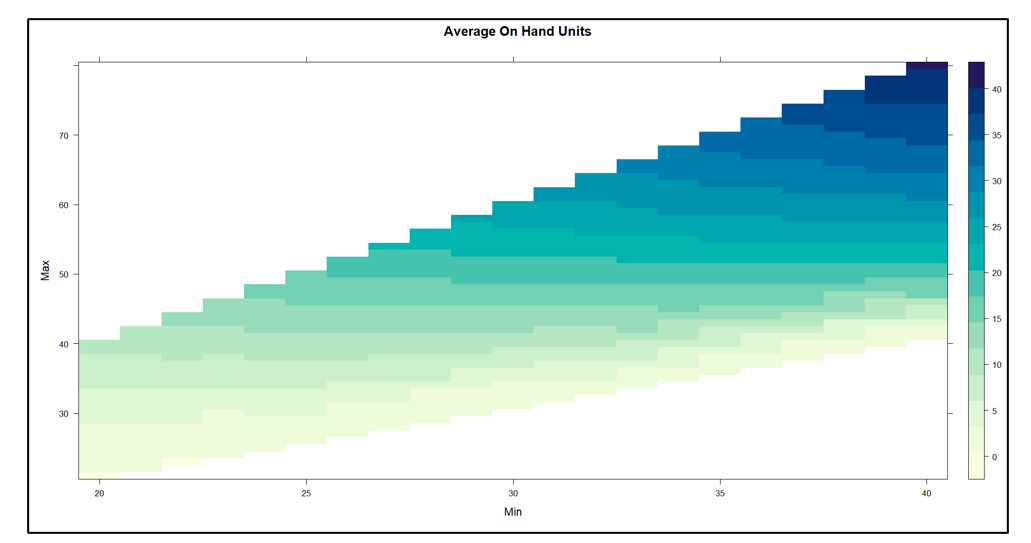
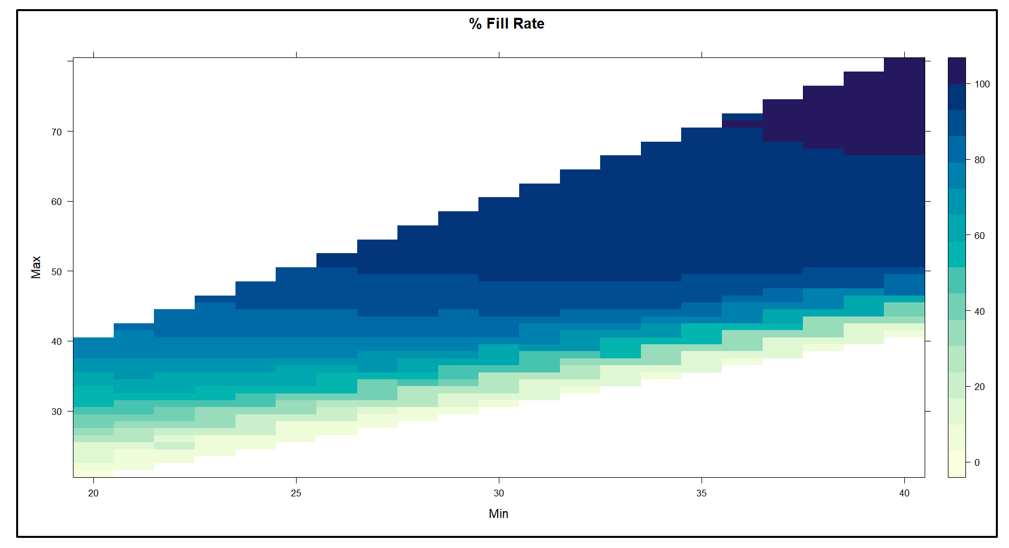
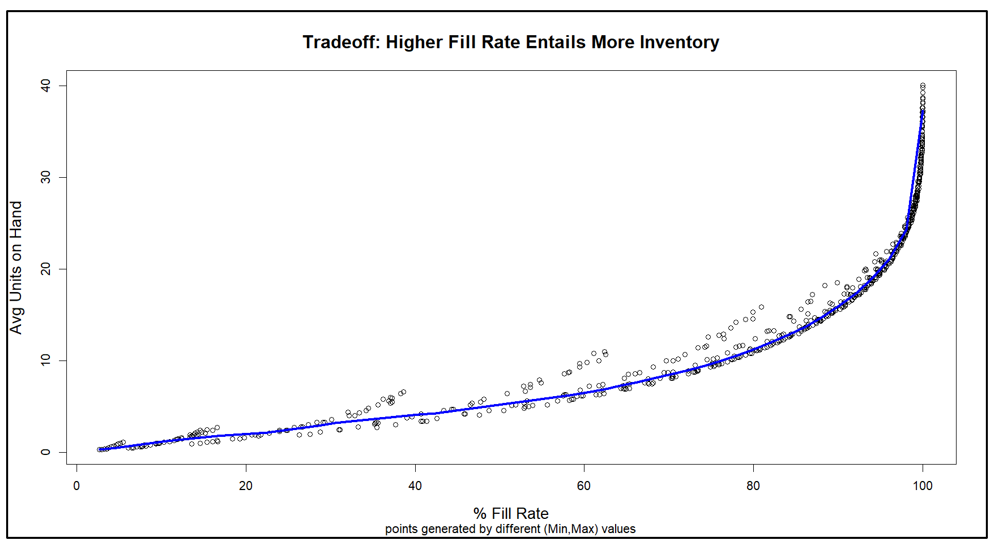
Figuur 2 toont de resultaten. De inherente afweging tussen voorraadomvang en opvullingspercentage is duidelijk in de figuur: als je een hoger opvullingspercentage wilt, moet je een grotere voorraad accepteren. Op elk inventarisniveau is er echter een bereik aan opvullingspercentages, dus het is de bedoeling om het Min/Max-paar te vinden dat het hoogste opvullingspercentage oplevert voor een inventaris van een bepaalde grootte.
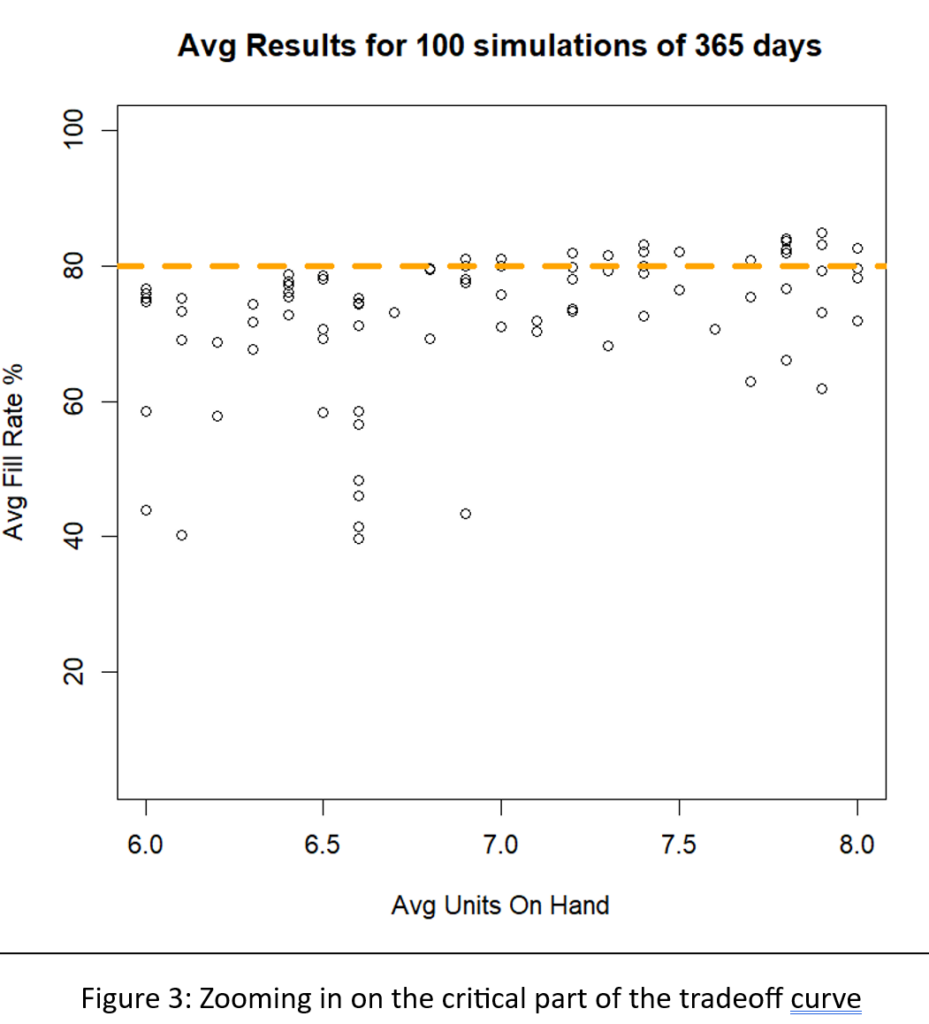
Een andere manier om Figuur 2 te interpreteren is door te focussen op de groene stippellijn die het beoogde 80%-opvullingspercentage aangeeft. Er zijn veel Min/Max-paren die in de buurt van het 80%-doel kunnen raken, maar ze verschillen qua voorraadgrootte van ongeveer 6 tot ongeveer 8 eenheden. Figuur 3 zoomt in op dat gebied van Figuur 2 en toont een behoorlijk aantal Min/Max-paren die competitief zijn.
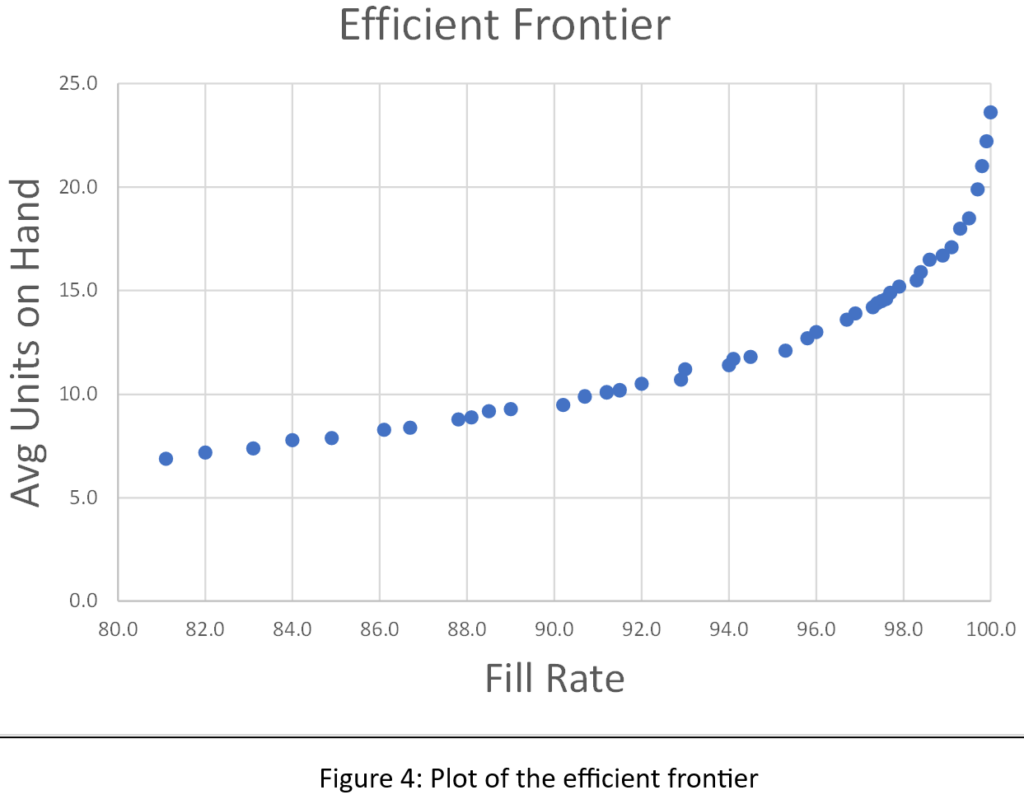
We hebben de resultaten van alle 1.085 simulaties gesorteerd om te identificeren wat economen de efficiënte grens noemen. De efficiënte grens is de reeks meest efficiënte Min/Max-paren om de wisselwerking tussen opvullingspercentage en aanwezige eenheden te benutten. Dat wil zeggen, het is een lijst met Min/Max-paren die de goedkoopste manier bieden om elk gewenst opvullingspercentage te bereiken, niet alleen 80%. Figuur 4 toont de efficiënte grens voor dit probleem. Van links naar rechts kunt u de laagste prijs aflezen die u zou moeten betalen (gemeten aan de hand van de gemiddelde voorraadgrootte) om het beoogde opvullingspercentage te bereiken. Om bijvoorbeeld een opvullingspercentage van 90% te bereiken, zou u een gemiddelde voorraad van ongeveer 10 eenheden moeten hebben.
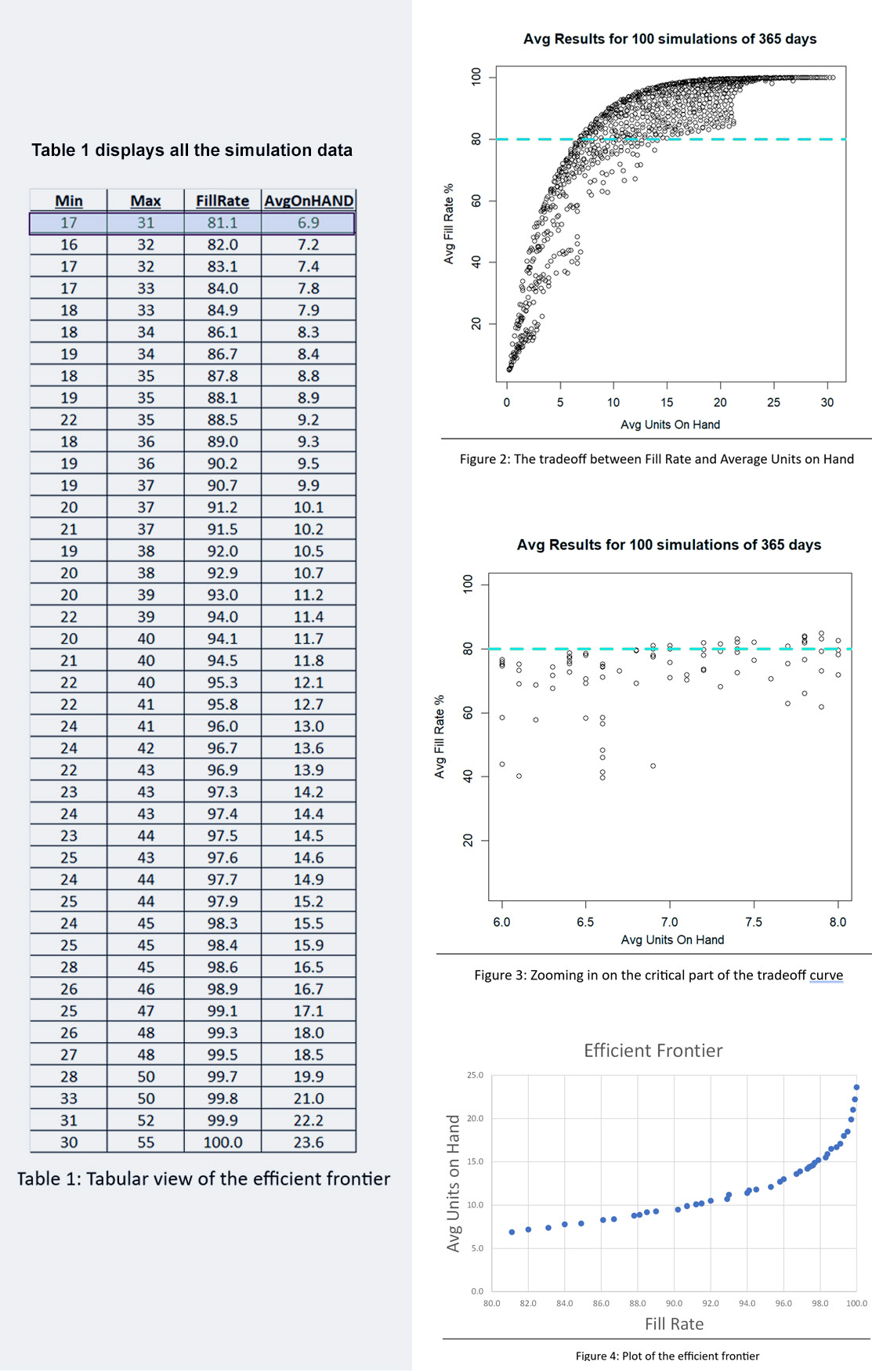
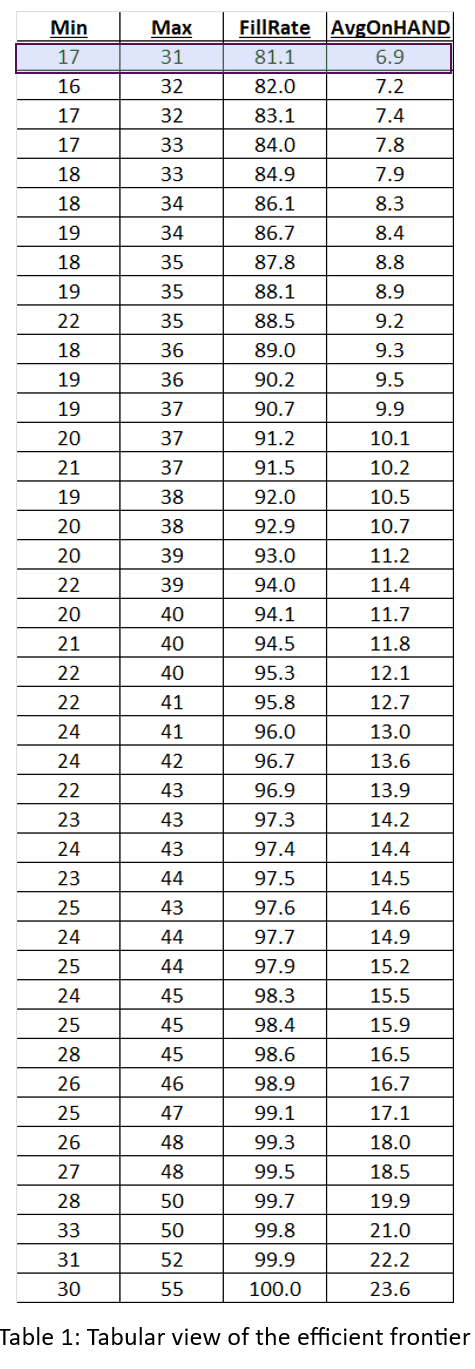
Figuren 2, 3 en 4 tonen resultaten voor verschillende Min/Max-paren, maar geven niet de waarden van Min en Max achter elk punt weer. Tabel 1 toont alle simulatiegegevens: de waarden van Min, Max, gemiddelde beschikbare eenheden en opvullingspercentage. Het antwoord op het raadspel is gemarkeerd in de eerste regel van de tabel: Min=7 en Max=131. Heb je het juiste antwoord gekregen, of iets dat in de buurt komt?2? Heb je misschien de efficiënte grens bereikt?
Conclusies
Misschien heb je geluk gehad, of misschien heb je inderdaad een Gouden Darm, maar de kans is groter dat je niet het juiste antwoord hebt gekregen, en nog waarschijnlijker dat je het niet eens hebt geprobeerd. Het vinden van het juiste antwoord is buitengewoon moeilijk zonder de digitale tweeling te gebruiken. Raden is onprofessioneel.
Een stap verder dan raden is ‘raden en zien’, waarbij u uw gok implementeert en vervolgens een tijdje (maanden?) wacht om te zien of de resultaten u bevallen. Die tactiek is op zijn minst ‘wetenschappelijk’, maar inefficiënt.
Denk nu eens aan de moeite om de beste (Min,Max) paren voor duizenden items te bepalen. Op die schaal is er zelfs nog minder reden om het inventarisraadspel te spelen. Het juiste antwoord is om het te spelen… Slim3.
1 Dit antwoord heeft een bonus, omdat het een opvullingspercentage van iets meer dan 80% behaalt bij een lagere gemiddelde voorraadgrootte dan de Min/Max-combinatie die precies 80% bereikte. Met andere woorden: (7,13) bevindt zich op de efficiënte grens.
2 Omdat deze resultaten afkomstig zijn van een simulatie in plaats van een exacte wiskundige vergelijking, is er een bepaalde foutmarge verbonden aan elk geschat opvullingspercentage en voorraadniveau. Omdat de gemiddelde resultaten echter gebaseerd waren op 100 simulaties over een periode van 365 dagen, zijn de foutmarges echter klein. Over alle experimenten heen waren de gemiddelde standaardfouten in het opvullingspercentage en de gemiddelde voorraad respectievelijk slechts 0,009% en 0,129 eenheden.
3 Mocht je dit nog niet weten: een van de oprichters van Smart Software was … Charlie Smart.