“Zakendoen is oorlog” is misschien een overdreven metafoor, maar het is niet zonder geldigheid. Net als de ‘Bomber Gap’ en de ‘Missile Gap’ liggen de zorgen om achterop te raken bij de concurrentie, en de daaruit voortvloeiende dreiging van vernietiging, altijd op de loer in de hoofden van bedrijfsleiders. Als ze dat niet doen, moeten ze dat doen, want niet alle gaten zijn denkbeeldig (de Bomber Gap en de Missile Gap bleken niet te bestaan tussen de VS en de USSR, maar de kloof tussen de Japanse en Amerikaanse productiviteit in de jaren tachtig was maar al te reëel). Het verschil tussen paranoia en gerechtvaardigde bezorgdheid is het omzetten van angst in feiten. Dit bericht gaat over het organiseren van uw aandacht voor mogelijke hiaten in de supply chain-analyses van uw bedrijf.

Hiaten in het toezicht

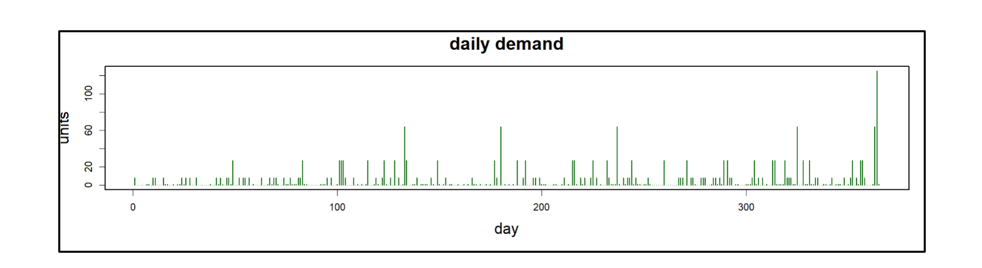
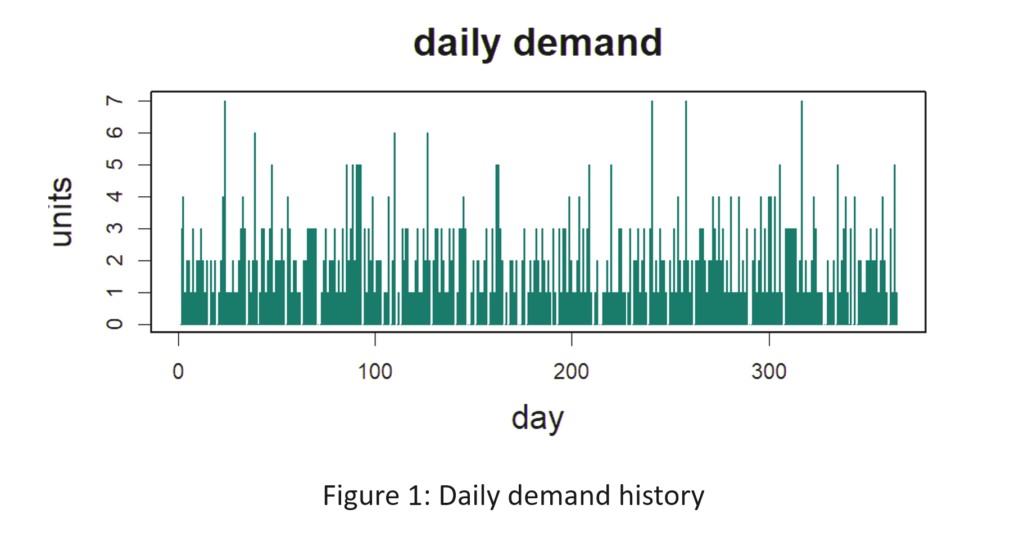
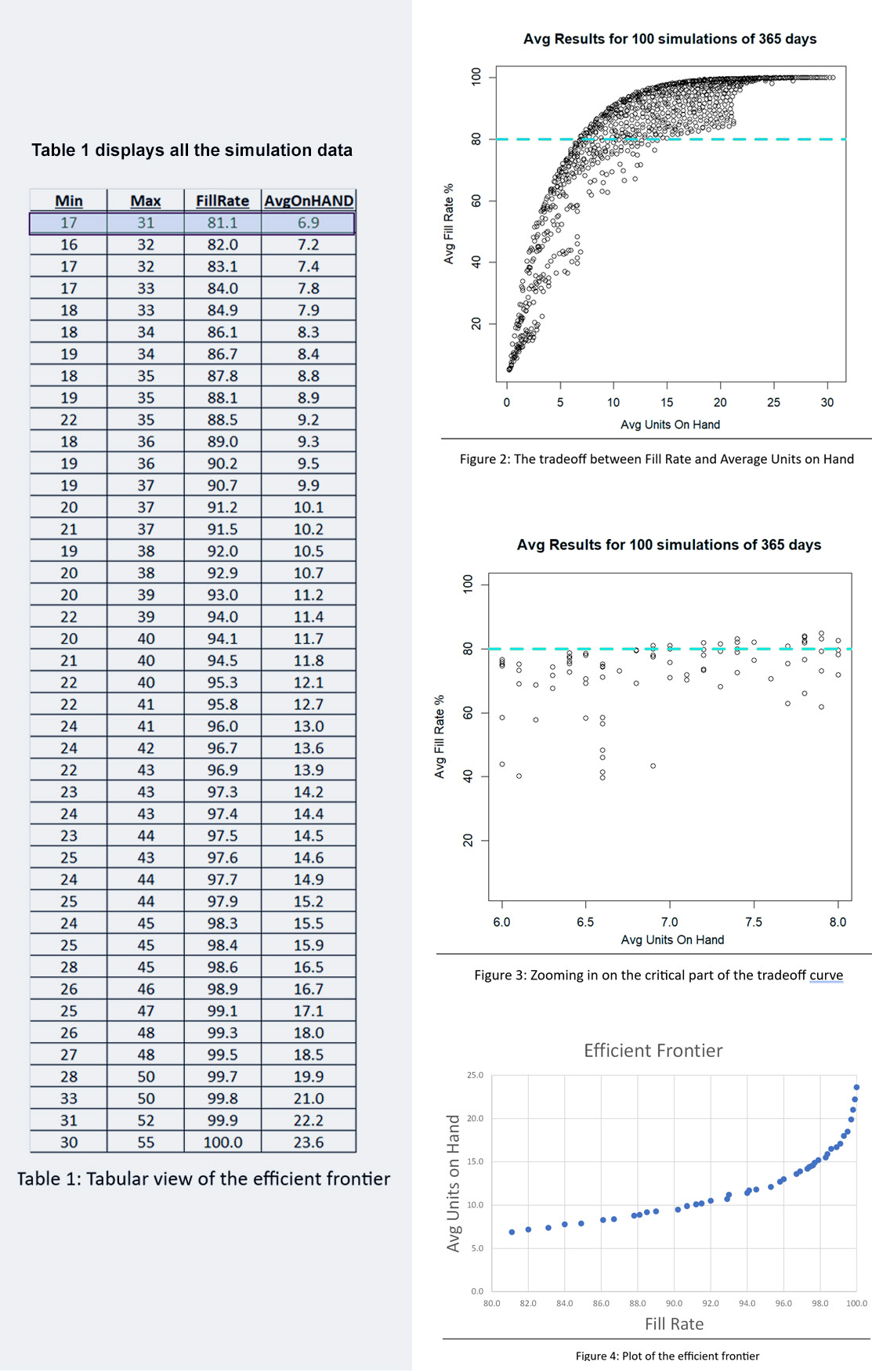
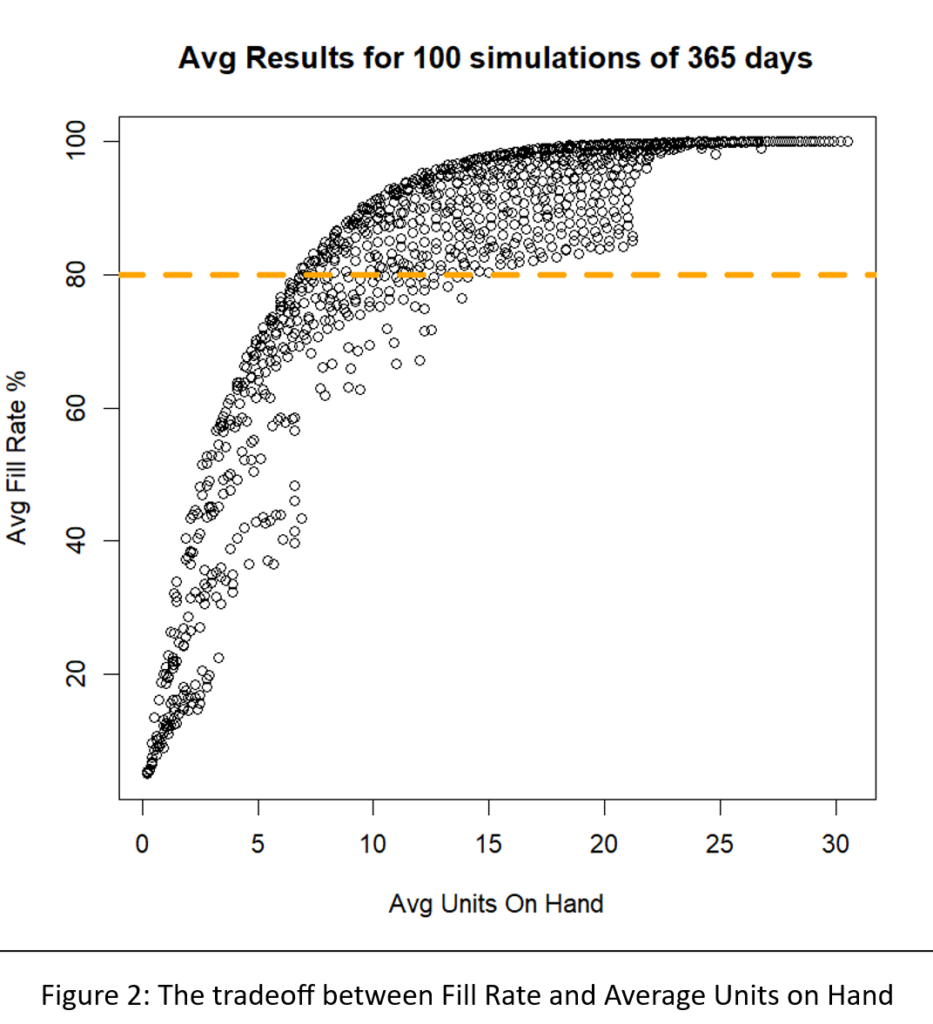
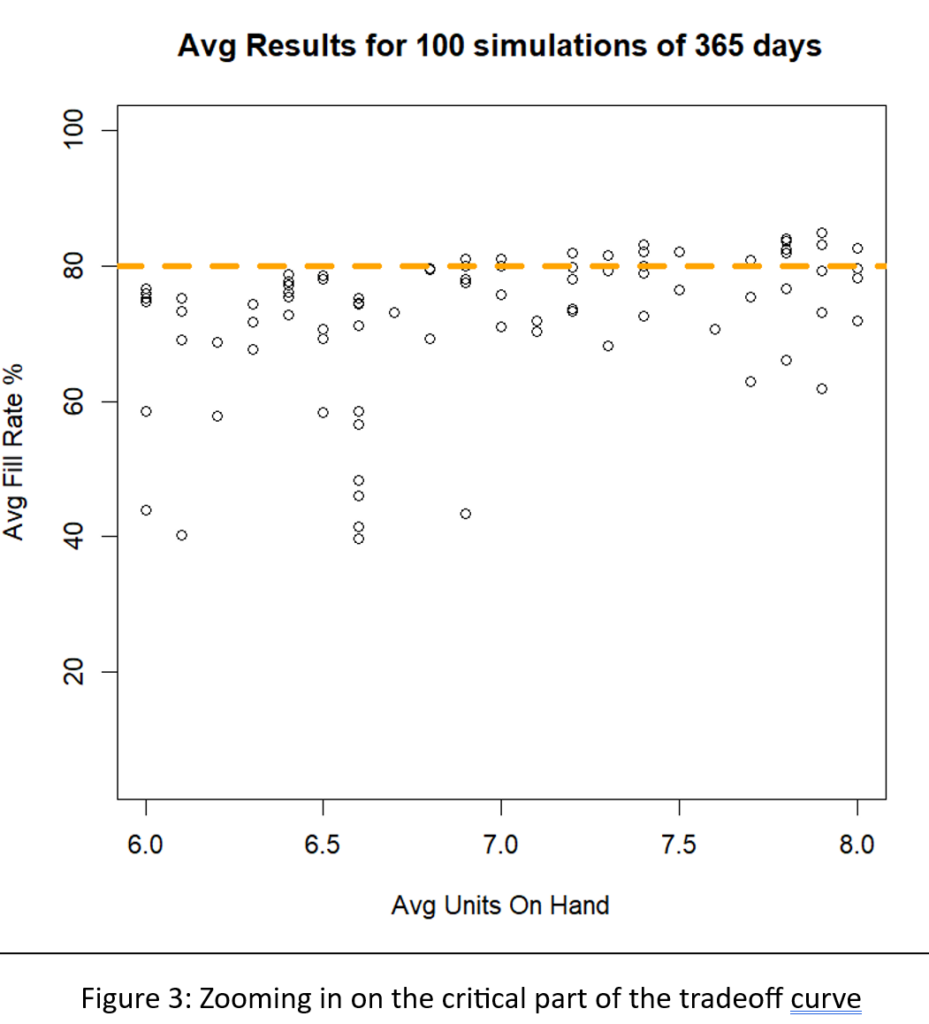
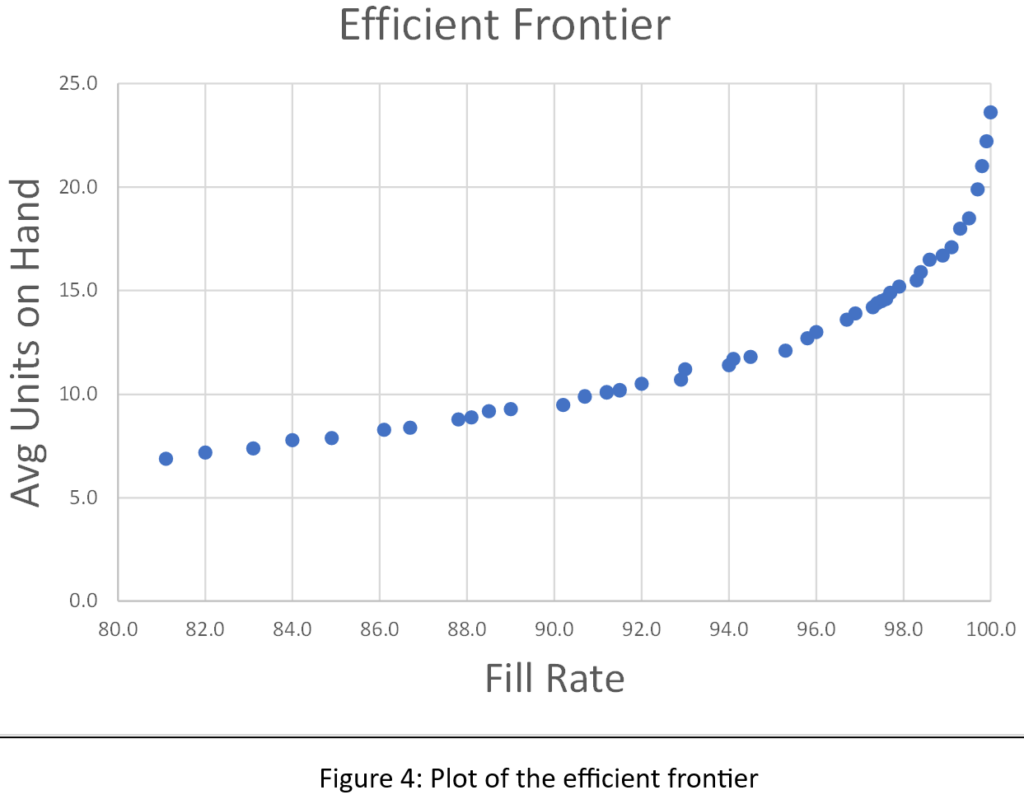
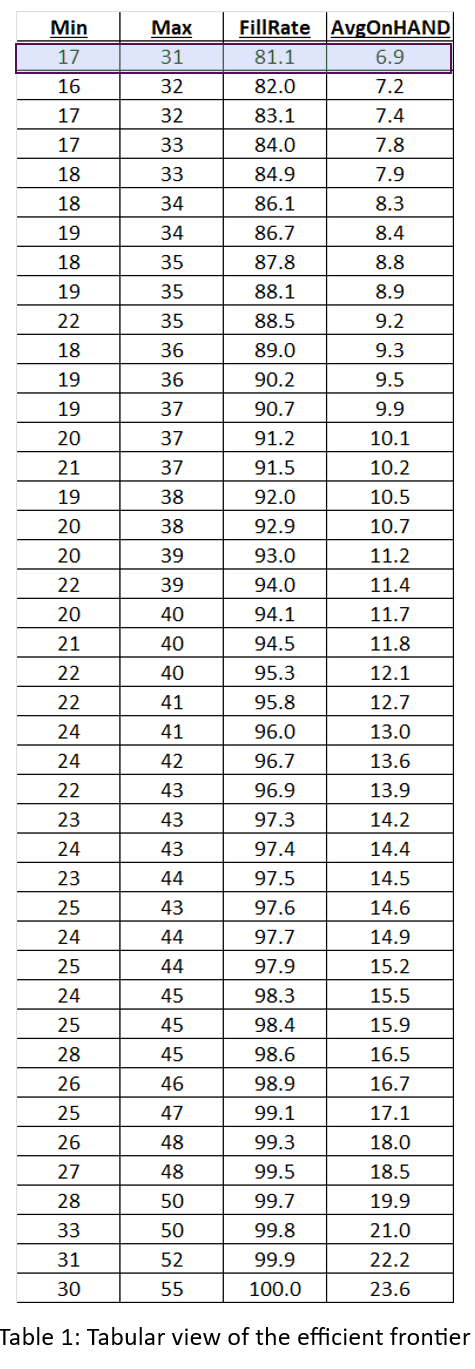
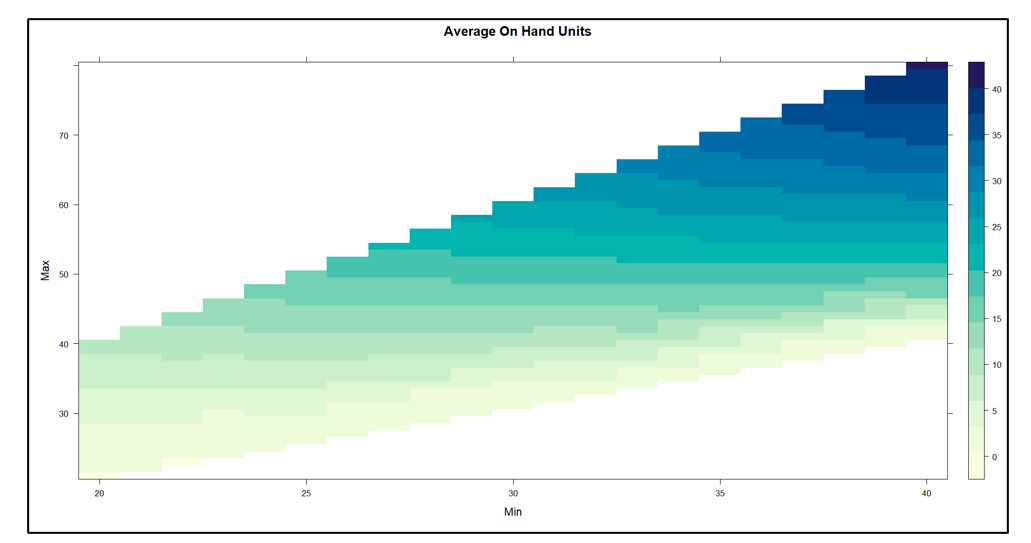
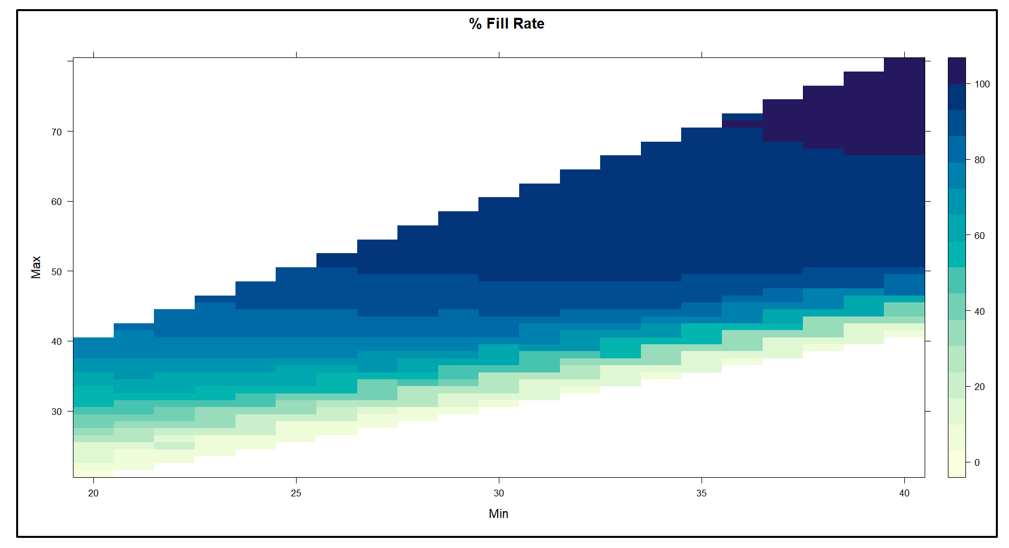
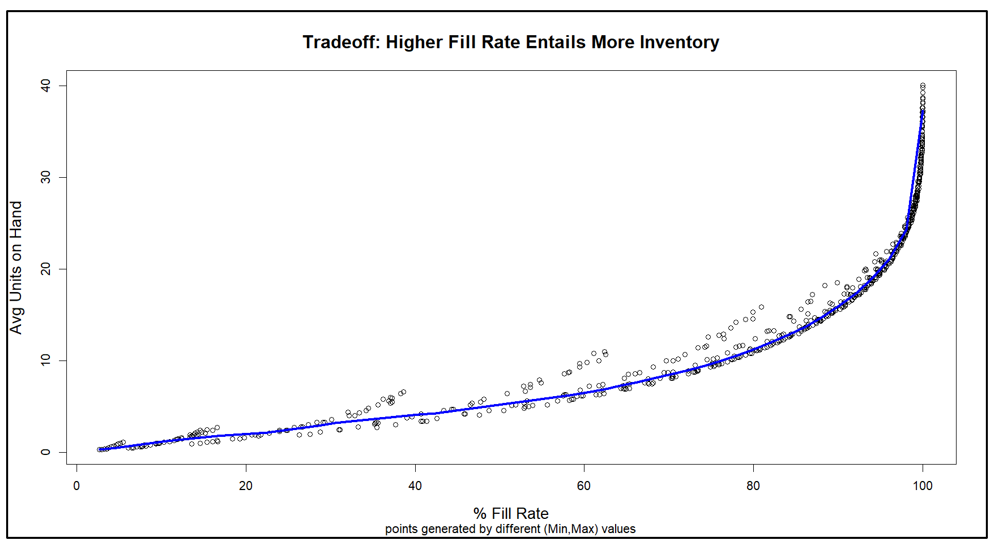
Het Amerikaanse leger heeft een gezegde: “Tijd besteed aan verkenning is nooit verspilde tijd.” Zo nu en dan, onze Slimme voorspeller blog heeft een bericht waarmee je je hoofd op een draai kunt zetten om te zien wat er om je heen gebeurt. Een voorbeeld is ons bericht op digitale tweelingen, een hot topic in de technische wereld. Samenvattend: het gebruik van vraag- en aanbodsimulaties om zwakke punten in uw voorraadplan op te sporen is een vorm van supply chain-verkenning. Door deze gaten in het toezicht te dichten, kunnen bedrijven corrigerende maatregelen nemen voordat zich een daadwerkelijk probleem voordoet.

Situationele bewustzijnsverschillen

Een militaire commandant moet bijhouden wat er beschikbaar is voor gebruik en hoe goed het wordt gebruikt. De rapporten beschikbaar in Smart Operational Analytics houdt u op de hoogte van uw voorraadaantallen, de nauwkeurigheid van uw prognoses, het reactievermogen van uw leveranciers en trends op deze en andere operationele gebieden. U weet precies waar u staat op het gebied van diverse supply chain-KPI's, zoals serviceniveau, opvullingspercentages en voorraadomloop. U weet of de werkelijke prestaties overeenkomen met de geplande prestaties en of het voorraadplan (dat wil zeggen wat u moet bestellen, wanneer, bij wie en waarom) wordt nageleefd of genegeerd.

Behendigheidsverschillen

De zakelijke omgeving kan snel veranderen. Het enige dat nodig is, is een tanker die zijdelings vastzit in het Suezkanaal, een paar ballistische anti-scheepsraketten in de Rode Zee, of een weersgebeurtenis in de hele regio. Deze catastrofes kunnen net zo goed op de hoofden van uw concurrenten terechtkomen als op die van u, maar wie van u is wendbaar genoeg om als eerste te reageren? Uitzonderingsrapportage in Vraagplanner en slimme operationele analyses kan grote veranderingen in de aard van de vraag detecteren, zodat u snel verouderde vraaggegevens eruit kunt filteren voordat deze al uw berekeningen voor vraagprognoses of voorraadoptimalisatie vergiftigen. Smart Demand Planner kan vooraf waarschuwen voor een aanstaande stijging of daling van de vraag. Smart Inventory Optimization kan u helpen uw tactieken voor het aanvullen van uw voorraad aan te passen aan deze verschuivingen in de vraag.

Innovatiehiaten

Of je nu naar je concurrentie verwijst als ‘The Other Guys’ of ‘Everybody Else’ of iets dat niet kan worden afgedrukt, degenen waar je je zorgen over moet maken, zijn degenen die altijd op zoek zijn naar een voorsprong. Wanneer u Smart als uw partner kiest, geven wij u die voorsprong met innovatieve maar in de praktijk bewezen voorspellende oplossingen. Smart Software innoveert al sinds de geboorte, meer dan 40 jaar geleden, voorspellende modellen.

• Onze eerste producten introduceerden meerdere technische innovaties: beoordeling van de voorspelde kwaliteit door naar de toekomst te kijken en niet naar het verleden; automatische selectie van de beste uit een reeks concurrerende methodologieën, waarbij gebruik wordt gemaakt van de graphics op de eerste pc's om eenvoudige beheeroverschrijvingen van statistische voorspellingen mogelijk te maken.

• Later hebben we een radicaal andere benadering bedacht en gepatenteerd voor het voorspellen van de intermitterende vraag die kenmerkend is voor zowel reserveonderdelen als dure duurzame goederen. Onze technologie is gepatenteerd en heeft meerdere prijzen ontvangen voor de dramatische verbetering van het voorraadbeheer. De oplossing is nu een in de praktijk bewezen aanpak die wordt gebruikt door veel toonaangevende bedrijven op het gebied van serviceonderdelen, MRO, aftermarket-onderdelen en buitendienst.

• Meer recentelijk neemt het cloudplatform van Smart voor vraagvoorspelling, voorspellende modellering, voorraadoptimalisatie en analyse alle relevante gegevens die anders opgesloten zitten in uw ERP- of EAM-systemen, externe bestanden en andere ongelijksoortige gegevensbronnen, en organiseert deze in de Slimme datapijplijn, structureert het in onze gemeenschappelijk datamodel, en verwerkt deze in onze AWS-wolk. Smart maakt gebruik van de kracht van ons gepatenteerd probabilistische vraagsimulaties in Smart Inventory Optimization om de regels die u gebruikt om elk van uw voorraaditems te beheren, te stresstesten en te optimaliseren.

Het is mijn taak, samen met mijn medeoprichter Dr. Nelson Hartunian, ons data science-team en academische consultants, om de grenzen van supply chain-analyses te blijven verleggen en de voordelen voor u terug te brengen door voortdurend nieuwe versies van onze producten uit te rollen, zodat u zorg ervoor dat u niet blijft steken in een innovatiekloof – of in een van de andere.

Onze klanten hebben doorgaans gekozen voor één manier om hun voorraad serviceonderdelen te beheren. De professor in mij zou graag willen denken dat het gekozen voorraadbeleid een beredeneerde keuze was uit de weloverwogen alternatieven, maar het is waarschijnlijker dat het gewoon zo is gebeurd. Misschien had de inventarishoncho van lang geleden een favoriet en bleef die keuze hangen. Misschien gebruikte iemand een EAM- of ERP-systeem dat maar één keuze bood. Misschien zijn er enkele gissingen gedaan, gebaseerd op de toenmalige omstandigheden.

De concurrenten

Het komt maar zelden voor dat bedrijven deze keuzes op lukrake manieren maken. Maar met moderne planningssoftware voor serviceonderdelen kunt u systematischer uw keuzes maken. Dit bericht demonstreert deze stelling door objectieve vergelijkingen te maken tussen drie populaire voorraadbeleidslijnen: Bestel tot aan, Bestelpunt/Bestelhoeveelheid en Min/Max. Ik heb elk van deze beleidsmaatregelen hierin besproken videoblog.

• Bestel tot. Dit is een periodiek beoordelingsbeleid waarbij elke T dagen de voorhanden voorraad wordt opgeteld en een bestelling van willekeurige grootte wordt geplaatst om het voorraadniveau weer op S-eenheden te brengen.
• Q, R of bestelpunt/bestelhoeveelheid. Q, R is een continu beoordelingsbeleid waarbij de voorraad elke dag wordt opgeteld. Als er Q of minder eenheden beschikbaar zijn, wordt een bestelling van vaste grootte geplaatst voor R meer eenheden.
• Min, Max is een ander continu beoordelingsbeleid waarbij de inventaris elke dag wordt opgeteld. Als er Min of minder eenheden beschikbaar zijn, wordt er een bestelling geplaatst om het voorraadniveau weer op Max eenheden te brengen.

Volgens de inventaristheorie worden deze keuzes gerangschikt in oplopende volgorde van effectiviteit. De eerste optie, Order Up To, is duidelijk de eenvoudigste en goedkoopste om te implementeren, maar sluit de ogen voor wat er gedurende langere tijd gebeurt. Het opleggen van een bepaald tijdsverloop tussen bestellingen maakt het in theorie minder flexibel. De twee continue beoordelingsopties houden daarentegen voortdurend in de gaten wat er gebeurt, zodat ze sneller kunnen reageren op mogelijke voorraadtekorten. De Min/Max-optie is in theorie flexibeler dan de optie die gebruikmaakt van een vast bestelaantal, omdat de omvang van de bestelling dynamisch verandert om aan de vraag te voldoen.

Dat is de theorie. Dit artikel onderzoekt bewijsmateriaal uit onderlinge vergelijkingen om de theorie te controleren en concrete cijfers te geven over de relatieve prestaties van de drie beleidsmaatregelen.

De betekenis van “Beste”

Hoe moeten we de score bijhouden in dit toernooi? Als u een regelmatige lezer bent van dit Smart Forecaster-blog, weet u dat de kern van voorraadplanning een touwtrekken is tussen twee tegengestelde doelstellingen: de voorraad beperkt houden versus de beschikbaarheidsstatistieken van artikelen, zoals het serviceniveau, hoog houden.

Om de zaken te vereenvoudigen, zullen we ‘één getal berekenen dat alles regelt’: de gemiddelde bedrijfskosten. Het winnende beleid zal het beleid zijn met het laagste gemiddelde.

Dit gemiddelde is de som van drie componenten: de kosten van het aanhouden van voorraad (“voorraadkosten”), de kosten van het bestellen van aanvullingseenheden (“bestelkosten”) en de kosten van het mislopen van een verkoop (“tekortkosten”). Om het concreet te maken zijn we uitgegaan van de volgende aannames:

• Elk serviceonderdeel heeft een waarde van $1.000.
• De jaarlijkse bewaarkosten bedragen 10% van de artikelwaarde, of $100 per jaar per eenheid.
• Het verwerken van elke aanvulorder kost $20 per bestelling.
• Elke gevraagde maar niet geleverde eenheid kost de waarde van het onderdeel, $1.000.

Voor de eenvoud zullen we naar de gemiddelde bedrijfskosten verwijzen als eenvoudigweg “de kosten”.

Uiteraard kunnen de laagste gemiddelde kosten worden bereikt door uit het bedrijf te stappen. De concurrentie vereiste dus een prestatiebeperking op het gebied van de beschikbaarheid van artikelen: elke optie moest een opvullingspercentage van minimaal 99% behalen.

De alternatieven: laat het achterwege

Een belangrijk contextelement is of stockouts resulteren in verliezen of nabestellingen. Ervan uitgaande dat het betreffende serviceonderdeel cruciaal is, zijn we ervan uitgegaan dat niet-uitgevoerde bestellingen verloren gaan, wat betekent dat een concurrent de bestelling vervult. In een MRO-omgeving betekent dit extra downtime als gevolg van voorraadtekorten.

Om de alternatieven te vergelijken, hebben we onze voorspellende modelleringsengine gebruikt om er een groot aantal uit te voeren Monte Carlo-simulaties. Elke simulatie omvatte het specificeren van de parameterwaarden van elk beleid (bijvoorbeeld de Min- en Max-waarden), het genereren van een vraagscenario, het invoeren daarvan in de logica van het beleid en het meten van de resulterende kosten, gemiddeld over 365 dagen gebruik. Door dit proces 1000 keer te herhalen en het gemiddelde te nemen van de 1000 resulterende kosten, ontstond het eindresultaat voor elke polis.  

Om de vergelijking eerlijk te maken, moest elk alternatief worden ontworpen voor de beste prestaties. Daarom doorzochten we de ‘ontwerpruimte’ van elke polis om het ontwerp met de laagste kosten te vinden. Dit vereiste het herhalen van het proces dat in de vorige paragraaf is beschreven voor veel paren parameterwaarden en het identificeren van het paar dat de verloren gemiddelde jaarlijkse bedrijfskosten opleverde.

Met behulp van de algoritmen in Smart Inventory Optimization (SIO^TM) hebben we onderlinge vergelijkingen gemaakt op basis van de volgende aannames over vraag en aanbod:

• Er werd aangenomen dat de vraag naar artikelen intermitterend en zeer variabel was, maar relatief eenvoudig omdat er geen sprake was van trends of seizoensinvloeden, zoals vaak het geval is voor serviceonderdelen. De dagelijkse gemiddelde vraag bedroeg 5 eenheden met een grote standaardafwijking van 13 eenheden. Figuur 1 toont een voorbeeld van de vraag over een jaar. We hebben gekozen voor een zeer uitdagend vraagpatroon, waarbij op sommige dagen de vraag 10 tot zelfs 20 keer zo groot is als de gemiddelde vraag.

Figuur 1: Er werd aangenomen dat de dagelijkse vraag naar onderdelen intermitterend en zeer piekerig was.

​​

• De levertijden van leveranciers bedroegen destijds 14 dagen (75%) en anders 21 dagen. Dit weerspiegelt het feit dat er altijd onzekerheid bestaat in de toeleveringsketen.

En de winnaar is…

Klopte de theorie? Soort van'.

Tabel 1 toont de resultaten van de simulatie-experimenten. Voor elk van de drie concurrerende beleidsmaatregelen worden de gemiddelde jaarlijkse bedrijfskosten, de foutmarge (technisch gezien een betrouwbaarheidsinterval van ongeveer 95% voor de gemiddelde kosten) en de ogenschijnlijk beste keuzes voor parameterwaarden weergegeven.

Tabel 1: Resultaten van de gesimuleerde vergelijkingen

De gemiddelde kosten voor de (T,S)-polis wanneer T op 30 dagen is vastgesteld, bedroegen bijvoorbeeld $41.680. Maar de Plus/Minus houdt in dat de resultaten verenigbaar zijn met de “echte” kosten (dwz de schatting op basis van een oneindig aantal simulaties) van ergens tussen $39.890 en $43.650. De reden dat er zoveel statistische onzekerheid is, is de extreem piekerige aard van de vraag in dit voorbeeld.

Tabel 1 laat zien dat in dit voorbeeld de drie beleidsmaatregelen in lijn zijn met de verwachtingen. Nuttigere conclusies zouden echter zijn:

1. Wat de gemiddelde kosten betreft, zijn de drie polissen opmerkelijk vergelijkbaar. Door een slimme keuze van parameterwaarden kan men goede resultaten behalen met elk van de drie beleidsmaatregelen.
2. Niet weergegeven in Tabel 1, maar duidelijk uit de gedetailleerde simulatieresultaten, is dat slechte keuzes voor parameterwaarden rampzalig kunnen zijn voor elk beleid.
3. Het is vermeldenswaard dat het beleid voor periodieke beoordeling (T,S) niet mocht optimaliseren ten opzichte van mogelijke waarden van T. We hebben T op 30 vastgesteld om na te bootsen wat in de praktijk gebruikelijk is, maar degenen die het beleid voor periodieke beoordeling gebruiken, moeten andere beoordelingen overwegen. periodes. Een aanvullend experiment stelde de beoordelingsperiode vast op T = 7 dagen. De gemiddelde kosten in dit scenario werden geminimaliseerd op $36.551 ± $1.668 met S = 343. Dit resultaat is beter dan dat met T = 30 dagen.
4. We moeten voorzichtig zijn met het overgeneraliseren van deze resultaten. Ze zijn afhankelijk van de veronderstelde waarden van de drie kostenparameters (vasthouden, bestellen en tekort) en het karakter van het vraagproces.
5. Het is mogelijk om experimenten zoals hier weergegeven automatisch uit te voeren Smart Inventory Optimization. Dit betekent dat ook jij ontwerpkeuzes op een rigoureuze manier kunt onderzoeken.

Degenen onder u die actuele onderwerpen volgen, zullen bekend zijn met de term ‘digitale tweeling’. Degenen die het te druk hebben gehad met hun werk, willen misschien verder lezen en bijpraten.

Wat is een digitale tweeling?

Hoewel er verschillende definities van digital twin zijn, is er een die goed werkt:

Een digitale tweeling is een dynamiek virtuele kopie van een fysiek bezit, proces, systeem of omgeving die er hetzelfde uitziet en zich identiek gedraagt als zijn tegenhanger in de echte wereld. Een digitale tweeling neemt gegevens op en repliceert processen dus dat kan mogelijke prestatieresultaten voorspellen en problemen die het echte product zou kunnen ondergaan. [Bron: Unity.com]. Voor meer achtergrondinformatie kunt u terecht op Mckinsey.com.

Wat is het verschil tussen een digital twin (hierna DT) en een model? In de eerste plaats wordt een ODC verbonden met realtime gegevens om het model te behouden als een actuele weergave van het systeem waarmee u werkt.

Onze huidige producten zouden we “slow-motion DT's” kunnen noemen, omdat ze meestal worden gebruikt met niet-realtime gegevens (maar geen verouderde gegevens, omdat deze van de ene op de andere dag worden bijgewerkt) en worden toegepast op problemen zoals het plannen van de grondstoffenaankopen voor het volgende kwartaal of het instellen van voorraadparameters voor een maand of langer.

Gebruiken mensen digital twins in mijn branche?

Mijn indruk is dat de penetratie van DT's wellicht het hoogst is in de lucht- en ruimtevaart- en nucleaire industrie. De meeste van onze klanten bevinden zich elders: in de productie, distributie en openbare voorzieningen zoals transport en energie. Binnenkort zullen we nieuwe producten aanbieden die dichter bij de strikte definitie van een DT komen die nauw verbonden is met het systeem dat hij vertegenwoordigt.

DT-voorbeeld

De meeste gebruikers van Smart Inventory Optimization™ (SIO) voer de applicatie periodiek uit, meestal maandelijks. SIO analyseert de huidige vraag naar voorraadartikelen en recente doorlooptijden van leveranciers en zet deze om in respectievelijk vraag- en aanbodscenario's. Vervolgens stellen gebruikers interactief (voor individuele artikelen) of automatisch (op schaal) parameters voor voorraadbeheer in die de gewenste gemiddelde prestaties op lange termijn opleveren, waarbij de concurrerende doelen van het minimaliseren van de voorraad in evenwicht worden gebracht en tegelijkertijd een voldoende niveau van artikelbeschikbaarheid wordt gegarandeerd.

Smart Supply Planner (SSP) reageert op een directere manier op onvoorziene gebeurtenissen. Elke dag kan er een abnormale bestelling plaatsvinden die de vraag doet toenemen, bijvoorbeeld wanneer een nieuwe klant een verrassende eerste voorraadbestelling plaatst. Of een belangrijke leverancier kan een probleem ervaren in zijn fabriek en gedwongen worden de verzending van uw geplande aanvullingsorders uit te stellen. Op de lange termijn worden deze onvoorziene omstandigheden gemiddeld en rechtvaardigen ze de aanbevelingen die uit SIO komen. SSP biedt u echter een manier om op de korte termijn te reageren en kansen te grijpen of kogels te ontwijken.

In de kern werkt SSP als SIO, in die zin dat het scenariogestuurd is. De verschillen zijn dat het korte planningshorizon gebruikt en real-time initiële omstandigheden gebruikt als basis voor zijn simulaties van de prestaties van voorraadsystemen. Vervolgens zal het realtime aanbevelingen doen voor interventies die de verstoring veroorzaakt door de onvoorziene gebeurtenissen compenseren. Dit omvat onder meer het annuleren of versnellen van aanvullingsorders.

Overzicht

Met Digital Twins kunt u plannen ‘in silico’ uitproberen voordat u ze in de fabriek of het magazijn implementeert. De kern bestaat uit wiskundige modellen van uw bedrijfsvoering, maar verbonden met realtime gegevens. Ze bieden een ‘digitale sandbox’ waarin u ideeën kunt uitproberen en direct voorspellingen kunt krijgen over hoe goed ze zullen werken. Veel meer dan een spreadsheet zullen DT's binnenkort het belangrijkste hulpmiddel zijn in uw gereedschapskist voor voorraadplanning.

Sommige bedrijven investeren in software om hen te helpen hun voorraad te beheren, of het nu gaat om reserveonderdelen of eindproducten. Maar een verrassend aantal anderen speelt elke dag het Inventory Guessing Game, vertrouwend op een ingebeelde “Golden Gut” of op gewoon geluk om hun inventariscontroleparameters in te stellen. Maar wat voor resultaten verwacht je met die aanpak?

Hoe goed bent u in het aanvoelen van de juiste waarden? In deze blogpost wordt u uitgedaagd om de beste Min- en Max-waarden voor een notioneel voorraaditem te raden. We laten u de vraaggeschiedenis zien, geven u een paar relevante feiten, waarna u Min- en Max-waarden kunt kiezen en zien hoe goed ze zouden werken. Klaar?

De uitdaging

Figuur 1 toont de dagelijkse vraaggeschiedenis van het artikel. De gemiddelde vraag bedraagt 2 eenheden per dag. De doorlooptijd voor het aanvullen is constant 10 dagen (wat onrealistisch is maar in uw voordeel werkt). Bestellingen die niet direct uit voorraad leverbaar zijn, kunnen niet worden nabesteld en gaan verloren. U wilt minimaal een opvullingspercentage van 80% bereiken, maar niet tegen elke prijs. U wilt ook het gemiddelde aantal beschikbare eenheden minimaliseren en toch een opvullingspercentage van ten minste 80% bereiken. Welke Min- en Max-waarden zouden een 80%-opvullingspercentage opleveren met het laagste gemiddelde aantal beschikbare eenheden? [Neem uw antwoorden op, zodat u ze later kunt controleren. De oplossing staat hieronder aan het einde van het artikel.]

Berekening van de beste min- en max-waarden

De manier om de beste waarden te bepalen is door een digitale tweeling te gebruiken, ook wel een Monte Carlo-simulatie genoemd. De analyse creëert een groot aantal vraagscenario's en passeert deze door de wiskundige logica van het voorraadbeheersysteem om te zien welke waarden zullen worden overgenomen door de belangrijkste prestatie-indicatoren (KPI's).

We hebben voor dit probleem een digitale tweeling gebouwd en deze systematisch getest met 1.085 paar Min- en Max-waarden. Voor elk paar hebben we in totaal 100 keer 365 bedrijfsdagen gesimuleerd. Vervolgens hebben we het gemiddelde van de resultaten genomen om de prestaties van het Min/Max-paar te beoordelen in termen van twee KPI's: opvullingspercentage en gemiddelde voorraad.

Figuur 2 toont de resultaten. De inherente afweging tussen voorraadomvang en opvullingspercentage is duidelijk in de figuur: als je een hoger opvullingspercentage wilt, moet je een grotere voorraad accepteren. Op elk inventarisniveau is er echter een bereik aan opvullingspercentages, dus het is de bedoeling om het Min/Max-paar te vinden dat het hoogste opvullingspercentage oplevert voor een inventaris van een bepaalde grootte.

Een andere manier om Figuur 2 te interpreteren is door te focussen op de groene stippellijn die het beoogde 80%-opvullingspercentage aangeeft. Er zijn veel Min/Max-paren die in de buurt van het 80%-doel kunnen raken, maar ze verschillen qua voorraadgrootte van ongeveer 6 tot ongeveer 8 eenheden. Figuur 3 zoomt in op dat gebied van Figuur 2 en toont een behoorlijk aantal Min/Max-paren die competitief zijn.

We hebben de resultaten van alle 1.085 simulaties gesorteerd om te identificeren wat economen de efficiënte grens noemen. De efficiënte grens is de reeks meest efficiënte Min/Max-paren om de wisselwerking tussen opvullingspercentage en aanwezige eenheden te benutten. Dat wil zeggen, het is een lijst met Min/Max-paren die de goedkoopste manier bieden om elk gewenst opvullingspercentage te bereiken, niet alleen 80%. Figuur 4 toont de efficiënte grens voor dit probleem. Van links naar rechts kunt u de laagste prijs aflezen die u zou moeten betalen (gemeten aan de hand van de gemiddelde voorraadgrootte) om het beoogde opvullingspercentage te bereiken. Om bijvoorbeeld een opvullingspercentage van 90% te bereiken, zou u een gemiddelde voorraad van ongeveer 10 eenheden moeten hebben.

Figuren 2, 3 en 4 tonen resultaten voor verschillende Min/Max-paren, maar geven niet de waarden van Min en Max achter elk punt weer. Tabel 1 toont alle simulatiegegevens: de waarden van Min, Max, gemiddelde beschikbare eenheden en opvullingspercentage. Het antwoord op het raadspel is gemarkeerd in de eerste regel van de tabel: Min=7 en Max=13¹. Heb je het juiste antwoord gekregen, of iets dat in de buurt komt?²? Heb je misschien de efficiënte grens bereikt?

Conclusies

Misschien heb je geluk gehad, of misschien heb je inderdaad een Gouden Darm, maar de kans is groter dat je niet het juiste antwoord hebt gekregen, en nog waarschijnlijker dat je het niet eens hebt geprobeerd. Het vinden van het juiste antwoord is buitengewoon moeilijk zonder de digitale tweeling te gebruiken. Raden is onprofessioneel.

Een stap verder dan raden is ‘raden en zien’, waarbij u uw gok implementeert en vervolgens een tijdje (maanden?) wacht om te zien of de resultaten u bevallen. Die tactiek is op zijn minst ‘wetenschappelijk’, maar inefficiënt.

Denk nu eens aan de moeite om de beste (Min,Max) paren voor duizenden items te bepalen. Op die schaal is er zelfs nog minder reden om het inventarisraadspel te spelen. Het juiste antwoord is om het te spelen… Slim³.

¹ Dit antwoord heeft een bonus, omdat het een opvullingspercentage van iets meer dan 80% behaalt bij een lagere gemiddelde voorraadgrootte dan de Min/Max-combinatie die precies 80% bereikte. Met andere woorden: (7,13) bevindt zich op de efficiënte grens.

² Omdat deze resultaten afkomstig zijn van een simulatie in plaats van een exacte wiskundige vergelijking, is er een bepaalde foutmarge verbonden aan elk geschat opvullingspercentage en voorraadniveau. Omdat de gemiddelde resultaten echter gebaseerd waren op 100 simulaties over een periode van 365 dagen, zijn de foutmarges echter klein. Over alle experimenten heen waren de gemiddelde standaardfouten in het opvullingspercentage en de gemiddelde voorraad respectievelijk slechts 0,009% en 0,129 eenheden.

³ Mocht je dit nog niet weten: een van de oprichters van Smart Software was … Charlie Smart.

Evenwichtsoefening

Bij voorraadbeheer gaat het, net als bij alles, om het balanceren van concurrerende prioriteiten. Wilt u een lean inventaris? Ja! Wil jij kunnen zeggen “Het is op voorraad” als een klant iets wil kopen? Ja!

Maar kun je het op beide manieren hebben? Slechts tot op zekere hoogte. Als u uw voorraad te agressief aanpast, riskeert u voorraadtekorten. Als je voorraadtekorten uitroeit, creëer je een opgeblazen voorraad. U wordt gedwongen een bevredigend evenwicht te vinden tussen de twee concurrerende doelen: een beperkte voorraad en een hoge beschikbaarheid van artikelen.

Een balans bereiken

Hoe breng je dat evenwicht tot stand? Te veel voorraadplanners 'schatten' hun weg naar een of ander antwoord. Of ze bedenken een keer een slim antwoord en hopen dat het een verre houdbaarheidsdatum heeft en blijven het gebruiken terwijl ze zich op andere problemen concentreren. Helaas zullen verschuivingen in de vraag en/of veranderingen in de prestaties van leveranciers en/of verschuivingen in de prioriteiten van uw eigen bedrijf oude voorraadplannen overbodig maken en u weer terugbrengen waar u begon.

Het is onvermijdelijk dat elk plan een houdbaarheidsdatum heeft en moet worden bijgewerkt. Het is echter zeker niet de beste praktijk om de ene gok door de andere te vervangen. In plaats daarvan zou elke planningscyclus gebruik moeten maken van moderne supply chain-software om giswerk te vervangen door op feiten gebaseerde analyses met behulp van waarschijnlijkheidsberekeningen.

Ken jezelf

Het enige dat software niet kan, is een beste antwoord berekenen zonder uw prioriteiten te kennen. Hoeveel prioriteit geeft u aan lean inventory boven artikelbeschikbaarheid? Software voorspelt de voorraad- en beschikbaarheidsniveaus die worden veroorzaakt door de beslissingen die u neemt over het beheer van elk item in uw inventaris, maar alleen u kunt beslissen of een bepaalde reeks belangrijke prestatie-indicatoren consistent is met wat u wilt.

Weten wat je wilt in algemene zin is gemakkelijk: je wilt alles. Maar weten wat je voorkeur heeft bij het vergelijken van specifieke scenario's is moeilijker. Het helpt om een scala aan realiseerbare mogelijkheden te kunnen zien en na te denken over wat het beste lijkt als ze naast elkaar worden gelegd.

Zie wat het volgende is

Supply chain-software kan u inzicht geven in de afwegingscurve. Over het algemeen weet u dat een beperkte voorraad en een hoge beschikbaarheid van artikelen elkaar tegenwerken, maar het zien van artikelspecifieke afwegingscurven verscherpt uw focus.

Waarom is er een bocht? Omdat u keuzes heeft over hoe u elk item beheert. Als u bijvoorbeeld voortdurend de voorraadstatus controleert, welke waarden wijst u dan toe aan de Min en Max waarden die bepalen wanneer aanvullingen moeten worden besteld en hoeveel er moet worden besteld. De afwegingscurve ontstaat omdat het kiezen van verschillende Min- en Max-waarden leidt tot verschillende niveaus van bij de hand inventaris en verschillende niveaus van artikelbeschikbaarheid, bijvoorbeeld zoals gemeten door vulpercentage.

Een scenario voor analyse

Om deze ideeën te illustreren, gebruikte ik a digitale tweeling  om in te schatten hoe verschillende waarden van Min en Max in een bepaald scenario zouden presteren. Het scenario concentreerde zich op een fictief reserveonderdeel met een puur willekeurige vraag met een redelijk hoog niveau onderbreking (37% aan dagen zonder vraag). De doorlooptijden voor het aanvullen waren een fluitje van een cent tussen 7 en 14 dagen. De Min- en Max-waarden werden systematisch gevarieerd: Min van 20 tot 40 eenheden, Max van Min+1 eenheden tot 2xMin eenheden. Elk (Min,Max) paar werd in totaal 1000 keer gesimuleerd gedurende 365 dagen gebruik. Vervolgens werden de resultaten gemiddeld om zowel het gemiddelde aantal beschikbare eenheden als het vulpercentage te schatten, dat wil zeggen het percentage van de dagelijkse behoeften waaraan onmiddellijk werd voldaan vanaf voorraad. Als de voorraad niet beschikbaar was, werd deze nabesteld.

Resultaten

Het experiment leverde twee soorten resultaten op:

• Grafieken die de relatie tonen tussen de min- en max-waarden en twee belangrijke prestatie-indicatoren: opvullingspercentage en gemiddelde beschikbare eenheden.
• Een afwegingscurve die laat zien hoe het opvullingspercentage en de beschikbare eenheden met elkaar in evenwicht zijn.

Figuur 1 toont de beschikbare inventaris als functie van de waarden van Min en Max. Het experiment leverde handniveaus op variërend van bijna 0 tot ongeveer 40 eenheden. Over het algemeen resulteert het constant houden van Min en het verhogen van Max in meer beschikbare eenheden. De relatie met Min is complexer: Max constant houden, Min verhogen voegt eerst de voorraad toe, maar vermindert deze op een gegeven moment.

Figuur 2 toont het vulpercentage als functie van de waarden Min en Max. Het experiment leverde opvullingspercentages op variërend van bijna 0% tot 100%. Over het algemeen weerspiegelden de functionele relaties tussen het opvullingspercentage en de waarden van Min en Max die in Figuur 1.

Figuur 3 maakt het belangrijkste punt duidelijk en laat zien hoe het variëren van Min en Max tot een perverse combinatie van de belangrijkste prestatie-indicatoren leidt. Over het algemeen zijn de waarden Min en Max die de beschikbaarheid van artikelen maximaliseren (opvullingspercentage) dezelfde waarden die de voorraadkosten maximaliseren (gemiddelde beschikbare eenheden). Dit algemene patroon wordt weergegeven door de blauwe curve. De experimenten leverden ook enkele uitlopers van de blauwe curve op die verband houden met slechte keuzes voor Min en Max, in de zin dat andere keuzes deze domineren door hetzelfde opvullingspercentage te produceren met een lagere voorraad.

Conclusies

Figuur 3 maakt duidelijk dat uw keuze voor het beheer van een voorraadartikel u dwingt om voorraadkosten af te wegen tegen de beschikbaarheid van artikelen. Je kunt enkele inefficiënte combinaties van Min- en Max-waarden vermijden, maar je kunt niet aan de afweging ontsnappen.

De goede kant van deze realiteit is dat je niet hoeft te raden wat er zal gebeuren als je je huidige waarden van Min en Max naar iets anders verandert. De software vertelt u wat de verhuizing u oplevert en wat het u gaat kosten. U kunt uw Guestimator-hoed afzetten en met vertrouwen uw ding doen.

Figuur 1 Voorhanden inventaris als functie van de min- en max-waarden

Figuur 2 Vulsnelheid als functie van Min- en Max-waarden

Figuur 3 Afwegingscurve tussen opvullingspercentage en voorhanden voorraad