Misschien herinner je je het verhaal van Goudlokje uit je jeugd lang geleden. Soms was de pap te heet, soms te koud, maar een keer was het precies goed. Nu we volwassen zijn, kunnen we dat sprookje vertalen in een professioneel principe voor voorraadplanning: er kan te weinig of te veel voorraad zijn en er is een bepaald Goudlokje-niveau dat "precies goed" is. Deze blog gaat over het vinden van die sweet spot.

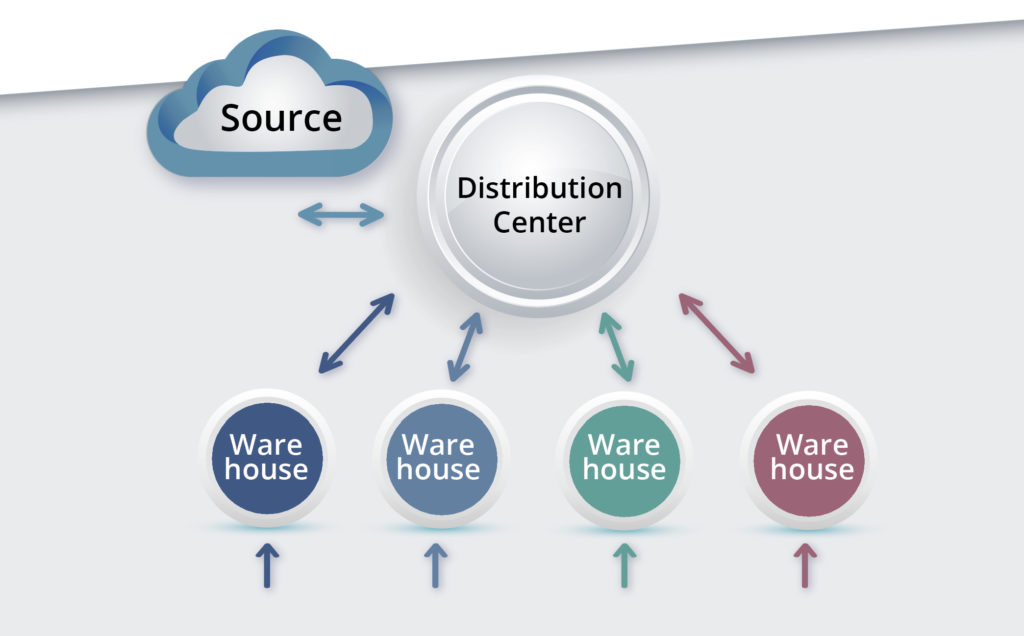
Bekijk dit voorbeeld om onze fabel over de toeleveringsketen te illustreren. Stelt u zich eens voor dat u serviceonderdelen verkoopt om de systemen van uw klanten draaiende te houden. U biedt een bepaald serviceonderdeel aan dat u $100 kost om te maken, maar dat wordt verkocht voor een opslag van 20%. Je kunt $20 verdienen met elke eenheid die je verkoopt, maar je mag niet de hele $20 houden vanwege de voorraadkosten die je draagt om het onderdeel te kunnen verkopen. Er zijn onderhoudskosten om het onderdeel in goede staat te houden terwijl het op voorraad is en bestelkosten om eenheden die u verkoopt aan te vullen. Ten slotte verliest u soms inkomsten uit verloren verkopen als gevolg van stockouts.  

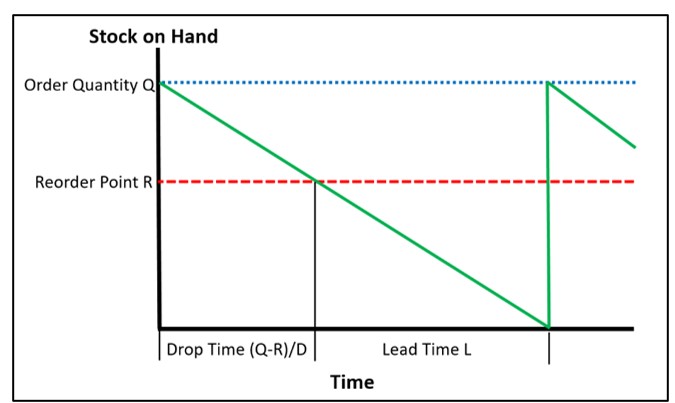
Deze bedrijfskosten kunnen rechtstreeks verband houden met de manier waarop u het onderdeel in voorraad beheert. Neem voor ons voorbeeld aan dat u een (Q,R) voorraadbeleid gebruikt, waarbij Q de hoeveelheid voor de aanvullingsorder is en R het bestelpunt is. Neem verder aan dat de reden dat u geen $30 per eenheid maakt, is dat u concurrenten heeft en dat klanten het onderdeel van hen zullen krijgen als ze het niet van u kunnen krijgen.

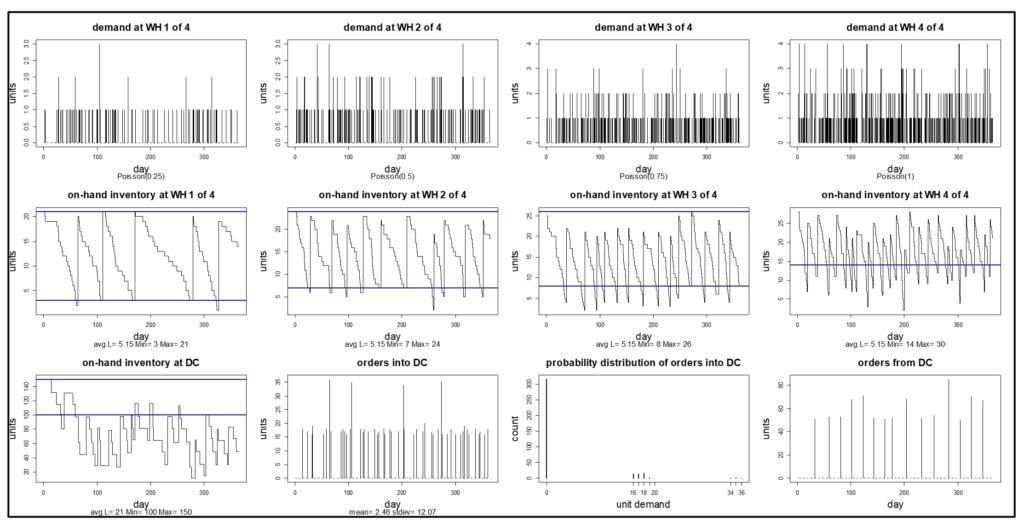
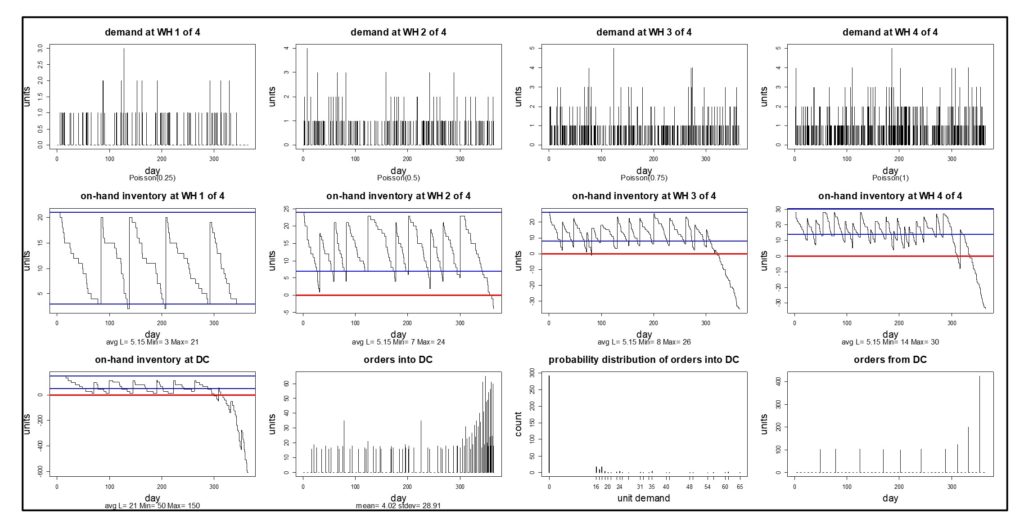
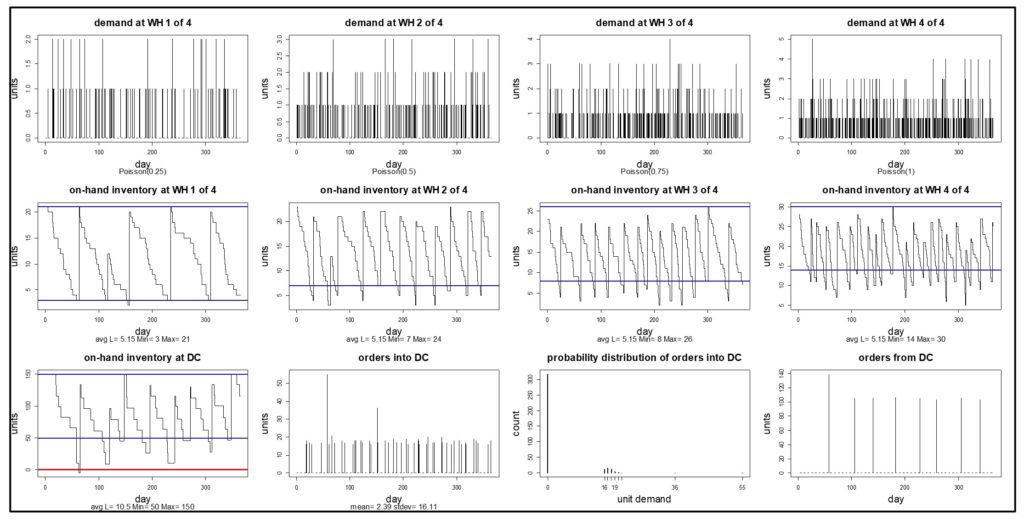
Zowel uw omzet als uw kosten zijn op complexe manieren afhankelijk van uw keuzes voor Q en R. Deze zullen bepalen hoeveel u bestelt, wanneer en dus hoe vaak u bestelt, hoe vaak uw voorraad op is en dus hoeveel verkopen u verliest, en hoeveel contant geld dat u vastlegt in de inventaris. Het is onmogelijk om deze relaties op basis van giswerk uit te rekenen, maar moderne software kan de relaties zichtbaar maken en de dollarcijfers berekenen die u nodig hebt om uw keuze van waarden voor Q en R te sturen. Het doet dit door gedetailleerde, op feiten gebaseerde, probabilistische simulaties uit te voeren die kosten en prestaties voorspellen door middel van een groot aantal realistische vraagscenario's.  

Met deze resultaten in de hand, kunt u de marge berekenen die is gekoppeld aan (Q,R) waarden met behulp van de eenvoudige formule

Marge = (Vraag - Verloren omzet) x Winst per verkochte eenheid - Bestelkosten - Aanhoudingskosten.

In deze formule zijn gederfde verkopen, bestelkosten en bewaarkosten afhankelijk van bestelpunt R en bestelhoeveelheid Q.

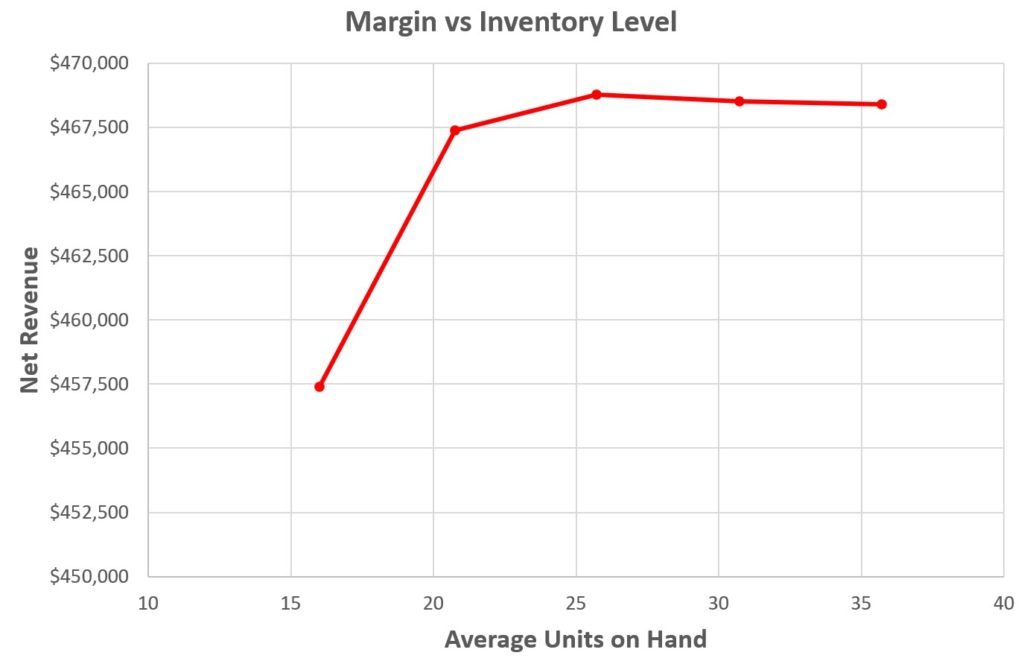
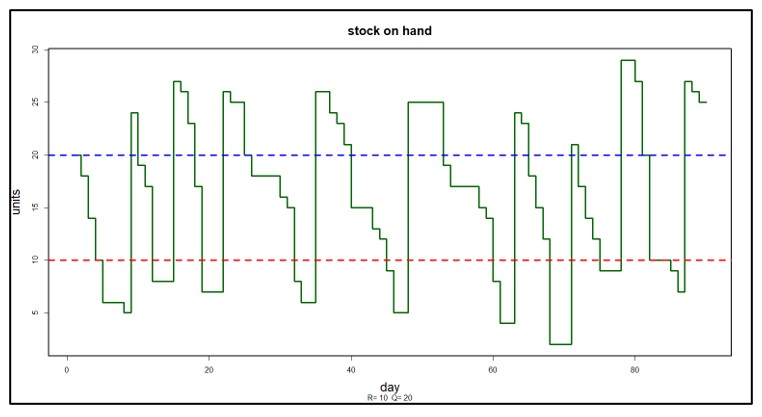
Afbeelding 1 toont het resultaat van simulaties die Q vaststelden op 25 eenheden en R varieerden van 10 tot 30 in stappen van 5. Hoewel de curve bovenaan vrij vlak is, zou u het meeste geld verdienen door een voorraad van ongeveer 25 eenheden aan te houden ( wat overeenkomt met instelling R = 20). Meer voorraad, ondanks een hoger serviceniveau en minder verloren verkopen, zou iets minder geld opleveren (en veel meer geld opleveren), en minder voorraad zou veel minder opleveren.

Figuur 1: Aantonen dat er te weinig of te veel voorraad aanwezig kan zijn

Zonder te vertrouwen op de inventarissimulatiesoftware, zouden we niet kunnen ontdekken:

• a) dat het mogelijk is om te weinig en te veel inventaris te dragen
• b) wat het beste voorraadniveau is?
• c) hoe er te komen door de juiste keuzes van bestelpunt R en bestelhoeveelheid Q.

Zonder een expliciet begrip van het bovenstaande, zullen bedrijven dagelijkse voorraadbeslissingen nemen op basis van onderbuikgevoel en op middeling gebaseerde vuistregels. De hier beschreven afwegingen worden niet blootgelegd en de resulterende mix van voorraad levert een veel lager rendement op, waardoor honderdduizenden tot miljoenen per jaar aan gederfde winst verloren gaan. Dus wees als Goudlokje. Met de juiste systemen en softwaretools kunt u het ook precies goed krijgen!    

Het beheren van de inventaris in een enkele faciliteit is al moeilijk genoeg, maar het probleem wordt veel complexer wanneer er meerdere faciliteiten zijn die in meerdere echelons zijn gerangschikt. De complexiteit komt voort uit de interacties tussen de echelons, waarbij de eisen op de lagere niveaus opborrelen en eventuele tekorten op de hogere niveaus die naar beneden stromen.

Als elk van de faciliteiten afzonderlijk zou worden beheerd, zouden standaardmethoden kunnen worden gebruikt, zonder rekening te houden met interacties, om parameters voor voorraadbeheer in te stellen, zoals bestelpunten en bestelhoeveelheden. Het negeren van de interacties tussen niveaus kan echter leiden tot catastrofale storingen. Ervaring en vallen en opstaan maken het ontwerpen van stabiele systemen mogelijk, maar die stabiliteit kan worden verstoord door veranderingen in vraagpatronen of doorlooptijden of door toevoeging van nieuwe faciliteiten. Het omgaan met dergelijke veranderingen wordt enorm geholpen door geavanceerde supply chain-analyses, die een veilige "sandbox" bieden waarin voorgestelde systeemwijzigingen kunnen worden getest voordat ze worden geïmplementeerd. Deze blog illustreert dat punt.

Het scenario

Om enige hoop te hebben dit probleem op een nuttige manier te bespreken, zal deze blog het probleem vereenvoudigen door de hiërarchie op twee niveaus te beschouwen die is afgebeeld in figuur 1. Stel u voor dat de faciliteiten op het lagere niveau magazijnen (WH's) zijn van waaruit moet worden voldaan aan de eisen van de klant , en dat de inventarisitems bij elke WH serviceonderdelen zijn die aan een breed scala aan externe klanten worden verkocht.

Figuur 1: Algemene structuur van één type voorraadsysteem op twee niveaus

Stel je voor dat het hogere niveau zou bestaan uit één distributiecentrum (DC) dat klanten niet rechtstreeks bedient, maar wel de WH's aanvult. Neem voor de eenvoud aan dat het DC zelf wordt aangevuld vanuit een Bron die altijd voldoende voorraad heeft (of maakt) om onderdelen onmiddellijk naar het DC te verzenden, zij het met enige vertraging. (Als alternatief zouden we het systeem kunnen overwegen om winkels door één magazijn te laten bevoorraden).

Elk niveau kan worden beschreven in termen van vraagniveaus (behandeld als willekeurig), doorlooptijden (willekeurig), voorraadbeheerparameters (hier, Min- en Max-waarden) en tekortbeleid (hier, naleveringen toegestaan).

De analysemethode

De academische literatuur heeft vooruitgang geboekt met betrekking tot dit probleem, hoewel dit meestal ten koste gaat van vereenvoudigingen die nodig zijn om een zuiver wiskundige oplossing mogelijk te maken. Onze aanpak is hier toegankelijker en flexibeler: Monte Carlo simulatie. Dat wil zeggen, we bouwen een computerprogramma dat de logica van de systeemwerking bevat. Het programma "creëert" willekeurige vraag op WH-niveau, verwerkt de vraag volgens de logica van een gekozen voorraadbeleid en creëert vraag naar het DC door de willekeurige verzoeken om aanvulling van de WH's te bundelen. Met deze benadering kunnen we veel gesimuleerde dagen van systeemwerking observeren terwijl we letten op belangrijke gebeurtenissen zoals stockouts op beide niveaus.

Een voorbeeld

Om een analyse te illustreren, hebben we een systeem gesimuleerd dat bestaat uit vier WH's en één DC. De gemiddelde vraag varieerde over de WH's. Aanvulling van het DC naar een WH duurde 4 tot 7 dagen, gemiddeld 5,15 dagen. Het aanvullen van de DC van de Bron duurde 7, 14, 21 of 28 dagen, maar 90% van de tijd was ofwel 21 of 28 dagen, wat neerkomt op een gemiddelde van 21 dagen. Elke faciliteit had Min- en Max-waarden die na enkele ruwe berekeningen werden bepaald door het oordeel van analisten.

Figuur 2 toont de resultaten van een jaar gesimuleerde dagelijkse werking van dit systeem. De eerste rij in de figuur toont de dagelijkse vraag naar het item bij elke WH, waarvan werd aangenomen dat het "puur willekeurig" was, wat betekent dat het een Poisson-verdeling had. De tweede rij toont de voorhanden voorraad aan het einde van elke dag, met Min- en Max-waarden aangegeven door blauwe lijnen. De derde rij beschrijft de operaties op het DC. In tegenstelling tot de veronderstelling van veel theorieën, was de vraag naar het DC niet in de buurt van Poisson, en evenmin was de vraag vanuit het DC naar de Bron. In dit scenario waren de Min- en Max-waarden voldoende om ervoor te zorgen dat de artikelbeschikbaarheid hoog was bij elke WH en bij het DC, en er werden geen stockouts waargenomen bij een van de vijf faciliteiten.

Klik hier om de afbeelding te vergroten

Figuur 2 – Gesimuleerd gebruiksjaar van een systeem met vier WH's en één DC.

Laten we nu het scenario variëren. Wanneer stockouts uiterst zeldzaam zijn, zoals in figuur 2, is er vaak overtollige voorraad in het systeem. Stel dat iemand suggereert dat het voorraadniveau op het DC er een beetje dik uitziet en denkt dat het een goed idee zou zijn om daar geld te besparen. Hun suggestie om de voorraad op het DC te verminderen is om de waarde van de Min op het DC te verlagen van 100 naar 50. Wat gebeurt er? Je zou kunnen raden, of je zou kunnen simuleren.

Figuur 3 toont de simulatie – het resultaat is niet mooi. Het systeem werkt een groot deel van het jaar prima, daarna raakt de voorraad van het DC op en kan het de achterstand niet meer inhalen ondanks het sturen van opeenvolgend grotere aanvullingsorders naar de bron. Drie van de vier WH's komen tegen het einde van het jaar in een doodsspiraal terecht (en WH1 volgt daarna). De simulatie heeft een gevoeligheid aan het licht gebracht die niet kan worden genegeerd en heeft een slechte beslissing gemarkeerd.

Klik hier om de afbeelding te vergroten

Figuur 3 – Gesimuleerde effecten van het verlagen van de Min bij de DC.

Nu kunnen de voorraadbeheerders terug naar de tekentafel en andere mogelijke manieren testen om de investering in voorraad op DC-niveau te verminderen. Een stap die altijd helpt, als u en uw leverancier dit samen kunnen realiseren, is om een flexibeler systeem te creëren door de doorlooptijd voor aanvullingen te verkorten. Door samen te werken met de bron om ervoor te zorgen dat het DC altijd binnen 7 of 14 dagen wordt aangevuld, wordt het systeem gestabiliseerd, zoals weergegeven in afbeelding 4.

Klik hier om de afbeelding te vergroten

Figuur 4 – Gesimuleerde effecten van het verkorten van de doorlooptijd voor het aanvullen van het DC.

Helaas is het voornemen om de voorraad op het DC te verminderen niet gehaald. De oorspronkelijke dagelijkse voorraadtelling was ongeveer 80 eenheden en blijft ongeveer 80 eenheden na verlaging van de DC's Min en drastische verbetering van de Source-to-DC doorlooptijd. Maar met het simulatiemodel kan het planningsteam andere ideeën uitproberen tot ze tot een bevredigend herontwerp komen. Of, aangezien figuur 4 laat zien dat de DC-voorraad met nul begint te flirten, zouden ze het misschien verstandig vinden om de behoefte aan gemiddeld ongeveer 80 eenheden in het DC te accepteren en in plaats daarvan te zoeken naar manieren om de voorraadinvesteringen bij de WH's te verminderen.

De afhaalrestaurants

1. Multiechelon voorraadoptimalisatie (MEIO) is complex. Veel factoren werken samen om systeemgedrag te produceren dat zelfs in eenvoudige systemen met twee niveaus verrassend kan zijn.
2. Monte Carlo-simulatie is een handig hulpmiddel voor planners die nieuwe systemen moeten ontwerpen of bestaande systemen moeten aanpassen.

Voor de meeste kleine tot middelgrote fabrikanten en distributeurs is voorraadoptimalisatie op één niveau of op één echelon het allernieuwste in de logistieke praktijk. Multi-echelon voorraadoptimalisatie (“MEIO”) houdt in dat het spel op een nog hoger niveau wordt gespeeld en is daarom veel minder gebruikelijk. Deze blog is de eerste van twee. Het is bedoeld om uit te leggen wat MEIO is, waarom standaard MEIO-theorieën kapot gaan en hoe probabilistische modellering door scenariosimulatie de realiteit in het MEIO-proces kan herstellen. De tweede blog laat een specifiek voorbeeld zien.

Definitie van voorraadoptimalisatie

Een inventarisatiesysteem is gebaseerd op een reeks ontwerpkeuzes.

De eerste keuze is het beleid om te reageren op stockouts: verlies je gewoon de verkoop aan een concurrent, of kun je de klant overtuigen om een backorder te accepteren? Het eerste komt vaker voor bij distributeurs dan bij fabrikanten, maar dit is misschien niet zo'n goede keuze, omdat klanten het antwoord kunnen dicteren.

De tweede keuze is het voorraadbeleid. Deze zijn onderverdeeld in beleid voor "doorlopende beoordeling" en "periodieke beoordeling", met verschillende opties binnen elk type. U kunt een koppeling maken naar een videozelfstudie waarin verschillende algemene voorraadbeleidsregels worden beschreven hier. Misschien is de meest efficiënte bij beoefenaars bekend als "Min/Max" en bij academici als (s, S) of "kleine S, Grote S." We gebruiken dit beleid in onderstaande scenariosimulaties. Het werkt als volgt: Wanneer de voorhanden voorraad daalt tot of onder de Min (s), wordt een bestelling geplaatst voor aanvulling. De grootte van de bestelling is het gat tussen de voorhanden voorraad en de Max (S), dus als Min 10 is, Max 25 en voorhanden is 8, dan is het tijd voor een bestelling van 25-8 = 17 eenheden.

De derde keuze is om te beslissen over de beste waarden van de 'parameters' van het voorraadbeleid, bijv. de waarden die moeten worden gebruikt voor Min en Max. Voordat u getallen aan Min en Max toewijst, moet u duidelijkheid hebben over wat "beste" voor u betekent. Gewoonlijk betekent beste keuzes die de bedrijfskosten van de voorraad minimaliseren, afhankelijk van een minimum aan artikelbeschikbaarheid, uitgedrukt als Service Level of Fill Rate. In wiskundige termen is dit een "tweedimensionaal beperkt geheeltallig optimalisatieprobleem". "Tweedimensionaal" omdat je twee getallen moet kiezen: Min en Max. "Integer" omdat Min en Max hele getallen moeten zijn. "Beperkt" omdat u minimum- en maximumwaarden moet kiezen die een voldoende hoog niveau van artikelbeschikbaarheid bieden, zoals serviceniveaus en opvulpercentages. “Optimalisatie” omdat je daar wilt komen met de laagste operationele kosten (operationele kosten combineren kosten voor vasthouden, bestellen en tekorten).

Multiechelon-inventarisatiesystemen

Het optimalisatieprobleem wordt moeilijker in multi-echelonsystemen. In een systeem met één echelon kan elk voorraadartikel afzonderlijk worden geanalyseerd: één paar Min/Max-waarden per SKU. Omdat er meer onderdelen zijn in een multi-echelonsysteem, is er een groter rekenprobleem.

Afbeelding 1 toont een eenvoudig systeem met twee niveaus voor het beheren van een enkele SKU. Op het lagere niveau komen de vragen binnen bij meerdere magazijnen. Wanneer die dreigen op te raken, worden ze bevoorraad vanuit een distributiecentrum (DC). Wanneer de DC zelf dreigt vol te raken, wordt deze geleverd door een externe bron, zoals de fabrikant van het artikel.

Het ontwerpprobleem hier is multidimensionaal: we hebben Min- en Max-waarden nodig voor 4 magazijnen en voor het DC, dus de optimalisatie vindt plaats in 4×2+1×2=10 dimensies. De analyse moet rekening houden met een groot aantal contextuele factoren:

• Het gemiddelde niveau en de volatiliteit van de vraag die in elk magazijn binnenkomt.
• Het gemiddelde en de variabiliteit van de doorlooptijden van aanvullingen vanuit het DC.
• Het gemiddelde en de variabiliteit van de doorlooptijden voor aanvulling van de bron.
• Het vereiste minimale serviceniveau in de magazijnen.
• Het vereiste minimale serviceniveau op het DC.
• De voorraad-, bestel- en tekortkosten in elk magazijn.
• De bewaar-, bestel- en tekortkosten bij het DC.

Zoals je zou verwachten, zullen gissingen op de broekspijpen in deze situatie niet goed werken. Evenmin zal proberen het probleem te vereenvoudigen door elk echelon afzonderlijk te analyseren. Voorraden op het DC verhogen bijvoorbeeld het risico op stockouts op magazijnniveau en vice versa.

Dit probleem is duidelijk te ingewikkeld om te proberen op te lossen zonder hulp van een of ander computermodel.

Waarom standaard inventarisatietheorie slechte wiskunde is?

Met een beetje zoeken vind je modellen, tijdschriftartikelen en boeken over MEIO. Dit zijn waardevolle bronnen van informatie en inzicht, even getallen. Maar de meeste van hen vertrouwen op het hulpmiddel om het probleem te eenvoudig te maken om het schrijven en oplossen van vergelijkingen mogelijk te maken. Dit is de "Fantasie" waarnaar in de titel wordt verwezen.

Dit doen is een klassieke modelleringsmanoeuvre en is niet per se een slecht idee. Toen ik afstudeerde aan het MIT, leerde ik de waarde van het hebben van twee modellen: een klein, ruw model om als een soort vizier te dienen en een groter, nauwkeuriger model om betrouwbare getallen te produceren. Het kleinere model is gebaseerd op vergelijkingen en op theorie; het grotere model is gebaseerd op procedures en op gegevens, dwz een gedetailleerde systeemsimulatie. Modellen die gebaseerd zijn op eenvoudige theorieën en vergelijkingen kunnen slechte numerieke schattingen opleveren en zelfs hele verschijnselen over het hoofd zien. Daarentegen zullen modellen die gebaseerd zijn op procedures (bijv. "bestel tot de Max wanneer u de Min overschrijdt") en feiten (bijv. de laatste 3 jaar van de dagelijkse vraag naar artikelen) veel meer rekenkracht vergen, maar realistischere antwoorden geven. Gelukkig hebben we dankzij de cloud veel rekenkracht binnen handbereik.

Misschien wel de grootste modellering van "zonde" in de MEIO-literatuur is de veronderstelling dat eisen op alle echelons kunnen worden gemodelleerd als puur willekeurige Poisson-processen. Zelfs als het waar zou zijn op magazijnniveau, zou het verre van waar zijn op DC-niveau. Het Poisson-proces is de "witte rat van vraagmodellering" omdat het eenvoudig is en meer manipulatie van papier-en-potloodvergelijkingen mogelijk maakt. Omdat niet alle eisen Poisson-vormig zijn, resulteert dit in onrealistische aanbevelingen.

Op scenario's gebaseerde simulatie-optimalisatie

Om realisme te krijgen, moeten we dieper ingaan op de details van hoe de voorraadsystemen op elk echelon werken. Met weinig beperkingen, behalve die opgelegd door hardware, zoals de grootte van het geheugen, kunnen computerprogramma's elk niveau van complexiteit aan. Het is bijvoorbeeld niet nodig om aan te nemen dat elk van de magazijnen te maken heeft met identieke vraagstromen of dezelfde kosten heeft als alle andere.

Een computersimulatie werkt als volgt.

1. De werkelijke vraaggeschiedenis en doorlooptijdgeschiedenis worden verzameld voor elke SKU op elke locatie.
2. Waarden van voorraadparameters (bijv. Min en Max) worden geselecteerd voor proef.
3. De vraag- en aanvullingsgeschiedenissen worden gebruikt om scenario's te creëren die de invoer naar het computerprogramma weergeven dat de werkingsregels van het systeem codeert.
4. De ingangen worden gebruikt om de werking van een computermodel van het systeem aan te sturen met de gekozen parameterwaarden over een lange periode, bijvoorbeeld een jaar.
5. Voor het gesimuleerde jaar worden key performance indicators (KPI's) berekend.
6. Stappen 2-5 worden vele malen herhaald en de resultaten worden gemiddeld om parameterkeuzes te koppelen aan systeemprestaties.
7.  

Voorraadoptimalisatie voegt nog een "buitenste lus" toe aan de berekeningen door systematisch te zoeken naar de mogelijke waarden van Min en Max. Van de parameterparen die voldoen aan de artikelbeschikbaarheidsbeperking, identificeert verder zoeken de Min- en Max-waarden die resulteren in de laagste bedrijfskosten.

Figuur 1: Algemene structuur van één type voorraadsysteem op twee niveaus

Blijf op de hoogte voor onze volgende blog

BINNENKORT BESCHIKBAAR. Om een voorbeeld van een simulatie van het systeem in figuur 1 te zien, lees de tweede blog over dit onderwerp

Denk aan het probleem van het aanvullen van de voorraad. Stel dat het betreffende voorraadartikel een reserveonderdeel is, om precies te zijn. Zowel u als uw leverancier zullen een idee willen hebben van hoeveel u gaat bestellen en wanneer. En uw ERP-systeem dringt er misschien op aan dat u ook het geheim prijsgeeft.

Deterministisch model van aanvulling

De eenvoudigste manier om een fatsoenlijk antwoord op deze vraag te krijgen, is aan te nemen dat de wereld, nou ja, eenvoudig is. In dit geval betekent eenvoudig 'niet willekeurig' of, in nerdtaal, 'deterministisch'. In het bijzonder doe je alsof de willekeurige grootte en timing van de vraag in werkelijkheid een continue druppel-druppel-druppel is van een vaste grootte die met een vast interval komt, bijvoorbeeld 2, 2, 2, 2, 2, 2... Als dit onrealistisch lijkt , het is. De echte vraag ziet er misschien meer zo uit: 0, 1, 10, 0, 1, 0, 0, 0 met veel nullen, af en toe maar willekeurige pieken.

Maar eenvoud heeft zijn deugden. Als je net doet alsof de gemiddelde vraag elke dag op rolletjes loopt, is het gemakkelijk om uit te rekenen wanneer je je volgende bestelling moet plaatsen en hoeveel eenheden je nodig hebt. Stel dat uw voorraadbeleid van het type (Q,R) is, waarbij Q een vaste bestelhoeveelheid is en R een vast bestelpunt. Wanneer de voorraad daalt tot of onder het bestelpunt R, bestelt u Q-eenheden meer. Om de fantasie compleet te maken, gaan we ervan uit dat de doorlooptijd voor aanvulling ook vast is: na L dagen zullen die Q nieuwe eenheden op de plank liggen, klaar om aan de vraag te voldoen.

Alles wat u nu nodig heeft om uw vragen te beantwoorden, is de gemiddelde vraag per dag D naar het artikel. De logica gaat als volgt:

1. U begint elke aanvullingscyclus met Q-eenheden bij de hand.
2. Je put die voorraad uit met D eenheden per dag.
3. U bereikt dus het bestelpunt R na (QR)/D dagen.
4. Je bestelt dus elke (QR)/D dagen.
5. Elke aanvullingscyclus duurt (QR)/D + L dagen, dus u maakt in totaal 365D/(Q-R+LD) bestellingen per jaar.
6. Zolang de doorlooptijd L < R/D is, zult u nooit een voorraad hebben en zal uw voorraad zo klein mogelijk zijn.

Afbeelding 1 toont de grafiek van voorhanden voorraad versus tijd voor het deterministische model. Rond Smart Software verwijzen we naar deze plot als de "Deterministische zaagtand". De voorraad begint op het niveau van de laatste bestelhoeveelheid Q. Na gestaag afnemen gedurende de uitvaltijd (QR)/D, bereikt het niveau het bestelpunt R en activeert een bestelling voor nog een Q-eenheden. Gedurende de doorlooptijd L daalt de voorraad tot precies nul, dan komt de nieuwe bestelling op magische wijze aan en begint de volgende cyclus.

Afbeelding 1: deterministisch model van voorhanden voorraad

Dit model heeft twee voordelen. Het vereist niet meer dan algebra van de middelbare school en het combineert (bijna) alle relevante factoren om de twee gerelateerde vragen te beantwoorden: wanneer moeten we de volgende bestelling plaatsen? Hoeveel bestellingen plaatsen we in een jaar?

Probabilistisch model van aanvulling

Het is niet verrassend dat als we een deel van de fantasie uit het deterministische model halen, we meer bruikbare informatie krijgen. Het probabilistische model omvat alle rommelige willekeur in het echte probleem: de onzekerheid in zowel de timing als de omvang van de vraag, de variatie in de doorlooptijd van de aanvulling en de gevolgen van die twee factoren: de kans dat de beschikbare voorraad de nabestelling onderschrijdt punt, de kans dat er een stockout zal zijn, de variabiliteit in de tijd tot de volgende bestelling, en het variabele aantal uitgevoerde bestellingen in een jaar.

Het probabilistische model werkt door de gevolgen van onzekere vraag en variabele doorlooptijd te simuleren. Door de historische vraagpatronen van het item te analyseren (en waarnemingen uit te sluiten die zijn geregistreerd in een tijd waarin de vraag mogelijk fundamenteel anders was), creëren geavanceerde statistische methoden een onbeperkt aantal realistische vraagscenario's. Vergelijkbare analyse wordt toegepast op records van doorlooptijden van leveranciers. Door deze vraag- en aanbodscenario's te combineren met de operationele regels van een bepaald voorraadbeheerbeleid, ontstaan scenario's van het aantal beschikbare onderdelen. Uit deze scenario's kunnen we samenvattingen halen van de variërende intervallen tussen bestellingen.

Figuur 2 toont een voorbeeld van een probabilistisch scenario; de vraag is willekeurig en het artikel wordt beheerd met bestelpunt R = 10 en bestelhoeveelheid Q=20. Voorbij is de deterministische zaagtand; in plaats daarvan is er iets complexer en realistischer (de probabilistische trap). Tijdens de 90 gesimuleerde werkingsdagen werden er 9 bestellingen geplaatst en de tijd tussen de bestellingen varieerde duidelijk.

Met behulp van het probabilistische model worden de antwoorden op de twee vragen (hoe lang tussen orders en hoeveel in een jaar) uitgedrukt als kansverdelingen die de relatieve waarschijnlijkheid van verschillende scenario's weerspiegelen. Figuur 3 toont de verdeling van het aantal dagen tussen orders na tien jaar gesimuleerde werking. Hoewel het gemiddelde ongeveer 8 dagen is, varieert het werkelijke aantal sterk, van 2 tot 17.

In plaats van uw leverancier te vertellen dat u volgend jaar X bestellingen zult plaatsen, kunt u nu X ± Y bestellingen projecteren, en uw leverancier kent de opwaartse en neerwaartse risico's beter. Beter nog, u kunt de volledige distributie als het meest uitgebreide antwoord geven.

Figuur 2 Een probabilistisch scenario van voorhanden voorraad

Figuur 3: Verdeling van dagen tussen bestellingen

De willekeurige trap beklimmen naar grotere efficiëntie

Door verder te gaan dan het deterministische inventarismodel, ontstaan nieuwe mogelijkheden voor het optimaliseren van de bedrijfsvoering. Ten eerste maakt het probabilistische model een realistische beoordeling van het voorraadrisico mogelijk. Het eenvoudige model in afbeelding 1 houdt in dat er nooit een stockout is, terwijl probabilistische scenario's de mogelijkheid toestaan (hoewel er in afbeelding 2 slechts één close call was rond dag 70). Zodra het risico bekend is, kan software optimaliseren door de "ontwerpruimte" (dwz alle mogelijke waarden van R en Q) te doorzoeken om een ontwerp te vinden dat voldoet aan een doelniveau van voorraadrisico tegen minimale kosten. De waarde van het deterministische model in deze meer realistische analyse is dat het een goed startpunt biedt voor de zoektocht door de ontwerpruimte.

Overzicht

Moderne software geeft antwoord op operationele vragen met verschillende gradaties van detail. Aan de hand van het voorbeeld van de tijd tussen aanvullingsorders hebben we laten zien dat het antwoord bij benadering maar snel kan worden berekend met een eenvoudig deterministisch model. Maar het kan ook veel gedetailleerder worden weergegeven, waarbij alle variabiliteit wordt blootgelegd door een probabilistisch model. Wij beschouwen deze alternatieven als complementair. Het deterministische model bundelt alle sleutelvariabelen in een gemakkelijk te begrijpen vorm. Het probabilistische model biedt extra realisme dat professionals verwachten en ondersteunt effectief zoeken naar optimale keuzes van bestelpunt en bestelhoeveelheid.