“Los negocios son guerra” puede ser una metáfora exagerada, pero no carece de validez. Al igual que la “brecha de los bombarderos” y la “brecha de los misiles”, la preocupación por quedarse atrás de la competencia y la consiguiente amenaza de aniquilación siempre acechan en las mentes de los ejecutivos de negocios. Si no lo hacen, deberían hacerlo, porque no todas las brechas se solucionan. imaginario (se demostró que la brecha de los bombarderos y la brecha de los misiles no existían entre los EE.UU. y la URSS, pero la brecha de los años 1980 entre la productividad japonesa y la estadounidense era demasiado real). La diferencia entre paranoia y preocupación justificada es convertir el miedo en hechos. Esta publicación trata sobre cómo organizar su atención hacia posibles brechas en el análisis de la cadena de suministro de su empresa.

Brechas de vigilancia

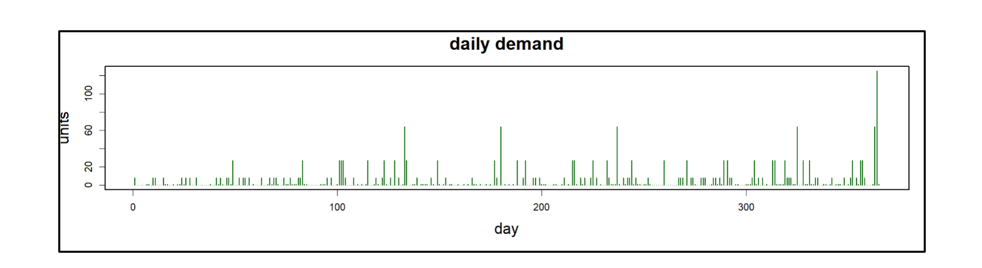
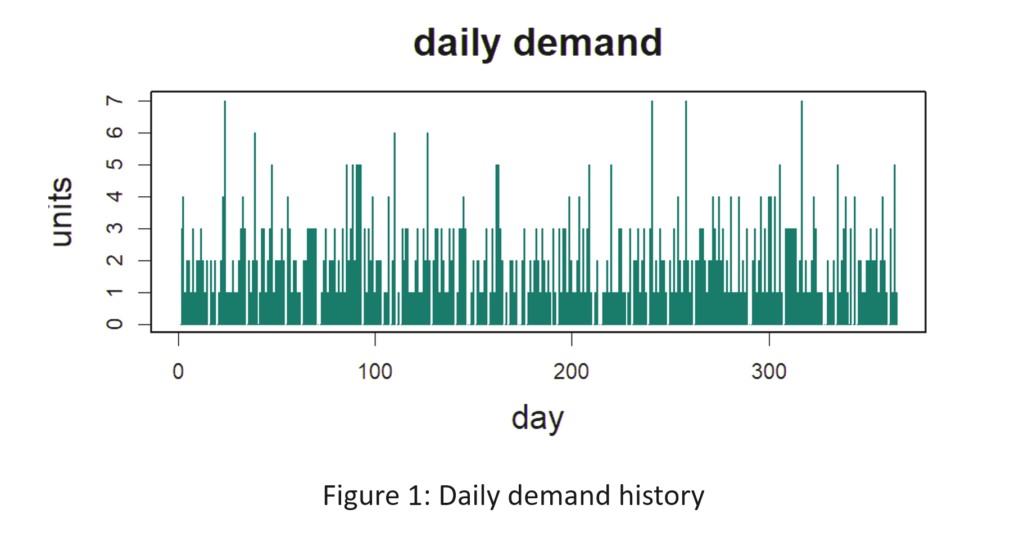
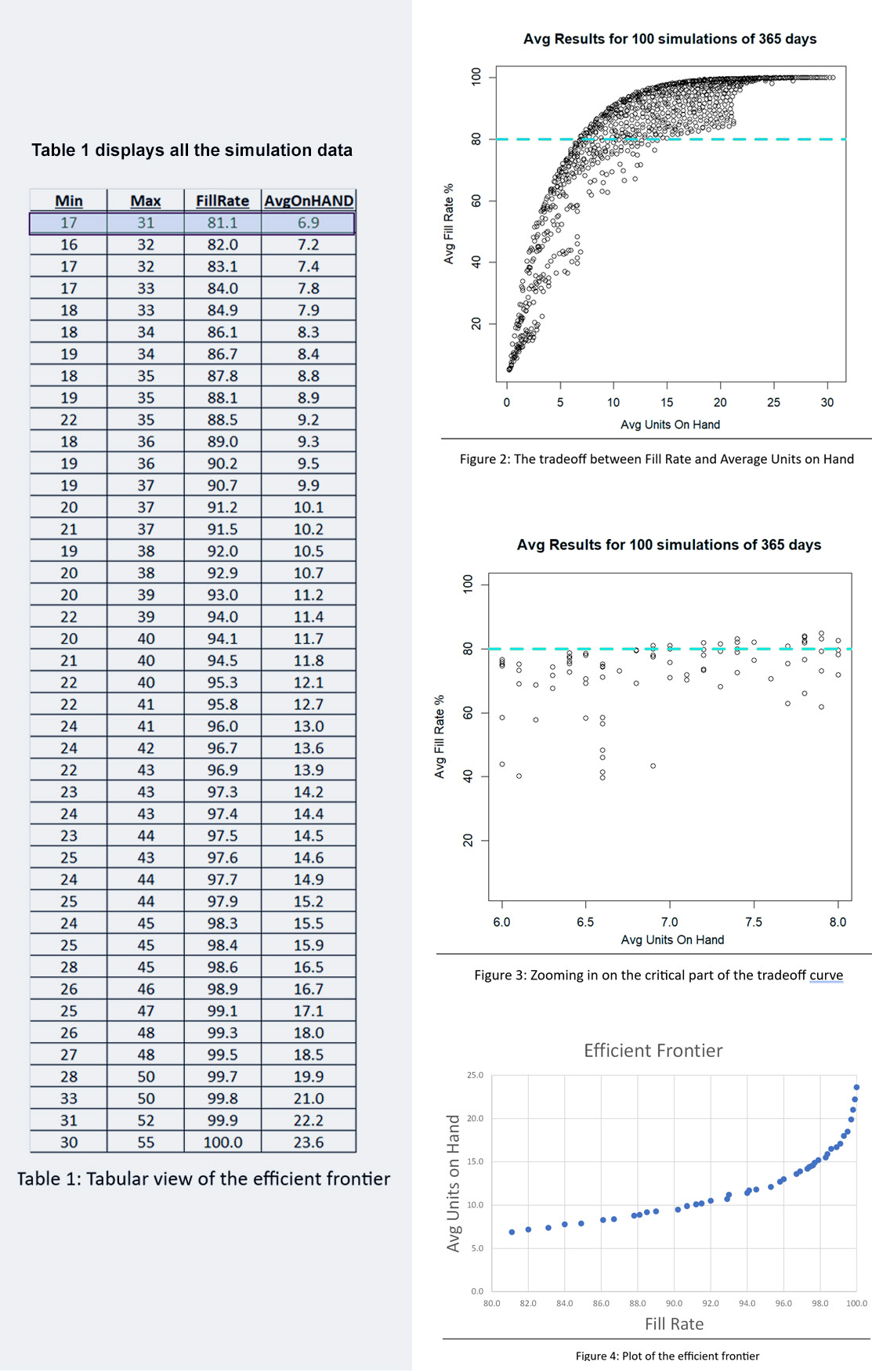
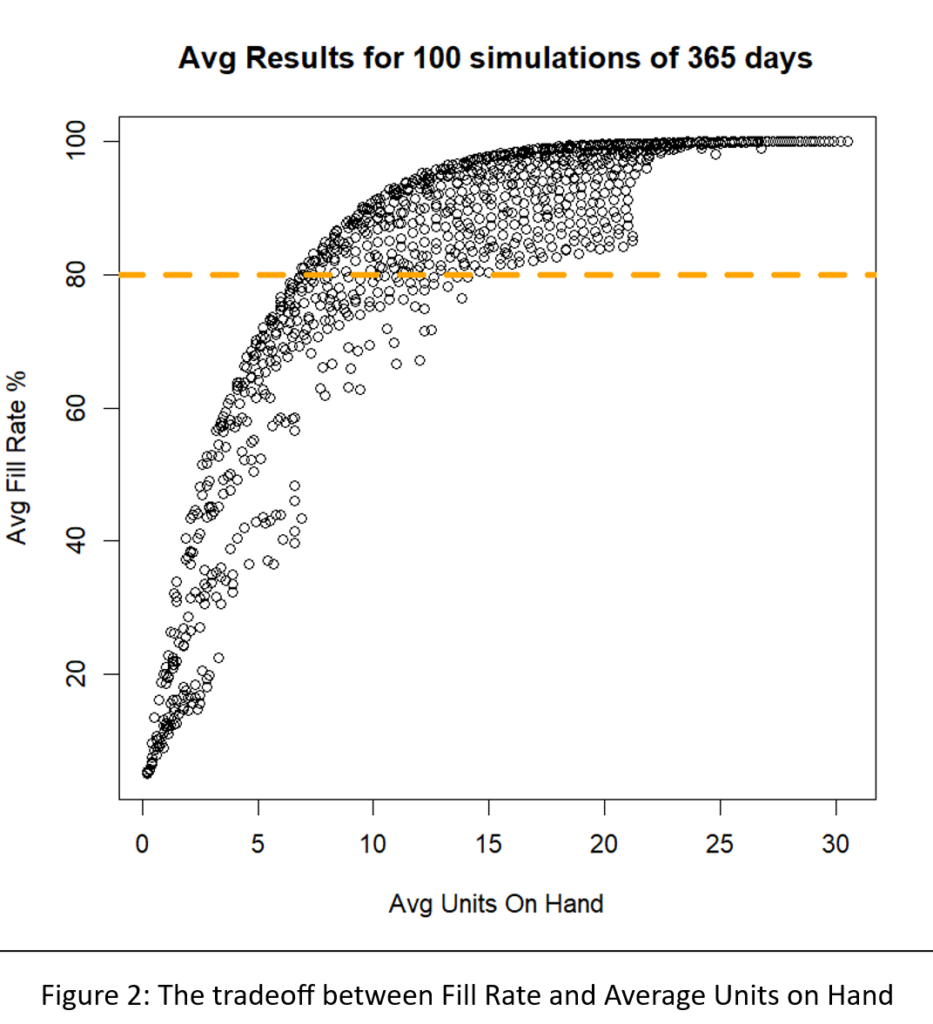
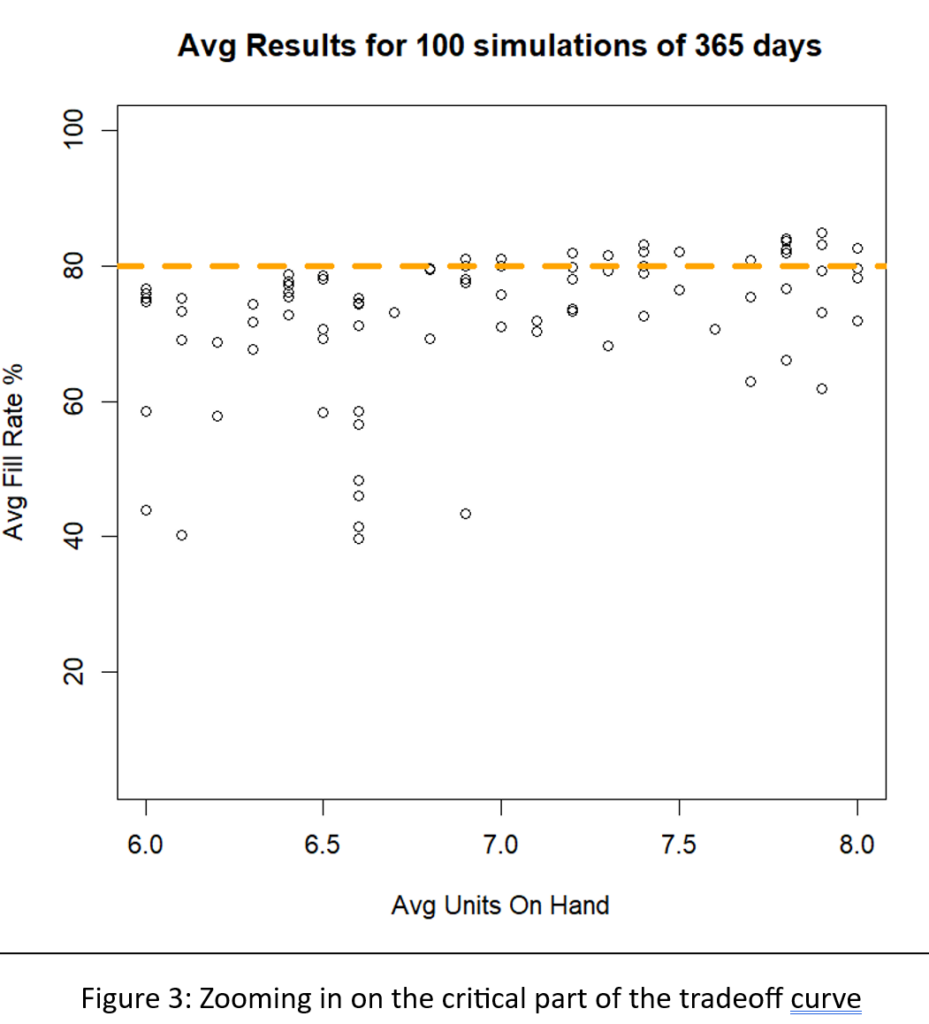
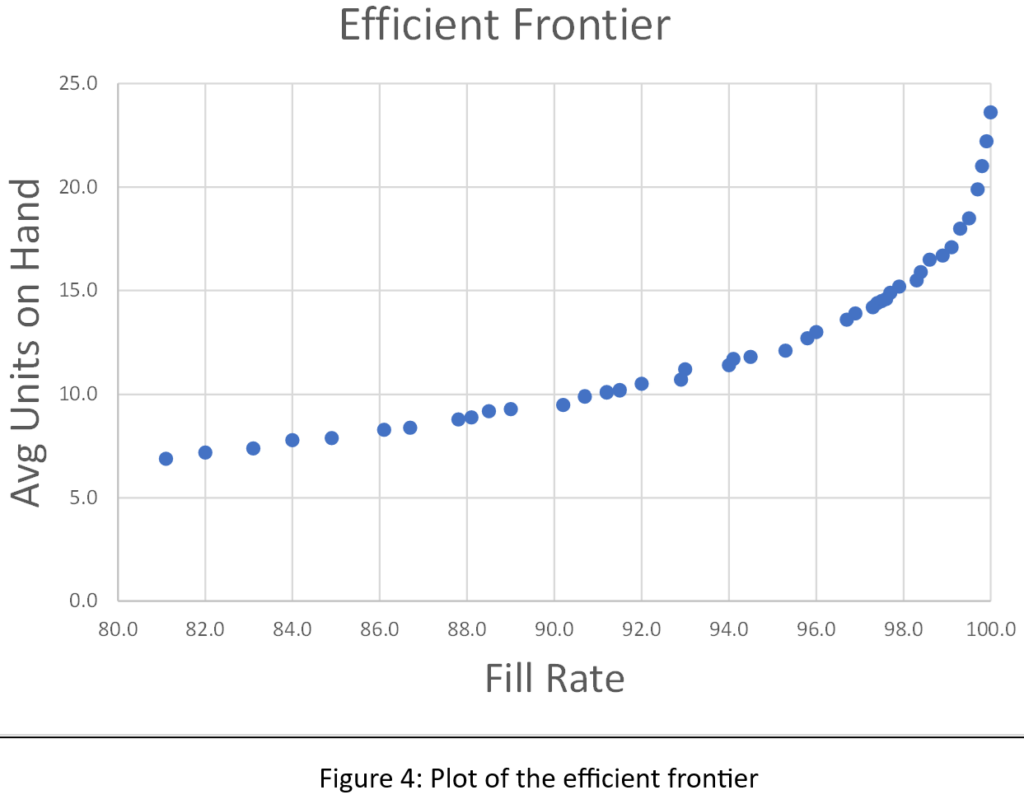
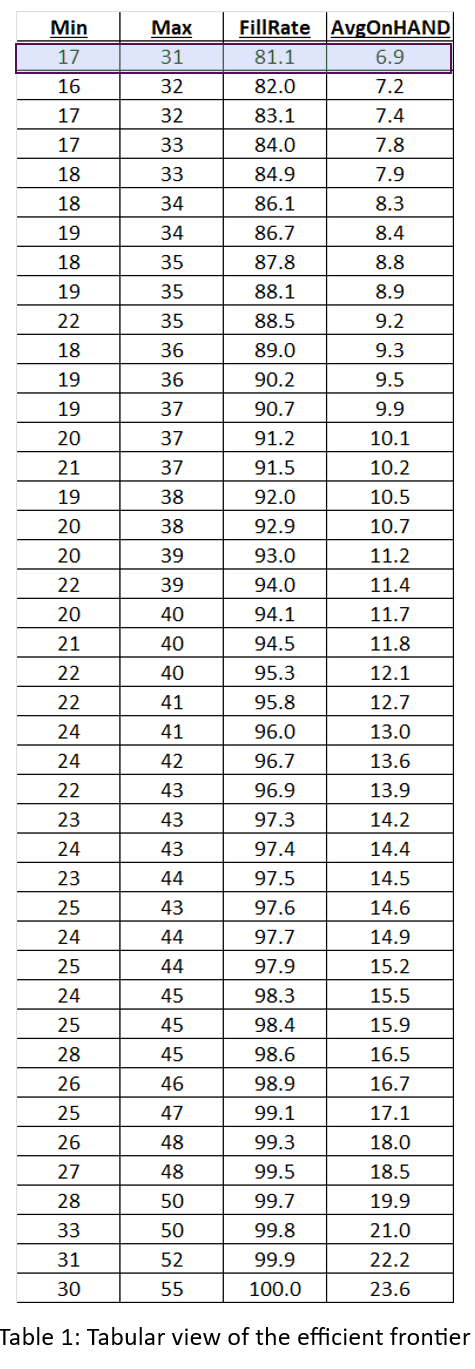
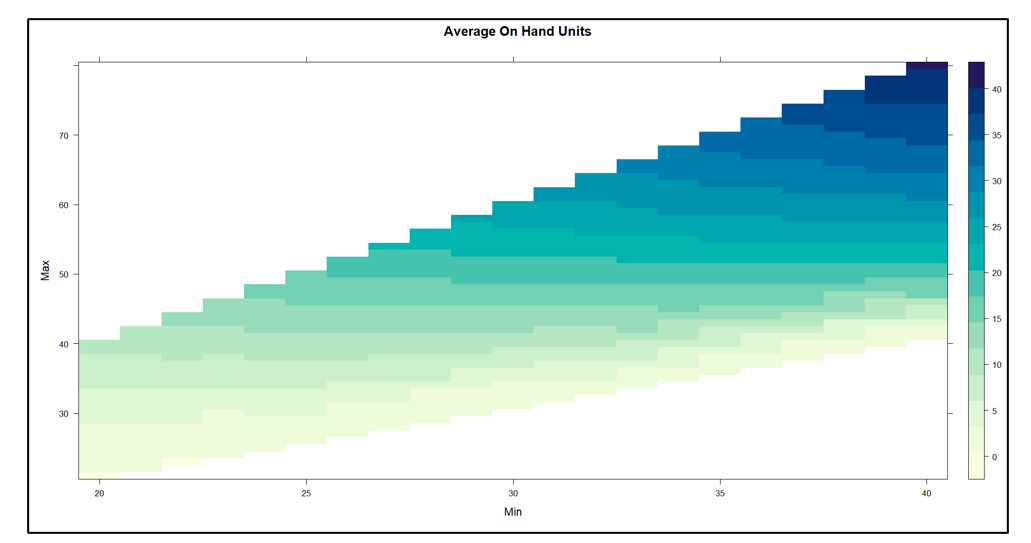
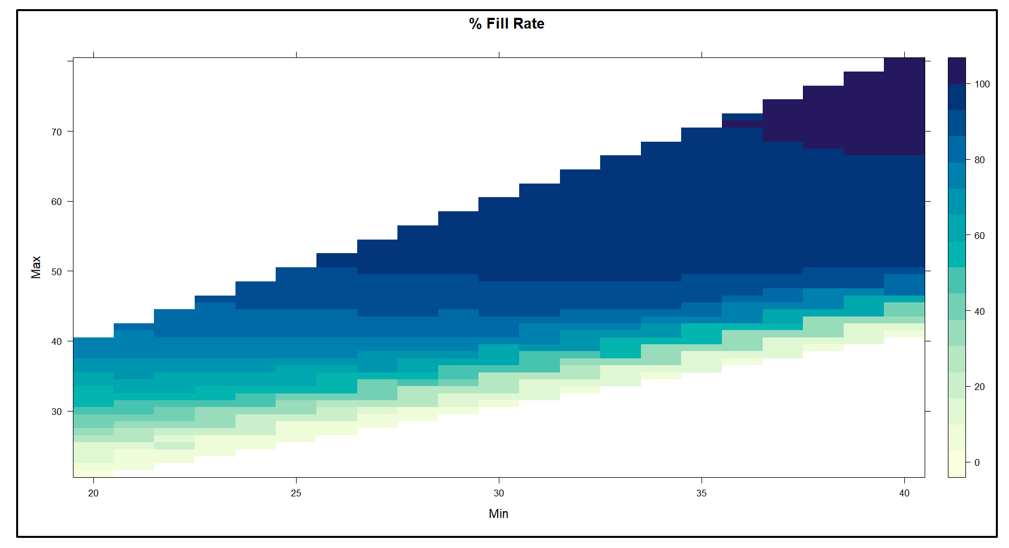
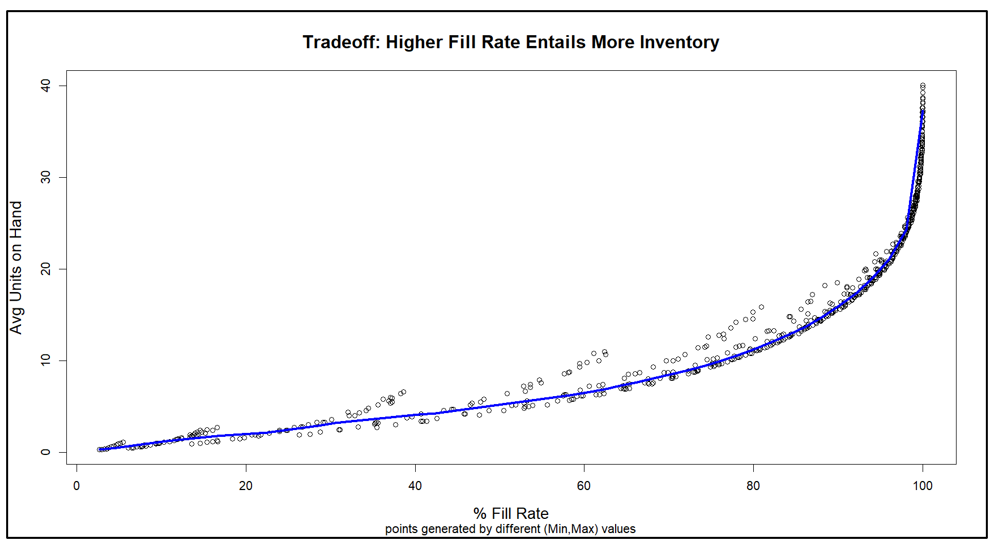
El ejército estadounidense tiene un dicho: "El tiempo dedicado al reconocimiento nunca se desperdicia". De vez en cuando, nuestro Pronosticador inteligente El blog tiene una publicación que te ayuda a girar la cabeza para ver qué sucede a tu alrededor. Un ejemplo es nuestra publicación sobre gemelos digitales, que es un tema candente en todo el mundo de la ingeniería. En resumen: utilizar simulaciones de oferta y demanda para detectar debilidades en su plan de inventario es una forma de reconocimiento de la cadena de suministro. Cerrar esta brecha de vigilancia permite a las empresas tomar medidas correctivas antes de que surja un problema real.

Brechas de conciencia situacional

Un comandante militar necesita realizar un seguimiento de lo que está disponible para su uso y de qué tan bien se está utilizando. Los informes disponibles en Analítica operativa inteligente mantenerlo actualizado sobre sus recuentos de inventario, la precisión de sus pronósticos, la capacidad de respuesta de sus proveedores y las tendencias en estas y otras áreas operativas. Sabrá exactamente cuál es su posición en una variedad de KPI de la cadena de suministro, como el nivel de servicio, las tasas de cumplimiento y la rotación de inventario. Sabrá si el desempeño real está alineado con el desempeño planificado y si el plan de inventario (es decir, qué pedir, cuándo, a quién y por qué) se cumple o se ignora.

Brechas de agilidad

El entorno empresarial puede cambiar rápidamente. Todo lo que se necesita es un camión cisterna atrapado de costado en el Canal de Suez, unos cuantos misiles balísticos antibuque en el Mar Rojo o un fenómeno meteorológico que afecte a toda la región. Estas catástrofes pueden recaer tanto sobre la cabeza de sus competidores como sobre la suya, pero ¿quién de ustedes es lo suficientemente ágil como para reaccionar primero? Informe de excepciones en Planificador de la demanda y análisis operativo inteligente puede detectar cambios importantes en el carácter de la demanda para que pueda filtrar rápidamente datos de demanda obsoletos antes de que contaminen todos sus cálculos para pronósticos de demanda u optimización de inventario. Planificador de la demanda puede avisar con antelación de un aumento o disminución pendiente de la demanda. Optimización del inventario puede ayudarle a ajustar sus tácticas de reabastecimiento de inventario para reflejar estos cambios en la demanda.

Brechas de innovación

Ya sea que te refieras a tu competencia como "Los otros chicos" o "Todos los demás" o algo que no se pueda imprimir, aquellos de los que debes preocuparte son los que siempre buscan una ventaja. Cuando elige a Smart como su socio, le brindaremos esa ventaja con soluciones predictivas innovadoras pero probadas en el campo. Smart Software ha estado innovando en modelos predictivos desde su nacimiento hace más de 40 años.

• Nuestros primeros productos introdujeron múltiples innovaciones técnicas: evaluación de la calidad del pronóstico mirando hacia el futuro, no hacia el pasado; selección automática de las mejores entre un conjunto de metodologías competitivas, aprovechando los gráficos de los primeros PC para permitir una fácil gestión de las anulaciones de las previsiones estadísticas.

• Más tarde inventamos y patentamos un enfoque radicalmente diferente para pronosticar la demanda intermitente que es característica tanto de repuestos como de bienes duraderos costosos. Nuestra tecnología fue patentada y recibió múltiples premios por mejorar drásticamente la gestión del inventario. La solución es ahora un enfoque probado en el campo utilizado por muchas empresas líderes en repuestos, MRO, repuestos de posventa y servicio de campo.

• Más recientemente, la plataforma en la nube de Smart para pronóstico de demanda, modelado predictivo, optimización de inventario y análisis, toma todos los datos relevantes que de otro modo estarían bloqueados en sus sistemas ERP o EAM, archivos externos y otras fuentes de datos dispares, y los organiza en el canalización de datos inteligente, lo estructura en nuestro modelo de datos comúny lo procesa en nuestro nube de AWS. Inteligente utiliza el poder de nuestro patentado simulaciones probabilísticas de demanda en Smart Inventory Optimization para realizar pruebas de estrés y optimizar las reglas que utiliza para administrar cada uno de los artículos de su inventario.

Es mi trabajo, junto con mi cofundador, el Dr. Nelson Hartunian, nuestro equipo de ciencia de datos y consultores académicos, continuar ampliando los límites del análisis de la cadena de suministro y brindarle los beneficios mediante la implementación continua de nuevas versiones de nuestros productos para que usted no se quede atrapado en una brecha de innovación, ni en ninguna de las otras.

Nuestros clientes generalmente se han decidido por una forma de administrar su inventario de repuestos. Al profesor que hay en mí le gustaría pensar que la política de inventario elegida fue una elección razonada entre las alternativas consideradas, pero lo más probable es que simplemente haya sucedido. Tal vez el jefe de inventario de hace mucho tiempo tenía un favorito y esa elección se mantuvo. Quizás alguien utilizó un sistema EAM o ERP que ofrecía sólo una opción. Quizás se hicieron algunas conjeturas, basándose en las condiciones del momento.

Los competidores

Muy rara vez las empresas toman estas decisiones al azar. Pero el software moderno de planificación de repuestos le permite ser más sistemático en sus elecciones. Esta publicación demuestra esa propuesta al hacer comparaciones objetivas entre tres políticas de inventario populares: Pedido hasta, Punto de reorden/Cantidad de pedido y Mín./Máx. Hablé de cada una de estas políticas en este videoblog.

• Ordene hasta. Esta es una política de revisión periódica en la que cada T días se cuenta el inventario disponible y se realiza un pedido de tamaño aleatorio para que el nivel de existencias vuelva a subir a S unidades.
• Q, R o Punto de reorden/Cantidad de pedido. Q, R es una política de revisión continua en la que todos los días se contabiliza el inventario. Si hay Q o menos unidades disponibles, se realiza un pedido de tamaño fijo por R unidades más.
• Mínimo máximo es otra política de revisión continua en la que todos los días se cuenta el inventario. Si hay unidades mínimas o menos disponibles, se realiza un pedido para que el nivel de existencias vuelva a alcanzar las unidades máximas.

La teoría del inventario dice que estas opciones se enumeran en orden creciente de efectividad. La primera opción, Ordenar hasta, es claramente la más sencilla y barata de implementar, pero hace la vista gorda a lo que sucede durante largos períodos de tiempo. Imponer un intervalo de tiempo específico entre órdenes lo hace, en teoría, menos flexible. Por el contrario, las dos opciones de revisión continua vigilan lo que sucede todo el tiempo, para que puedan reaccionar más rápido ante posibles desabastecimientos. La opción Min/Max es, en teoría, más flexible que la opción que utiliza una cantidad fija de reorden porque el tamaño del pedido cambia dinámicamente para adaptarse a la demanda.

Esa es la teoría. Esta publicación examina la evidencia de comparaciones directas para verificar la teoría y establecer cifras concretas sobre el desempeño relativo de las tres políticas.

El significado de "mejor"

¿Cómo debemos llevar la puntuación en este torneo? Si es un lector habitual de este blog de Smart Forecaster, sabrá que el núcleo de la planificación del inventario es un tira y afloja entre dos objetivos opuestos: mantener el inventario reducido versus mantener las métricas de disponibilidad de los artículos, como el nivel de servicio alto.

Para simplificar las cosas, calcularemos “un número para gobernarlos a todos”: el costo operativo promedio. La póliza ganadora será la que tenga el promedio más bajo.

Este promedio es la suma de tres componentes: el costo de mantener el inventario (“costo de mantener”), el costo de ordenar unidades de reabastecimiento (“costo de ordenar”) y el costo de perder una venta (“costo de escasez”). Para concretar las cosas, utilizamos los siguientes supuestos:

• Cada pieza de servicio está valorada en $1.000.
• El costo de tenencia anual es 10% del valor del artículo, o $100 por año por unidad.
• Procesar cada pedido de reabastecimiento cuesta $20 por pedido.
• Cada unidad demandada pero no proporcionada cuesta el valor de la pieza, $1.000.

Para simplificar, nos referiremos al costo operativo promedio simplemente como "el costo".

Por supuesto, el costo promedio más bajo se puede lograr saliendo del negocio. Por lo tanto, la competencia requería una limitación de rendimiento en la disponibilidad de los artículos: cada opción tenía que lograr una tasa de cumplimiento de al menos 99%.

Las alternativas se resisten

Un elemento clave del contexto es si los desabastecimientos provocan pérdidas o pedidos atrasados. Suponiendo que la pieza de servicio en cuestión es crítica, asumimos que los pedidos no ejecutados se pierden, lo que significa que un competidor completa el pedido. En un entorno de MRO, esto significará un tiempo de inactividad adicional debido al desabastecimiento.

Para comparar las alternativas, utilizamos nuestro motor de modelado predictivo para ejecutar una gran cantidad de Simulaciones de Montecarlo. Cada simulación implicó especificar los valores de los parámetros de cada póliza (por ejemplo, valores mínimos y máximos), generar un escenario de demanda, introducirlo en la lógica de la póliza y medir el costo resultante promediado durante 365 días de operación. Repetir este proceso 1.000 veces y promediar los 1.000 costos resultantes dio el resultado final para cada póliza.  

Para que la comparación fuera justa, cada alternativa debía diseñarse para obtener el mejor rendimiento. Entonces buscamos en el “espacio de diseño” de cada póliza para encontrar el diseño con el menor costo. Esto requirió repetir el proceso descrito en el párrafo anterior para muchos pares de valores de parámetros e identificar el par que produce el costo operativo anual promedio perdido.

Usando los algoritmos en Optimización del inventario (SÍO^MT) realizamos comparaciones directas bajo los siguientes supuestos sobre la oferta y la demanda:

• Se supuso que la demanda de artículos era intermitente y muy variable, pero relativamente simple en el sentido de que no había tendencia ni estacionalidad, como suele ocurrir con las piezas de repuesto. La demanda media diaria fue de 5 unidades con una desviación estándar grande de 13 unidades. La Figura 1 muestra una muestra de la demanda de un año. Hemos elegido un patrón de demanda muy desafiante, en el que algunos días tienen de 10 a 20 veces la demanda promedio.

Figura 1: Se supuso que la demanda diaria de piezas era intermitente y muy intensa.

​​

• Los plazos de reabastecimiento de los proveedores fueron de 14 días (75%) en ese momento y de 21 días en el resto. Esto refleja el hecho de que siempre hay incertidumbre en la cadena de suministro.

Y el ganador es…

¿Era correcta la teoría? Un poco sorta'.

La Tabla 1 muestra los resultados de los experimentos de simulación. Para cada una de las tres políticas en competencia, muestra el costo operativo anual promedio, el margen de error (técnicamente, un intervalo de confianza aproximado de 95% para el costo medio) y las mejores opciones aparentes para los valores de los parámetros.

Tabla 1: Resultados de las comparaciones simuladas

Por ejemplo, el costo promedio de la póliza (T,S) cuando T se fija en 30 días fue de $41,680. Pero el Más/Menos implica que los resultados son compatibles con un costo “real” (es decir, la estimación de un número infinito de simulaciones) de entre $39,890 y $43,650. La razón por la que existe tanta incertidumbre estadística es la naturaleza extremadamente elevada de la demanda en este ejemplo.

El Cuadro 1 dice que, en este ejemplo, las tres políticas están en línea con las expectativas. Sin embargo, conclusiones más útiles serían:

1. Las tres políticas son notablemente similares en cuanto a costo promedio. Mediante una elección inteligente de los valores de los parámetros, se pueden obtener buenos resultados con cualquiera de las tres políticas.
2. Lo que no se muestra en el Cuadro 1, pero se desprende claramente de los resultados detallados de la simulación, es que las malas elecciones de valores de parámetros pueden ser desastrosas para cualquier política.
3. Vale la pena señalar que a la política de revisión periódica (T,S) no se le permitió optimizar sobre posibles valores de T. Fijamos T en 30 para imitar lo que es común en la práctica, pero aquellos que usan la política de revisión periódica deberían considerar otras revisiones. períodos. Un experimento adicional fijó el período de revisión en T = 7 días. El costo promedio en este escenario se minimizó en $36,551 ± $1,668 con S = 343. Este resultado es mejor que el de T = 30 días.
4. Debemos tener cuidado de no generalizar demasiado estos resultados. Dependen de los valores supuestos de los tres parámetros de costos (mantenimiento, pedidos y escasez) y del carácter del proceso de demanda.
5. Es posible ejecutar experimentos como los que se muestran aquí automáticamente en Optimización del inventario. Esto significa que usted también podrá explorar opciones de diseño de manera rigurosa.

Aquellos de ustedes que siguen temas candentes estarán familiarizados con el término "gemelo digital". Aquellos que han estado demasiado ocupados con el trabajo tal vez quieran seguir leyendo y ponerse al día.

¿Qué es un gemelo digital?

Si bien existen varias definiciones de gemelo digital, aquí hay una que funciona bien:

Un gemelo digital es una dinámica copia virtual de un activo físico, proceso, sistema o entorno que se parece y se comporta de manera idéntica a su contraparte del mundo real. Un gemelo digital ingiere datos y replica procesos así que puedes predecir posibles resultados de rendimiento y problemas que podría sufrir el producto del mundo real. [Fuente: unidad.com]. Para obtener información adicional, puede visitar Mckinsey.com.

¿Cuál es la diferencia entre un gemelo digital (en adelante DT) y un modelo? Principalmente, un DT se conecta a datos en tiempo real para mantener el modelo como una representación actualizada del sistema con el que está trabajando.

Nuestros productos actuales podrían denominarse “DT en cámara lenta” porque generalmente se usan con datos que no están en tiempo real (aunque no con datos obsoletos, ya que se actualizan durante la noche) y se aplican a problemas como planificar las compras de materias primas del próximo trimestre o establecer parámetros de inventario durante un mes o más.

¿La gente utiliza gemelos digitales en mi industria?

Mi impresión es que la penetración de los DT puede ser mayor en las industrias aeroespacial y nuclear. La mayoría de nuestros clientes están en otros lugares: en la fabricación, la distribución y los servicios públicos como el transporte y la energía. Pronto ofreceremos nuevos productos que se acercarán más a la definición estricta de un DT que está íntimamente conectado con el sistema que representa.

Vista previa de DT

La mayoría de los usuarios de Smart Inventory Optimization™ (SIO) ejecuta la aplicación periódicamente, normalmente mensualmente. SIO analiza la demanda actual de artículos de inventario y los plazos de entrega recientes de los proveedores, convirtiéndolos en escenarios de oferta y demanda, respectivamente. Luego, los usuarios, ya sea de forma interactiva (para artículos individuales) o automáticamente (a escala), establecen parámetros de control de inventario que proporcionarán el rendimiento promedio a largo plazo que desean, equilibrando los objetivos competitivos de minimizar el inventario y al mismo tiempo garantizar un nivel suficiente de disponibilidad de artículos.

Smart Supply Planner (SSP) opera de forma más inmediata para reaccionar ante contingencias. Cualquier día podría generar un pedido anómalo que aumente la demanda, como cuando un nuevo cliente realiza un pedido de almacenamiento inicial sorprendente. O un proveedor clave podría experimentar un problema en su fábrica y verse obligado a retrasar el envío de sus pedidos de reabastecimiento planificados. A largo plazo, estas contingencias se promedian y justifican las recomendaciones que surgen de SIO. Sin embargo, SSP le brindará una forma de reaccionar a corto plazo para aprovechar oportunidades o esquivar balas.

En esencia, SSP opera como SIO en el sentido de que está impulsado por escenarios. Las diferencias son que utiliza horizontes de planificación cortos y condiciones iniciales en tiempo real como base para sus simulaciones del desempeño del sistema de inventario. Luego brindará recomendaciones en tiempo real para intervenciones que compensen las perturbaciones causadas por las contingencias. Estos incluirían cancelar o acelerar las órdenes de reabastecimiento.

Resumen

Los gemelos digitales le permiten probar planes "in silico" antes de implementarlos en la fábrica o el almacén. En esencia, se encuentran los modelos matemáticos de su operación, pero conectados a datos en tiempo real. Proporcionan una “zona de pruebas digital” en la que puedes probar ideas y obtener predicciones inmediatas sobre qué tan bien funcionarán. Mucho más que una hoja de cálculo, las DT pronto serán la herramienta clave en su caja de herramientas de planificación de inventario.

Algunas empresas invierten en software que les ayude a gestionar su inventario, ya sean repuestos o productos terminados. Pero un número sorprendente de personas juegan el juego de adivinar el inventario todos los días, confiando en un “tripa dorada” imaginario o en la simple suerte para establecer sus parámetros de control de inventario. Pero, ¿qué tipo de resultados espera con ese enfoque?

¿Qué tan bueno eres para intuir los valores correctos? Esta publicación de blog lo desafía a adivinar los mejores valores mínimos y máximos para un artículo de inventario hipotético. Le mostraremos su historial de demanda, le brindaremos algunos datos relevantes, luego podrá elegir los valores mínimos y máximos y ver qué tan bien funcionarían. ¿Listo?

El reto

La Figura 1 muestra el historial de demanda diaria del artículo. La demanda promedio es de 2 unidades por día. El plazo de reposición es de 10 días constantes (lo cual no es realista pero juega a su favor). Los pedidos que no se pueden completar inmediatamente desde el stock no se pueden retrasar y se pierden. Desea lograr al menos una tasa de cumplimiento de 80%, pero no a cualquier costo. También desea minimizar la cantidad promedio de unidades disponibles y al mismo tiempo lograr al menos una tasa de llenado de 80%. ¿Qué valores mínimos y máximos producirían una tasa de llenado del 80% con el número promedio más bajo de unidades disponibles? [Grabe sus respuestas para comprobarlas más tarde. La solución aparece a continuación, al final del artículo.]

Calcular los mejores valores mínimos y máximos

La forma de determinar los mejores valores es utilizar un gemelo digital, también conocido como simulación de Monte Carlo. El análisis crea una multitud de escenarios de demanda y los pasa a través de la lógica matemática del sistema de control de inventario para ver qué valores tomarán los indicadores clave de desempeño (KPI).

Construimos un gemelo digital para este problema y lo ejercitamos sistemáticamente con 1085 pares de valores mínimos y máximos. Para cada par, simulamos 365 días de funcionamiento un total de 100 veces. Luego promediamos los resultados para evaluar el desempeño del par Mínimo/Máximo en términos de dos KPI: tasa de cumplimiento e inventario disponible promedio.

La Figura 2 muestra los resultados. La compensación inherente entre el tamaño del inventario y la tasa de cumplimiento es clara en la figura: si desea una tasa de cumplimiento más alta, debe aceptar un inventario más grande. Sin embargo, en cada nivel de inventario hay un rango de tasas de llenado, por lo que el juego consiste en encontrar el par mínimo/máximo que produzca la tasa de llenado más alta para cualquier tamaño de inventario determinado.

Una forma diferente de interpretar la Figura 2 es centrarse en la línea verde discontinua que marca la tasa de llenado objetivo del 80%. Hay muchos pares Min/Max que pueden alcanzar cerca del objetivo 80%, pero difieren en el tamaño del inventario de aproximadamente 6 a aproximadamente 8 unidades. La Figura 3 amplía esa región de la Figura 2 para mostrar una gran cantidad de pares Mín/Máx que son competitivos.

Clasificamos los resultados de las 1.085 simulaciones para identificar lo que los economistas llaman la frontera eficiente. La frontera eficiente es el conjunto de pares mínimo/máximo más eficientes para explotar el equilibrio entre la tasa de llenado y las unidades disponibles. Es decir, es una lista de pares mínimo/máximo que proporciona la forma más económica de lograr cualquier tasa de llenado deseada, no solo 80%. La Figura 4 muestra la frontera eficiente para este problema. Moviéndose de izquierda a derecha, puede leer el precio más bajo que tendría que pagar (medido por el tamaño promedio del inventario) para lograr cualquier tasa de cumplimiento objetivo. Por ejemplo, para lograr una tasa de llenado del 90%, tendría que tener un inventario promedio de aproximadamente 10 unidades.

Las figuras 2, 3 y 4 muestran resultados para varios pares Mín/Máx, pero no muestran los valores de Mín y Máx detrás de cada punto. La Tabla 1 muestra todos los datos de la simulación: los valores mínimo, máximo, unidades promedio disponibles y tasa de llenado. La respuesta al juego de adivinanzas está resaltada en la primera línea de la tabla: Mín=7 y Máx=13¹. ¿Obtuviste la respuesta correcta o algo parecido?²? ¿Quizás llegaste a la frontera eficiente?

Conclusiones

Tal vez tuviste suerte, o tal vez tengas un intestino dorado, pero es más probable que no hayas obtenido la respuesta correcta, y es aún más probable que ni siquiera lo hayas intentado. Encontrar la respuesta correcta es extremadamente difícil sin utilizar el gemelo digital. Adivinar no es profesional.

Un paso adelante de las conjeturas es “adivinar y ver”, en el que implementas tu conjetura y luego esperas un tiempo (¿meses?) para ver si te gustan los resultados. Esa táctica es al menos “científica”, pero es ineficiente.

Ahora considere el esfuerzo de encontrar los mejores pares (Min, Max) para miles de artículos. A esa escala, hay aún menos justificación para jugar el Juego de Adivinar el Inventario. La respuesta correcta es jugarlo... Inteligente³.

¹ Esta respuesta tiene una ventaja, ya que logra una tasa de llenado un poco mayor que 80% con un tamaño de inventario promedio más bajo que la combinación Mín./Máx. que alcanzó exactamente 80%. En otras palabras, (7,13) está en la frontera eficiente.

² Debido a que estos resultados provienen de una simulación en lugar de una ecuación matemática exacta, existe un cierto margen de error asociado con cada tasa de llenado y nivel de inventario estimados. Sin embargo, debido a que los resultados promedio se basaron en 100 simulaciones cada 365 días, los márgenes de error son pequeños. En todos los experimentos, los errores estándar promedio en la tasa de llenado y el inventario medio fueron, respectivamente, sólo 0,009% y 0,129 unidades.

³ En caso de que no lo sepas, uno de los fundadores de Smart Software fue... Charlie Smart.

Acto de equilibrio

La gestión del inventario, como la gestión de cualquier cosa, implica equilibrar prioridades en competencia. ¿Quieres un inventario ajustado? ¡Sí! ¿Quiere poder decir "Está en stock" cuando un cliente quiere comprar algo? ¡Sí!

¿Pero puedes tener ambas cosas? Sólo hasta cierto punto. Si se inclina por inclinar su inventario de manera demasiado agresiva, corre el riesgo de quedarse sin existencias. Si eliminas los desabastecimientos, creas un exceso de inventario. Se ve obligado a encontrar un equilibrio satisfactorio entre los dos objetivos en competencia: un inventario reducido y una alta disponibilidad de artículos.

Lograr un equilibrio

¿Cómo se logra ese equilibrio? Demasiados planificadores de inventarios “intuyen” el camino hacia algún tipo de respuesta. O encuentran una respuesta inteligente una vez y esperan que tenga una fecha de caducidad lejana y sigan usándola mientras se concentran en otros problemas. Desafortunadamente, los cambios en la demanda y/o los cambios en el desempeño de los proveedores y/o los cambios en las prioridades de su propia empresa dejarán obsoletos los viejos planes de inventario y lo devolverán al punto de partida.

Es inevitable que todo plan tenga una vida útil y deba actualizarse. Sin embargo, definitivamente no es una buena práctica reemplazar una suposición por otra. En cambio, cada ciclo de planificación debería aprovechar el software moderno de la cadena de suministro para reemplazar las conjeturas con análisis basados en hechos utilizando matemáticas de probabilidad.

Conocete a ti mismo

Lo único que el software no puede hacer es calcular la mejor respuesta sin conocer sus prioridades. ¿Cuánto prioriza el inventario eficiente sobre la disponibilidad de artículos? El software predecirá los niveles de inventario y disponibilidad causados por cualquier decisión que tome sobre cómo administrar cada artículo en su inventario, pero solo usted puede decidir si un conjunto determinado de indicadores clave de desempeño es consistente con lo que desea.

Saber lo que quieres en un sentido general es fácil: lo quieres todo. Pero saber qué prefiere al comparar escenarios específicos es más difícil. Es útil poder ver una variedad de posibilidades realizables y reflexionar sobre cuál parece mejor cuando se presentan una al lado de la otra.

Ver lo que sigue

El software de cadena de suministro puede brindarle una visión de la curva de compensación. En general, usted sabe que el inventario reducido y la alta disponibilidad de artículos se compensan entre sí, pero ver las curvas de compensación de artículos específicos agudiza su atención.

¿Por qué hay una curva? Porque tienes opciones sobre cómo gestionar cada elemento. Por ejemplo, si verifica el estado del inventario continuamente, ¿qué valores asignará a los Mínimo y máximo valores que rigen cuándo pedir reabastecimientos y cuánto pedir. La curva de compensación surge porque elegir diferentes valores mínimos y máximos conduce a diferentes niveles de inventario disponible y diferentes niveles de disponibilidad de artículos, por ejemplo, medidos por tasa de relleno.

Un escenario para el análisis

Para ilustrar estas ideas, utilicé un gemelo digital  para estimar cómo se comportarían varios valores de Min y Max en un escenario particular. El escenario se centró en una pieza de repuesto teórica con una demanda puramente aleatoria que tenía un nivel moderadamente alto de intermitencia (37% de días con demanda cero). Los plazos de reposición fueron de entre 7 y 14 días. Los valores Min y Max fueron variados sistemáticamente: Min de 20 a 40 unidades, Max de Min+1 unidades a 2xMin unidades. Cada par (Min,Max) se simuló durante 365 días de operación un total de 1000 veces, luego los resultados se promediaron para estimar tanto el número promedio de unidades disponibles como la tasa de cumplimiento, es decir, el porcentaje de demandas diarias que se cumplieron inmediatamente desde existencias. Si no había stock disponible, se encontraba pendiente de entrega.

Resultados

El experimento produjo dos tipos de resultados:

• Gráficos que muestran la relación entre los valores mínimos y máximos y dos indicadores clave de rendimiento: tasa de cumplimiento y unidades promedio disponibles.
• Una curva de compensación que muestra cómo la tasa de cumplimiento y las unidades disponibles se compensan entre sí.

La Figura 1 muestra el inventario disponible en función de los valores de Min y Max. El experimento arrojó niveles manuales que oscilaban entre cerca de 0 y aproximadamente 40 unidades. En general, mantener Min constante y aumentar Max da como resultado más unidades disponibles. La relación con Min es más compleja: mantener Max constante y aumentar Min primero aumenta el inventario, pero en algún momento lo reduce.

La Figura 2 muestra la tasa de llenado en función de los valores de Min y Max. El experimento arrojó niveles de tasa de llenado que van desde cerca de 0% hasta 100%. En general, las relaciones funcionales entre la tasa de llenado y los valores de Min y Max reflejaron las de la Figura 1.

La Figura 3 destaca el punto clave, mostrando cómo variar Min y Max produce un emparejamiento perverso de los indicadores clave de desempeño. En términos generales, los valores de Min y Max que maximizan la disponibilidad del artículo (tasa de cumplimiento) son los mismos valores que maximizan el costo del inventario (unidades promedio disponibles). Este patrón general está representado por la curva azul. Los experimentos también produjeron algunas ramificaciones de la curva azul que están asociadas con malas elecciones de Min y Max, en el sentido de que otras opciones las dominan al producir la misma tasa de cumplimiento con un inventario más bajo.

Conclusiones

La Figura 3 deja en claro que su elección de cómo administrar un artículo del inventario lo obliga a equilibrar el costo del inventario y la disponibilidad del artículo. Puede evitar algunas combinaciones ineficientes de valores mínimos y máximos, pero no puede escapar de la compensación.

El lado bueno de esta realidad es que no tienes que adivinar qué sucederá si cambias tus valores actuales de Min y Max por otros. El software le dirá cuánto le permitirá comprar esa mudanza y cuánto le costará. Puedes quitarte el sombrero de Guestimator y hacer lo tuyo con confianza.

Figura 1 Inventario disponible en función de los valores mínimos y máximos

Figura 2 Tasa de llenado en función de los valores mínimo y máximo

Figura 3 Curva de compensación entre tasa de cumplimiento e inventario disponible