Measuring the accuracy of forecasts is an undeniably important part of the demand planning process. This forecasting scorecard could be built based on one of two contrasting viewpoints for computing metrics. The error viewpoint asks, “how far was the forecast from the actual?” The accuracy viewpoint asks, “how close was the forecast to the actual?” Both are valid, but error metrics provide more information.

Accuracy is represented as a percentage between zero and 100, while error percentages start at zero but have no upper limit. Reports of MAPE (mean absolute percent error) or other error metrics can be titled “forecast accuracy” reports, which blurs the distinction.  So, you may want to know how to convert from the error viewpoint to the accuracy viewpoint that your company espouses.  This blog describes how with some examples.

Accuracy metrics are computed such that when the actual equals the forecast then the accuracy is 100% and when the forecast is either double or half of the actual, then accuracy is 0%. Reports that compare the forecast to the actual often include the following:

• The Actual
• The Forecast
• Unit Error = Forecast – Actual
• Absolute Error = Absolute Value of Unit Error
• Absolute % Error = Abs Error / Actual, as a %
• Accuracy % = 100% – Absolute % Error

Look at a couple examples that illustrate the difference in the approaches. Say the Actual = 8 and the forecast is 10.

Unit Error is 10 – 8 = 2

Absolute % Error = 2 / 8, as a % = 0.25 * 100 = 25%

Accuracy = 100% – 25% = 75%.

Now let’s say the actual is 8 and the forecast is 24.

Unit Error is 24– 8 = 16

Absolute % Error = 16 / 8 as a % = 2 * 100 = 200%

Accuracy = 100% – 200% = negative is set to 0%.

In the first example, accuracy measurements provide the same information as error measurements since the forecast and actual are already relatively close. But when the error is more than double the actual, accuracy measurements bottom out at zero. It does correctly indicate the forecast was not at all accurate. But the second example is more accurate than a third, where the actual is 8 and the forecast is 200. That’s a distinction a 0 to 100% range of accuracy doesn’t register. In this final example:

Unit Error is 200 – 8 = 192

Absolute % Error = 192 / 8, as a % = 24 * 100 = 2,400%

Accuracy = 100% – 2,400% = negative is set to 0%.

Error metrics continue to provide information on how far the forecast is from the actual and arguably better represent forecast accuracy.

We encourage adopting the error viewpoint. You simply hope for a small error percentage to indicate the forecast was not far from the actual, instead of hoping for a large accuracy percentage to indicate the forecast was close to the actual.  This shift in mindset offers the same insights while eliminating distortions.

Summary

Smart Software’s advanced supply chain analytics exploits multiple advanced methods. Two of the most important are “statistical bootstrapping” and “Monte Carlo simulation”. Since both involve lots of random numbers flying around, folks sometimes get confused about which is which and what they are good for. Hence, this note. Bottom line up front: Statistical bootstrapping generates demand scenarios for forecasting. Monte Carlo simulation uses the scenarios for inventory optimization.

Bootstrapping

Bootstrapping, also called “resampling” is a method of computational statistics that we use to create demand scenarios for forecasting. The essence of the forecasting problem is to expose possible futures that your company might confront so you can work out how to manage business risks. Traditional forecasting methods focus on computing “most likely” futures, but they fall short of presenting the full risk picture. Bootstrapping provides an unlimited number of realistic what-if scenarios.

Bootstrapping does this without making unrealistic assumptions about the demand, i.e., that it is not intermittent, or that it has a bell-shaped distribution of sizes. Those assumptions are crutches to make the math simpler, but the bootstrap is a procedure,  not an equation, so it doesn’t need such simplifications.

For the simplest demand type, which is a stable randomness with no seasonality or trend, bootstrapping is dead easy. To get a reasonable idea of what a single future demand value might be, pick one of the historical demands at random. To create a demand scenario, make multiple random selections from the past and string them together. Done. It is possible to add a little more realism by “jittering” the demand values, i.e., adding or subtracting a bit of additional randomness to each one, but even that is simple.

Figure 1 shows a simple bootstrap. The first line is a short sequence of historical demand for an SKU. The following lines show scenarios of future demand created by randomly selecting values from the demand history. For instance, the next three demand might be (0, 14, 6), or (2, 3, 5), etc.

Figure 1: Example of demand scenarios generated by a simple bootstrap

Higher frequency operations such as daily forecasting bring with them more complex demand patterns, such as double seasonality (e.g., day-of-week and month-of-year) and/or trend. This challenged us to invent a new generation of bootstrapping algorithms. We recently won a US Patent for this breakthrough, but the essence is as described above.

Monte Carlo Simulation

Monte Carlo is famous for its casinos, which, like bootstrapping, invoke the idea of randomness. Monte Carlo methods go back a long way, but the modern impetus came with the need to do some hairy calculations about where neutrons would fly when an A-bomb explodes.

The essence of Monte Carlo analysis is this: “Our problem is too complicated to analyze with paper-and-pencil equations. So, let’s write a computer program that codes the individual steps of the process, put in the random elements (e.g., which way a neutron shoots away), wind it up and watch it go. Since there’s a lot of randomness, let’s run the program a zillion times and average the results.”

Applying this approach to inventory management, we have a different set of randomly occurring events: e.g., a demand of a given size arrives on a random day, a replenishment of a given size arrives after a random lead time, we cut a replenishment PO of a given size when stock drops to or below a given reorder point. We code the logic relating these events into a program. We feed it with a random demand sequence (see bootstrapping above), run the program for a while, say one year of daily operations, compute performance metrics like Fill Rate and Average On Hand inventory, and “toss the dice” by re-running the program many times and averaging the results of many simulated years. The result is a good estimate of what happens when we make key management decisions: “If we set the reorder point at 10 units and the order quantity at 15 units, we can expect to get a service level of 89% and an average on hand of 21 units.” What the simulation is doing for us is exposing the consequences of management decisions based on realistic demand scenarios and solid math. The guesswork is gone.

Figure 2 shows some of the inner workings of a Monte Carlo simulation of an inventory system in four panels. The system uses a Min/Max inventory control policy with Min=10 and Max=25. No backorders are allowed: you have the good or you lose the business. Replenishment lead times are usually 7 days but sometimes 14. This simulation ran for one year.

The first panel shows a complex random demand scenario in which there is no demand on weekends, but demand generally increases each day from Monday to Friday. The second panel shows the random number of units on hand, which ebbs and flows with each replenishment cycle. The third panel shows the random sizes and timings of replenishment orders coming in from the supplier. The final panel shows the unsatisfied demand that jeopardizes customer relationships. This kind of detail can be very useful for building insight into the dynamics of an inventory system.

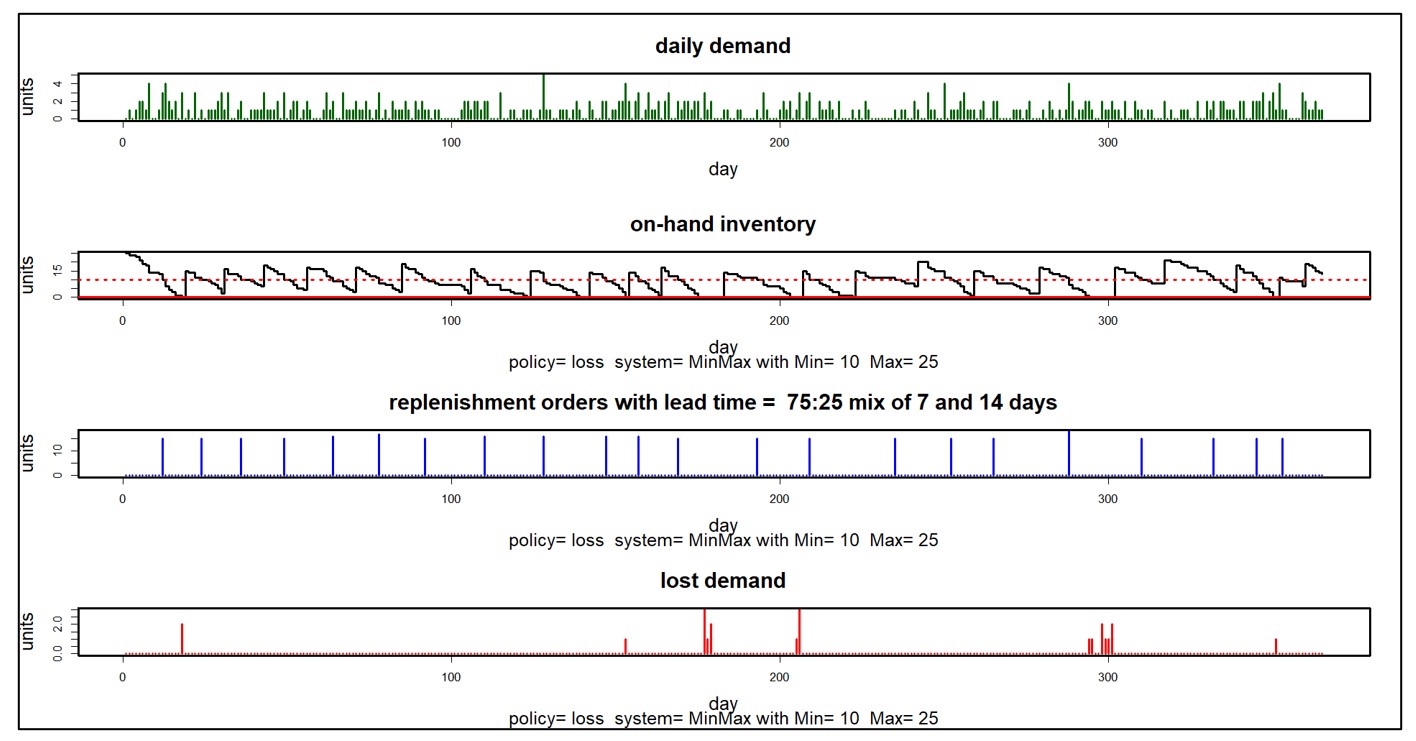
Figure 2: Details of a Monte Carlo simulation

Figure 2 shows only one of the countless ways that the year could play out. Generally, we want to average the results of many simulated years. After all, nobody would flip a coin once to decide if it were a fair coin. Figure 3 shows how four key performance metrics (KPI’s) vary from year to year for this system. Some metrics are relatively stable across simulations (Fill Rate), but others show more relative variability (Operating Cost= Holding Cost + Ordering Cost + Shortage Cost). Eyeballing the plots, we can estimate that the choices of Min=10, Max=25 leads to an average Operating cost of around $3,000 per year, a Fill Rate of around 90%, a Service Level of around 75%, and an Average On Hand of about 10

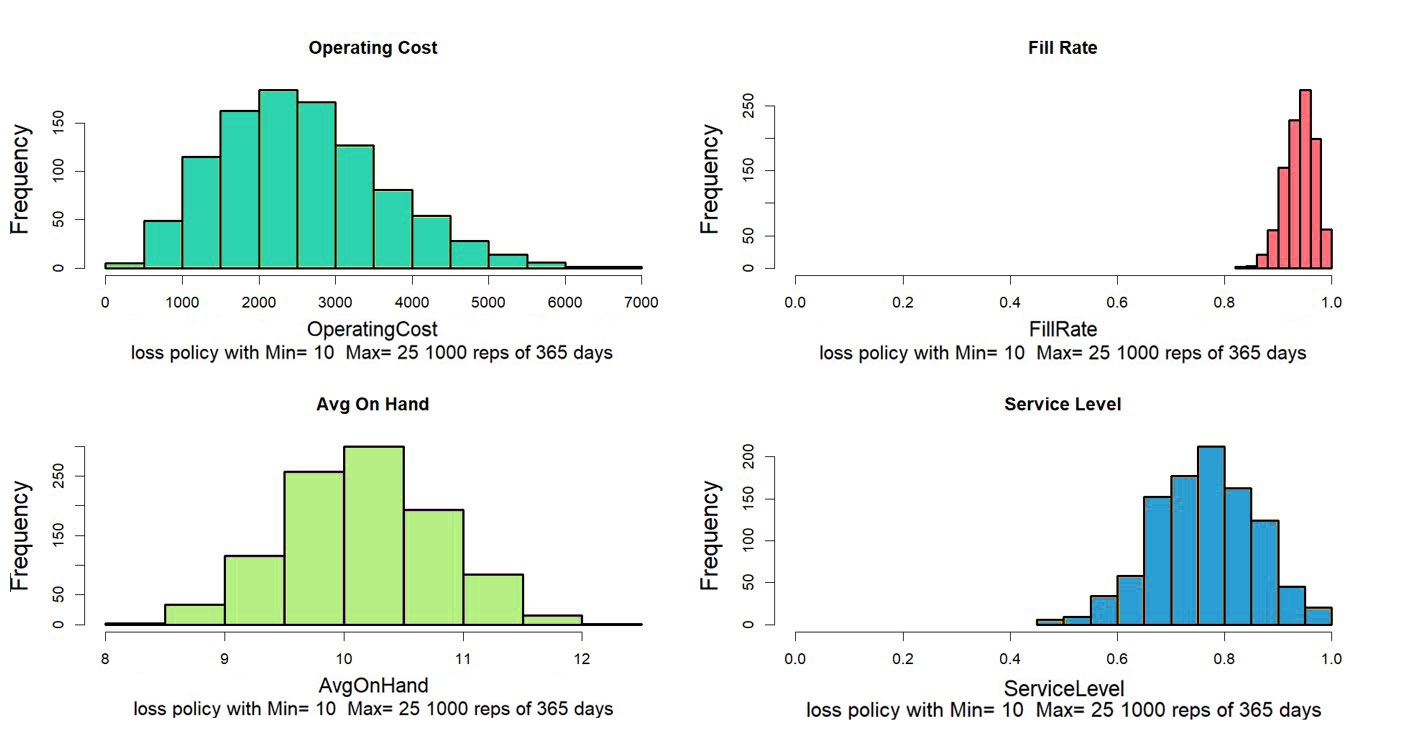
Figure 3: Variation in KPI’s computed over 1,000 simulated years

In fact, it is now possible to answer a higher level of management question. We can go beyond “What will happen if I do such-and-such?” to “What is the best thing I can do to achieve a fill rate of at least 90% for this item at the lowest possible cost?” The mathemagic  behind this leap is yet another key technology called “stochastic optimization”, but we’ll stop here for now. Suffice it to say that Smart’s SIO&P software can search the “design space” of Min and Max values to automatically find the best choice.

1. Forecasting is an art that requires a mix of professional judgment and objective statistical analysis. Successful demand forecasts require a baseline prediction leveraging statistical forecasting methods. Once established, the process can focus on how best to adjust statistical forecasts based on your own insights and business knowledge.

2. The forecasting process is usually iterative. You may need to make several refinements of your initial forecast before you are satisfied. It is important to be able to generate and compare alternative forecasts quickly and easily. Tracking accuracy of these forecasts over time, including alternatives that were not used, helps inform and improve the process.

3. The credibility of forecasts depends heavily on graphical comparisons with historical data.  A picture is worth a thousand words, so always display forecasts via instantly available graphical displays with supporting numerical reports.

4. One of the major technical tasks in forecasting is to match the choice of forecasting technique to the nature of the data. Effective demand forecasting processes employ capabilities that identify the right method to use.  Features of a data series like trend, seasonality or abrupt shifts in level suggest certain techniques instead of others. An automatic selection, which selects and uses the appropriate forecasting method automatically, saves time and ensures your baseline forecast is as accurate as possible.

5. Successful demand forecasting processes work in tandem with other business processes.   For example, forecasting can be an essential first step in financial analysis.  In addition, accurate sales and product demand forecasts are fundamental inputs to a manufacturing company’s production planning and inventory control processes.

6. A good planning process recognizes that forecasts are never exactly correct. Because some error creeps into even the best forecasting process, one of the most useful supplements to a forecast are honest estimates of its margin of error and forecast bias.

What’s all the hoopla around the term “probabilistic forecasting?” Is it just a more recent marketing term some software vendors and consultants have coined to feign innovation? Is there any real tangible difference compared to predecessor “best fit” techniques?  Aren’t all forecasts probabilistic anyway?

To answer this question, it is helpful to think about what the forecast really is telling you in terms of probabilities.  A “good” forecast should be unbiased and therefore yield a 50/50 probability being higher or lower than the actual.  A “bad” forecast will build in subjective buffers (or artificially depress the forecast) and result in demand that is either biased high or low.  Consider a salesperson that intentionally reduces their forecast by not reporting sales they expect to close to be “conservative.” Their forecasts will have negative forecast bias as actuals will nearly always be higher than what they predicted.   On the other hand, consider a customer that provides an inflated forecast to their manufacturer.  Worried about stockouts, they overestimate demand to ensure their supply.  Their forecast will have a positive bias as actuals will nearly always be lower than what they predicted. 

These types of one-number forecasts described above are problematic.  We refer to these predictions as “point forecasts” since they represent one point (or a series of points over time) on a plot of what might happen in the future.   They don’t provide a complete picture because to make effective business decisions such as determining how much inventory to stock or the number of employees to be available to support demand requires detailed information on how much lower or higher the actual will be!  In other words, you need the probabilities for each possible outcome that might occur.  So, by itself, the point forecast isn’t probabilistic one.   

To get a probabilistic forecast, you need to know the distribution of possible demands around that forecast.  Once you compute this, the forecast becomes “probabilistic.”  How forecasting systems and practitioners such as demand planners, inventory analysts, material managers, and CFOs determine these probabilities is the heart of the question: “what makes a forecast probabilistic?”     

Normal Distributions
Most forecasts and the systems/software that produce them start with a prediction of demand.  Then they figure out the range of possible demands around that forecast by making incorrect theoretical assumptions about the distribution.  If you’ve ever used a “confidence interval” in your forecasting software, this is based on a probability distribution around the forecast.  The way this range of demand is determined is to assume a particular type of distribution.  Most often this means assuming a bell shaped, otherwise known as a normal distribution.  When demand is intermittent, some inventory optimization and demand forecasting systems may assume the demand is Poisson shaped. 

After creating the forecast, the assumed distribution is slapped around the demand forecast and you then have your estimate of probabilities for every possible demand – i.e., a “probabilistic forecast.”  These estimates of demand and associated probabilities can then be used to determine extreme values or anything in between if desired.  The extreme values at the upper percentiles of the distribution (i.e., 92%, 95%, 99%, etc.) are most often used as inputs to inventory control models.  For example, reorder points for critical spare parts in an electrical utility might be planned based on a 99.5% service level or even higher.  While a non-critical service part might be planned at an 85% or 90% service level.

The problem with making assumptions about the distribution is that you’ll get these probabilities wrong.  For example, if the demand isn’t normally distributed but you are forcing a bell shaped/normal curve on the forecast then how can then the probabilities will be incorrect.  Specifically, you might want to know the level of inventory needed to achieve a 99% probability of not running out of stock and the normal distribution will tell you to stock 200 units.  But when compared to the actual demand, you come to find out that 200 units only filled demand entirely in 40/50 observations.  So, instead of getting a 99% service level you only achieved an 80% service level!  This is a gigantic miss resulting from trying to fit a square peg into a round hole.  The miss would have led you to take an incorrect inventory reduction.

Empirically Estimated Distributions are Smart
To produce a smart (read accurate) probabilistic forecast you need to first estimate the distribution of demand empirically without any naïve assumptions about the shape of the distribution.  Smart Software does this by running tens of thousands of simulated demand and lead time scenarios.  Our solution leverages patented techniques that incorporate Monte Carlo simulation, Statistical Bootstrapping, and other methods.  The scenarios are designed to simulate real life uncertainty and randomness of both demand and lead times.  Actual historical observations are utilized as the primary inputs, but the solution will give you the option of simulating from non-observed values as well.  For example, just because 100 units was the peak historical demand, that doesn’t mean you are guaranteed to peak out at 100 in the future.  After the scenarios are done you will know the exact probability for each outcome. The “point” forecast then becomes the center of that distribution.  Each future period over time is expressed in terms of the probability distribution associated with that period.

Leaders in Probabilistic Forecasting
Smart Software, Inc. was the first company to ever introduce statistical bootstrapping as part of a commercially available demand forecasting software system twenty years ago.  We were awarded a US patent at the time for it and named a finalist in the APICS Corporate Awards of Excellence for Technological Innovation.  Our NSF Sponsored research that led to this and other discoveries were instrumental in advancing forecasting and inventory optimization.    We are committed to ongoing innovation, and you can find further information about our most recent patent here.

Many companies looking to improve their forecasting process don’t know where to start. It can be confusing to contend with learning new statistical methods, making sure data is properly structured and updated, agreeing on who “owns” the forecast, defining what ownership means, and measuring accuracy. Having seen this over forty-plus years of practice, we wrote this blog to outline the core focus and to encourage you to keep it simple early on.

1. Objectivity. First, understand and communicate that the Demand Planning and Forecasting process is an exercise in objectivity. The focus is on getting inputs from various sources (stakeholders, customers, functional managers, databases, suppliers, etc.) and deciding whether those inputs add value. For example, if you override a statistical forecast and add 20% to the projection, you should not just assume that you automatically got it right. Instead, be objective and check whether that override increased or decreased forecast accuracy. If you find that your overrides made things worse, you’ve gained something: This informs the process and you know to better scrutinize override decisions in the future.

2.  Teamwork. Recognize that forecasting and demand planning are team sports. Agree on who will captain the team. The captain is responsible for creating the baseline statistical forecasts and supervising the demand planning process. But results depend on everyone on the team making positive contributions, providing data, suggesting alternative methodologies, questioning assumptions, and executing recommended actions. The final results are owned by the company and every single stakeholder.

3. Measurement. Don’t fixate on industry forecast accuracy benchmarks. Every SKU has its own level of “forecastability”, and you may be managing any number of difficult items. Instead, create your own benchmarks based on a sequence of increasingly advanced forecasting methods. Advanced statistical forecasts may seem dauntingly complex at first, so start simple with a basic method, such as forecasting the historical average demand. Then measure how close that simple forecast comes to the actual observed demand. Work up from there to techniques that deal with complications like trend and seasonality. Measure progress using accuracy metrics calculated by your software, such as the mean absolute percentage error (MAPE). This will allow your company to get a little bit better each forecast cycle.

4. Tempo. Then focus efforts on making forecasting a standalone process that isn’t combined with the complex process of inventory optimization. Inventory management is built on a foundation of sound demand forecasting, but it is focused on other topics: what to purchase, when to purchase, minimum order quantities, safety stocks, inventory levels, supplier lead times, etc. Let inventory management go to later. First build up “forecasting muscle” by creating, reviewing, and evolving the forecasting process to have a regular cadence. When your process is sufficiently matured, catch up with the increasing speed of business by increasing the tempo of your forecasting process to at least a monthly cadence.

Remarks

Revising a company’s forecasting process can be a major step. Sometimes it happens when there is executive turnover, sometimes when there is a new ERP system, sometimes when there is new forecasting software. Whatever the precipitating event, this change is an opportunity to rethink and refine whatever process you had before. But trying to eat the whole elephant in one go is a mistake. In this blog, we’ve outlined some discrete steps you can take to make for a successful evolution to a better forecasting process.